一种适应于IEEE 802.15.4k标准的高精度频偏估计算法*
叶晓青 罗炬锋 邱云周 朱元萍 黄河笑
(1.中国科学院上海微系统与信息技术研究所,上海,200050;2.上海物联网有限公司,上海,201899;3.上海开放大学理工学院,上海,200433)
引 言
IEEE 802.15.4k[1]标准面向低成本、远距离和关键基础设施监控网络(Low energy critical infrastructure monitoring,LECIM)设计,其物理层支撑直接序列扩频(Direct sequency spread spectrum,DSSS)通信和频移键控(Frequency-shift keying,FSK)通信,其中DSSS具有发射功率低、抗干扰性强等优点,常用于低信噪比应用环境[2]。实际数字通信中,晶振的频率漂移将引起接收性能恶化,而噪声的干扰会极大地影响接收端频偏估计的精度,因此如何在极低信噪比环境下实现频偏估计是无线通信系统中的关键技术。
IEEE 802.15.4k标准定义2或4字节的前导码(Preamble)用于同步[3],接收机利用已知的前导码来完成捕获和数据辅助的频偏估计。基于数据辅助[4]的载波频偏估计方法主要分为时域和频域两大类,而基于时域的频偏估计方法又分为基于信号差分的相位和基于自相关函数的相位两类,前者有经典的Kay和L&R算法[5-6],后者有Fitz和M&M等[7-8],其中M&M基于自相关序列的辐角差分估计频偏,估计范围广但信噪比门限较高,文献[9]也从自相关辐角估计的角度提出相应的算法。文献[10]也给出了一种基于自相关函数加权平均的方法,可扩展估量范围但无法降低信噪比门限。基于频域的频偏估计方法主要借助于快速傅里叶变换(Fast Fourier transformation,FFT)[11]。在FFT基础上进行二次插值可以提高其精度,但仅适用于特定的频偏,无法满足随机频偏下的估计精度要求[12],文献[13]针对超高速的移动宽带中的Doppler频移提出了相应的频率偏移的计算方法。Hasebe等[14]借助奇异值分解(Singular value decomposition,SVD)和自适应滤波的迭代方法可实现超大范围的频偏估计,但信噪比门限较高,均不能满足IEEE 802.15.4k标准下长码字扩频中低信噪比和估计精度的整体需求。
为实现极低信噪比环境下的准确频偏估计,本文给出了一种改进的结合Fitz和提升信噪比的方法。Fitz算法是一种近似的最大似然(Maximum likelihood,ML)算法,实现简单,但一方面其频偏估计的范围随相关阶数M的增大而减小,而估计精度随着M的增大而提高,两者存在矛盾,另一方面其近似的成立条件是噪声不能太大,当信噪比足够低时无法正确估计。针对Fitz算法存在的第1个问题,已有学者进行了相关的研究。因此本文主要解决Fitz算法在信噪比极低时如何继续保证估算精度的问题。由于Fitz算法对自相关序列加权后运行近似方法获得相位,当信噪比低时受噪声影响大,近似条件不满足。因此本文对消除伪码信息后的序列先做有偏自相关,结合其幅度信息来提高携带相位信息序列的信噪比,然后基于加权的相关函数的辐角进行高精度的频偏估计,能适应于IEEE802.15.4k标准下的长码字通信应用场景。
1 信号模型与经典Fitz算法分析
IEEE 802.15.4k标准面向低成本、远距离通信,在低信噪比环境下工作,系统建模如下:物理层采用DSSS通信方式,采用长码字扩频,在高斯信道中传输,接收端带有载波频偏的复采样信号可以表示为
s(k)=a(k)ej(2πΔfTk+θ)+n(k)
(1)
式中:a(k)为第k个伪码信息,Δf对应载波频偏,T为码片周期,θ为本地相位,n(k)对应于均值是零,方差是σ2的复高斯白噪声项。
得到码片同步信息之后,将s(k)与前导码中对应的码字共轭相乘,消除伪码信息的影响,即
t(k)=a(k)×a*(k)×ej(2πΔfTk+θ)+a*(k)n(k)=|a(k)|2×ej(2πΔfTk+θ)+a*(k)n(k)=x(k)+n(k)
(2)
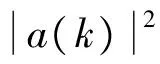
经典Fitz法是对最大似然估计方法的近似,它基于自相关函数,计算不同阶次相关函数的辐角并赋予不同的权重,即
(3)
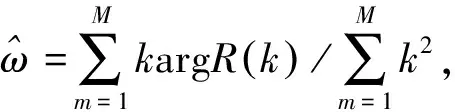
2 基于有偏自相关的频偏估计算法
针对低信噪比环境下自相关函数受噪声的影响非常大,无法估计出频偏的问题,本文提出了一种增强处理方法。普通晶振的稳定度在10~20 PPM左右,则收发频差为20~40 PPM,对应的频偏范围限定了M的选取,因此本文并不增加阶数M,而是将幅度的信息和相位的信息结合,在保证频偏估计范围的前提下,进行迭代有偏自相关增强处理,以保证其在极低信噪比下的精度。
本文先对接收端的采样信号作有偏自相关增强处理,然后进行迭代,不仅利用了其相位信息,还利用了其幅度信息。先对信号求有偏相关并结合式(2),得到
k=1,2,…,N-1
(4)
式中:N为数据点数,且有N≫M;有偏相关操作相当于对携带频偏信息的有用信号的每一项进行幅值上的加权,而相位所包含的频偏信息不变。若分别考虑信号和噪声部分,式(4)可表示成
Rb(k)=R1(k)+R2(k)+R3(k)+R4(k)
(5)
式中
(6)
第1项对应携带频偏信息的有用信号部分,即
(7)
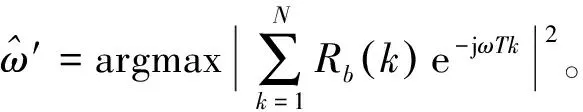
(8)

(9)
式中:M取值由最大频偏范围决定,满足Δf<π/MT[8]且有M≪N。
3 抗噪声性能分析
有偏自相关操作相当于对有用信号的幅值进行加权,而相位信息不变,可以大大改善信噪比。分析式(6),由于噪声满足均值为0,容易得到R2,R3和R4的均值均为0。第2项对应于信号和噪声相乘,其方差为
(10)
由高斯白噪声的性质可知,式(10)只在m=i时不为0,又由于均值为0,故可得出对应方差为[15]
(11)
(12)
由文献[16]可知,零均值的复高斯信号满足
(13)
从而将式(13)化简为
(14)
式(14)只在m=i时不为0,因此噪声复乘项的方差为
(15)
由文献[8]可知,未处理的信噪比为SNRi=1/σ2。而处理后的信号平均功率为
(16)
处理后噪声的平均功率可表示为
(17)
其中存在的交叉项为
故可将式(17)简化为
(18)
对应处理后的信噪比为
(19)
若转化为dB形式,对式(19)两边取对数,则有
(20)
当信噪比为正时,只要N大于1则必然有SNRo(dB)>SNRi(dB)。当信噪比较小(为负)时,SNRo与SNRi的大小与N长度有关,记N=2i,图1给出了仿真结果。如图1所示,低信噪比情况下,处理后信噪比(SNRo)曲线与处理前信噪比(SNRi)曲线在不同N时有一系列的交点。交点的含义是输入信噪比与预处理输出信噪比相等,在交点左边代表预处理恶化性能,在交点右边代表预处理提高了信噪比。从图1中可以看出针对IEEE 802.15.4k标准的长码字应用,本算法适用的信噪比非常低,满足系统接收灵敏度指标。参考IEEE 802.15.4k标准,设置伪码长度为1 024,发送端采用(2,1,7)卷积码和O-QPSK调制,基带系统工作的最低信噪比理论上约为-24dB@BER10-5,而本算法的适用范围为大于-28 dB,因此完全满足该工作环境。
经过该处理后,有用的相位信息得以保存而噪声项削减。在其基础上进行扩展,即进行有偏相关操作的迭代,可以进一步抑制噪声干扰,减小估计误差。
4 仿真分析
分析基于IEEE802.15.4k的DSSS系统中长码字扩频在低信噪比环境下的估计性能,仿真参数如下:采用1 024码长的m序列,载波频率780 MHz,普通晶振稳定度为10 PPM,则实际的收发频差是20 PPM内的随机数,发送端经过(2,1,7)卷积编码,码片速率400 kc/s。每个信噪比仿真帧数为10 000。采取归一化的均方误差(NMSE)[17]来对比几种方法的估计性能。本文主要进行了4部分的仿真与测试。
(1)比较算法在不同信噪比条件中的估计误差。Fitz算法的频偏估计范围与相关阶数M有关,为[-1/2MT,-1/2MT][8],其中T为采样周期。根据仿真参数可推出M应小于12.8,仿真中M设置为10,前导码利用的信息比特数为8,仿真结果如图2所示。其中I对应经典的Fitz法,当其处于高信噪比(>-10 dB)时精度较高(图中未画出),但随着信噪比越来越低,已经几乎无法正常工作。II对应文献[10]的算法,与Fitz类似,低信噪比时估计偏差大。III对应本文提出的通过有偏自相关增强处理的改进算法,III与I相比,有较明显的改善作用,但在更低信噪比下,估算精度未能达到IEEE 802.15.4k标准的要求。IV对应本文的扩展算法,即在III的基础上迭代1次,其在低信噪比下的估算精度有显著的提高。V对应扩展方法中迭代的次数取2,VI对应扩展方法中迭代3次。比较可知,当迭代次数取2和3时效果改善已经不明显, 迭代2次即已满足要求, 在信噪比大于-28 dB环境中的估算精度接近克拉美劳下限[17]。
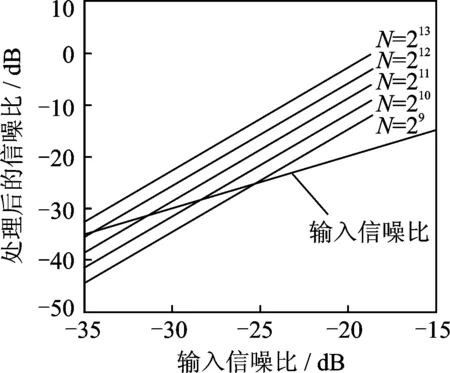
图1 不同N长度下处理前后信噪比的对比Fig.1 Comparison of SNR before and after treatment with different N
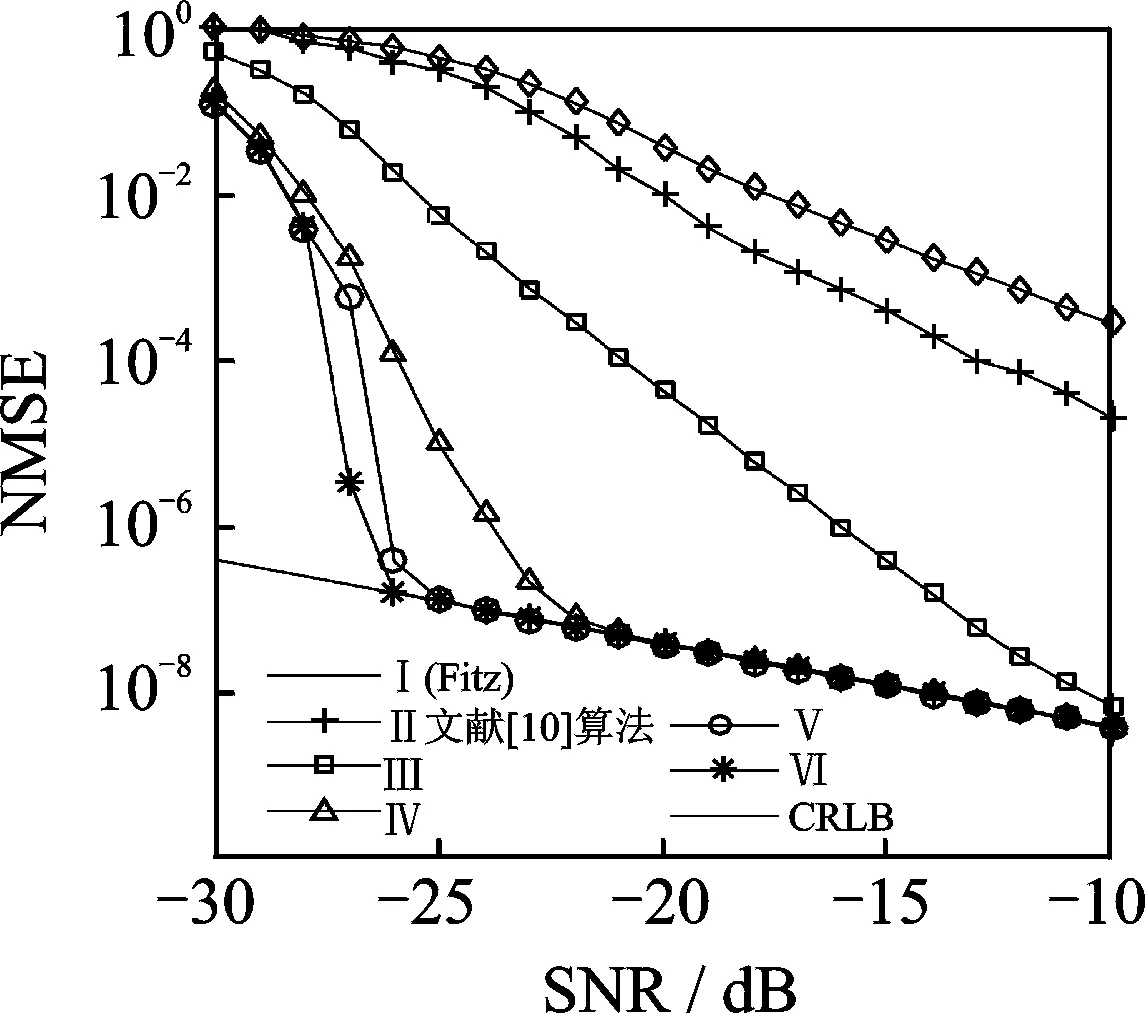
图2 不同信噪比条件下的归一化估计方差Fig.2 Normalized estimation variance under different SNRs
(2) 仿真通过比较理论推导结果与实际测试结果的对比来验证第3部分中分析的正确性。借助求解实际信号的信噪比并与理论分析结果比较,如图3所示,其中N=212,213。由图3可见,其理论值和实际测试结果的吻合度较高,说明理论的分析在一定程度上可靠。
(3)比较不同相关阶数下估计的精度差异。Fitz算法的性能与最大延迟长度M有关,不同M取值下算法估计的性能仿真结果如图4所示。其中I对应经典Fitz放法,增大M对较高信噪比环境下的估计性能有一定的改善作用,当信噪比较低时,基本没有改善。II对应本文的改进方法,III对应扩展方法,仿真中迭代取1次。由图4的仿真结果可以看出,在不超过最大允许延迟长度的前提下,增大M一定程度上可以改善性能,但同时看到随着迭代次数的增加,增大M改善性能的幅度已经不大。

图3 理论和实际信噪比对比Fig.3 Comparison between theoretical and practical SNR
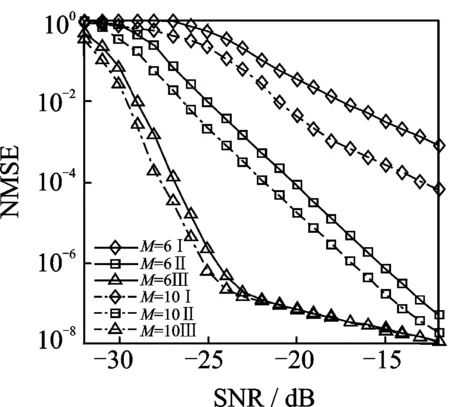
图4 不同M长度情况下的归一化估计方差Fig.4 Normalized estimation variance under different M
(4)测试改进算法的估计误差范围。当扩频因子为1 024,码片速率Rc=1/Tc=400 kc/s时,根据IEEE 802.15.4k标准,若要保证无误码情况,数据在一个比特内相位旋转不应超过π/4,则残余频偏不能超过48 Hz。为评估本文方法在低信噪比时的误差分布范围,在信噪比均为-27 dB时,令频率偏移分别等于1,10和20 PPM并各仿真10 000次得到估计误差的直方图如图5所示。
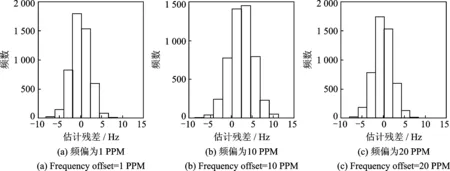
图5 不同频偏条件下估计残余偏差分布直方图Fig.5 Histogram of residual estimation error under different frequency offsets
当信噪比为-27 dB且预置频偏在1,10和40 PPM时,估计残余偏差均在[-15,15]Hz范围内,此时不会引起误码,满足IEEE 802.15.4k中长码字扩频系统对残余频偏的容忍度。
5 结束语
为解决长码字直接序列扩频在极低信噪比中的频偏估计问题,在不增加自相关阶数的前提下,本文提出了一种增强处理方法。该算法通过有偏自相关并迭代的方法抑制噪声,同时结合其相位信息和幅度信息,在保证频偏信息不受影响的同时提升信噪比,使Fitz算法的近似条件得以成立,具有一定的适用性,可应用于借助自相关函数进行频偏估算的同类算法。本方法实现了低信噪比环境下的稳定、高精度的频偏估计,适合于IEEE802.15.4k标准下超长码字、超低信噪比和远距离通信应用领域。
[1] LAN/MAN Standards Committee. IEEE 802.15.4k-2013. Part 15.4: Physical layer specifications for low energy, critical infrastructure monitoring networks[S]. New York, USA: The Institute of Electrical and Electronics Engineers, Inc., 2013:1-149.
[2] Dai Shenchen, Qian Hua, Kang Kai, et al. A robust demodulator for OQPSK-DSSS system [J]. Circuits, Systems, and Signal Processing, 2015, 34(1): 231-247.
[3] Ith V, Baykas T, Kato S. Improving preamble detection performance of IEEE P802.15.4 k DSSS PHY[C]//2013 IEEE 24th International Symposium on Personal Indoor and Mobile Radio Communications (PIMRC).London:IEEE,2013:63-67.
[4] Xin Dingxin, He Jin, Chen Lin, et al. Data-aided channel estimation and frequency domain equalization of minimum-shift keying in optical transmission systems[J]. Chinese Optics Letters, 2014, 12(4): 34-38.
[5] Kay S. A fast and accurate single frequency estimator [J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1989, 37(12): 1987-1990.
[6] Luise M, Reggiannini R. Carrier frequency recovery in all-digital modems for burst-mode transmissions [J]. IEEE Transactions on Communications, 1995, 43(2/3/4): 1169-1178.
[7] Umberto M, Morelli M .Data-aided frequency estimation for burst digital transmission [J]. IEEE Transactions on Communications, 1997, 45(1): 23-25.
[8] FITZ M P. Further results in the fast frequency estimation of a single frequency [J]. IEEE Transactions on Communications, 1994, 42(3): 862-864.
[9] 方绍峡,金德鹏,苏厉,等. 基于线性回归的UWB系统频偏估计算法[J]. 数据采集与处理,2012,27(1):101-104.
Fang Shaoxia, Jin Depeng, Su Li, et al. Novel frequency offset estimation algorithm based on liner regression in UWB system[J]. Journal of Data Acquisition and Processing, 2012, 27(1): 101-104.
[10] 周磊磊, 罗炬锋, 付耀先, 等. 低信噪比下基于自相关函数的频率估计方法[J]. 华中科技大学学报:自然科学版, 2014, 42(4): 45-49.
Zhou Leilei, Luo Jufeng, Fu Yaoxian, et al. Frequency estimator based on autocorrelation with low SNR [J]. Journal of Huazhong University of Science and Technology:Natural Science Edition, 2014, 42(4): 45-49.
[11] Xiao Junxiong, Feng Jie, Han Jilong, et al. Low complexity FFT-based frequency offset estimation for M-QAM coherent optical systems [J]. IEEE Photonics Technology Letters, 2015, 27(13): 1371-1374.
[12] Wang Shuai, Shao Jun, Tu Shuiping, et al. Carrier frequency offset estimation for DSSS signals in the wired test of beamforming networks [C]//TENCON 2015-IEEE Region 10 Conference. Macau, China:IEEE, 2015: 1-6.
[13] 丁志中,王定良,傅银玲,等. 超高速移动空-空宽带通信网及其物理层关键技术[J].数据采集与处理,2015,30(4): 725-732.
Ding Zhizhong, Wang Dingliang, Fu Yinling, et al. Air to air wideband network with ultra-high node velocity and its key technology of physical layer [J]. Journal of Data Acquisition and Processing, 2015, 30(4): 725-732.
[14] Hasebe M, Denno S, Tomisato S, et al. Iterative frequency offset estimation based on singular value decomposition [C]//International Symposium on Intelligent Signal Processing and Communications Systems.Naha,Japan: IEEE, 2014: 125-130.
[15] Chowdhary G, Kingravi H, How J P, et al. Bayesian nonparametric adaptive control using Gaussian processes [J]. IEEE Transactions on Neural Networks and Learning Systems, 2015, 26(3): 537-550.
[16] Awoseyila B. Robust synchronization for PSK (DVB-S2) and OFDM systems [M]. London: University of Surrey, 2008: 67-73.
[17] Masjedi M, Hoseini A M D. Data-assisted channel estimation and performance analysis for two-way amplify-and-forward relay networks with M-ary frequency shift keying modulation [J]. IET Communications, 2015, 9(18): 2242-2252.

