应用于特征提取方法的模糊差分嵌入投影*

万鸣华

(1.南京审计大学工学院，南京，211815；2.东南大学信息科学与工程学院，南京，210096)

引 言

目前，众多的特征提取算法在模式识别、机器学习和数据挖掘的研究领域中受到了广泛的关注。在这些特征提取算法中，最为经典的特征提取算法有线性鉴别分析方法(Linear discriminant analysis,LDA)[1]和主成分分析(Principle component analysis,PCA)[2]两种。这两种特征提取算法在各类图像识别中取得了较好的识别效果。PCA和LDA算法所得到的图像特征是线性的特征，因此，它们本质上都是线性的特征提取方法。

为了发现非线性数据中的流形结构，众多学者已经提出了许多流形学习相关算法。目前，流形学习的研究方法有主流形[3]、谱分析[4]、变分法[5]和互信息[6]。当前基于流形学习的特征提取算法有等距离映射(Isometric mapping,ISOMAP)[7]、局部线性嵌入(Locally linear embedding,LLE)[8]和拉普拉斯算子特征映射(Laplacian eigemap,LE)[9]等。

由于样本缺少泛化能力，上述的流形学习以及拓展方法不适合应用在图像识别中。为了解决这个问题，He[10]等人提出了局部保持投影(Locality preserving projections,LPP)方法并将其成功应用于人脸识别。由于LPP算法是无监督的，众多研究者通过增加样本类别信息相继提出了边缘Fisher分析(Marginal fisher analysis,MFA)[11]和局部鉴别嵌入(Local discriminant embedding,LDE)[12]等相关的学习算法[13]。

上述讨论的流形学习以及拓展方法只考虑流形上的邻近点，没有考虑全局流形结构几何特性。即当流形上距离比较远的数据样本点之间的联系较弱或者邻域之间的数据样本点交叠不够的时候，会出现高维空间数据样本点映射错误的情况。同时不同人脸之间在高维空间也存在结构相似的问题，导致识别率降低。解决该问题比较有效的方法有Fuzzy Fisherface[14]方法，但是该方法仅在计算样本类内中心样本时考虑了样本分布信息，并没有充分利用样本分布信息。

针对上述问题，在模糊数学和流形学习的思想指导之下，通过模糊隶属度(Fuzzy sets)[15]和局部线性嵌入[16]表示的形式，将测试数据样本重新划入所在的类别之中，提出一种新的局部与全局保持嵌入 (Fuzzy difference embedding projection,FDEP)算法。FDEP算法用模糊隶属度来表示原始样本的分布信息；其次，利用局部线性嵌入分别构建模糊局部近邻图与模糊全局方差图来表示局部近邻与全局结构信息；最后，通过拉格朗日乘子法解决了FDEP算法约束条件下的优化问题。在ORL,Yale和AR三个标准人脸库上的实验结果验证了FDEP算法的有效性。

1 相关算法

将数据样本集X={x1,x2,…,xN},xi∈Rn从高维特征空间中寻求一个最优的投影矩阵V=[v1,v2,…,vd]映射到一个相对低维的特征空间Rd,d≤n。这样，Y={y1,y2,…,yN},yi=VTxi可以表述为在新特征空间中的数据样本,其中投影矩阵V由d个最佳鉴别矢量vi构成。

1.1 局部线性嵌入(LLE)

LLE算法分为如下3个步骤：

Step1计算数据样本集X中xi的k个邻域点{xi1,xi2,…,xik}，其中k为大于零的常数。

Step2通过定义误差函数式(1)来计算数据样本点的局部重建权重矩阵Wij

(1)

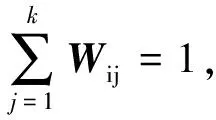
Step3通过最小化式(2)将所有的样本点从高维空间映射到低维空间中。映射条件为

(2)

1.2 模糊K近邻方法

设U=[Uij]为模糊隶属度矩阵，其中i=1,2,…,c，j=1,2,…,N，矩阵U中的元素Uij表示第j个训练样本对于第i类的依赖程度，并且Uij必须满足式(3，4)的两个条件。

(3)

(4)

可以通过下面3个步骤得到矩阵Uij。

Step1构成一个N×N的距离矩阵。通过计算训练数据样本集X={x1,x2,…,xN},xi∈Rn为任意两个数xi和xj距样本点之间的欧氏距离。

Step2将步骤1中得到的N×N距离矩阵的对角线上的元素置为无穷大，并将距离矩阵的每一列或者每一行按照距离值从小到大排列。

Step3隶属度矩阵计算。根据式(5)计算第j个样本跟第i类的隶属度。

(5)

式中nij表示第j个样本的k个最近邻数据样本点中属于第i类的数据样本个数。

2 模糊的嵌入差分投影

由于PCA算法是一种基于全局结构信息的方法,不能发现数据样本点的局部结构信息。而LLE算法是通过邻域内其他数据样本点的线性表示，不能发现高维数据样本点的全局结构信息。因此，本文利用PCA和LLE的优势，结合模糊隶属度，分别构造模糊全局方差图与模糊局部近邻图来表示全局与局部近邻结构信息。约束条件下FDEP目标函数的优化问题通过拉格朗日乘子法来解决。FDEP目标函数主要通过以下3个方面来实现。

2.1 模糊局部最小嵌入

模糊局部最小嵌入算法可分为4步来描述，具体如下：

Step1计算每个测试样本数据点xi的k个距离最近的点集合{xi1,xi2,…,xik}；

Step2通过最小重构误差式(6)计算重建每个数据样本点xi的权值W=[wij]N×N。

(6)

式(6)的最小重构误差可以化简如下

(7)

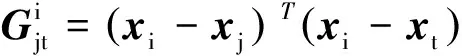
(8)

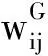
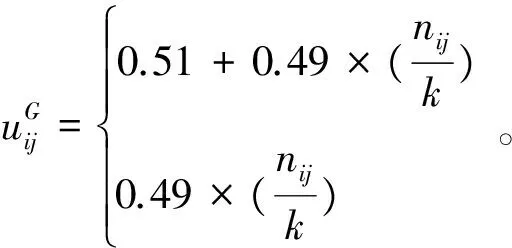
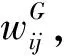
(9)

最后，式(9)最小重构函数通过一个线性变换Y=VTX化简如下

tr{Y(I-WG)T(I-WG)YT}=tr{VTXMXTV}

(10)

式中M=(I-WG)T(I-WG)。

2.2 模糊全局最大方差

数据样本最大全局散度的目标函数为

(11)

通过一个线性变换Y=VTX，式(10) 最大全局散度目标函数可以化简如下

(12)

2.3 FDEP准则

通过同时满足2.1中的最小模糊局部散度JL(W)和2.2中的最大模糊全局散度JG(V)可以找到一个最优的投影方向V，因此可以采用JL(W)，JG(V)和约束条件来解决最优问题

(13)

s.t.VTXDXTV=I

由式(13)可以看到，FDEP算法不仅能最大化非近邻样本点之间的距离，也能保持近邻数据样本点之间内在联系。为了避免类似LDA 中出现的小样本问题，式(13)可以转化成以下形式

min tr{VT((1-α)XMXT-αST)V}

(14)

s.t.VTXDXTV=I

式中α(0≤α<1)为平衡参数，可以利用Lagrange乘数法来解决式(14)最小化问题，即

(15)

[(1-α)XMXT-αST]vi=λiXDXTvi

(16)

式中λi和vi分别为X(M-μLp)XT和XXT的特征值及其对应的特征向量。所以，VULDP=[v1,v2,…,vd]由式(13)的特征方程分解的前d个最小特征向量组成。

3 不同算法的相关性分析

通过对FDEP算法推导，可以看出FDEP算法形式上与LLE和NPE算法非常相似，但是又明显不同。下面分别讨论LLE，NPE和FDEP算法之间的相关性。

3.1 LLE和NPE算法相关性分析

NPE算法是LLE算法的线性化。LLE算法对于新的测试数据样本集不能合适地嵌入，这是由于LLE算法仅仅定义在训练数据样本集上。相反,NPE算法则定义在训练数据样本集和测试数据样本集上。

在LLE算法中,矩阵XMXT是半正定化和对称的，如下所示

YYT=I⟹VTXXTV=I

(17)

最优投影矩阵V可以简化式(18)得到。

(18)

即求解式(19)的广义特征方程前d个最小的特征值所对应的特征向量可以得到投影矩阵V。

XMXTV=λiXXTV

(19)

3.2 NPE和FDEP算法相关性分析

FEDP算法同时保持全局方差和局部近邻嵌入。因此，总体散度矩阵ST也可以写成如下形式

(20)

FEDP算法也可以写成如下带有约束最小化的问题

(21)

因此有

(22)

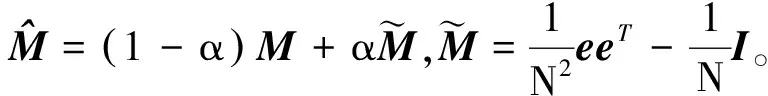
3.3 LLE,NPE和FDEP算法相关性分析

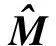
4 实 验

为了验证所提的FDEP算法与PCA、LDA、LLE和MMC等算法的分类识别性能，分别在ORL,Yale和AR标准人脸图像库上进行实验。所有算法均采用欧氏距离来度量和最近邻分类器进行分类，用PCA算法做预处理，并保持约98%的图像能量。实验环境：HP PC，CPU为Inter Athlon(tm) 64 Processor，内存2 GB，Matlab 7.01b。

4.1 实验设计

(1) ORL标准人脸库(http://www.uk.research.att.com/facedatabase.html)总共有400张人脸， 分别由40人构成，每人有10幅图像，大小为56×46灰度。图1是ORL标准人脸库中其中一个人的10幅图像。

图1 ORL标准人脸库中一个人的十张图Fig.1 Ten sample images of one person on the ORL face database

在ORL实验中随机选取l(l=2,3,4,5,6)幅人脸图像做为训练集，剩余(10-l)幅人脸图像做为测试集。每次实验都运行50次，最后的识别结果是50次的平均识别结果。

(2) Yale标准人脸图像库(http://www.cvc.yale.edu/projects/ yalefaces/yalefaces.html)总共包含165幅灰度人脸图像，由15个人构成，每个人又包含11幅人脸图像。这些人脸照片含有不同的表情变化和光照变化。在Yale实验中，图像被处理成50×40灰度的形式。图2显示Yale标准人脸图像库中其中一个人的11幅图像。

图2 Yale 标准人脸库一个人的11张图Fig.2 Eleven sample images of one person on the Yale face database

在Yale实验中随机选取l(l=2,3,4,5,6) 幅人脸图像做为训练集，剩余(11-l)幅人脸图像做为测试集。对于每次选取l图像运行50次实验，最后的识别结果是50次的平均识别结果。

(3) AR标准人脸图像库(http://cobweb.ecn.purdue.edu/～aleix/aleix_face_DB.html) 总共包含4 000多张彩色人脸图像，由126个人(70位男性，56位女性)构成，这些人脸图像在不同的光照、表情和遮挡情况下进行拍摄。在本次实验中采用2 400幅人脸图像，图像被处理成50×40灰度的形式。这些图像包含120个人(没戴围巾的)的人脸图像，其中每人又包含20幅人脸图像。图3是AR标准人脸图像库中一个子类的20 幅图像。

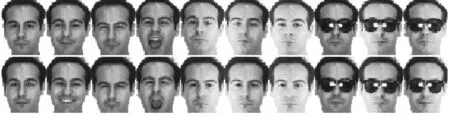
图3 AR人脸图像库中一个子类的20 幅图像Fig.3 Images of one subject of the AR database

在AR实验中随机选取l(l=2,3,4,5,6)幅人脸图像做为训练集，剩余(20-l)幅人脸图像做为测试集。对于每次选取l图像运行10次实验，最后的识别结果是10次实验的平均识别结果。

4.2 实验结果

表1～3为5种算法在ORL，Yale和AR人脸库上的最大平均识别率及其对应的每个类所用训练样本数目(括号内的数字代表最大平均识别率所对应的特征向量维数)。

表15种算法在ORL标准人脸库上的最大平均识别结果及偏差

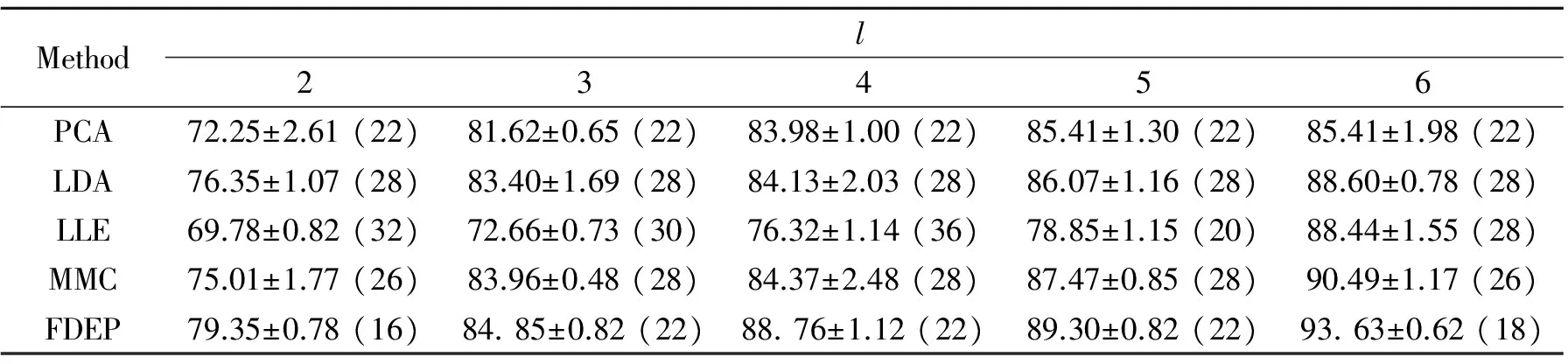
Tab.1 The max average recognition accuracy of five algorithms on the ORL face database and the corresponding standard deviations and dimensions %

表25种算法在Yale人脸库上的最大平均识别结果及偏差

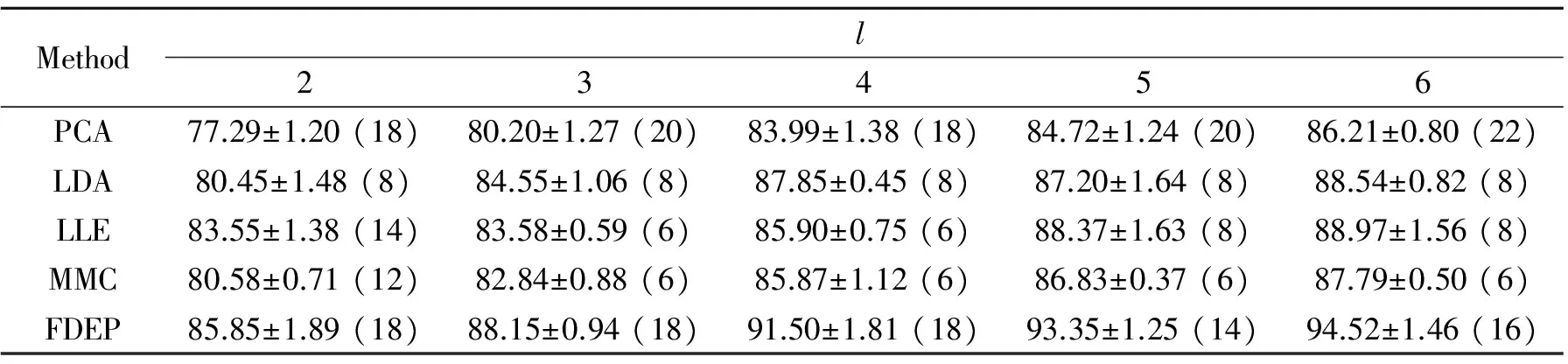
Tab.2 The max average recognition accuracy of five algorithms on the Yale face database and the corresponding standard deviations and dimensions %

表35种算法在AR人脸库上的最大平均识别结果及偏差

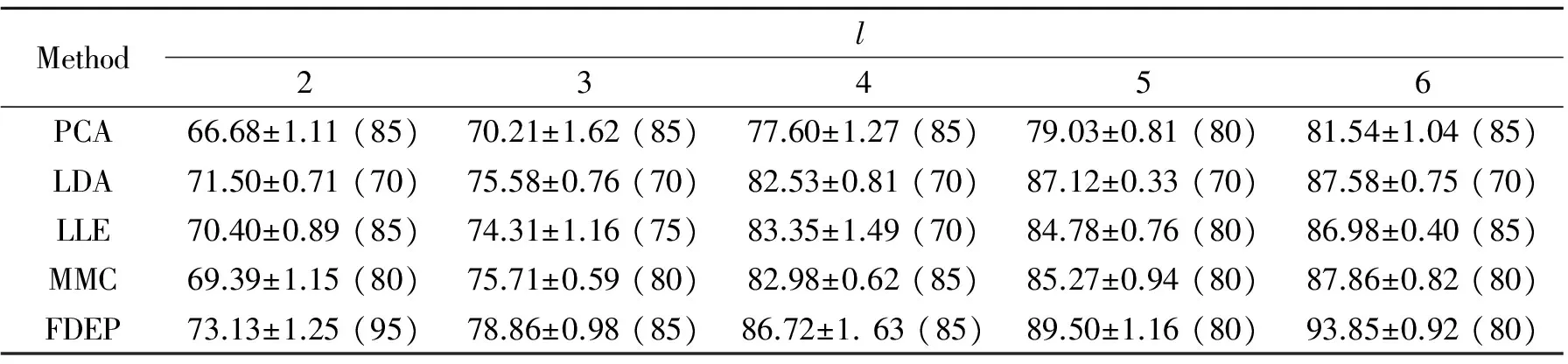
Tab.3 The max average recognition accuracy of five algorithms on the AR face database and the corresponding standard deviations and dimensions %

图4为在ORL、Yale和AR标准人脸图像库上5种算法的平均识别率随特征向量维数的变化关系。图4(a)显示在ORL标准人脸图像库中实验时， 随机选择每个人的前l=4幅人脸图像作为训练样

本集,剩余的人脸图像作为测试样本集。图4(b)显示在Yale人脸图像库中试验时，随机选择每个人前l=6幅人脸图像作为训练样本集，剩余人脸图像作为测试样本集。图4(c)显示在AR人脸图像库中实验时,随机选择每个人前l=5人脸幅图像作为训练样本集,剩余的人脸图像作为测试样本集。其中，在ORL和Yale标准人脸图像库进行50次重复实验取其平均值，AR标准人脸图像库进行10次重复实验取其平均值。

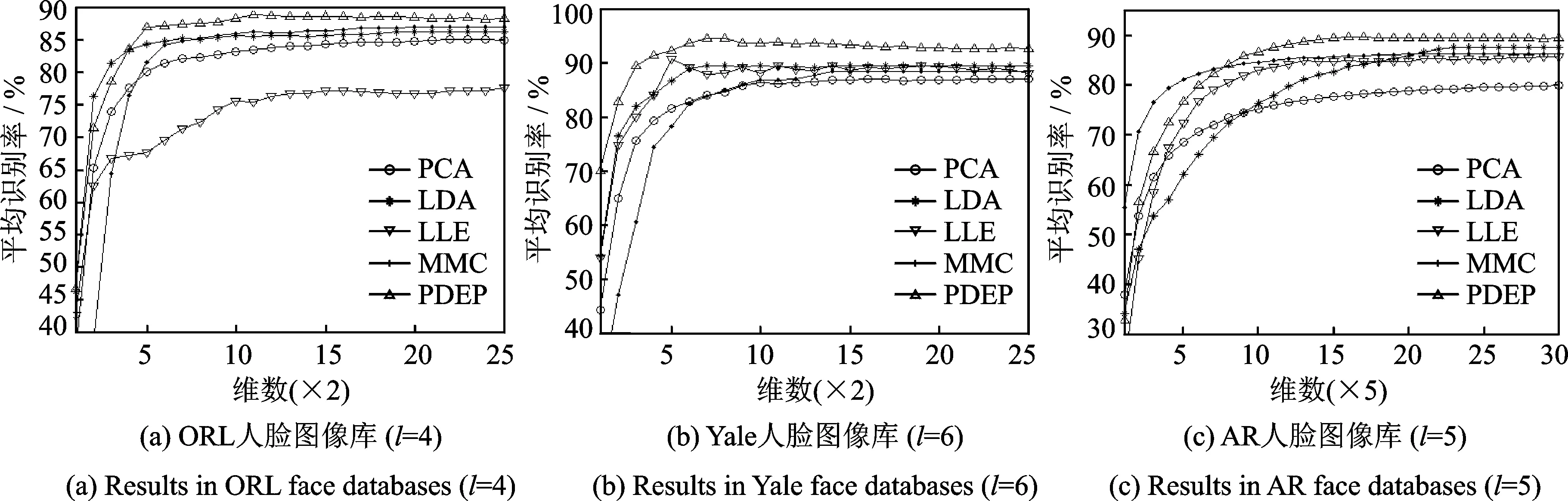
图4 FDEP算法平均识别率随特征向量维数的变化情况Fig.4 Average recognition rates of FDEP versus the corresponding varied dimensions

4.3 实验分析

从4.2节实验结果可以得到以下的结论:

(1) 从表1～3可以得到,随着训练样本的增加,5种方法的最大平均识别率也增加。在3个人脸数据库上的实验看出本文FDEP算法的结果优于其他算法。

(2) 从图4可以得到，FDEP算法在特征向量维数增大的情况下，平均识别率也一直增大；且在特征向量维数比较高时，FDEP算法的平均识别率优于PCA、LDA、LLE和MMC等算法的平均识别率。

(3) 由于FDEP算法既考虑局部近邻结构信息分布，又考虑全局结构信息的分布，使得该算法平均识别率远远优于LLE算法平均识别率。 因此，FDEP算法可以通过保持局部嵌入和全局方差得到最优映射矩阵。

5 结束语

在机器学习和模式识别中，特征提取技术被广泛地应用在人脸识别和分类上。本文主要针对流形学习LLE算法未考虑数据样本全局信息的问题，提出一种新的特征提取的方法——模糊差分嵌入投影(FDEP)算法，并将其应用在人脸库上。所提出的FDEP算法可以看作是PCA算法和LLE算法的结合，同时融合了模糊全局保持嵌入与模糊局部方法的优点，保持了局部信息和全局信息的最优。因此，相对PCA算法和LLE算法，FDEP算法可以获得更好的分类性能。在ORL，Yale和AR三个标准人脸库上的实验结果验证了FDEP算法的有效性。下一步工作将研究FDEP算法在监督和半监督学习时的性能。

[1] Swets D L,Weng J. Using discriminant eigenfeatures for image retrieval [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1996,18(8): 831-836.

[2] Kirby M,Sirovich L. Application of the KL procedure for the characterization of human faces [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,1990,12(1): 103-108.

[3] Chang K Y,Ghosh J. A unified model for probabilistic principal surfaces[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2001,23(1): 22-41.

[4] Hinton G,Dayan P,Revow M. Modeling the manifolds of images of handwritten digits[J]. IEEE Transactions on Neural Network,1997,8(1): 65-74.

[5] Gomes J,Mojsilovic A. A variational approach to recovering a manifold from sample points[C]// 7th European Conference on Computer Vision. Copenhagen:[s.n.],2002: 3-17.

[6] Saul L K,Roweis S T. Think globally,fit locally: Unsupervised learning of low dimensional manifolds [J]. Journal of Machine Learning Research,2003,4(1): 119-155.

[7] Tenenbaum J B,de Silva V,Langford J C. A global geometric frameword for nonlinear dimensionality reduction[J]. Science,2000(290): 2319-2323.

[8] Roweis S T,Saul L K. Nonlinear dimensional reduction by locally linear embedding [J]. Science,2000(290): 2323-2326.

[9] Belkin M,Niyogi P. Laplacian Eigenmaps for dimensionality reduction and data representation [J]. Neural Computation, 2003,15(6): 1373-1396.

[10] He X,Yan S,Hu Y,et al. Face recognition using Laplacianfaces [J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2005,27(3): 328-340.

[11] Yan S,Xu D,Zhang B,et al. Graph embedding and extensions: A general framework for dimensionality reduction[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence,2007,29(1): 40-51.

[12] Chen H T,Chang H W,Liu T L. Local disciminant embedding and its variants[C]// IEEE Computer Society Conference on Computer Vision and Pattern Recognition. [S.l.]:IEEE Computer Society, 2005: 846-853.

[13] 李忠国，侯杰，王凯,等. 模糊支持向量机在路面识别中的应用[J].数据采集与处理,2014，29(1):146-151.

Li Zhongguo，Hou Jie，Wang Kai，et al. Application of fuzzy support vector machine on road type recognition [J]. Journal of Data Acquisition & Processing,2014，29(1):146-151.

[14] Kwak K C,Pedrycz W. Face recognition using a fuzzy fisher classifier [J]. Pattern Recognition,2005,38(10): 1717-1732.

[15] Bezdek J C,Keller J,Krishnapuram R. Fuzzy models and algorithms for pattern recognition and image processing[M]. Dordrecht: Kluwer Academic Publishers,1999.

[16] Wan M,Zheng W. Fuzzy two-dimensional local graph embedding discriminant analysis (F2DLGEDA) with its application to face and palm biometrics [J]. Neural Computing and Applications,2013,23(1): 201-207.