基于低压电力信道的信道容量计算与分析*
张秀秀,冯晋军
(长治学院 电子信息与物理系,山西 长治 046011)
0 引 言
低压电力线通信系统利用广泛分布的电力线进行数据传输和信息交换。电力线通信具有组网方便、分布区域广等特点,因此利用电力线进行通信可以节约大量成本。近年来,电力线通信已逐步成为通信领域研究的热点。然而,电力线并不是专门为传输信号设计的,利用电力线通信存在多径效应、信号衰减和脉冲噪声干扰等问题,势必会导致低压电力线通信系统容量较低、可靠性差等问题。为解决这些问题,须围绕提高低压电力线通信系统信道容量为目的开展研究和分析。下面将简单介绍高斯白噪声信道容量的分析。
1 高斯白噪声信道容量分析
通信原理中,对于一个噪声而言,它的幅度服从高斯分布,功率谱密度是均匀分布,则这样的噪声被称作高斯白噪声。信号从带有高斯白噪声的信道中通过,输出的信号具有连续性,且信号在分布均匀时具有最大的信道容量。
信息论与编码论中,H(X)代表信源X的熵,表示信源X中每个符号的平均信息量;H(X/Y)指因信道干扰而丢失的损失熵,表示在输出端接收到全部符号Y后,发送端尚存在的平均不确定度。互信息I(X;Y)为H(X)-H(X/Y)。可见,当H(X)最大化时,互信息最大化的问题将得到解决。如果通信信道中的噪声是高斯白噪声,信号功率给定,那么传输信号的最大信道传输容量可以利用信息论中著名的香农公式[1]计算:
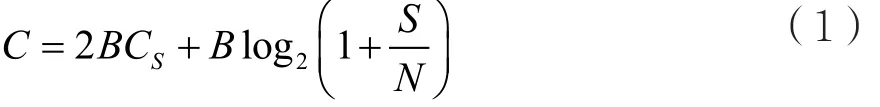
式中,C表示最大信息传送速率,B表示信道带宽(单位Hz),S是信号功率(单位W),N是噪声功率(单位W)。
2 低压电力线信道容量分析
电力线上分支多,存在各种干扰。某个时间点,在电力线上接收的信息会受这个时间点多条支路的干扰。干扰情况与分支数量有关,还与电力线上的接收位置有关。定义Np为路径数目,则Np由信道最大路径时延τmax和平均时延τm决定,有
接收到的信号为[2]:
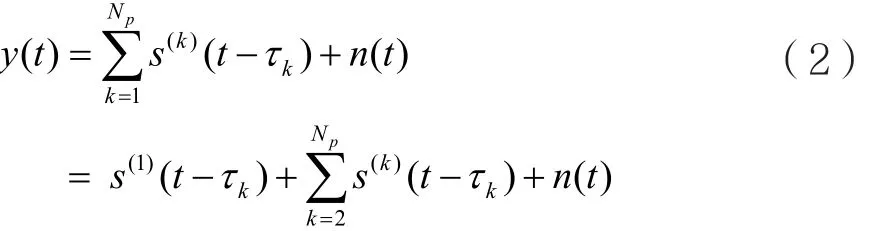
式中,s(1)(t-τk)为电力线上接收到的信号;为电力线上各支路接收到的信号,会影响s(1)(t-τk)的接收;n(t)为高斯白噪声。采用相关接收,针对α(1)0即发出的第一个信息位,接收端的输出为[2]:
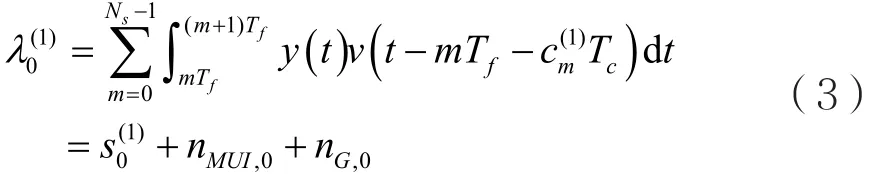
某时刻,在电力线上接收到其他支路的干扰信号为[2]:

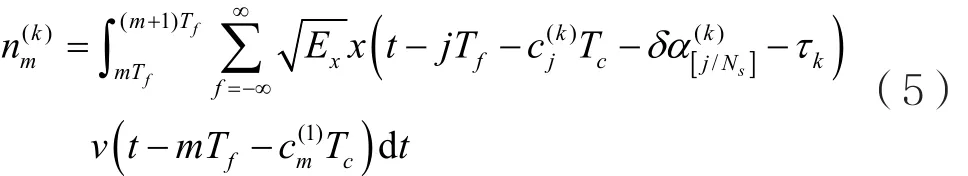
其中,τk表示第k个分支的传输时延,且设τk=NhTc,Nh∈ {0,1,2,…,Nh-1}。在某一时刻,接收端接收信息时也收到了第k个分支线路发出的干扰信息。那么,当前接收端时隙上肯定存在干扰脉冲,当前帧中的接收时隙内受到其他分支的干扰信息的概率为1/Nh。这种情况下,考虑发送x(t)与x(t-τ)等概,即当前接收时隙受到一个分支线路影响的概率为1/Nh,其中1/2的概率干扰信息为0,1/2的概率干扰信息为1。因此,若发送α(1)0=0,则有:
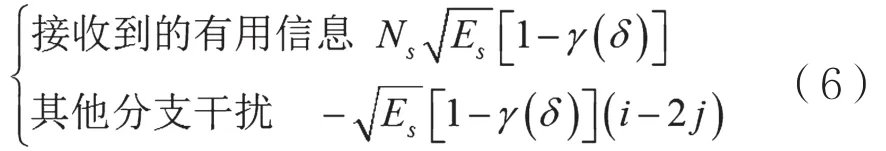
所以,概率密度函数为:

利用参考文献[3]中的电力网络,Tc=0.4 ns,δ=0.1 ns,相关系数 γ(δ)=-0.231 7;Np是路径数,Ns表示每比特信息的脉冲数,文中设定Np=7,Ns=4。如果这时信道最大路径时延τmax为2 ns或平均时延τm取0.35 ns,则电力线信道信息容量的仿真结果依次如图1、图2所示。

图1 路径τmax变化时的信道容量
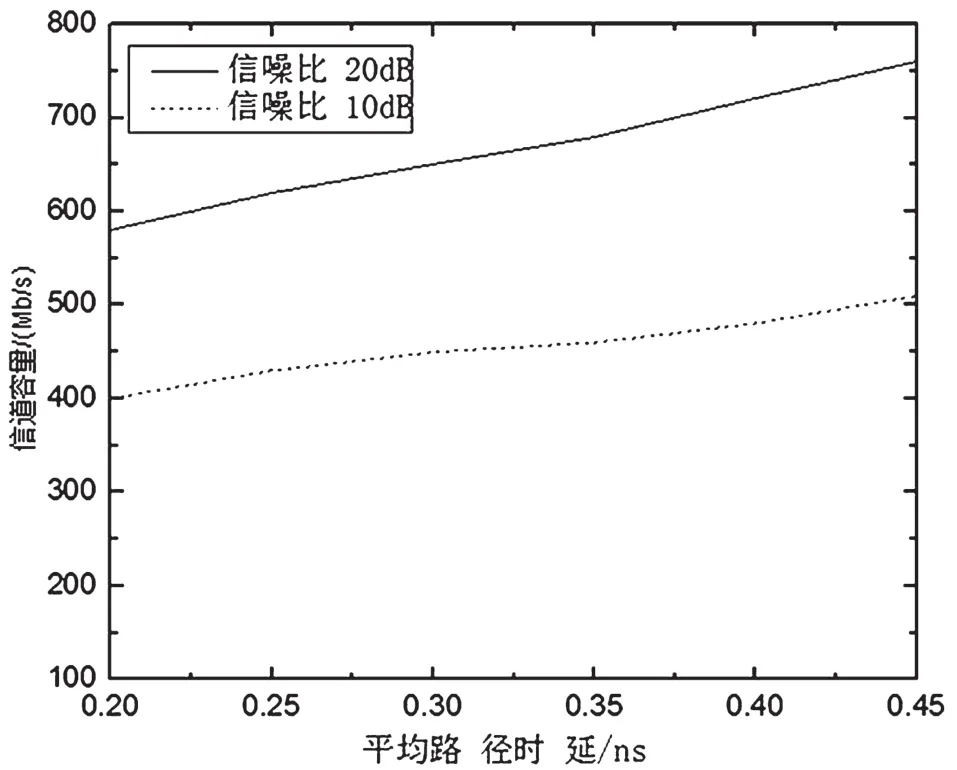
图2 路径τm变化时的信道容量
可见,在电力线抄表系统接收端,信噪比增加时,信道容量也会随之增加;τmax和τm变化时,会影响Np增多;电力线支路引起的符号间干扰增加时,电力线的信道容量减小。
3 低压抄表系统的误码率分析
通过大量的测量数据发现,可以将低压电力线上存在的噪声看成熟悉的高斯白噪声。具体地,在分析电力线上抄表系统受噪声的干扰时,可将其考虑为高斯白噪声。
高斯白噪声n(t)有[4]:

方差:
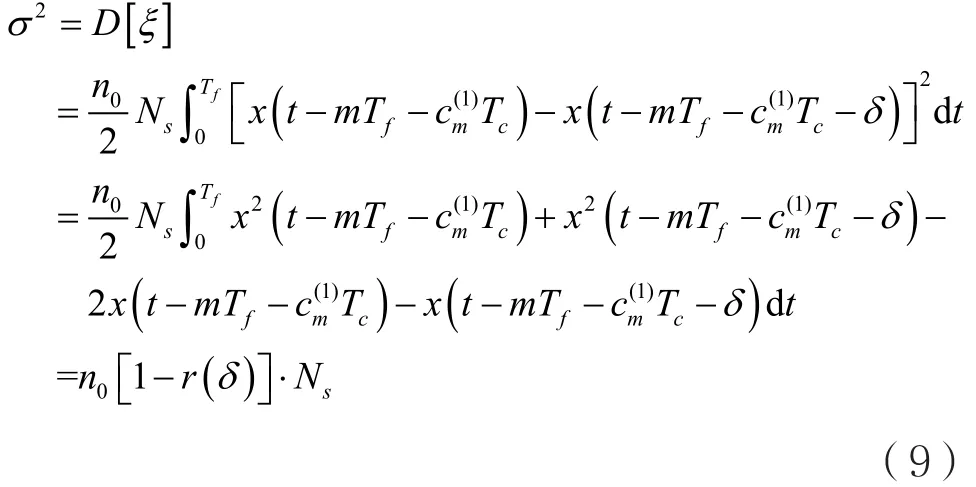
接收端输出的信号η为有用信息和干扰信息。若发送端发送信息为0时,η小于门限值0,则产生误码。如果用P(x1)表示发送x1的概率,Px1(x2)表示发送x1错判为x2的概率;P(x2)表示发送x2的概率,Px2(x1)表示发送x2错判为x1的概率,那么误码率为:
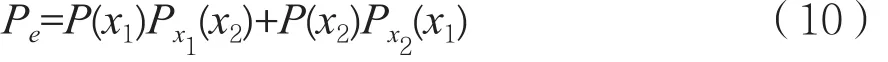
图3为高斯白噪声对抄表设备误码率的影响仿真图。仿真中,将低压电力线上的背景噪声看成高斯白噪声,通过一定范围的信噪比,得出噪声对抄表设备误码率的影响。可以清楚看到,只有信噪比达到20 dB以上时,抄表设备的误码率才能低于10-4。
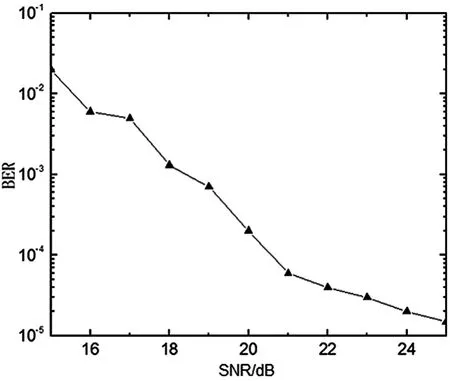
图3 高斯白噪声对抄表设备误码率的影响
4 结 语
分析高斯白噪声信道容量的计算方法,随后在此基础上分析低压电力线上信道容量的计算过程。通过仿真得出,信号信噪比增加时,信道容量增加;路径数增加,信道容量减小。最后,简要分析背景噪声对低压电力线自动抄表设备误码率的影响。
[1] John G P.现代通信系统[M].北京:电子工业出版社,2015:17-35.John G P.Modern Communication Systems[M].Beijing:Electronic Industry Press,2015:17-35.
[2] Klaus D.电力线通信[M].北京:中国电力出版社,2013:34-37.Klaus D.Power Line Communication[M].Beijing:China Electric Power Press,2013:34-37.
[3] Zimmermann M,Dostert K.A Multi-Path Signal Propagation Model for the Power Line Channel in the High Frequency Range[C].Proceedings of 3rd International Symposium on Power Line Communications and its Applications,2012,25(12):566-676.
[4] 胡广书.数字信号处理[M].北京:清华大学出版社,2012:35-37.HU Guang-shu.Digital Signal Processing[M].Beijing:Tsinghua University Press,2012:35-37.

