极化码改进串行抵消比特翻转译码算法
王 杰,郭 锐
(杭州电子科技大学,浙江 杭州 310018)
0 引 言
2008年,E.Arikan教授提出极化码(Polar Codes),是迄今为止唯一一类可以从理论上证明可达香农容限的信道编码方式。由于固定的编码结构和较低的编译码复杂度,它受到了编码界的广泛关注。E.Arikan从理论上证明,在二进制离散无记忆信道(B-DMC)下,当码长N趋于无穷大时,采用串行抵消(SC)译码算法的极化码可以达到香农容限[1-2]。然而,这却并不适用于中短码长极化码。由于信道极化不完全,极化码的SC译码算法性能不足。因此,需要寻找更优的译码方案来弥补这一不足[3-4]。为了改善SC算法的路径局部最优搜索方式,文献[5-6]提出SC译码的改进算法:串行抵消列表SCL译码算法。它的原理是在SC译码的基础上,通过保留多条候选译码判决路径,从候选路径中选取可靠度最高的路径作为译码结果,提升译码性能,其中译码复杂度为O(LNlogN)(L为列表宽度)。为了进一步提升极化码性能,文献[7]提出循环冗余校验(Cyclic Redundancy Check,CRC)辅助SCL算法,即在SCL算法基础上加入CRC校验用于译码路径判决,令中短码长的极化码性能优于LDPC码和Turbo码。针对SC译码过程的错误传播,文献[8]提出串行抵消翻转(SCFlip)算法,使用比特翻转思想对SC译码进行检错并纠错,提升SC译码性能,且在信噪比较高时,算法复杂度相对于SC译码并没有较大提高。本文在SCFlip算法的基础上,提出了基于极化特性分段策略,根据极化子信道的可靠度进行分段比特翻转,实现了多比特翻转,进一步提升了SC译码算法的性能。
1 极化码理论
1.1 极化码编码
极化码的编码过程实质是信道极化(Channel Polarization)过程[1],即通过信道组合(Channel Combining)和信道分离(Channel Splitting)将相互独立的N(N=2n)个B-DMC信道W∶X→Y转化为相互依赖的N个极化子信道∶X→Y×Xi-1。其中,X∈{0.1}表示信道输入集,Y表示信道输出集。编码时,根据各极化子信道的可靠度排列,从中选出可靠度高的K个信道传输信息比特序列,剩下N-K个可靠度低的信道传输冻结比特(一般为0),那么构造的极化码码率为R=K/N。若信息比特用集{1,2,…,N}表示,冻结比特用集合Ac≜{b1,b2,…,bk}⊆{1,2,…,N}表示,其中Ac为A的补集,那么输入序列可表示为=(uA,uAc),极化码的编码为[8]:
其 中 GN为 生 成 矩 阵,GN=BNF⊗n,(n=logN);表示基矩阵F的n次Kronecher积;BN为比特反转重排矩阵,≜{x1,x2,…,xN}表示编码序列。经过调制和信道传输后,得到接收序列≜ {y1,y2,…,yN}。
1.2 串行抵消(SC)译码算法

其中:
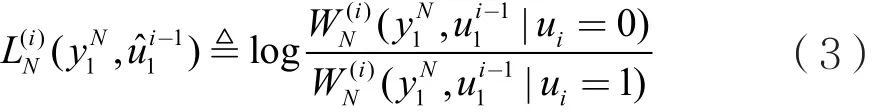
判决函数h根据对应的对数似然比做出译码判决,即:

可以直接使用迭代公式计算译码过程中的似然比:
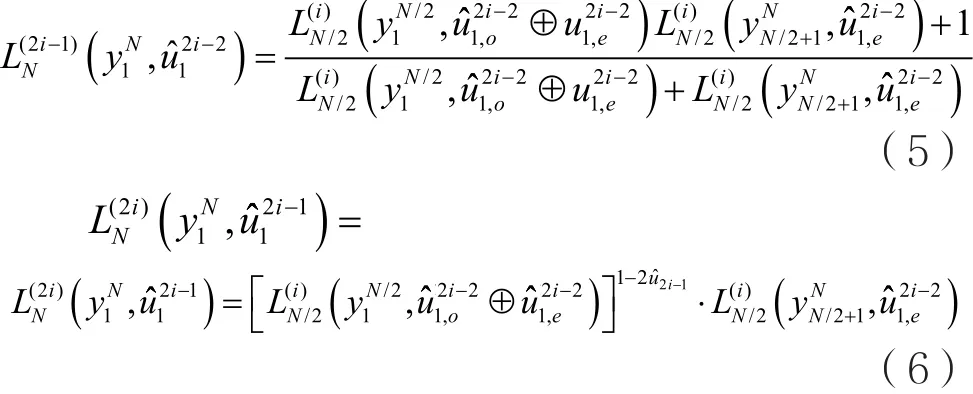
其中,似然比的初始化条件为:

2 改进串行抵消比特翻转译码算法
2.1 错误传播的影响
由式(6)可知,计算第2i个比特的对数似然比时,需要用到第2i-1个比特的译码估计值21ˆiu-。若21ˆiu-译码判决出错,则当前比特的估计值将受前一比特估计值的影响,这就是SC译码的错误传播特性。在SC译码过程中,导致译码判决出错的原因主要是信道噪声和错误传播。文献[9]提出了能自动纠错的SC Oracle译码器来探究错误传播对SC译码性能的影响。因为这种译码器能够消除错误传播的影响,所以需要纠正的错误比特则均是由信道噪声产生的。为了直观地统计数据,采用全零码字传输,在500 000次仿真实验下,统计了各错误帧中地误比特数,结果如表1、表2所示。

表1 不同信噪比下错误位数比例(N=1 024)

表2 不同码长下错误位数比例(SNR=2 dB)
根据表1、表2可知,在所有错误帧中,单比特错误帧占据的比例随信噪比和码长的增加越来越大。以码长N=512为例,信噪比Eb/N0=2时,帧内错误比特数均不超过4位,其中单比特错误帧的比例为74.6%,2~4比特错误帧占据的比例为25.4%。SCFlip算法仅能翻转单个比特,而没有多比特纠错能力,虽然能够在一定程度上提升译码性能,但对于剩余的25.4%的多比特错误块,SCFlip算法无法得到正确的译码码字,这就是SCFlip算法的局限性。因此,在改善SC算法的错误传播特性上,SCFlip算法存在较大的改进空间。
2.2 分段校验极化码构造
针对SCFlip算法的局限性,本文提出采用分段策略的改进SCFlip算法。具体地,将信息序列按照一定的方法分段,每段均加入校验比特用以检错,实现段内单比特翻转和整体多比特翻转,且翻转比特数即为分段数,以获得针对多比特错误块的修正能力,进一步抑制错误传播的影响。本文提出的信息序列的分段方法有均匀分段和基于极化特性分段两种方式。
2.2.1 均匀分段构造
所谓均匀分段,就是每段的比特数是相等的,即M=K/P,其中K是极化码的非冻结比特数,P表示均匀分段数。校验比特一般放在每段的最后,本文选择3位奇偶校验,那么每段中的信息序列数为M-3,每段的比特分布则可以表示为:
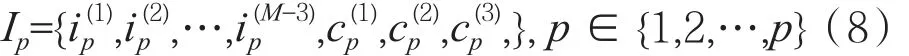

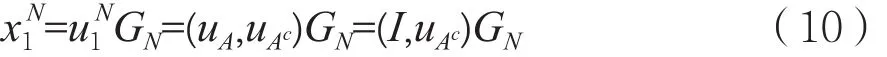
均匀分段构造虽然可以获得一定的性能提升,但错误比特不一定均匀分布在信息序列中,而此分段依据并没有考虑错误比特数密集的区域。由于本文所提算法每段内仅能翻转单个比特,故所取分段方式要在最大程度上保证错误比特均匀分散在每段内,且保证段内错误比特数尽可能少。
2.2.2 基于极化特性分段构造
基于极化特性分段构造,利用极化子信道的不同可靠性,以极化子信道的错误概率分布作为分段依据[10]。在本文采用的AWGN信道中,用高斯近似方法计算各极化子信道的错误概率[11],并绘制出码长N=256、码率R=0.5、信噪比Eb/NO=1 dB的传输非冻结比特信道的错误概率分布图,如图1所示。从图1可以观察到,非冻结比特信道的错误概率中存在错误突发段。错误突发段是由于信道极化过程中部分错误概率较高的非冻结比特信道非均匀散落于所有信息信道中,导致某些信道的错误概率急剧增加。图1中虚线右边的错误概率突然急剧增加,如此可以将该信息序列按错误突发情况分为4段。一般情况下,错误突发段的选择标准如下:与突发错误点邻接的两信道的错误概率差距远大于其他相邻信道之间的错误概率差。
基于极化特性分段构造标准,以错误突发点为分割线(如图1中的虚线位置),将信息序列非均匀地分为P段,每段最后3位作为CRC校验位。假设第p段包含L个信息信道索引,那么每段的比特分布可用式(11)表示:

以错误突发段进行分段的优势为:
第一,避免将错误比特密集段分于同一段内,基本保证错误比特能均匀分布于每段。又由于本算法段内每次仅能翻转一位比特,那么段内误比特数目越少,翻转成功率越高,译码错误率也就越低。
第二,分段处理增加比特翻转机会,且分段数是可翻转比特数,总体看来可以实现多比特翻转。
2.3 改进串行抵消比特翻转译码算法
本文所提的改进SCFlip算法,以分段构造的方式增加校验次数和比特翻转次数,降低了极化码译码的突发错误概率和错误传播的影响。新算法编码阶段加入的奇偶校验位,能够在译码阶段对译码估计序列进行检错,根据奇偶校验结果,判定错误比特可能的位置,判定结果见表3。
根据上述内容,新算法的具体流程如下(针对基于极化特性分段构造):
步骤1:通过高斯近似法计算极化子信道错误概率,并根据错误概率划分信息序列,从而确定分段数目P和待翻转比特位数T,同时记录每段截止位的信道索引集合,记为:Ind={ind1,ind2,…,indp}。按照2.2.2中方法添加奇偶校验位进行极化码编码,得到编码码字。
步骤3:当SC译码进行到每一段的截止位时,即完成信道索引i=indp,p∈{1,2,…, p}(假设此时译码进行到第p段)所传输的比特的译码判决,然后进行奇偶校验,根据校验结果确定判定结果。如果判定结果为未出错,执行步骤5;否则,对对应索引位置的按升序排列,取其中前T个最小的,以对应的信道索引i构造待翻转比特集合Flip={F1,F2,…,FT},执行步骤4。

表3 错误比特位置判定结果
步骤4:比特翻转阶段,从集合Flip中选取F1位对应的比特进行翻转,并对F1+1位到indp位的比特重新执行SC译码和奇偶校验。若译码结果仍未通过奇偶校验,先还原F1位对应的比特值,选取Flip中F2位对应的比特执行翻转操作。后续过程同前。若遍历集合Flip仍未得到有效码字,则说明翻转失败,以初始SC译码作为本段译码结果,然后执行步骤5;若存在一次译码结果通过奇偶校验,则停止翻转,执行步骤5。
步骤5:对信道索引i∈(indp,indp+1)之间的比特继续进行SC译码,在对indp+1位比特判决后进行奇偶校验,后续比特翻转操作同步骤3。
步骤6:按上述方式分段译码、多次校验、执行比特翻转,直到译码结束,得到译码估计码字。
3 系统仿真与性能分析
对本文提出的改进SC比特翻转算法(分别采用均匀构造和基于极化特性构造)进行仿真分析,主要分析误比特率、误帧率,并与文献[1]中提出的SC算法、文献[5-6]中提出的SCL算法(L=2)、
文献[8]中提出的SCFlip算法进行比较。本仿真在AWGN信道下进行,设码字的有效码率为0.5,SCFlip算法,待翻转比特数T1=16,新算法的每段待翻转比特数T2=8。图2、图3分别为码长N=256时的误比特率和误帧率曲线,新算法分段数P=4;图4、图5分别为码长N=256时的误比特率和误帧率曲线,新算法分段数P=6;图6、图7分别为码长N=1 024时的误比特率和误帧率曲线。新算法分段数P=8。

图2 N=256各译码算法误比特率
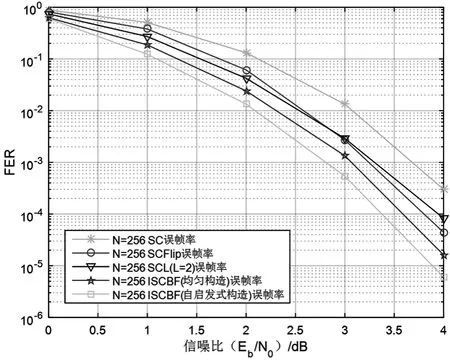
图3 N=256各译码算法误帧率

图4 N=512各译码算法误比特率
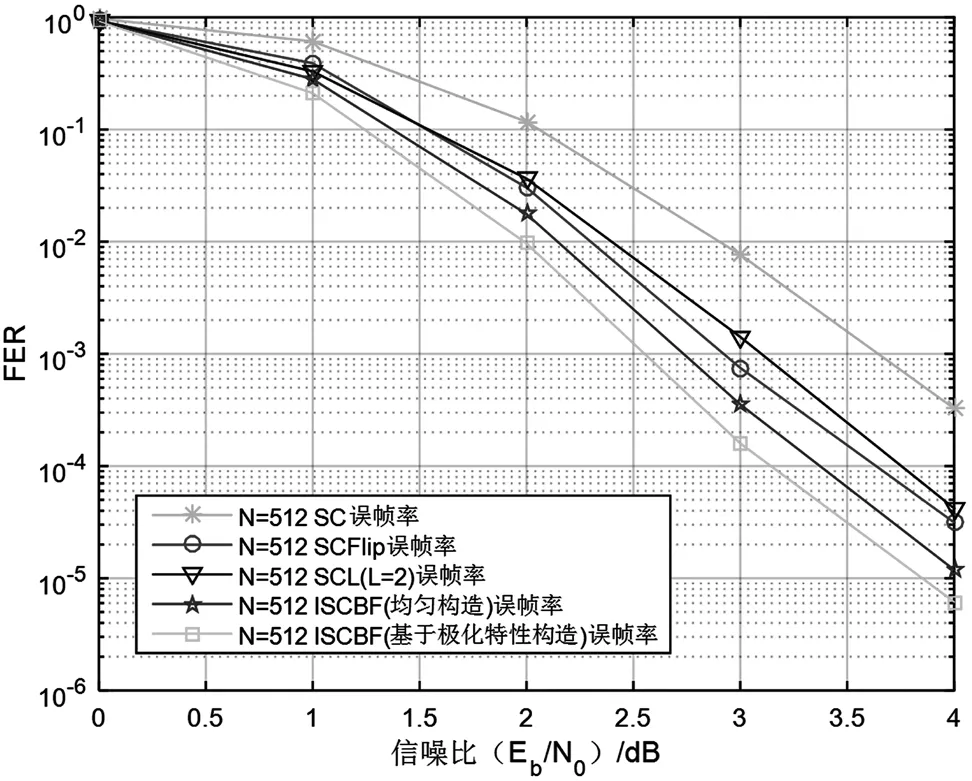
图5 N=512各译码算法误帧率
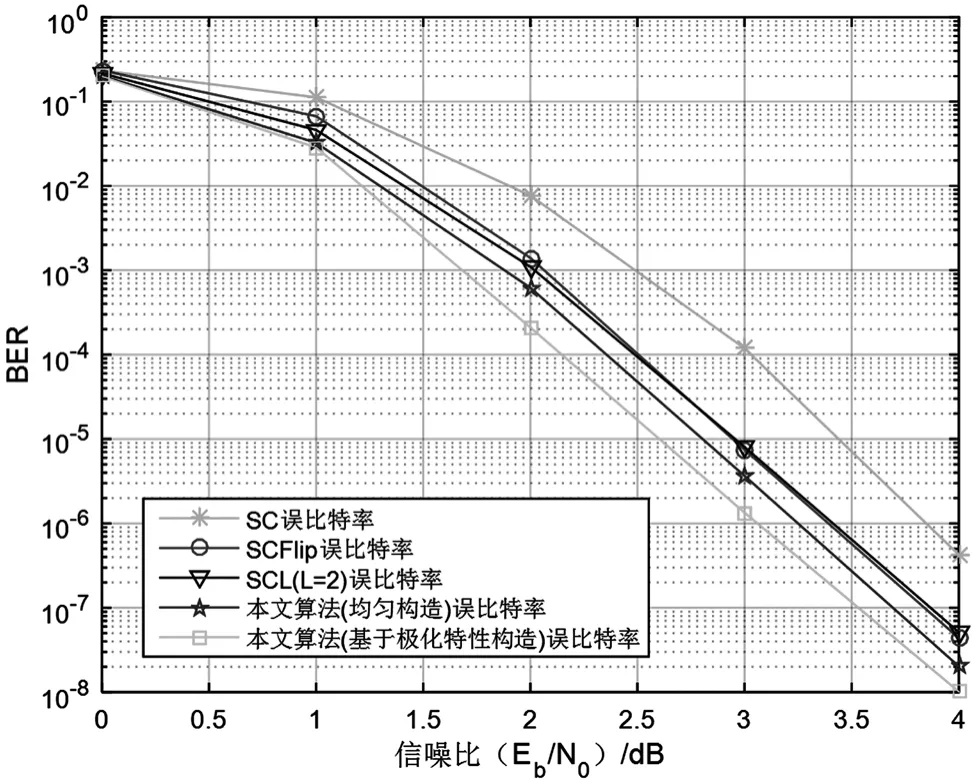
图6 N=1 024各译码算法误比特率

图7 N=1 024各译码算法误帧率
由仿真结果可知,本文提出的改进SC比特翻转译码算法性能明显优于SC译码、SCL(L=2)算法和SCFlip算法。因为新算法能够实现多次翻转,在SCFlip算法的基础上能更大程度抑制SC译码中出现的错误传播特性和突发错误。另外,在信噪比不大于1 dB时,新算法性能提升有限。这是由于信道条件差会导致错误比特较多,导致新算法无法取得较好的翻转效果。仿真结果也表明,基于极化特性分段构造的改进SC比特翻转算法性能略优于基于均匀构造的改进SC比特翻转算法性能。这是因为在信息序列的分段上,基于极化特性分段方式能够从错误比特出现位置角度考虑分段位置,而不是从信息序列整体角度考虑,并结合极化码的信道极化特性,将译码出错比特尽可能均匀分布到各段中,并保证每段内的错误比特数尽可能少,以提高比特翻转的纠错能力。
表4给出码长N=1 024、在误帧率为10-4时,本文提出的新算法相比于其他已有算法获得的增益。由表4可知,相比SCFlip算法,本文提出的算法(基于极化特性构造)获得了约0.28 dB的增益;相比SCL(L=2)算法,获得了约0.33 dB的增益;相比SC算法,获得了约0.74 dB的增益。此外,基于基于极化特性构造的新算法性能略好于基于均匀构造的新算法的性能,获得了约0.13 dB的增益。

表4 FER=10-4时,新算法获得的性能增益统计
4 结 语
针对极化码的错误传播特性,本文提出了改进SC比特翻转译码算法。该算法采取对信息位分段校验的方式,增加比特翻转次数,及时纠正错误比特,实现了多比特翻转,抑制错误传播的效果更好。仿真结果表明,文中提出基于极化特性分段构造方式,能合理利用极化码的极化效应,使得错误比特能尽可能均匀分布于每段,降低段内存在多比特错误的概率,进一步提升译码性能。结合仿真结果分析,与已有的SC算法、SCL(L=2)算法、SCFlip算法相比,本文提出的算法可分别获得约0.74 dB、0.33 dB、0.28 dB的增益。
[1] Arikan E.Channel Polarization:A Method for Constructing Capacity-Achieving Codes for Symmetric Binary-Input Memoryless Channels[J].IEEE Transactions on Information Theory,2008,55(07):3051-3073.
[2] Tal I,Vardy A.How to Construct Polar Codes[J].IEEE Transactions on Information Theory,2013,59(10):6562-6582.
[3] Trifonov P,Miloslavskaya V.Polar Subcodes[J].IEEE Journal on Selected Areas in Communicatio ns,2015,34(02):254-266.
[4] Trifonov P.Efficient Design and Decoding of Polar Codes[J].IEEE Transactions on Communicatio ns,2012,60(11):3221-3227.
[5] Chen K,Niu K,Lin J R.List Successive Cancellation Decoding of Polar Codes[J].Electronics Letters,2012,48(09):500-501.
[6] T a l I,V a r d y A.L i s t D e c o d i n g o f P o l a r Codes[J].IEEE Transactions on Information Theory,2012,61(05):2213-2226.
[7] Niu K,Chen K.CRC-Aided Decoding of Polar Codes[J].IEEE Communications Letters,2012,16(10):1668-1671.
[8] 郭锐,王美洁,王杰.基于缩短极化码的MLC NAND Flash差错控制技术研究[J].电子与信息学报,2017,39(07):1658-1665.GUO Rui,WANG Mei-jie,WANG Jie.Research on the MLC Nand Flash Error Control Technology Based on Polar Codes[J].Journal of Electronics & Information Tech nology,2017,39(07):1658-1665.
[9] Afisiadis O,Balatsoukas-Stimming A,Burg A.A Low-complexity Improved Successive Cancellation Decoder for Polar Codes[C].Signals,Systems and Computers,2014:2116-2120.
[10] Wang T,Qu D,Jiang T.Parity-Check-Concatenated Polar Codes[J].IEEE Communications Letters,2016(99):1.
[11] 崔茵,袁辽,倪卫明.高斯信道下极化码的子信道错误概率计算[J].微型电脑应用,2017,33(02):58-61.CUI Yin,YUAN Liao,NI Wei-ming.Calculation of Sub-Channel’s Error Probability of Polar Code under AWGN Channel[J].Microcomputer Applications,2017,33(02):58-61.

