对失效卫星特征点的自适应位姿跟踪控制
,,*,,
1. 北京航空航天大学 宇航学院,北京 100191 2. 中国科学院 空间应用工程与技术中心 中国科学院太空应用重点实验室,北京 100094
对失效航天器的在轨操作对于航天技术的长远发展意义重大。为对其进行相应操作,需要服务航天器在失效卫星附近停靠以便机械臂等设备工作。面向非合作航天器的自主停靠技术是实施对失效目标近距离停靠和对失效卫星跟踪瞄准的基础。为保证安全,避免顾此失彼,同时完成对两卫星间相对位置和相对姿态的跟踪,有必要建立追踪航天器与目标航天器的相对位姿动力学模型,并设计控制器以实现跟踪相对位姿的期望状态[1-2]。
为解决这一问题,文献[3]给出了主动航天器本体坐标系下的相对姿轨耦合动力学方程,并设计了自适应控制律。文献[4]利用状态相关黎卡提方程设计了姿轨跟踪控制器。文献[5]在姿轨耦合模型下设计了最优滑模控制器。文献[6]提出了基于对偶四元数的自适应位姿跟踪方法。文献[7]进一步从减小能量的角度优化了自适应位姿跟踪控制器。文献[8]在考虑存在模型不确定性下设计了自适应姿轨耦合控制器。文献[9]进一步拓展存在质量不确定性和扰动不确定性下的控制器设计。文献[10]采用Lyapunov最小-最大方法在视线坐标系下设计了自主接近随动跟踪控制器。文献[11]根据目标卫星的绕飞指向任务需求设计了相应控制器。文献[12]考虑了结合对接机构的相对姿态轨道耦合动力学模型。文献[13]分析了姿轨耦合项并设计了θ-D次优控制器。
以上的研究工作较好地解决了对目标星和追踪星质心之间的相对位姿进行建模与控制问题,但对目标上的特征点停靠及姿态跟踪瞄准任务的研究仍存在不足。事实上,对于非合作目标,若要对其实现精准的在轨操作(如零部件替换等),则对其上某些特殊位置的悬停及视线跟瞄是必不可少的。且在这一过程中,由于系统存在多种外界未知扰动,以及系统惯性参数不可精确测量获得,因此对系统的抗干扰能力及其鲁棒性提出了较高要求。
为弥补这一不足,文章将对失效卫星上的特征点跟踪问题转化为传统的对质心跟踪问题。并基于自适应控制理论,设计了针对包含追踪星质量、追踪星转动惯量、系统所受扰动力、扰动力矩和失效卫星转动惯量在内的5种不确定性的复合自适应反馈控制器。同时,文章对于执行机构受限情况下,设计了控制参数调节过程并对输出采取限幅措施。
1 相对运动模型
1.1 坐标系建立
为方便问题描述,采取如下坐标系:
1)地心惯性坐标系Oxiyizi(i系)。
2)定义目标星本体坐标系Oxbtybtzbt(bt系)。
3)追踪星本体坐标系Oxbcybczbc(bc系),假设xbc轴上搭载有对目标观测的星载敏感器。
4)参考坐标系Oxdydzd(d系),原点在追踪航天器质心,xd轴指向目标星特征点,其他两轴与xd轴的关系与ybc和zbc与xbc的关系一致。
1.2 问题描述
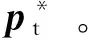

图1 相对位置关系示意Fig.1 Relative position relationship diagram
定义S(w)∈R3×3,对向量w=[w1,w2,w3]T满足:
在bc系下,追踪星的质心C满足[14]:
(1)
式中:qc=[qc1,qc2,qc3,qc4]T是表示追踪星姿态的四元数;{rc,vc,qc,ωc}分别为bc系下的质心C相对于惯性系的位置、速度、姿态和角速度,{f,df}分别为bc系下的质心C所受到的控制力和扰动力,{τ,dτ}分别为bc下质心C所受到的控制力矩和扰动力矩,{m,Jc}分别为追踪星的质量和转动惯量;Ω(qc)为姿态矩阵。
假设目标星无机动,并忽略目标星所受干扰力及干扰力矩,则目标星的旋转状态被简化为零干扰零机动情况下的自然旋转演化状态。在目标星本体坐标系bt下,目标星质心T满足如下方程[14]:
(2)
式中:qt=[qt1,qt2,qt3,qt4]T;{rt,vt,qt,ωt}分别为bt系下质心T相对于惯性系的位置、速度、姿态和角速度;Jt为目标星的转动惯量。
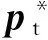
1.3 期望相对位置与姿态
对目标星上的特征点S直接进行相对动力学建模并设计对其悬停控制的方法较为复杂,此处通过目标特征点S与目标质心T之间的几何关系,将对目标特征点的S悬停问题转化为对目标质心T的悬停问题。
为使追踪星上的敏感器对准目标星上特征点S,需使前文定义的追踪星本体坐标系中的xbc轴指向该点,如图2所示。
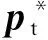
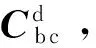

(3)
1.4 相对动力学模型
在图1中,用{vt,vpt}分别表示bt系下目标星质心T和P点相对于惯性系原点的速度,则可得:
(4)
则追踪星质心C相对于目标星质心T的相对位置、相对速度,相对于目标星的相对角速度、相对姿态{re,ve}可表示为:
(5)
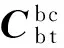
设qe=[qe1,qe2,qe3,qe4]T,{qe,ωe}为表示追踪星相对于目标星的相对姿态与相对角速度:
(6)
式中:M(qc)为计算四元数差值的特殊矩阵:
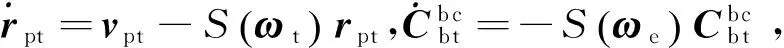
(7)
其中,
2 控制律设计
2.1 位姿联合自适应控制律

假设1:转动惯量Jc和Jt均是对称矩阵。
假设2:df和dτ是有界的。
假设3:各状态量的初始值是已知的。
假设4:变量{rc,vc,qc,ωc}可通过追踪星上安装的传感器直接得到,变量{re,ve,qe,ωe}可通过追踪星上携带的测量设备得到(ωt可由ωc和ωe做差得到)。
假设5:追踪星上搭载的姿态与轨道发动机均为理想的连续变推力发动机。给出控制律如下:
(8)
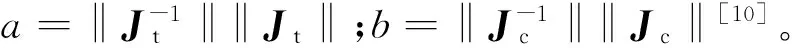
(9)
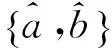
2.2 闭环系统稳定性证明
(10)
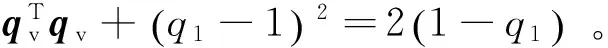
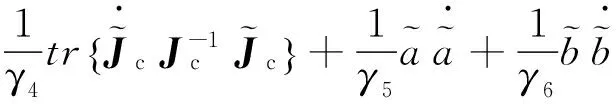
(11)
定义:
(12)
(13)
(14)
利用关系:
可得:
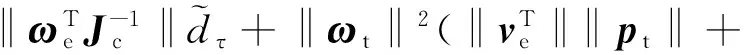
(15)
(16)
则有:
(17)
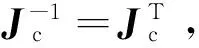
(18)
将式(18)带入式(17),可得:
(19)
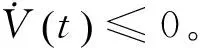
2.3 执行机构输出受限下的改进措施
式(9)中所设计的控制律在不考虑追踪星执行机构能力的情况下可以直接使用,但在初始偏差较大的情况下,可能会造成初期{f,τ}数值较大的情况,使得执行机构难以满足输出要求。为了改进这一问题,此处对{u1,u2}中的控制参数大小进行一定程度的调节:
(20)
(i=1,2,3,4)
(21)
除此之外,还可人为对{f,τ}的数值进行强制限幅,定义限幅函数sat(κ,ε),其中κ为任意实数,ε为任意非负实数:
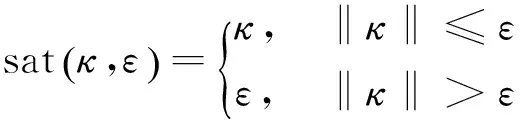
(22)
对{f,τ}做限幅处理如下:
fi=sat(fi,εf),τi=sat(τi,ετ),i=x,y,z
(23)
式中:εf和ετ为设定推力和推力矩的限定最大输出值。通过强制限幅,可使得输出满足既定要求。但限定值的大小需选取得当。否则,限定值过小容易造成系统发散,难以收敛。
3 数值仿真
3.1 对失效卫星特征点悬停指向数值仿真
假设失效卫星(目标星)在太空中不受干扰且无机动,呈自然旋转状态,初始姿态相对于惯性系为qt=[1,0,0,0]T,并假失效卫星的初始角速度为ωt=[0.1,0.1,0.1]Trad/s。在满足安全条件的情况下,追踪星对目标星上一特征点S进行悬停。仿真期望目标为:对目标星特征点进行悬停,同时使追踪星上搭载的敏感器(搭载于xbc轴上)指向特征点。
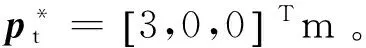
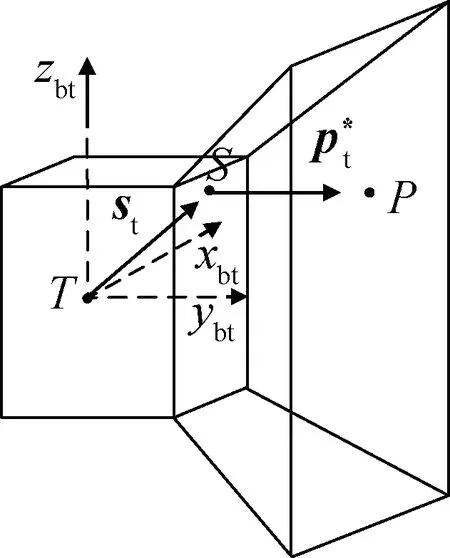
图3 目标星上特征点与期望悬停位置示意Fig.3 Diagram of characteristic points on target and desired hovering position
取追踪星与目标星的初始状态相关参数如表1所示。

表1 初始状态相关参数
假设追踪星的实际质量为m=450 kg,追踪星和失效卫星的转动惯量(单位kg·m2)分别如下:
假设,追踪星受如下干扰力和干扰力矩:
df=0.2[sin(0.01t),cos(0.01t),-sin(0.01t)]TN
dτ= 0.2[cos(0.01t),sin(0.01t),
-cos(0.01t)]TN·m
控制器相关参数如表2所示,自适应参数初始值如表3所示。
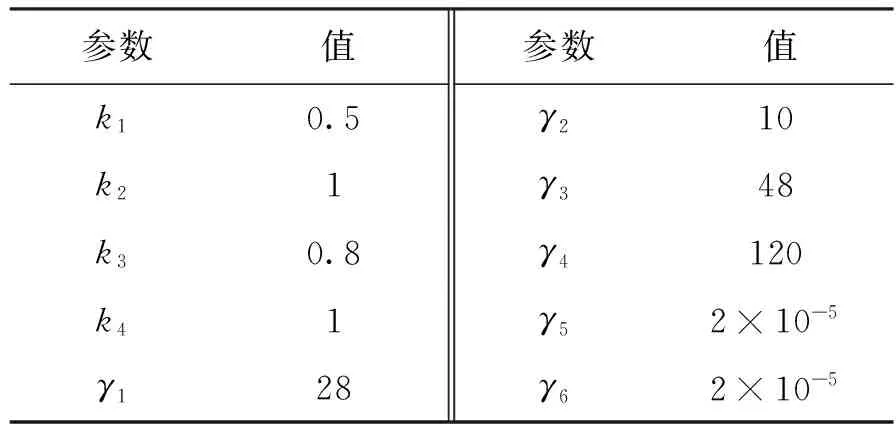
表2 控制相关参数

表3 自适应参数初始值
取仿真时间50 s,仿真步长0.1 s,采用第2.1节中的控制率,仿真结果如图4所示。
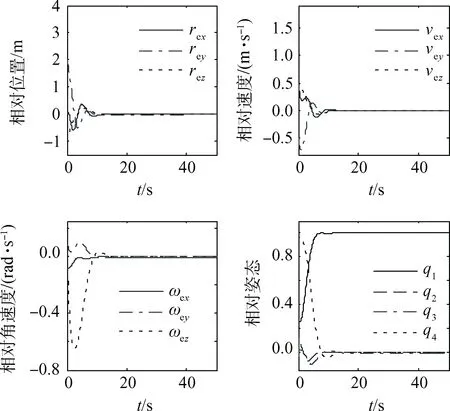
图4 各相对状态跟踪误差Fig.4 Relative state tracking error
由图4可知,当初始状态给定后,随着时间推移,相对位置、相对姿态、相对速度,以及相对角速度都渐渐趋近于0。20 s后,系统基本稳定。以上结果表明,上文给出的自适应位姿联合控制律在存在不确定有界干扰力、不确定干扰力矩和存在不确定追踪星质量、转动惯量的情况下,能够实现预期位姿跟踪效果。相对位置误差、相对姿态误差、相对速度误差,以及相对角速度误差在自适应位姿联合控制律下,均能以较高精度收敛,表明了控制律的有效性。
为了确定上文给出的自适应控制律在仿真算例中对各相对变量的末端控制误差量级,取45~50 s时观察各相对变量,如图5所示。
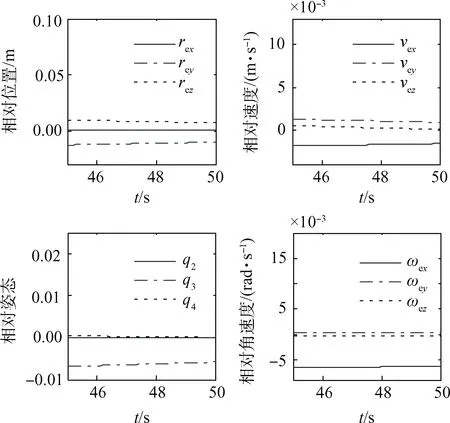
图5 稳定时各相对误差Fig.5 Relative state error in stable situation
由图5可知,在45~50 s末端稳定状态时,相对位置误差(约1 cm)和相对姿态误差(转为角度误差后约0.01°)在10-2量级,相对速度和相对角速度误差在10-3量级。除去控制参数的影响,引起位置跟踪误差的原因还与目标星的旋转有关。由于特征点跟随目标星旋转,其悬停点亦随之变化,故追踪星不得不时时追踪悬停点,这也是对特征点悬停与传统质心悬停的区别所在。对于姿态误差,受转动惯量不确定性的影响相对较大,这是由于转动惯量是三维矩阵,对系统影响比其他的不确定项更明显,对姿态跟踪造成一定难度。但考虑到追踪星的观测器件(如相机等)一般均具有一定视场,故此误差仍可被接受。
3.2 不确定性参数增大后的数值仿真
为观察追踪星的质量m、转动惯量Jc、追踪星所受干扰力df、干扰力矩dτ及目标星的转动惯量Jt的不确定性对系统的影响。使第3.1节中算例m的值和Jc、Jt的主对角线值设置为每秒递减3个单位,并将df和dτ放大50倍,其他条件同第3.1节,再次仿真,结果图6所示。
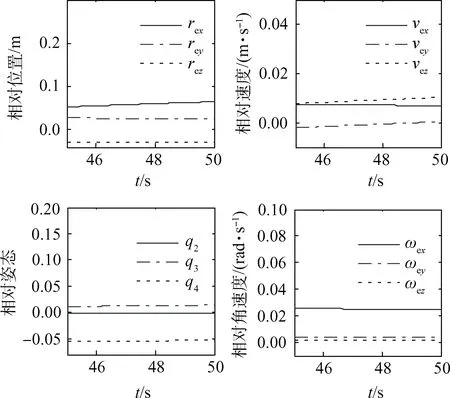
图6 增加偏差后的跟踪曲线Fig.6 Tracking curves with adding deviations
由图6可得,系统在受到追踪星的质量m、转动惯量Jc、目标星转动惯量Jt和追踪星所受干扰力df及干扰力矩dτ多种偏差共同干扰时,位置跟踪误差增至约7 cm,姿态跟踪误差增至约0.1°(由四元数转化而得),速度和角速度跟踪精度下降1个量级。可见,各相对状态在自适应控制律的作用下,仍然能够以较高精度收敛,系统具有较强的鲁棒性。
3.3 输出受限下的数值仿真
为验证输出受限状态对系统的影响,此处采用第2.3节中对控制律进行的改进。选取控制律调节参数Fk1=3.4,Fk2=3.8,Fk3=1.8,Fk4=2.2,最大输出力εf=50 N和最大输出力矩ετ=20 N·m。其他仿真条件见第3.1节,数值仿真结果如图7~9所示。
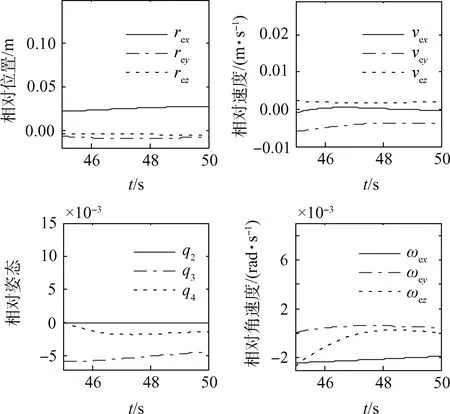
图7 调节参数后各相对误差Fig.7 Relative state error after adjusting parameters
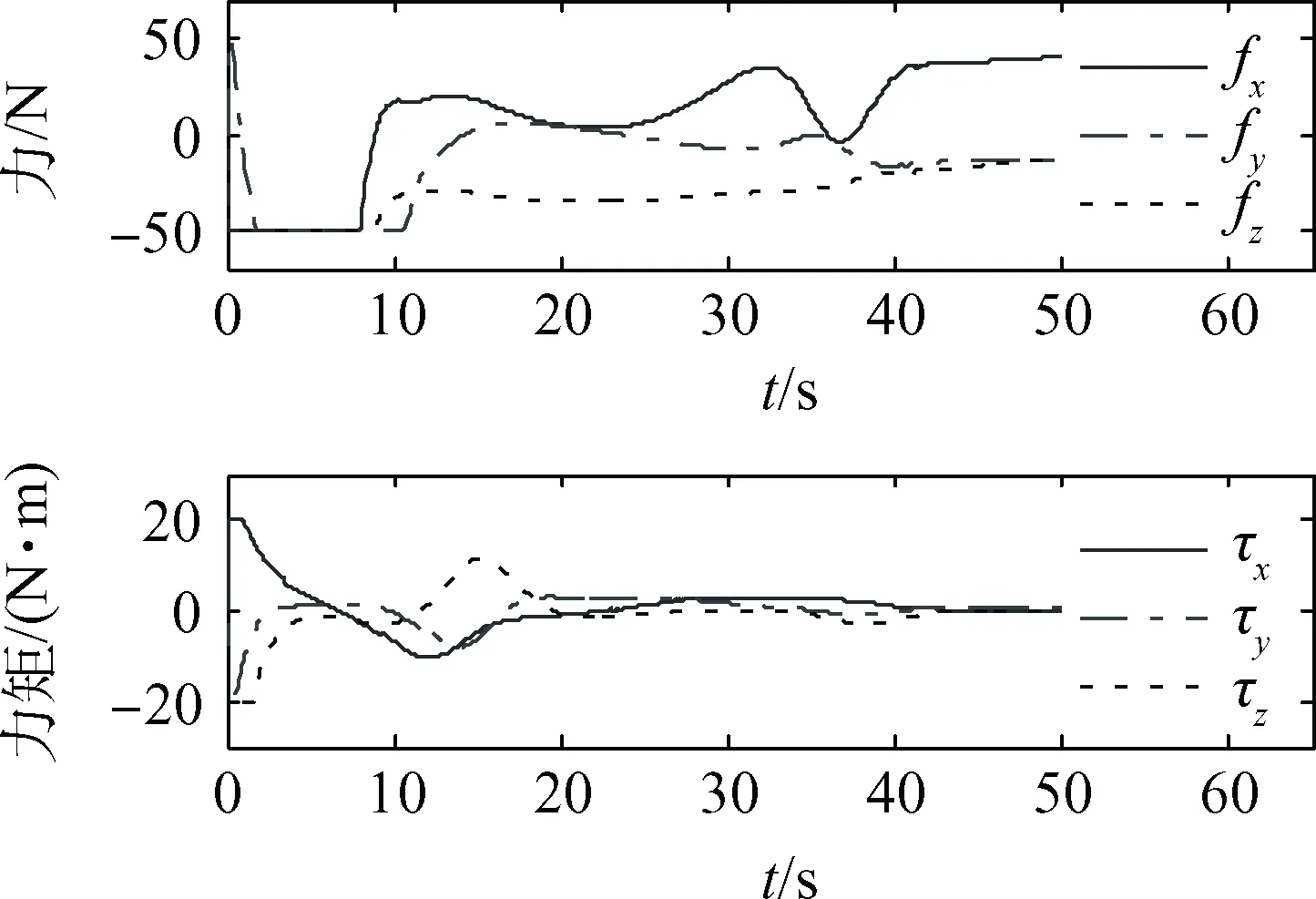
图8 调节参数后的控制力与控制力矩Fig.8 Control force and control moment after adjusting parameters
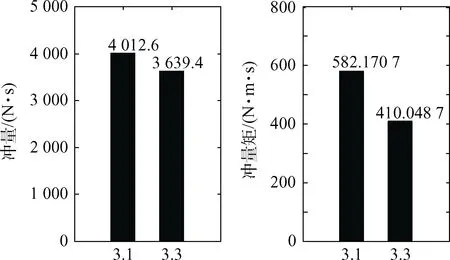
图9 调节参数后的控制力与控制力矩Fig.9 Control force and control moment after adjusting parameters
为计算悬停指向过程代价,用Ef和Eτ分别表示平动和转动所需冲和冲量矩:
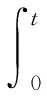

(24)
按照式(24)分别计算不考虑输入受限改进措施时(第3.1节中算例)所需冲量与冲量矩与考虑后所需的冲量与冲量矩,作如下对比(横坐标3.1和3.3分别表示第3.1节和第3.3节中的算例)。
结合图7和图4可看出,对输出受限情况施加调节措施后,相对位置、速度、姿态、角速度跟踪误差量级未改变。结合图8可知,调节后的控制力与控制力矩可按照设定最大值进行限幅,有效地限定了系统所需输出。图9对比了第3.1节中未调节的算例需求冲量和冲量矩与此处(第3.3节)调节后的算例需求冲量和冲量矩,可看出调节后的算例需求冲量和冲量矩均有下降。其中,所需冲量下降9%,所需冲量矩下降30%。可见,增加控制参数调节环节和限幅后,系统可在几乎不影响跟踪精度的情况下限定输出,同时减小所需总能量。
综上所述,针对追踪星对失效卫星上特征点的位置悬停和姿态跟踪瞄准任务,在存在目标性转动惯量、追踪星质量、转动惯量和追踪星所受扰动力和扰动力矩不确定性的情况下,相对于任务期望状态的相对位置、相对姿态、相对速度和相对角速度在位姿跟踪自适应控制律的作用下可在有限时间内收敛,且跟踪精度高。在各不确定项参数拉偏的情况下,追踪星仍然可以较高精度完成任务,系统具有较强鲁棒性。在针对输出受限情况添加控制参数调节环节并对控制力与控制力矩限幅后,系统能在不影响跟踪精度的情况下按设定值限制输出并减小跟踪所需能量。
4 结束语
论文提出了一种在满足姿态跟踪瞄准情况下针对失效卫星上特征点的悬停的控制方法,通过上述研究工作得到的结论如下:
1)给出的自适应位姿控制律使得追踪星在存在追踪星质量、转动惯量、所受扰动力、扰动力矩和目标星转动惯量不确定性的情况下完成对失效卫星上特征点的位置悬停和姿态跟踪瞄准任务。
2)在数值仿真条件下,稳定时的跟踪相对位置和相对姿态误差在10-2量级;相对速度和相对角速度误差在10-3量级。
4)在拉偏追踪星的质量和转动惯量值,放大追踪星所受扰动和扰动力倍数的情况下,相对位置与姿态跟踪误差分别增至约7 cm和0.1°,速度和角速度跟踪精度下降1个量级。
5)针对输出受限,调节控制参数同时对控制力与控制力矩限幅后,系统跟踪精度不变,所需控制力与力矩可在规定范围内,同时系统跟踪所需冲量减小9%,冲量矩减小30%。
论文所提出的自适应位姿跟踪方法对失效卫星特征点位姿跟踪任务具有一定参考价值。
References)
[1] 崔乃刚,王平,郭继峰,等. 空间在轨服务技术发展综述[J]. 宇航学报,2007,28(4):805-811.
CUI N G,WANG P,GUO J F,et al. A review of on-orbit servicing[J]. Journal of Astronautics,2007,28(4):805-811 (in Chinese).
[2] 梁斌,杜晓东,李成,等. 空间机器人非合作航天器在轨服务研究进展[J]. 机器人,2012,34(2):242-256.
LIANG B,DU X D,LI C,et al. Advances in space robot on-orbit servicing for non-cooperative spacecraft[J]. Robot,2012 ,34(2):242-256(in Chinese).
[3] PAN H, KAPIL V. Adaptive nonlinear control for spacecraft formation flying with coupled translational and attitude dynamics[C]∥Proc. of 40th IEEE Conf. on Decision and Control.Orlando:IEEE,2001:2057-2062.
[4] STANSBERY D T,CLOUTIER J R. Position and attitude control of a spacecraft using the state-dependent Riccati equation technique[C]. The 2000 American Control Conference,Chicago,USA,28-30 July,2000. Chicago:IEEE,2000:1867-1871.
[5] WANG X,YU C. Unit dual quaternion-based feedback linearization tracking problem for attitude and position dynamics [J]. Systems & Control Letters,2013,62(3):225-233.
[6] FILIPE N,TSIOTRAS P. Adaptive position and attitude-tracking controller for satellite proximity operations using dual quaternions[J]. Journal of Guidance Control & Dynamics,2015,38(4):566-577.
[7] GUI H,VUKOVICH G. Dual-quaternion-based adaptive motion tracking of spacecraft with reduced control effort[J]. Nonlinear Dynamics,2015,83(1-2):1-18.
[8] SINGLA P,SUBBARAO K,JUNKINS J L. Adaptive output feedback control for spacecraft rendezvous and docking under measurement uncertainty[J]. Journal of Guidance Control & Dynamics,2015,29(4):892-902.
[9] SUN L,HUO W. Robust adaptive control of spacecraft proximity maneuvers under dynamic coupling and uncertainty[J]. Advances in Space Research,2015,56(10):2206-2217.
[10] 高登巍,罗建军,马卫华. 基于Lyapunov方法的非合作目标接近与视线跟踪[J]. 西北工业大学学报,2013(4):577-583.
GAO D W,LUO J J,MA W H. Approaching and tracking a maneuvering non-vooperative object using Lyapunov approach[J]. Journal of Northwestern Polytechnical University,2013(4):577-583(in Chinese).
[11] 苏晏,黎康. 近距离星间相对姿轨耦合动力学建模与控制[J]. 空间控制技术与应用,2014,40(4):20-25.
SU Y,LI K. Coupled relative attitude-orbit dynamics and control of a near satellites[J]. Aerospace Control and Application,2014,40(4):20-25(in Chinese).
[12] 靳永强,张庆展,康志宇,等. 服务航天器超近程逼近失控目标的建模与控制[J]. 中国空间科学技术,2015,32(3):1-9.
JIN Y Q,ZHANG Q Z,KANG Z Y,et al. Modeling and controlling for servicing spacecraft approaching a tumbling target in close proximity[J]. Chinese Space Science and Technology,2015,32(3):1-9(in Chinese).
[13] 李鹏,岳晓奎,袁建平. 基于θ-D方法的在轨操作相对姿轨耦合控制[J]. 中国空间科学技术, 2012, 32(4):8-14.
LI P,YUE X K,YUAN J P.Coupled control of relative position and attitude based on θ-D technique for on-orbit operations[J]. Chinese Space Science and Technology,2012,32(4):8-14(in Chinese).
[14] XIN M,PAN H. Nonlinear optimal control of spacecraft approaching a tumbling target[J]. Aerospace Science & Technology,2009,15(2):79-89.
[15] 闵颖颖,刘允刚. Barbalat引理及其在系统稳定性分析中的应用[J]. 山东大学学报(工学版),2007,37(1):51-55.
MIN Y Y,LIU Y G,Barbalat Lemma and its application in analysis of system stability[J]. Journal of Shandong University(Engineering Science),2007,37(1):51-55(in Chinese).

