考虑摩擦的空间抓捕过程碰撞动力学分析与控制

，，*

1. 西北工业大学 航天飞行动力学技术国家级重点实验室，西安 710072 2. 西北工业大学 航天学院，西安 710072

随着空间技术的不断发展，空间机器人因其低风险、低成本等特点，在大型航天器组装、故障卫星维修、空间碎片清除等任务中将发挥越来越重要的作用。空间机器人在执行空间抓捕任务时，除了与目标产生法向碰撞外，还存在切向摩擦作用，这些作用将对机器人位姿产生影响，甚至破坏机器人与目标的结构，从而导致任务失败。因此，对空间抓捕过程的动力学研究是执行空间任务的关键技术之一。但是目前的研究大多是针对碰撞进行建模，而没有考虑摩擦因素的影响[1-4]。在抓捕目标的过程中，摩擦会阻碍机器人手爪和目标接触的相对运动，影响接触过程的动力学响应，从而对空间抓捕过程中的分析与精确控制有着不容忽视的影响。因此，在进行碰撞问题分析的同时，考虑摩擦因素的影响，对空间机器人抓捕目标过程中的动力学理论分析与控制具有十分重要的意义。

由于摩擦机理十分复杂，很难从数学上建立统一的模型，自16世纪Leonardo最先研究摩擦现象开始，至今已经有数十种摩擦模型[5]。文献[6-8]对空间机构关节间隙的碰撞和摩擦进行了研究，阎绍泽等[9]对多体系统间隙运动副的碰撞及摩擦建模方法进行了综述，但这些研究均未涉及空间抓捕过程中机械臂末端执行器与目标表面间的摩擦建模。Wu等[10]对空间抓捕转动目标中的接触动力学与控制进行了研究，其中摩擦力采用鬃毛摩擦模型进行建模，但是没有分析摩擦因素对抓捕过程的影响。同时，在实际应用中，鬃毛摩擦模型的参数辨识存在困难。张海博等[11]的研究中只考虑了滑动摩擦，没有考虑粘滞摩擦的影响。

通常，摩擦模型可按照摩擦现象是否由微分方程描述分为动态摩擦模型(如鬃毛摩擦模型)和静态摩擦模型(如库伦摩擦模型)[12]。文献[5]系统地介绍了几种较为常用的摩擦模型，并对每一种模型的构成、特点和适用范围进行了详细论述。在实际应用中，静态摩擦模型参数辨识简单，但是无法描述静止状态的摩擦现象。动态摩擦模型能很好地对静止状态的摩擦现象进行建模，但是模型复杂，参数辨识非常困难。

从运动学的角度考虑，静止状态接触面切向方向可看作一个约束，通过引入约束方程，结合拉格朗日乘子建立动力学方程，从而可以求解出静摩擦力，这种方法被称为接触约束法或拉格朗日乘子法。与动态摩擦模型相比，这种方法无需考虑模型的参数辨识问题，应用简单。因此，本文结合拉格朗日乘子法和库伦模型的特点，在切向滑动状态根据库伦摩擦理论进行摩擦力建模，而在切向粘滞状态利用拉格朗日乘子法求解摩擦力。这样，既避免了动态摩擦模型参数辨识问题，又弥补了库伦理论无法对粘滞状态下摩擦力进行建模的不足。将求解得到的摩擦力与基于Hertz接触理论求得的碰撞力进行合成，作为对碰撞模型的修正，从而计算抓捕过程中的动力学响应。同时，针对抓捕完成后基座姿态的漂移问题，设计了控制器进行稳定控制。

1 空间机器人动力学模型

单臂刚性空间机器人系统的一般构型如图1所示。

其中，C0,C1,…,Cn分别表示基座和各个杆的质心位置，J1,J2,…,Jn分别代表各个关节，OI-XIYIZI为空间惯性坐标系，O-XYZ为原点在基座质心的基座固连坐标系，Oi-XiYiZi(i=1,2,…,n)分别为原点在各个关节的机械臂固连坐标系。

图1 空间机器人系统Fig.1 Space robot system

空间机器人系统总动能可写为：

(1)

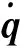
在空间微重力环境下，忽略空间机器人的重力势能，则系统的第二类拉格朗日方程为：

(2)

式中：Q为作用在系统上的广义力。

将式(1)带入式(2)，整理得：

(3)

则整个系统的动力学方程为：

(4)

2 碰撞模型

两个物体碰撞过程中既存在法向方向的碰撞力，又有切向方向的摩擦力，一般认为这两种力之间耦合作用很小，两者可以独立建模[14]。本节首先建立基于Hertz接触理论的碰撞力模型；其次，针对现有对空间抓捕碰撞过程摩擦因素考虑不足的问题，结合库伦摩擦理论和拉格朗日乘子法建立摩擦力的计算模型，作为对碰撞模型的修正，同时给出了摩擦状态转换准则及转换时刻的确定方法。

2.1 碰撞力建模

碰撞动力学的建模方法主要有冲量动量法、连续碰撞力法,以及基于连续介质力学的有限元法。其中，基于Hertz接触理论的连续碰撞力法可以得到碰撞力在碰撞期间随时间的变化规律，是研究碰撞机理的重要手段。

基于Hertz理论建立的碰撞力的表达式如下：

(5)

由式(5)可知，当碰撞物体材料属性已知，并知道嵌入深度时，则可计算出两物体之间的碰撞力。从而进一步计算出作用在机器人末端上的力和力矩，代入式(4)中，即可得到空间机器人在碰撞过程中的动力学响应结果。

2.2 考虑摩擦的修正碰撞建模

两个接触物体之间切向运动状态分为粘滞状态和滑动状态。在粘滞状态下，两物体之间的摩擦力为静摩擦力，滑动状态下接触物体之间为动摩擦力。经典库伦摩擦定律在求解滑动摩擦力时结构简单，参数辨识容易，但是无法求解静摩擦力。而在粘滞状态下，切向为一个运动学约束，利用拉格朗日乘子法可以求解静摩擦力。

因此，本文摩擦力的建模方法是：滑动状态下的动摩擦力仍采用经典库伦摩擦理论进行建模，然后与碰撞力进行矢量合成得到修正碰撞模型。而计算粘滞状态下的静摩擦力时，根据接触物体切向的运动学关系建立运动学方程，再利用拉格朗日乘子法将其与系统动力学方程联立，建立修正碰撞动力学模型。

(1)滑动状态下的摩擦力

由经典库伦摩擦理论可知，滑动状态下的摩擦力为：

Ff=-μFn

(6)

式中：μ为动摩擦系数;Fn为法向碰撞力，负号表示摩擦力与切向运动方向相反。

(2)粘滞状态下的摩擦力

当两物体处于粘滞摩擦状态时，切向可以看作一个接触约束，并且粘滞摩擦力等于接触约束力。下面推导这个约束力的计算公式。

设接触点在机械爪上用P表示，在目标上用T表示，则粘滞状态下系统的约束方程为：

Y(q,qt,t)=Pτ-Tτ=0

(7)

(8)

将式(8)代入式(7)，可得：

(9)

联立式(4)和式(9)，可以得到空间机器人在粘滞摩擦状态下的修正碰撞模型，即：

(10)

式中：Q′为作用在空间机器人上除摩擦力以外的广义力;λf为拉格朗日乘子，即静摩擦力。由式(10)，可以求解出拉格朗日乘子λf为：

(11)

(3)滑动-粘滞状态转换准则及转换时刻

两个接触物体在切向相对速度方向发生变化的时候会出现滑动-粘滞状态的转换，下面给出状态转换准则：假设在t0时刻处于粘滞状态，利用式(11)计算出粘滞摩擦力，再将其与最大静摩擦力作对比。若计算出的粘滞摩擦力小于最大静摩擦力，则该时刻状态为粘滞状态，相应的摩擦力即为粘滞静摩擦力，此时可以直接进行下一步计算；若大于最大静摩擦力，则该时刻为滑动状态，此时应按照滑动状态下摩擦力计算公式计算出动摩擦力，再进行下一步计算。状态转换准则可以简便表示如下：

式中：μs为静摩擦系数。

滑动-粘滞状态的转换发生在两物体切向相对速度为零的时刻；当相邻两个时刻切向相对速度的方向发生变化时，中间必然存在速度为零的时刻。因此，当切向相对速度发生改变时，可采用二分法，通过多次迭代，找出速度为零的时刻。

以上即为求解摩擦力的全部过程，当求解出摩擦力后，将其与第2.1节求得的碰撞力进行矢量合成，再带入式(4)，即可求解空间抓捕过程中机器人的动力学响应。图2给出了整个抓捕过程的仿真流程。

图2 抓捕过程仿真流程Fig.2 Flow chart of simulation

3 仿真验证

为了验证本文所建立的模型及相应算法，本节以图3所示的模型进行数值仿真。空间机器人由一个均质正方体基座、两个均质连杆及末端执行器构成，其几何尺寸与质量特性见表1。限于篇幅，仅考虑机器人关节锁死的情况，并假设整个抓捕过程在XOY平面内进行。

图3 抓捕初始位置示意Fig.3 Initial position for capture

物理参数基座1号杆2号杆长度/m1.001.001.00质量/kg100.0010.0010.00转动惯量Izz/(kg·m2)16.601.051.05

机器人手爪的构型如图3所示，两只机器人手爪分别由两根完全相同的刚性杆构成，每根杆的长度均为0.3 m，质量均为0.3 kg，转动惯量均为0.15 kg·m2。目标为圆柱体且轴线平行于惯性坐标系中的OZ轴，目标质量为5 kg，底面圆半径为0.15 m。机器人手爪和目标的材料均为低碳钢，其杨氏模量E1=E2=2.06×1011Pa，泊松比μ1=μ2=0.3。机器人基座在惯性坐标系中的初始位置为[0 m,0 m,0°]T，初始速度为[0 m/s,0 m/s,0(°)/s]T。机械臂初始关节角度为[30°,-30°]T，且关节角在整个抓捕过程中保持不变，即基座和两个杆可视为一个刚体。机器人手爪EA1与A1B1，EA2与A2B2之间的夹角均135°，且夹角不变。杆EA1和杆EA2相对于三号杆轴线的初始角度为[45°,-45°]，仿真开始后，两只机器人手爪分别以1 rad/s的角速度向内合拢。目标在惯性坐标系中的初始位置为[2.6 m,0.5 m,0°]T，初始速度为[-0.1 m/s,0 m/s,0(°)/s]T。

抓捕开始后，两只机器人手爪在作用于关节E上的控制力矩T的作用下逐渐合拢捕获目标，当目标被牢固捕获后，目标作用于关节E上的力矩与控制力矩T相等，抓捕结束。控制力矩为：

Ti=k×(ωr-ωzi),i=1,2

(12)

式中：k为常值系数；ωr和ωzi分别为手爪转动的期望值和实际值。

图4和图5分别为抓捕过程中空间机器人在x方向和y方向的受力情况。从图中可以看出，t=0.065 2 s，目标与机器人手爪发生第一次碰撞，0.004 s后分离；t=0.115 9 s，目标与手爪的另一端进行了第二次碰撞，0.000 4 s后又一次分离。这样反复几次，直到机器人手爪每根杆均与目标接触。此后经过多次连续碰撞，直至机器人手爪完全抓紧目标，机器人的受力变为零，抓捕过程结束。

图4 空间机器人x方向受力Fig.4 Reaction force on the x-coordinate of the space robot

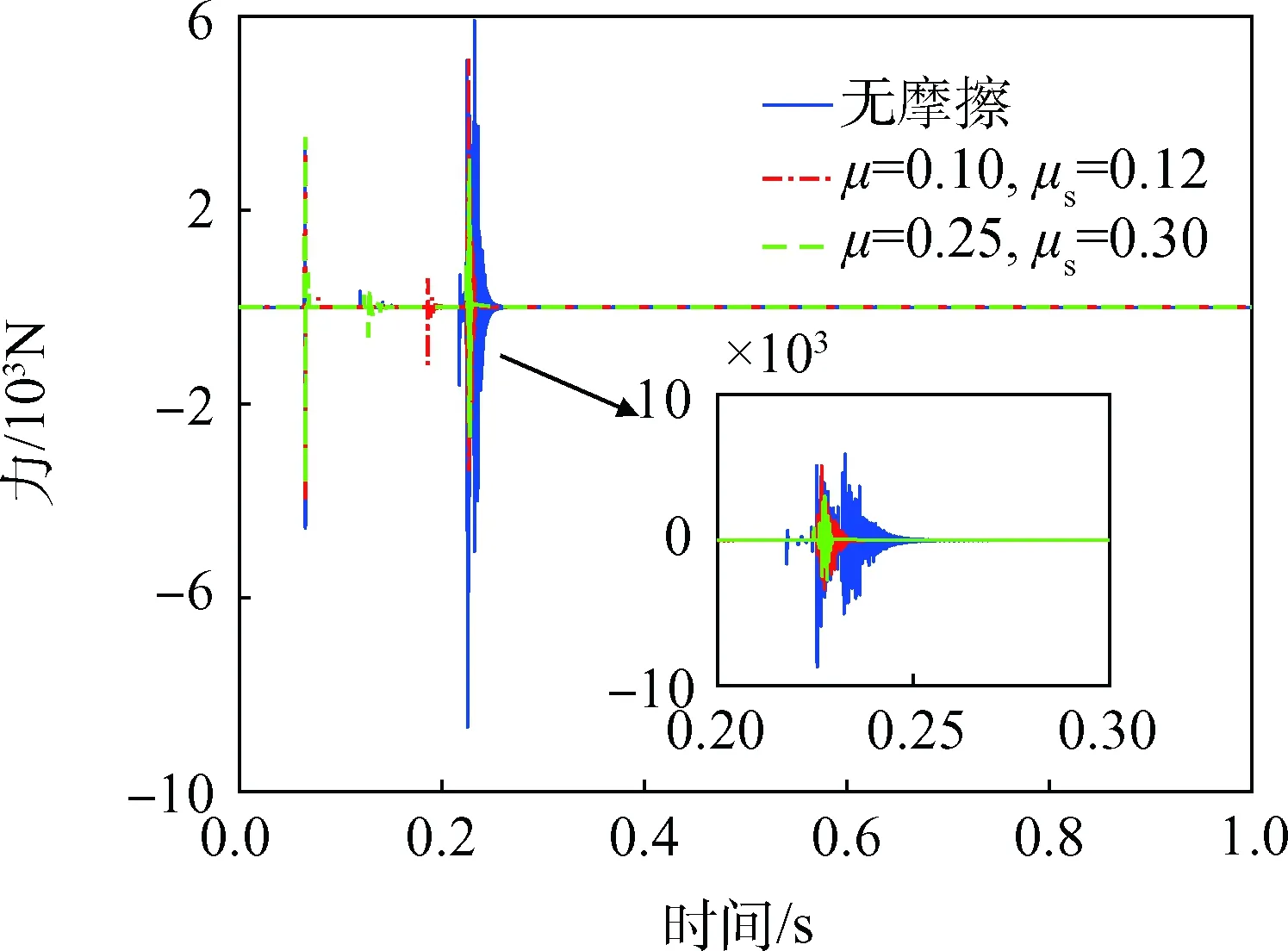
图5 空间机器人y方向受力Fig.5 Reaction force on the y-coordinate of the space robot

仿真考虑了两组摩擦因素的影响，其中μ和μs分别是动摩擦因子和静摩擦因子。由图4和图5可以看出，摩擦越大，抓捕过程中机器人的受力越小，且抓捕过程更快结束。

图6分别为机器人基座姿态角和姿态角速度的变化情况。从图中可以看出，碰撞使得姿态角速度发生复杂的变化，且摩擦越小，变化越剧烈。抓捕完成后，基座姿态角速度保持常值，使得姿态不断变大。

图7为考虑第一组摩擦时整个抓捕过程中动量和角动量的变化情况。三幅图分为为x方向、y方向线动量以及角动量的变化，其中蓝线表示机器人和目标总的动量和动量矩，红线表示机器人系统的动量和动量矩，绿线表示目标的动量和动量矩。由图中结果可以看出，碰撞发生后，机器人和目标的动量和角动量发生相应变化。由于没有外力作用，机器人和目标整体的动量和角动量守恒，仿真结果说明了所建模型的正确性。

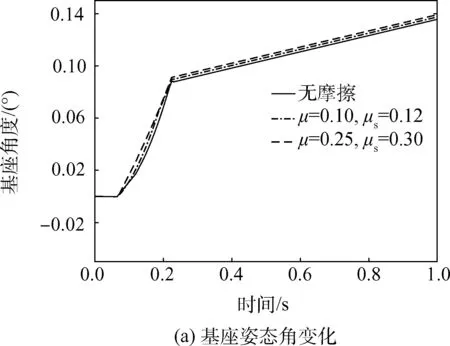
图6 基座姿态角与角速度变化Fig.6 Attitude angular and angular velocity of the base

图7 抓捕过程中的动量与角动量变化Fig.7 Linear and angular momentum in capture

由于抓捕过程中碰撞力的作用，空间机器人捕获目标后基座姿态会产生漂移，不利于后续操作。目前，针对空间机器人的姿态控制已有了大量研究[15-18]。这些文章都在传统控制方法的基础上，考虑了参数不确定等实际中可能出现的问题，结合鲁棒、自适应等理论对空间机器人控制进行了研究。然而，当空间机器人和目标参数全部已知时，这些控制就会显得复杂臃肿。基于微分几何的反馈线性化方法通过将复杂的空间机器人非线性动力学模型进行线性化处理，使得控制器的设计变得简单便捷，并可以实现各个方向的解耦控制。因此，本文基于反馈线性化的解耦控制方法，设计控制器实现对抓捕后组合体的稳定控制。组合体的动力学方程与式(4)相似：

(13)

与式(4)相比，H′和C′中包含了目标的质量特性。在机械臂关节锁死的情况下，F′为作用在基座上的控制力和控制力矩。

将式(13)写成状态空间方程的形式：

(14)

式中：u=F′为控制向量。

式(14)中的非线性存在于H′和C′中，根据反馈非线性思想，可设u=C′，此时，系统线性化为：

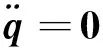
(15)

设广义坐标q的期望值为qd，偏差e=qd-q，则

u=H′v+C′

(16)

式中：

(17)

式中：kD和kP分别为微分系数矩阵和比例系数矩阵。

将式(16)代入式(14)中，可得：

(18)

可知，只要kD和kP正定，则e就可以趋于0，q就可以趋于期望值。

二阶线性系统控制器参数可由极点配置的方法确定，在实际应用中可根据具体需要配置合适的极点。本文选取了3组控制器参数，使系统分别处于欠阻尼、临界阻尼和过阻尼状态，3组控制参数分别用No.1，No.2和No.3表示，取值见表2。抓捕完成后整个系统只剩下3个自由度，所以控制器参数取为三阶对角阵。图8展示了碰撞结束后对空间机器人基座姿态进行控制后的结果。从仿真结果可以看出，碰撞结束后，在没有进行控制的情况下，机器人基座存在常值姿态角速度，姿态将会发散。而进行了控制之后，经过一段时间机器人基座姿态角速度变为零，姿态也回到原来的位置，即期望位置，这说明了所设计的控制器的有效性。而3组控制器的控制效果也各有不同，其中第1组为欠阻尼系统，响应速度最快，但控制过程会出现较大的振荡和超调。第2组相对阻尼系数接近于临界阻尼，因此响应较快，且不会出现振荡和超调。第3组在控制过程中姿态角速度的变化最小，但控制时间最长。实际应用中应根据具体情况选择控制器系数，使控制响应满足工程要求。

表2 控制器参数取值

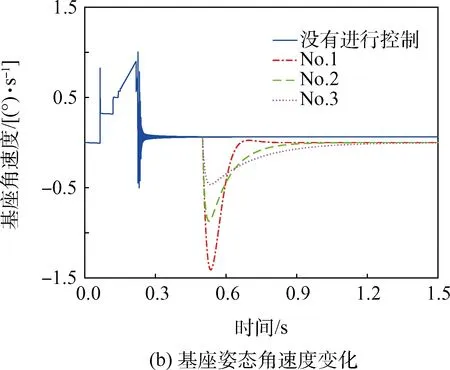
图8 基座受控与无控条件下姿态角与角速度变化Fig.8 Attitude angular and angular velocity of the base with and without controller

4 结束语

空间机器人抓捕目标过程中的碰撞动力学一直是研究热点和难点。本文主要针对空间单刚性臂机器人抓捕目标过程中的碰撞动力学进行了研究，重点是利用库伦摩擦理论和拉格朗日乘子法建立了考虑摩擦的修正碰撞模型。从仿真结果可以看出，整个碰撞过程动力学响应复杂，具有强非线性的特点；从动力学特性方面考虑，整个抓捕过程符合动量守恒；摩擦因素会造成碰撞系统的能量损失，使碰撞过程更快结束。抓捕完成后的机器人基座存在较大的姿态漂移，采用本文设计的控制器能够对漂移进行有效的稳定控制。拉格朗日乘子法能很好地弥补库伦摩擦定律对静摩擦力建模的不足，但是其数值求解比较困难，特别是多点碰撞时系统矩阵维数变化情况复杂，不利于编程仿真，如何改进其数值仿真效率，是未来的一个研究方向。

References)

[1] ZHENG Y F. Collision effects on two coordinating robots in assembly and the effect minimization[J]. Systems Man & Cybernetics IEEE Transactions on，1987，17(1)：108-116.

[2] 陈刚，贾庆轩，孙汉旭，等. 空间机器人目标捕获过程中碰撞运动分析[J]. 机器人，2010，32(3): 432-438.

CHEN G，JIA Q X，SUN H X，et al. Analysis on impact motion of space robot in the object capturing process[J]. Robot，2010，32(3)：432-438(in Chinese).

[3] SHIBLI M，AGHILI F，SU C Y. Modeling of a free-flying space robot manipulator in contact with a target satellite[C]∥Proceedings of 2005 IEEE Conference on Control Applications,28-31 August，Toronto，Canada，2005：559-564.

[4] UYAMA N，NAKANISHI H，NAGAOKA K，et al.Impedance-based contact control of a free-flying space robot with a compliant wrist for non-cooperative satellite capture[C]. IEEE/RSJ International Conference on Intelligent Robots and Systems， 7-12 October，Vilamoura，Algarve，Portugal,2012：4477-4482.

[5] 刘丽兰，刘宏昭，吴子英，等. 机械系统中摩擦模型的研究进展[J]. 力学进展，2008，38(2)：201-213.

LIU L L，LIU H Z，WU Z Y，et al. An overview of friction models in mechanical systems[J]. Advances in Mechanics，2008，38(2)：201-213(in Chinese).

[6] YANG Z，ZHENG F B. Dynamics analysis of space robot manipulator with joint clearance[J].Acta Astronautica，2011，68(7-8)：1147-1155.

[7] 阎绍泽. 航天器中含间隙机构非线性动力学问题及其研究进展[J]. 动力学与控制学报，2004，2(2)：50-54.

YAN S Z. Development and problems of nonlinear dynamics of the mechanisms with clearances for spacecrafts[J]. Journal of Dynamics and Control，2004，2(2)：50-54(in Chinese).

[8] 胡海岩，田强，张伟，等. 大型网架式可展开空间结构的非线性动力学与控制[J]. 力学进展，2013，43(4)：390-414.

HU H Y，TIAN Q，ZHANG W，et al. Nonlinear dynamics and control of large deployable space structures composed of trusses and meshes[J]. Advances in Mechanics，2013，43(4)：390-414(in Chinese)

[9] 阎绍泽，向吴维凯，黄铁球. 计及间隙的运动副和机械系统动力学的研究进展[J]. 北京大学学报(自然科学版)，2016，52(4)：741-755.

YAN S Z，XIANGWU W K，HUANG T Q. Advances in modeling of clearance joints and dynamics of mechanical systems with clearances[J]. Acta Scientiarum Naturalium Universitatis Pekinensis，2016，52(4)：741-755(in Chinese).

[10] WU S，MOU F，MA O. Contact dynamics and control of a space manipulator capturing a rotating object[C].AIAA Guidance，Navigation，and Control Conference，9-13 Febuary，Grapevine，Texas，2017：1-12.

[11] 张海博，王大轶，魏春岭. 空间机器人加注机构碰撞力建模与柔顺控制[J]. 中国空间科学技术，2015，35(4)：1-9.

ZHANG H B，WANG D Y，WEI C L. Contact dynamics model of refueling device and compliance control for space robot[J]. Chinese Space Science and Technology，2015，35(4)：1-9(in Chinese).

[12] AWREJCEWICZ J，OLEJNIK P.Analysis of dynamic sys-tems with various friction laws[J]. Applied Mechanics Reviews，2005，58(6)：389-411.

[13] 王委锋，罗建军，马卫华. 自由漂浮空间机器人动力学建模与仿真研究[J]. 科学技术与工程，2011，11(13)：3004-3008.

WANG W F，LUO J J，MA W H. Study on dynamics modeling and simulation of free-floating space robot[J]. Science Technology and Engineering，2011，11(13)：3004-3008(in Chinese).

[14] 钱震杰，章定国. 含摩擦碰撞柔性机械臂动力学研究[J]. 振动工程学报，2015，28(6)：879-886.

QIAN Z J，ZHANG D G. Frictional impact dynamics of flexible manipulator arms[J]. Journal of Vibration Engineering，2015，28(6)：879-886(in Chinese).

[15] WALKER M W，WEE L B. Adaptive control of space-based robot manipulators[J]. Robotics & Automation IEEE Transactions on，1991，7(6):828-835.

[16] 王益平，赵育善，师鹏，等. 捕获目标后组合体航天器抗干扰自适应控制[J]. 中国空间科学技术，2015，35(6)：20-28.

WANG Y P，ZHAO Y S，SHI P，et al. Adaptive control for stabilizing the coupling system with disturbance after capturing spacecraft[J]. Chinese Space Science and Technology，2015，35(6)：20-28.

[17] 陈志勇，陈力. 具有外部扰动及不确定系统参数的漂浮基空间机器人关节运动的增广鲁棒控制[J]. 空间科学学报，2010，30(3)：275-282.

CHEN Z Y，CHEN L. Robust control for space-based robot with external disturbances and uncertain parameters in joint space[J]. Space Science，2010，30(3)：275-282(in Chinese).

[18] ZHANG T，YUE X K，NING X，et al. Stabilization and parameter identification of tumbling space debris with bounded torque in postcapture[J]. Acta Astronautica，2016，123：301-309.