RLV再入神经网络自适应姿态控制器设计
,,
北京宇航系统工程研究所,北京 100076
可重复使用运载器(Reusable Launch Vehicle, RLV)再入返回跨越临近空间,面临高超声速空气动力学问题,气动特性不能精确获得;随着质量特性、高度、马赫数等飞行条件的改变,飞行器动力学特性变化显著;外界大气环境扰动会对飞行器产生干扰,这些因素给RLV再入姿态控制器的设计带来了困难和挑战[1-4]。RLV再入飞行包线大,经典的小扰动线性化方法结合增益预置设计控制器,需要进行大量的增益调参和分析,线性控制方法应用受到局限,难以满足期望的性能要求[5-7]。面向RLV稳定控制与飞行任务的鲁棒性需求,自适应姿态控制是一种期待的候选方案[8-10]。针对RLV再入过程中的未建模动态和各种不确定性干扰,抗扰动自适应控制器越来越受到重视[11-12]。
与常规运载器相比,RLV飞行动态变化范围更大[13],强耦合与非线性也更为严重,为此在非线性动态逆(Nonlinear Dynamic Inversion, NDI)控制的基础上,提出了一种基于径向基神经网络(Radical Basis Function Neural Network, RBFNN)的自适应姿态控制器设计方案。NDI控制作为一种精确反馈线性化的方法,具有解耦控制设计的优点,克服了小扰动线性化损失飞行器动态信息的缺点,但其对模型的准确性要求较高,缺乏对扰动的抑制能力[14]。而良好的泛化能力和快速的收敛速度是RBFNN的优势,并能有效地应用于控制设计中[15]。所设计的RBFNN自适应控制器(RBFNNAC)是在NDI结构上通过引入神经网络自适应控制策略,在线估计各种干扰的综合不确定性,并在控制器中进行补偿,克服了单独NDI控制对模型的依赖性,同时利用RBFNN的泛函能力使得控制器具有抗扰动的能力,保证RLV大包线再入姿态的控制性能,抑制未建模动态和外界干扰对姿态控制带来的不利影响。
1 非线性双环控制结构设计
为建立RLV无动力再入控制所用的姿态运动模型,不考虑轨迹和地球自转对姿态控制的影响,RLV再入飞行姿态运动数学模型参见文献[16]。再入过程动力学中,姿态角速率运动比姿态角运动要快,根据时标分离原理[17],将姿态角分为一组,记为慢状态Ω;将姿态角速率分为一组,记为快状态ω,飞行器所受的力矩记为M,则有:

从而有:
(1)

(2)
式中:
(3)
(4)
ff=
(5)
(6)
由式(3)~式(6)可知,气动未建模或者大气扰动引起气动升力L和侧力Y的不准确性,以及产生的未建模动态将通过fs直接反映在慢状态动态式(1)中,α,β的测量误差影响gs的准确性,进而对姿态控制产生影响。转动惯量的不准确性将在ff,gf中体现,干扰力矩直接影响快状态动态式(2)。
实现姿态角指令的跟踪,先对慢状态动态式(1)设计所需要的姿态角速率指令ωc,称为慢回路控制器;再由快状态动态式(2)设计所需要的控制力矩Μc,称为快回路控制器。快回路是慢回路的内环,在设计快、慢回路的控制增益时,需要保证快回路带宽是慢回路带宽的3~5倍,这样在综合慢回路时可以不考虑快回路动态特性,保证时标分离条件的满足。
RLV再入返回,对飞行器攻角α和倾侧角μ的跟踪控制非常重要,攻角的跟踪用于控制再入的气动热和能量管理。倾侧角μ的跟踪用于调整飞行纵程、横程,使得飞行器进入到预定的能量管理窗口。同时,为了限制机体表面的热通量需要镇定侧滑角β为零,保证飞行安全。在此,基于RBFNN分别设计慢回路与快回路自适应控制器,快回路控制器设计与慢回路控制器的设计是相同的,主要以慢回路控制器的设计为例给出控制器的设计过程。
2 RBFNN自适应控制器设计
2.1 标称控制器设计与分析
考虑慢状态动态式(1),当飞行器模型可准确获得时,基于动态逆方法设计以下慢回路控制器
(7)
式中:
e=Ωc-Ω
(8)
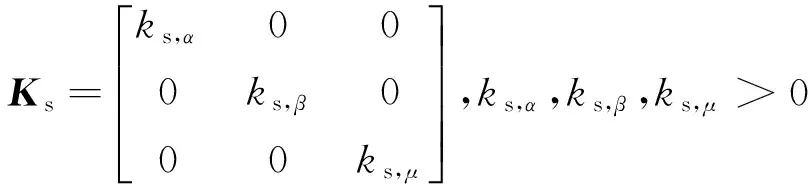
Ks为慢回路的控制带宽。
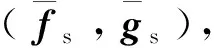
(10)
定义标称模型与真实模型的误差为:
(11)
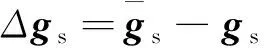
(12)
将控制律式(10)代入式(1)中,得:
(13)
由式(13)可知,模型的不准确将导致控制性能的下降。针对慢回路控制器设计,记慢回路综合的不确定项为hs,那么
(14)
同样,可以设计标称的快回路控制器。而且RLV再入过程中存在大气扰动、RCS对飞行器气动的干扰力矩以及外界的风场干扰,对于RLV快状态动态式(2),会引入干扰力矩d。此时飞行器的真实动态为:
(15)
因此,快回路控制器还需对飞行过程中的干扰力矩进行估计与补偿,消除干扰力矩的不利影响。
2.2 RBFNN自适应控制器设计
在工程实际中,飞行器动态的综合不确定项hs是未知的,为此,采用RBFNN对不确定项hs进行估计,从而在控制律中对不确定项进行补偿。
设RBFNN的输入向量、输出向量分别为x=[x1,x2,…,xn]T,Y=[y1,y2,…,yk]T,则有
Y=WTφ(x)
(16)
式中:W=[wi,j]i=1,2,…,mj=1,2,…k为神经网络输出矩阵。φ为RBFNN的节点向量,由径向基函数构成。
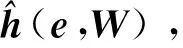
在下述2个假设条件下,RBF神经网络对连续函数在紧集范围内具有任意精度的逼近能力[18-19]。
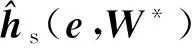
(17)
由于hs(e)有界,那么W*也是有界的,设‖W*‖F≤wmax,wmax是有界正数。设η为神经网络理想逼近误差,即
(18)
那么逼近误差η是有界的,设其界为η0,则有
(19)
在慢回路控制器设计中对不确定项hs进行补偿,设计慢回路自适应控制器为:
(20)
且
(21)
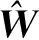
将控制器式(20)代入原系统式(1),可得:
(22)
将式(11)、式(12)代入式(22),则有:
(23)
从而有:
(24)
又由式(14),那么有:
(25)
所以
(26)
由于
(27)
则有
(28)
其中
(29)
2.3 稳定自适应律证明
通过Lyapunov方法设计自适应律和稳定性条件。对于系统慢回路,定义Lyapunov函数为:
(30)
由式(28)可知:
(31)
式中:Ks为慢回路各个通道的带宽,也是正定对称矩阵,因此存在正定矩阵P,Q满足如下Lyapunov方程:
(32)
而且
因此
(33)
将式(31)代入式(33)中,则有:
(34)
将式(32)代入式(34)中可得:
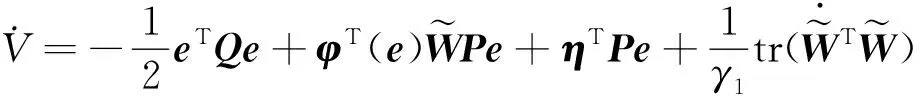
(35)
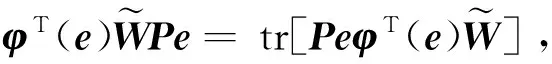
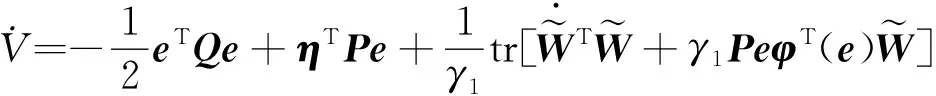
(36)
(37)
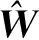
(38)
根据F-范数的性质,则有:
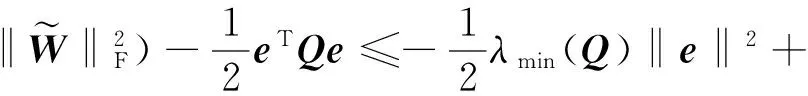
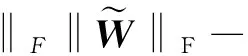
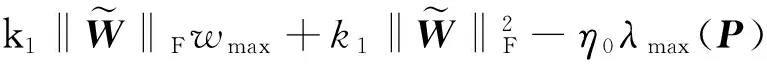
(39)
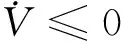
(40)
因此系统闭环收敛条件是
(41)
因此,自适应律式(37)可保证权值的有界性,解决神经网络权值的收敛问题。而且姿态角误差动态渐进稳定。从‖e‖的收敛情况可知,当Q的特征值越大,P的特征值越小,神经网络建模误差η的上界η0越小,wmax越小,则e的收敛半径越小,跟踪精度越高。
综上所述,慢回路RBFNN自适应控制器为式(20)(21),自适应律为式(37)。
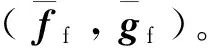
那么快回路姿态角速率误差动态的不确定项为
(42)
快回路RBFNN自适应控制器设计为
(43)
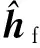
(44)
且设计快回路RBFNN自适应律为
(45)
式中:姿态角速率误差eω=ωc-ω;Kf为快回路的控制带宽,
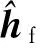
3 仿真验证
为了验证RNFNN自适应控制方案的有效性,对RLV无动力再入返回进行了仿真试验,检验其执行大包线再入的姿态控制性能和外界干扰力矩作用下的鲁棒控制性能。以下仿真算例中,姿态角速率初值为零,再入初始高度为121 km,初始速度为7 500 m/s。神经网络节点取为21个,节点中心选为0,初始化RBFNN输出矩阵为0。
3.1 大包线再入跟踪性能

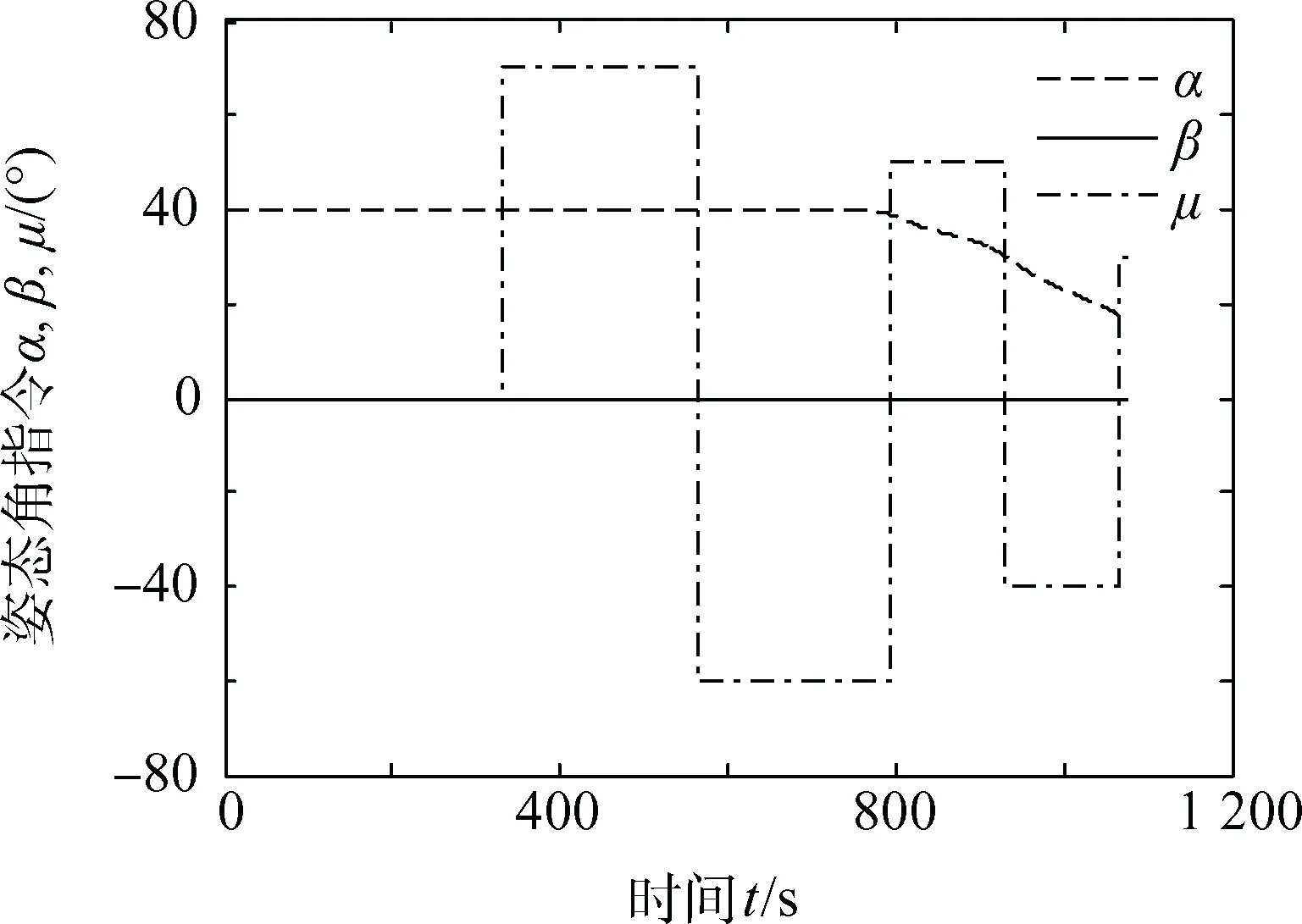
图1 姿态角指令Fig.1 Attitude command
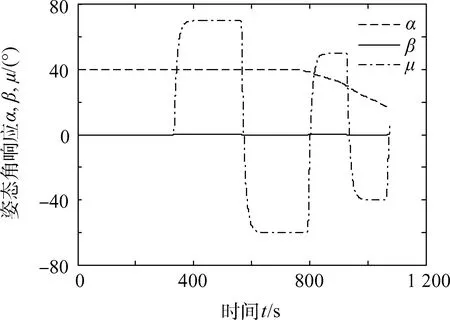
图2 姿态角响应Fig.2 Attitude response
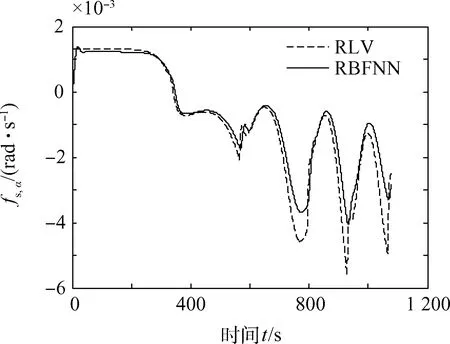
图3 RBFNN对fs,α的估计Fig.3 fs,α estimation of RBFNN
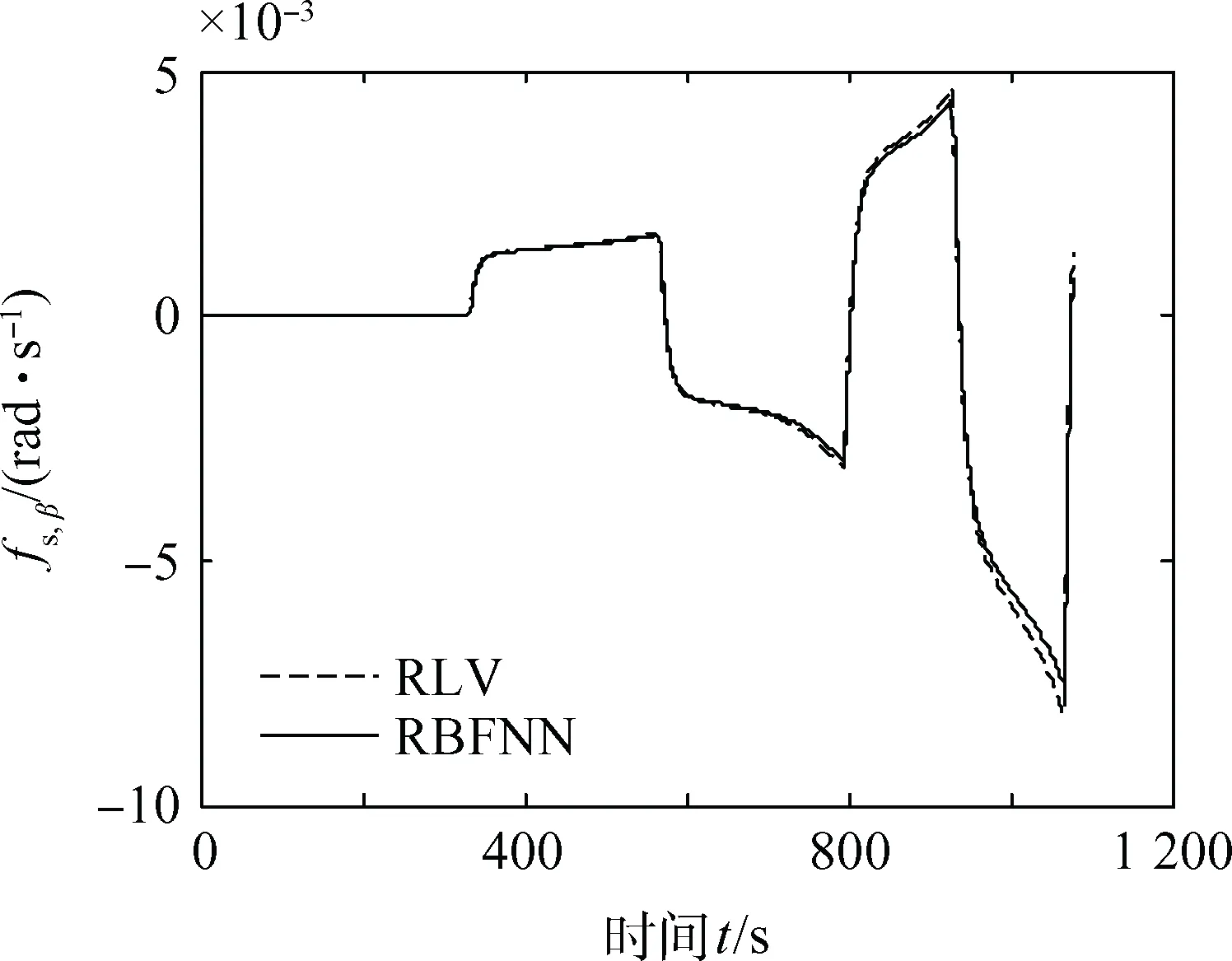
图4 RBFNN对fs,β的估计Fig.4 fs,β estimation of RBFNN

图5 RBFNN对fs,μ的估计Fig.5 fs,μ estimation of RBFNN
3.2 抗扰动抑制能力
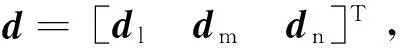
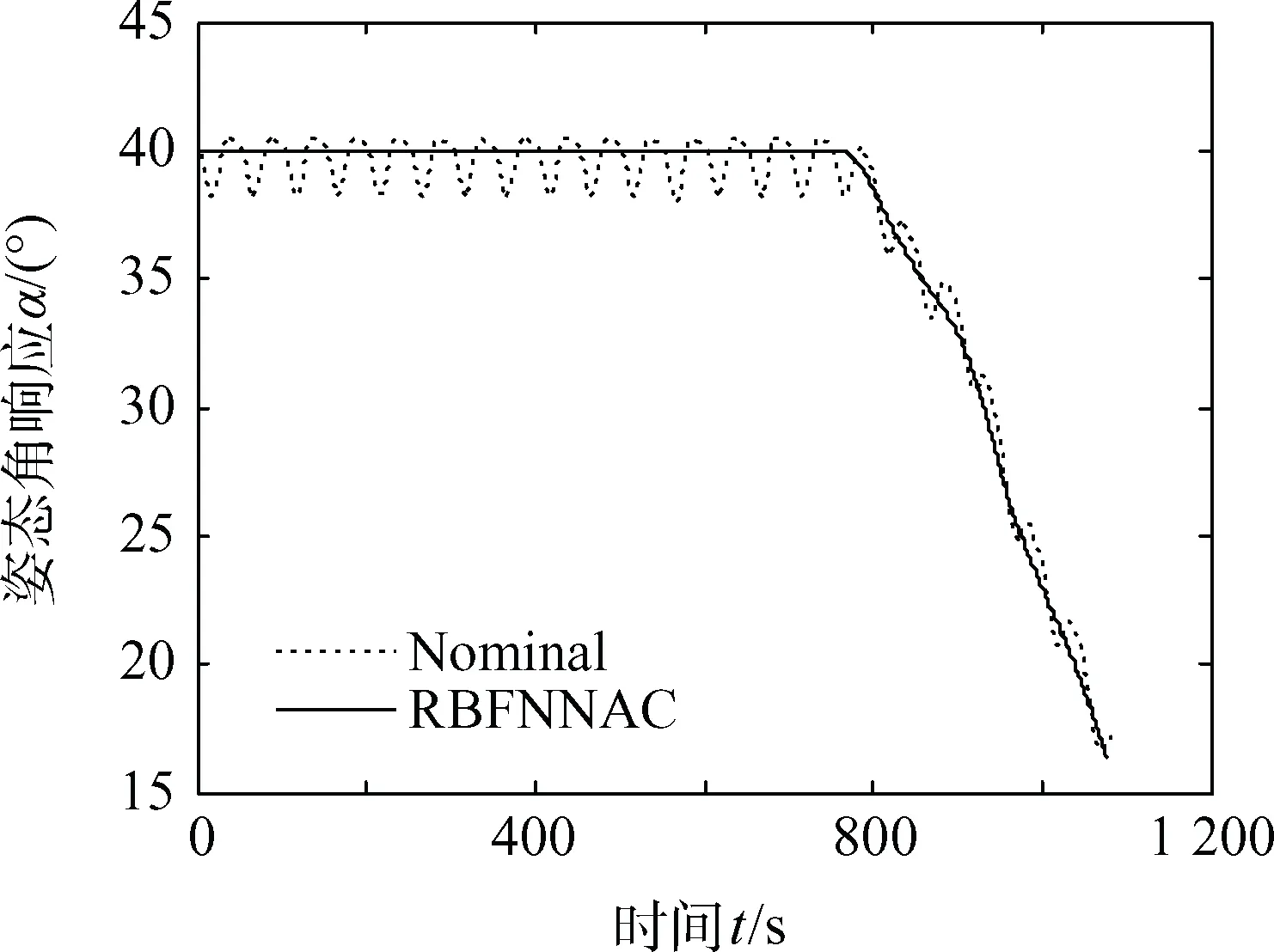
图6 姿态角α的响应Fig.6 Comparison of α response

图7 姿态角β的响应Fig.7 Comparison of β response

图8 姿态角μ的响应Fig.8 Comparison of μ response
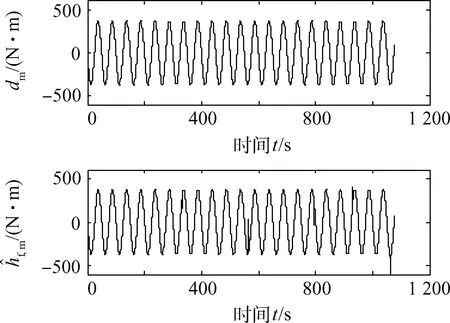
图9 RBFNN对俯仰通道干扰的估计Fig.9 dm estimation of RBFNN
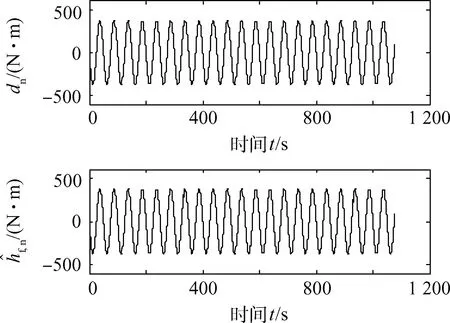
图10 RBFNN对偏航通道干扰的估计Fig.10 dn estimation of RBFNN
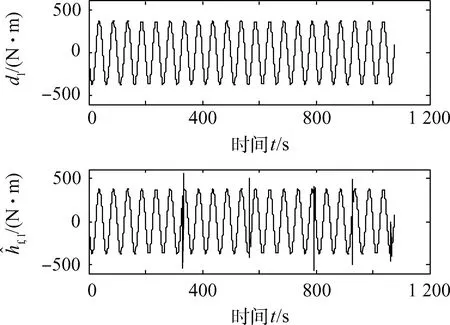
图11 RBFNN对滚转通道干扰的估计Fig.11 d1 estimation of RBFNN
4 结束语
针对RLV大包线飞行动态特性快速时变,再入飞行面临未建模动态,并受到外界干扰的影响,设计了神经网络自适应姿态控制器。所设计的自适应控制方案能够有效地完成姿态跟踪控制,满足性能指标要求。主要有如下的特点:
1)针对RLV再入返回,采用双环控制结构,分别处理内回路和外回路中的不确定性或扰动,这种分层控制结构具有补偿和抑制多种不同类型干扰的优势。
2)RBFNNAC既能够处理未建模动态带来的控制系统扰动,进行估计与补偿;又能在线估计与抑制外界干扰。控制器能够综合地处理多种干扰并存的情形,满足再入大包线控制的要求。
3)RBFNN在初始化后,根据系统闭环动态,在线自适应估计外环与内环的不确定或干扰项,内、外环RBFNN互不干扰,控制参数分别独立设计。
RBFNNAC的设计能有效地应用于RLV再入姿态控制。进一步的研究方向是,输入受限情况下自适应律修正的问题以及姿态控制器的鲁棒性评估研究。
References)
[1] 包为民. 航天飞行器控制技术研究现状与发展趋势[J]. 自动化学报, 2013, 39(6): 697-702.
BAO W M. Present situation and development tendency of aerospace control techniques[J]. Acta Automatica Sinica, 2013, 39(6): 697-702(in Chinese).
[2] 黄琳, 段志生, 杨剑影. 近空间高超声速飞行器对控制科学的挑战[J]. 控制理论与应用, 2011, 28(10): 1496-1505.
HUANG L, DUAN Z S, YANG J Y. Challenges of control science in near space hypersonic aircrafts[J]. Control Theory & Applications, 2011, 28(10): 1496-1505 (in Chinese).
[3] 吴宏鑫, 孟斌. 高超声速飞行器控制研究综述[J]. 力学进展, 2009, 39(6): 756-765.
WU H X, MENG B. Review on the control of hypersonic flight vehicles[J]. Advances in Mechanics, 2009, 39(6): 756-765 (in Chinese).
[4] HANSON J M. Advanced guidance and control project for reusable launch vehicles[C]. AIAA Guidance, Navigation, and Control Conference and Exhibit, Denver, Colorado,14-17 August, 2000: 3957.
[5] DYDEK Z T, ANNASWAMY A M, LAVRETSKY E. Adaptive control and the NASA X-15-3 flight revisited[J]. IEEE Control Systems Magazine, 2010, 30(3): 32-48.
[6] 王芳, 宗群, 田栢苓, 等. 基于鲁棒自适应反步的可重复使用飞行器再入姿态控制[J]. 控制与决策, 2014, 29(1): 12-18.
WANG F, ZONG Q, TIAN B L, et al. Robust adaptive back-stepping flight control design for reentry RLV[J]. Control and Decision, 2014, 29(1): 12-18 (in Chinese).
[7] 高清, 赵俊波, 李潜. 类HTV-2横侧向稳定性研究[J]. 宇航学报, 2014, 35(6): 657-662.
GAO Q, ZHAO J B, LI Q. Study on lateral-directional stability of HTV-2 like configuration[J]. Journal of Astronautics, 2014, 35(6): 657-662 (in Chinese).
[8] YOUNG A, CAO C Y, PATEL V, et al. Adaptive control design methodology for nonlinear-in-control systems in aircraft applications[J]. Journal of Guidance, Control, and Dynamics, 2007, 30(6): 1770-1782.
[9] JOHNSON E N, CALISE A J. Limited authority adaptive flight control for reusable launch vehicles[J]. Journal of Guidance, Concontrol, and Dynamics, 2003, 26(6): 906-913.
[10] LEE T, KIM Y. Nonlinear adaptive flight control using backstepping and neural networks controller[J]. Journal of Guidance, Control, and Dynamics, 2001, 24(4): 675-682.
[11] HAN J Q. From PID to active disturbance rejection control[J]. IEEE Transactions on Industrial Electronics, 2009, 56(3): 900-906.
[12] RAN M P, WANG Q, DONG C Y. Stabilization of a class of nonlinear systems with actuator saturation via active disturbance rejection control[J]. Automatica, 2016, 63: 302-310.
[13] 韦常柱, 琚啸哲, 张亮,等. 弹性体运载火箭及控制器设计[J]. 宇航总体技术, 2017, 1(1): 21-26.
WEI C Z, JU X Z, ZHANG L, et al. The modeling and controller design for aeroelastic rocket launcher[J]. Astronautical Systems Engineering Technology, 2017, 1(1): 21-26 (in Chinese).
[14] ITO D, GEORGIE J, VALASEK J, et al. Re-entry vehicle flight controls designs guielines: dynamic inversion,NASA/TP 2002-210771[R]. Washington D.C.:NASA, 2002.
[15] BU X Y, WU X Y, CHEN Y, et al. Nonsingular direct neural control of air-breathing hypersonic vehicle via backstepping[J]. Neurocomputing, 2015, 153(1): 164-173.
[16] 余光学, 李昭莹, 林平. 可重复使用运载器再入数学建模[J]. 中国空间科学技术, 2014,34(3): 23-31.
YU G X, LI Z Y, LIN P. RLV reentry mathematical modeling[J]. Chinese Space Science and Technology, 2014,34(3): 23-31 (in Chinese).
[17] NAIDU S D, CALISE A J. Singular perturbations and time scales in guidance and control of aerospace systems: a survey[J]. Journal of Guidance, Control, and Dynamics, 2001, 24(6): 1057-1070.
[18] PARK J, SANDBERG I W. Universal approximation using radial-basis-function networks[J]. Neural Computation, 1991, 3 (2): 246-257.
[19] 刘金琨. 智能控制[M].2版. 北京: 电子工业出版社, 2012: 186-188.
LIU J K.Intelligent control[M]. 2nd Ed. Beijing: Publishing House of Electronics Industry, 2012: 186-188(in Chinese).

