临近空间浮空器区域驻留控制策略研究

，，

深圳光启高等理工研究院 临近空间创新中心，深圳 518057

临近空间浮空器是指在海拔20～100 km之间的临近空间内飞行的浮空器[1]，其飞行高度介于常规航空器与航天器之间，具有独特的优势，可广泛应用于区域监视、侦查、数据通信与科学试验。与飞机相比，临近空间浮空器飞行高度高，覆盖范围广，滞空时间长，而且可以垂直起降；而对比于卫星，临近空间浮空器具有分辨率高、成本低、可回收等优点。随着航空航天技术的发展，美国、欧洲、日本等国家加快了对临近空间浮空器的研究与开发，谷歌公司[2]与美国国家航空航天局[3]都启动了高空气球研究计划，进行了大规模的科学载荷搭载飞行试验。

在18～24 km高度处，存在一个风速较小和温度相对稳定、基本无垂直对流的区域，该区域是目前平流层飞行器驻空的理想高度。Belmont提出零风层、弱风层的概念。它是指平流层冬夏转换期间东西风发生翻转，在东风区和西风区之间往往存在空间范围较大，时间上比较稳定的纬向风转[4]。吕达仁等提出了准零风层的概念，平流层准零风层(Quasi-Zero Wind Layer, QZWL)一般是指平流层下层20 km高度附近的大气层，上下层纬向风风向相反，同时南北风分量亦很小[5]。需要指出的是，准零风层的高度分布与地点、季节有关。

为了实现临近空间浮空器的定点驻空以及机动飞行，传统方法多选用高空螺旋桨为动力来克服水平风对于临近空间浮空器的影响，不仅增加了临近空间浮空器的系统质量，而且螺旋桨长时间工作需要消耗大量的能源，动力与能源成为制约定点实现的重要因素[6]。准零风层风场的存在为临近空间浮空器的定点驻空方法研究提供了新的方向，即改变飞行高度利用不同风向的风层实现区域驻留[7]。浮空器的高度升降控制的关键在于浮力与重力的控制，通过改变浮力与重力的大小关系就可以改变飞行高度，浮空器在飞行过程中，其浮力受热环境影响，在平流层浮空器的研究中，常考虑利用副气囊方式调节飞行高度，副气囊排气上升高度，副气囊充气降低高度。基于准零风层风场，借鉴副气囊调整高度方式，本文提出一种区域驻留方法，利用准零风层实现浮空器的东西方向控制，利用螺旋桨实现浮空器的南北方向控制，螺旋桨用来实现南北方向的控制可以有效减小螺旋桨的动力能耗。本文建立了高空气球系统的热力学模型、动力学模型，仿真验证了利用准零风层风场实现临近空间浮空器区域驻留方法的有效性。

1 高空气球系统的数学模型

高空气球系统由囊体系统、载荷系统、能源系统、通信系统与螺旋桨推进系统构成，囊体系统包含主气囊与副气囊，主气囊充有浮力气体氦气，副气囊中充有空气。副气囊可以由鼓风机鼓气，也可由放气阀门放气，与外界大气进行质量交换，调节副气囊内空气质量(空气质量会影响副气囊体积及系统质量，引起净浮力变化，从而使得高空气球系统高度上升或者下降)。副气囊充气，高空气球系统会下降高度；副气囊放气，高空气球系统会上升高度。

1.1 热力学模型

高空气球是一个气体浮空器，主、副气囊中的气体体积会受到热环境影响。假设高空气球内的氦气与空气都满足气体理想状态方程，则有

(1)

式中：P为气体压强；m为气体质量；R为气体常数；T为气体温度；V为气体体积；下标he表示主气囊中的氦气；下标air表示副气囊中的空气。

高空气球总体积为主氦气囊与副空气囊体积之和，主、副气囊通过隔膜传递压力作用，可以认为主气囊压力与副气囊压力保持平衡，即有

(2)

式中：VT为高空气球总体积；Pref为外界大气压；ΔP为囊体内部与外界大气压之间的压差。

高空气球系统球体体积与体内气体温度有关，需要建立高空气球的热力学模型。高空气球的热传递过程分为囊体、氦气与空气3个主体，囊体受热包括外界辐射，与大气换热，与氦气换热，与空气换热；氦气受热包括与囊体换热，与空气换热；空气受热包括与囊体换热，与氦气换热。带有副气囊的高空气球温度微分方程，囊体温度、氦气温度、空气温度微分方程

(3)

由温度微分方程可知，主、副气囊内气体温度变化与囊内气体质量变化有关，主气囊内氦气只在运行到工作高度或下降过程中与外界有质量交换，本文认为主气囊内氦气质量保持不变，副气囊中的空气质量变化包括阀门排气以及鼓风机吸气，则氦气与空气的质量变化可以表示为：

(4)

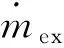
(5)

式中：ρ为气体密度；Gin为鼓风机吸气体积流量；c1为阀门放气系数；A1为放气阀门面积。

鼓风机向副气囊鼓气时的机械能大小与压差有关[9]：

Wb=ΔPGinηb

(6)

式中：ηb为鼓风机效率。

高空气球系统受到的主要热源有:

(1)直接太阳辐射

对直接太阳辐射的吸收包括外表面的吸收和透过蒙皮由内表面的吸收，而内表面由于多次反射的作用会提高内部的有效吸收率。假设囊体材料对太阳光的吸收率与透射率分别为α和τ，则反射率为r=1-α-τ，对太阳直接辐射的吸收为[11]：

(7)

式中：Ap为气球的照射投影面积；Isun为太阳辐射强度；τatm为大气透射率。

(2)大气散射

对于大气散射[8]：

(8)

式中：κ为大气散射经验系数，通常取0.1；As为囊体的外露面积。

(3)地球反照辐射

对地球反照辐射吸收为[11]：

(9)

式中：qalbedo=AlIsunsin (El)，El为太阳高度角，特别地，当太阳高度角小于0时，qalbedo=0，Al为地面平均反照率，与当地气象条件有关，一般取0.3；VF为气球表面对地球表面的角系数，与高度有关。

(4)地面红外辐射

地面红外辐射强度由斯特潘·波尔茨曼定理计算[12]：

(10)

(5)囊体的红外辐射

囊体的内外表面均向外辐射热量，内表面辐射的热量会有部分被囊体吸收，故囊体的红外辐射包括囊体吸收的红外辐射以及囊体对外的红外辐射[13]。

(11)

式中：ε为囊体的红外发射率，假设满足基尔霍夫定理，红外发射率与红外吸收率相等。

(6)大气红外辐射

大气红外辐射计算如下[13]：

(12)

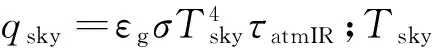
(7)对流换热

对流换热包括外表面与大气环境的对流换热以及内表面与气体间的对流换热，主气囊氦气与副气囊空气之间的对流换热，对流换热的计算如下[14]：

(13)

式中：HC为对流换热系数，可由经验公式获得；A为有效对流面积，可由气球几何模型推导；ref-film，film-he，film-air，he-air分别表示大气与囊体，囊体与氦气，囊体与空气，氦气与空气。

由热源分析结果可以得出，囊体、氦气、空气囊中空气吸收的热量为：

(14)

1.2 动力学模型

高空气球系统在飞行过程中，受到的主要作用力为浮力、系统重力、附加惯性力、气动力以及螺旋桨控制力，其受姿态影响比较小，故可以忽略高空气球系统的姿态变化，将整个系统视为质点，建立质点动力学方程。定义东北天方向为地面惯性坐标系的x，y，z正向，即向东为x正向，向北为y正向，向上为z正向。

高空气球系统竖直方向靠净浮力上升，水平面东西方向随风飘浮运动，南北方向还受到螺旋桨控制力作用:

(15)

式中：mall为系统总质量，包含氦气质量与变化的副气囊空气质量；B为浮力；g为当地重力加速度，Fdx、Fdy、Fdz为3个方向的气动力；Faddx、Faddy、Faddz为3个方向的附加惯性力；Fcy为南北方向螺旋桨控制力。

浮力大小与空气密度、气体体积、重力加速度有关：

B=ρrefVTg

(16)

式中：ρref为空气密度；VT为总体积，由热力学模型获得。

阻力大小与空气密度、风速相对速度、阻力系数、相对参考面积有关，临近空间垂向风较小，可以忽略，则有：

(17)

式中：vrx=vx-vxwind；vry=vy-vywind；vrz=vz；vxwind与vywind分别为水平方向x，y方向风速。

高空气球系统可以视为球体，其附加惯性力为[15]:

(18)

高空气球系统的运动方程为:

(19)

2 区域驻留飞行控制策略

高空气球系统的区域驻留飞行东西方向控制是根据准零风层上下存在的纬向风转来实现的，调整高度实现东西方向控制，而南北方向控制由螺旋桨产生控制力实现。准零风层高度在20 km左右，故设置区域驻留飞行控制策略在18 km之上开始作用。

准零风层高度之下风向为西风，而准零风层高度之上风向为东风，设h0为准零风层高度(此高度随时间地点变化)，则在地面惯性坐标系中有

(20)

根据当前位置与当前纬向风向决定上升或者下降高度，当前经度大于区域驻留期望经度时，需要向西运动，而如果此时纬向风向仍是西风，需要上升高度至东风层，实现高空气球向西运动，而当当前经度小于区域驻留期望经度时，需要向东运动，而如果此时纬向风向仍是东风，需要下降高度至西风层，实现高空气球向东运动。从控制机构来说，下降高度即启动鼓风机向副气囊充气，记为cin=1，上升高度即打开阀门进行副气囊放气，记为cout=1。即东西方向控制策略为：

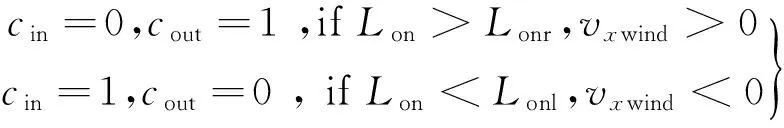
(21)

式中：Lon为当前经度；Lonr为期望驻留区域右边界经度；Lonl为期望驻留区域左边界经度。

囊体由于白天受太阳辐射的影响会出现囊体超压情况，如果此时向副气囊鼓气下降高度，会进一步增大囊体内部超压，考虑囊体安全性，应该在囊体超压大于限定值Pmax时，打开副气囊阀门进行放气，缓解囊体超压情况，即

cin=0,cout=1 , if ΔP>Pmax

(22)

风速统计规律表明，在准零风层高度附近南北方向的风速较小，南北方向区域驻留采用螺旋桨推进方案，以与期望纬度Lat0误差设计PD控制器，螺旋桨输出的控制力为：

Fcy=Kp(Lat0-Lat)+Kd(0-vy)

(23)

式中：Lat为当前纬度；Kp为比例系数；Kd为微分系数。

3 仿真结果与分析

由上述所建立的热力学与动力学模型，编写了带有副气囊的高空气球的数值仿真程序，以带有副气囊的高空气球为研究对象，仿真模拟其在国内某地的飞行过程，风场数据使用ECMWF的风场数据，由统计风场规律北纬40°左右准零风层分布时间为夏季，选择放飞时间为7月5日。高空气球囊体的热力学与辐射特性参数见表1，高空气球的基本参数见表2[11]。

表1 热力学与辐射特性参数

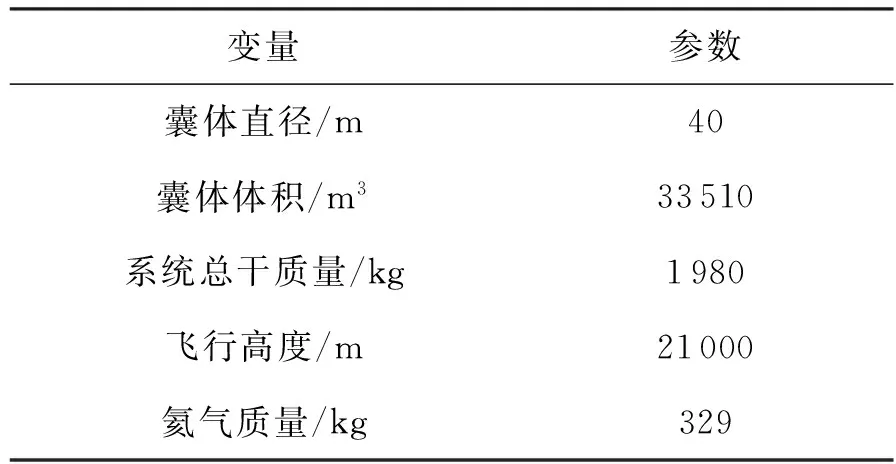
表2 高空气球基本参数

设置Lonr=87.05，Lonl=86.95，Lat0=42，Pmax=1 300 Pa，副气囊鼓风机体积流量为900 m3/h，放气阀门直径为0.3 m，取阀门系数为0.6，螺旋桨推力比例系数Kp取100，微分系数Kd取2，考虑螺旋桨推力有限，设置推力值最大值为100 N。仿真结果如图1～图5所示。

图1是放飞之后飞行过程中的飞行高度变化曲线，图2是经度变化曲线。由图2可以看出，上升过程中经过对流层风速大的区域，经度变为91.4°左右，而后区域驻留控制策略开始作用，缓慢回到经度87°左右，之后开始在87°左右振荡。可以看出，经度小于87°的时间段比大于87°时间段长。这是因为经度大于期望值时，控制策略是副气囊排气上升高度；经度小于期望值时，控制策略是副气囊充气下降高度。而放气效率远远比充气效率高，即在及时响应性能方面，上升高度比下降高度更为快速。从图1的高度变化曲线也可以看出，上升高度斜率比下降高度斜率更大。

图1 高度变化曲线Fig.1 Altitude variation of the balloon

图2 经度变化曲线Fig.2 Longitude variation of the balloon

图3是飞行过程中的纬度变化曲线，图4是飞行过程中的囊体内外压差变化曲线，图5是高空气球飞行位置变化。由图3可以看出，纬度方向，高空气球系统采用传统的PD控制方法，由于控制力的有限性以及南北方向风向的无规律性，纬度方向控制精度不高，在7天时间内控制在41°～43°之间。由图4可以看出，在飞行过程中，高空气球可能承受比较大的压差，压差出现的主要原因是受太阳辐射影响，内部气体温度升高，压强变大。超压量大小与囊体材料热力学与辐射特性参数有关，本文提出的控制策略保证了囊体内部超压在控制要求的1 300 Pa以下。由图5可以看出，除去上升阶段误差，高空气球可以在区域范围内(纬度41°～43°，经度86.5°～87.1°)实现区域驻留。

图3 纬度变化曲线Fig.3 Latitude variation of the balloon

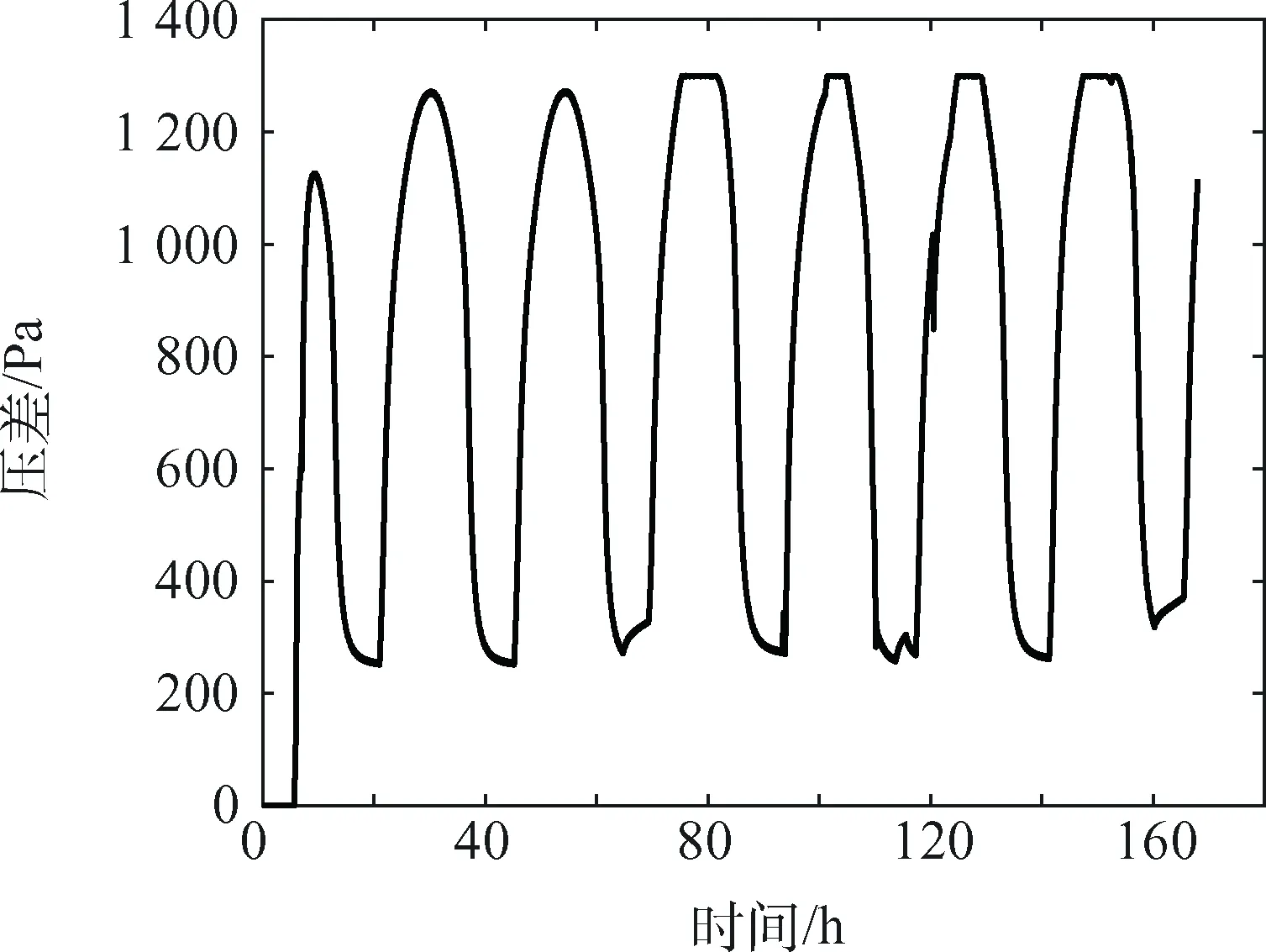
图4 压差变化曲线Fig.4 Pressure differential variation of the balloon

图5 位置变化曲线Fig.5 Location variation of the balloon

由仿真结果可以看出，上升过程经度由87°变为91.4°，而后通过西风层缓慢回到控制经度位置87°，之后在便控制在86.6°～87.1°，而南北方向，在7天时间内，纬度变化在2°之内，说明本文提出的控制策略可以实现临近空间浮空器一定时间(7天)、一定范围内(纬度2°内，经度0.5°内)的区域驻留，同时满足高空气球设置的安全超压值(小于1 300 Pa)，说明了本文提出的区域驻留控制策略的有效性。需要指出的是，由于南北方向风场的无规律性以及螺旋桨控制力的有限性，纬度方向可能一直朝一个方向运动，南北方向位置的不可控性可能会影响区域驻留控制策略的有效性。

4 结束语

本文建立了高空气球系统的动力学模型、热力学模型，结合气象统计中的准零风层风场对于高空气球的区域驻留控制策略进行了数值仿真模拟。由仿真结果可以看出，在一定时间范围内，利用副气囊充放气调节高度使得气球在不同风层运动，利用螺旋桨动力推进控制南北方向运动可以实现其在某个区域内实现大范围区域驻留。但是区域驻留方法的实现还存在副气囊充放气优化，囊体承压能力与降低超压、螺旋桨效率能源等方面问题需要加以解决。可以考虑通过进行副气囊充放气优化设计，囊体材料与热力学分析，高空螺旋桨效率优化，能源系统优化设计等手段解决，这也是下一步需要研究内容与方向。

References)

[1] 景晓龙，张建伟，黄树彩. 临近空间发展现状与关键技术研究[J] .航天制造技术，2011，4(2)：17-21.

JING X L，ZHANG J W，HUANG S C. Development actuality and key technology of near space[J]. Aerospace Manufacturing Technology，2011，4(2)： 17-21(in Chinese).

[2] 李春霖，罗蓉媛，陈彤曦. 平流层通信新思路—谷歌气球计划[J]. 通信技术，2015，48(12)：125-129.

LI C L，LUO R Y，CHEN T X. New idea for stratospheric communications—Google Loon[J].Communi-cations Technology，2015， 48(12)：125-129(in Chinese).

[3] http:∥www.nasa.gov/scientificballoons.

[4] 陶梦初，何金海，刘毅. 平流层准零风层统计特征及准两年周期振荡对其影响分析[J]. 气候与环境研究，2012，17(1):92-102.

TAO M C，HE J H，LIU Y. Analysis of the characteristics of the stratospheric quasi-zero wind layer and the effects of quasi-biennial oscillation on it[J]. Climatic and Environmental Research，2012， 17(1)：92-102(in Chinese).

[5] 吕达仁，孙宝来，李立群. 零风层与我国首次高空气球停留试验[J]. 目标与环境特性研究，2002,22(1)：45-51.

LYU D R, SUN B L, LI L Q. Zero wind layer and first dwell experiment of high-altitude balloon in China[J]. Target Environment Feat，2002,22(1)：45-51(in Chinese).

[6] 常晓飞，杨韬，符文星，等. 平流层卫星的建模与控制系统设计[J]. 哈尔滨工业大学学报，2012，44(9)：682-686.

CHANG X F，YANG T，FU W X，et al. The design of trajectory controller based on variable structure control with sliding mode for stratosphic satellite[J]. Journal of Harbin Instittute of Techanology，2012，44(9)：682-686(in Chinese).

[7] 常晓飞，白云飞，符文星，等. 基于平流层特殊风场的浮空器定点方案研究[J]. 西北工业大学学报，2014，32(1)：12-17.

CHANG X F，BAI Y F，FU W X，et al. Research on fixed-point aerostat based on its special stratosphere wind field[J]. Journal of Northwestern Polytechnical University，2014，32(1)： 12-17(in Chinese).

[8] 吕明云，巫资春. 高空气球热力学模型与上升过程仿真分析[J].北京航空航天大学学报，2011，37(5)： 505-509.

LYU M Y，WU Z C. Thermodynamic model and numerical simulation of high altitude balloon ascending process[J]. Journal of Beijing University of Aeronautics and Astronautics，2011，37(5)： 505-509(in Chinese).

[9] YAO W，LU X C，WANG C. A heat transient model for the thermal behavior prediction of stratospheric airships[J]. Applied Thermal Engineering，2014，70：380-387.

[10] 孟蒙. 基于热力学模型的平流层飞艇升降过程复合控制[D]. 上海： 上海交通大学，2013.

MENG M. Compound control for ascending and descending of stratospheric airship with thermal model[D]. Shanghai:Shanghai Jiaotong University，2013(in Chinese).

[11] ROBEITO P. A simulation model for trajectory forecast, performance analysis and aerospace mission planning with high altitude zero pressure balloons[D]. Naples：University of Naples Studies Federico II，2007.

[12] 吴耀，姚伟，王超，等. 利用自然能临近空间浮空器的热特性分析[J]. 宇航学报，2015，36(7)：784-790.

WU Y，YAO W，WANG C， et al. Thermal characteristics analysis of a near-space aerostat driven by the natural energy[J]. Journal of Astronautics，2015，36(7)：784-790(in Chinese).

[13] YANG X X，ZHANG W H，HOU Z X. Improved thermal and vertical trajectory model for performance prediction of stratospheric balloons[J]. J. Aerosp. Eng.，2015，28:04014075-1-8.

[14] 姚伟，李勇，范春石，等. 复杂环境下平流层飞艇高空驻留热动力学特性[J]. 宇航学报，2013，34(10):1309-1315.

YAO W，LI Y，FAN C S，et al. Heat dynamics behavior of a stratospheric airship in a complex thermal environment at high-altitude station-keeping conditions[J]. Journal of Astronautics，2013，34(10)：1309-1315(in Chinese).

[15] LIU Q，WU Z，ZHU M，et al. A comprehensive numerical model investigating the thermal-dynamic performance of scientific balloon[J].Advances in Space Research，2014，53：325-338.