三层直观推进概念形成—以《三角形的分类》教学为例

王婵丹

（浙江省宁波市奉化区实验小学，浙江宁波 315500）

引 言

作为“图形与几何”领域中的《三角形分类》一课，它既承担着空间与图形板块中培养学生空间观念的重任，又关注着概念理解与图形表象的关联建构。设计本课时，笔者根据学生的年龄特点与已有知识经验，将直观表象、想象操作与概念的层层建构相结合，帮助学生推理洞察图形之间的内在意义，完善认知结构。现通过课例分析，期望能成为研究“几何直观”的引玉之砖。

一、借直观操作丰富图像积累，表征数学概念

直观操作是学生学习数学有效的认识活动和学习途径。它既是手与眼的协同活动，又是手与脑的密切沟通。应用直观操作，不仅能激发学生的学习兴趣，还能使学生在感性材料的基础上加以抽象、概括，启迪学生自主建构知识，从而促进概念理解。

从实践可知，直观操作主要出现两个问题：一是所画的三角形形状单一，学生缺少大量不同形态的三角形表象积累；二是缺少从概念特征出发去画图的意识。可见，随意、简单地画个三角形并不能帮助学生把握概念本质。所以，教师在教学时既要丰富学生表象感知，又要把握概念特征将表象内化，在直观操作之前必须深化学生这两点认知[1]。于是，我们抓住图形变化的临界点再次进行了实践（如图1所示）。

图1

（一）第一层：辅“画”想象，积累表象经验

虽然画图时有了更多的条件限制，但辅以直角三角形的直观图，为学生提供一个操作支点，学生就能在操作中领悟“要画锐角三角形点C该在哪里”。此环节不仅加深了学生对概念的理解，更丰厚了图形表象。

（二）第二层：借“图”演示，沟通图形联系

动手操作后，学生已初步感知到图形之间存在一种可以互相转换的内在联系，笔者及时、有效地跟进多媒体演示，有效地引导学生用运动的眼光看图形，沟通内在联系。

生1：以直角三角形的点C为分界线，点C往上一定是锐角三角形，点C在直角三角形里面是钝角三角形。

生2：会和线段AB重合。

生3：就不能围成三角形了，三条边都重合在一起了。

第二层中借助多媒体，让静态的图形“动”起来，引导学生发现：虽然点C在不停向上运动，但锐角三角形的属性仍保持不变。一旦图形属性发生变化，图形的名称也随之改变，初步领悟到图形之间的转化是有一个分界点的。此环节不但沟通图形之间的联系，还培养学生用运动的眼光看静止的几何图形。

（三）第三层：动“点”想象，感悟分类结果

“运动的点C只能在竖的虚线上吗？想象点C在其他位置的三角形图像。”安排第三层是对前两层的补充，让学生在充分展开想象后，感悟按角分，就有这样的三类三角形，同时也提升了学生的空间观念。

操作、观察、想象，打开了学生探索与研究的闸门，在每次推进中，都引导学生将思维从动手、直观向想象、抽象过渡，从而实现对按角分的三类三角形概念理解与联系构建。

二、借直观感知达成特征交互，推进概念架构

通过实践，学生在操作中初步建立了三角形的表象，对三类三角形的概念也熟记于心。但解答“三角形中至少有几个锐角”问题时，发现正确率依然不高。究其原因，应该是探究各类三角形特征时，学生更多地关注了每类三角形的独特之处，从而忽视了它们的共性部分。为了更全面地理解概念本质，笔者安排了“截角猜三角形”的练习（如图2所示），实现直观呈现多元素材，引导学生在对比感知、分层推进中展开想象，进而深入问题核心，完善概念建构。

（一）第一层：借助直观感知，从个性拓及共性

呈现多元信息，为直观感知铺设阶梯。让空间观念较弱的学生能借助前两个判断思路和方法，展开三角形③的想象。

笔者截裁了图2中三角形③的一个锐角，然后让学生猜这个三角形是哪种。

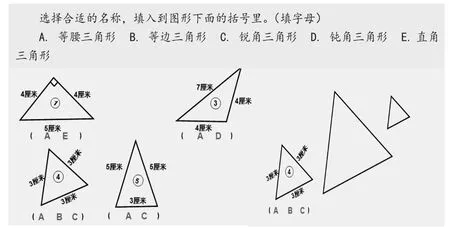
图2

生1：我猜三角形③是一个锐角三角形。

生2：错，也有可能是直角三角形、钝角三角形。

师：怎么会有那么多种情况呢？

生3：因为直角三角形和钝角三角形中也有锐角，也有可能是它们中的一个锐角露在外面，因此无法判断。

师：（问生1）你明白他的想法了吗？（生1拿起手中的三角形，演示了这一想法）

实践中，虽然有一部分学生认为③是锐角三角形，但聆听了别人思辨后，能自主地想象隐藏的部分。

在上述过程中，学生不仅能关注概念的独特之处，还能发现每类三角形都有两个锐角的共性。可见，通过直观地观察与感知已经完善了学生对三类三角形概念的理解。

（二）第二层：借助直观感知，以共性升华个性

通过第一层的想象，部分学生可能会认定，如果提供一个锐角是不能猜三角形的类别的；还有一部分学生还存在疑惑，真的不能猜了吗？此时，教师再次呈现一个锐角，立即激发了学生再次感知与探索的欲望。当出示“我是这个三角形中最大的一个角”时，将学生的“直观感知”推向了更高的境界，同时，通过合情推理与想象，在共性中发现与归纳个性特点，完善概念架构。

生：这个锐角是此三角形中最大的一个，藏在里面的那两个角一定比这个角小，那么这个三角形一定是锐角三角形。

师：你认为必须给你一个怎样的角，就一定能判断它是什么三角形？（大部分学生思考后能想到：最大的一个角。）

由此可见，“直观感知”虽是浅层次的“几何直观”，但只要教师合理开发和利用好直观素材，试着让学生主动感知发现，进而合情推理，也能从共性中发现个性特点。此时，学生在立足了“直观感知”的同时已逐步深入对图形的“直观理解”，可以说是理性认识的升华，是认识的返璞归真。

三、借直观洞察突破表象变化，深化概念本质

从边和角两个维度完整把握三角形的概念，既是本课的重点，也是发展空间观念的重要手段。我们经常安排学生观察动态的几何图形，以期打通两个维度的连接点。

在这一环节，通过“边”想象，突破图形表象的多维变化，沟通“边”与“角”的两个维度。在实践过程中，我们发现，学生在想象过程中虽然打破了存于脑子里的那个宝塔状的等腰三角形的定式表象，但他们也只能发现这个等腰三角形从角的角度看是锐角（直角、钝角）三角形，并没有完整地发现，等腰三角形可以有钝角、直角、锐角三角形这三种情况，也没有想到等边三角形，它一定是一个锐角三角形。

这就是仅停留在直观感知阶段的结果。要推进概念的进一步深化，必须在直观的基础上融入洞察和推理，借直观洞察突破表象变化，促使学生深刻理解概念本质。

（一）第一层：由“动”变“静”，搭建洞察平台

由“动态想象”变“静态描述”，多层次、多角度地帮助学生掌握概念。实践中，学生能凭借对五种三角形概念的理解，在静态的直观图中，能比较完整地理解图形之间“边”与“角”的特点。

（二）第二层：“推理”与“验证”结合，初引洞察方法

在教师的精心设问下，学生能根据作业纸上的答案（如图2所示），展开深入的思考。当他们的目光聚焦在答案上时，就能自主地感悟到“等腰三角形可以是钝角、直角、锐角三角形，但等边三角形一定是一个锐角三角形”，从而理解和感悟等腰三角形与等边三角形中的深层意义。

师：为什么图形④有这么多的名字呢？

生1问：为什么图①③⑤都有一个A呢？

生2：它们都是等腰三角形。

生3：我发现了，它们虽然都是等腰三角形，但从角的角度看，还可以是直角三角形、钝角三角形、锐角三角形。

生4：我还发现，等边三角形是特殊的等腰三角形。但它从角的角度看一定是锐角三角形，因为它每个角永远都是60°。

如果说“直观操作与感知”是建立空间观念的基础，是几何直观的初级阶段，那么“直观洞察”就是空间观念的发展与升华，是几何直观向更高层次的发展。唯有在教学中充分利用好它们相辅相成的关系，才能真正借几何直观，发展学生的空间观念。

结 语

综上所述，几何直观作为数学学习活动的一种方式，在发挥其“通过直观实现简明”的功能外，还应重视几何直观对沟通数学对象之间内在联系、展现思维活动以及发展空间观念的作用。当然，几何直观并不能独立存在，它应与感知发现、逻辑推理、直观洞察等思维活动相辅相成。在教学中只有重视了学生几何直观能力的培养，才能更好地让学生感知抽象的数学知识，更好地领悟数学知识的内涵与意义。