基于生成树的控制网最小独立异步环搜索方法研究

陈 波，高成发,管玉琦

(1.东南大学 交通学院，江苏 南京 211189；2.黑龙江省恒信测绘有限公司，黑龙江 哈尔滨 150050)

GNSS控制网异步环是指由不同步观测基线组成的闭合环，最小异步环边数及闭合差是评价控制网基线向量观测精度的重要指标。由于人工找寻异步环十分低效，故编写出计算机算法，自动搜索出所有最小独立闭合环十分重要(闭合环中除去同步环即为异步环)。目前，学者对此工作的研究主要有3个方向：基于迭代加深搜索的算法[1]、基于生成树的算法和基于Delaunay三角形的搜索算法，其中第二种方法较第一种方法搜索的闭合环的完整性更好[2]，第三种方法是一种新方法，搜索速度很快，但是完整性也得不到保障[3]。

对于基于生成树的最小闭合环搜索算法，近年来有许多学者对其进行了研究与改进，其大体思路都是先进行宽度优先搜索(或类似的算法)得到生成树，再通过添加余枝进行最短路径计算的方式得到最小独立闭合环。目前各位学者针对最小独立异步环搜索算法所发表的论文大多精讲过程中的某一部分，并且对于有些细节问题讨论的较少。实际上要完成这项工作，其过程是相当繁琐的，初学者在阅读大量文献后也不容易对此形成完备的认识。本文将对此方法原理及如何实现进行详细的阐述，包括生成树算法、最短路径搜索算法、利用生成树及最短路径搜索算法进行最小独立异步环搜索的原理及实现方法和同步环自动搜索方法，并以一个实例进行验证，以帮助初学者顺利完成这些工作。

1 生成树算法

对于一个含有n个点和m条观测基线的GNSS网(不考虑重复基线)，其独立闭合环个数为m-n+1个[4]。在闭合环搜索算法中，首先将测站视作节点，基线向量视作边(去除方向性)，把GNSS控制网看作一个由点和线(边)组成的网图。生成树算法即是在网图中建立一个“树”，该树具有以下特点：

1)连通图中所有结点；

2)不包含任何闭合环；

3)从图中任意一点均可以连通到其他所有点。

把构成该树的边称为树枝，网中剩余的边为余枝，易知余枝数为m-n+1，即为独立闭合环数。如图1所示，在网图中有一个生成树，实线为树枝，虚线为余枝。

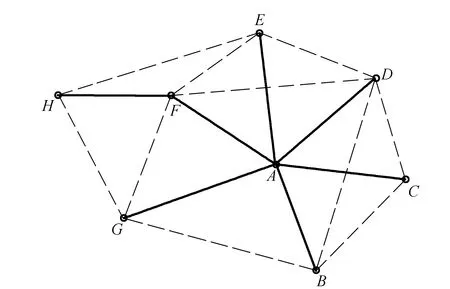
图1 生成树示意图

生成树的建立有很多种方法，这里介绍宽度优先搜索算法，其实现步骤如下：

1)为了使生成的树更为简单，首先需遍历所有边，记录下各边的两个端点，找出出现次数最多的点，该节点即为树的第一个点；

2)从树的第一个节点开始，将与该节点相连的所有边及这些边的另一个端点加入到树中；

3)从新加入的节点开始，遍历与这些节点相连的各边，如边的另一个端点不在树中，则将该边和端点加入到树中；

4)重复步骤3)，直到所有的点都在树中，则得到所需要的树。

2 最短路径—Dijkstra算法

Dijkstra算法是计算机科学中一种重要的算法，是一种典型的单源最短路径算法，其目的是计算从一个节点到网中其他所有节点的最短路径，也是基于生成树搜索最小独立闭合环过程中需要反复用到的一种算法。它是由荷兰计算机科学家Dijkstra于1959年提出的，并因此命名。其主要特点是以起始点为中心向外层层扩展，直到扩展到终点为止。

设有一个网图G，表示G中有顶点集合V和边集合E，每条边有自己的长度，图中的源点为v(即从该节点出发，计算出它到其余各节点的最短路径)，其他点为u。把网图中的顶点集合V分成两个子集合，分别是S和U，S表示已经求出最短路径(从该点到v的最短路径长度)的顶点集合，U表示其余未确定最短路径的顶点集合，一开始S中只有一个点v。S和U中每个顶点都有一个对应的长度，表示从v到u只经过S中顶点的最短路径，若只经过S中包含的顶点，从v不能到达u，则f(u)=∞。依据最短路径的长度递增次序依次把U中的顶点加入到S中，过程中保持v到S中各点的最短路径都小于v到U中任意顶点的最短路径长，直到所有的顶点都在S中。其算法步骤为：

1)一开始，S中只有节点v，S={v}，U中包含其他所有的节点，这些节点中，与v相连的u，f(u)有数值，与v不相连的u，f(u)=∞；

2)从U中选择一个f(k)最小的节点k，将节点k加入到S中，此时S中增加一个节点，U中减少一个节点；

3)以k为新的中间点，计算U中各节点u到v的距离，若从v经过节点k到节点u的距离小于原先的(此路径不经过节点k)，则将f(u)修改为新的经过节点k的距离；

4)重复步骤2)和3)，直到U为空集，此时得到源点v到网图中各节点u的最短路径。

3 搜索原理及具体步骤

利用生成树和Dijkstra算法可以进行独立闭合环的搜索，其原理是：

1)在GNSS网络中建立生成树之后，余枝的个数等于独立闭合环的个数；

2)每一条余枝的两个端点通过树(以树为网图，如图2所示)进行最小路径搜索可以得到一条路径，该路径与余枝所在的边组合即形成一个闭合环；

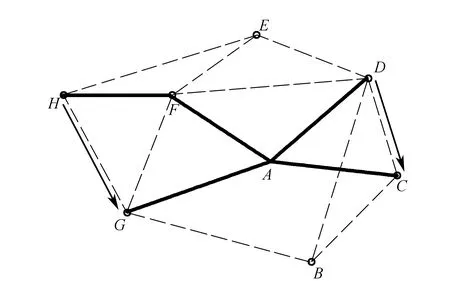
图2 以树为网图进行最小路径搜索示意图

3)由于由此得到的每一个闭合环中该余枝所在的边是别的闭合环所没有的，所以这些闭合环都是独立的。

基于以上三点，可以得到网中所有的独立闭合环，而为了得到最小独立闭合环，需要在搜索闭合环的同时对树进行扩充。同时需要指出的是，在此运用中，最短路径搜索过程中的路径的长度计算应当以边的个数代替，在边数相同时考虑路径的长度。具体步骤如下：

1)以GNSS控制网中测站为点，基线为边，建立生成树；

2)遍历所有的余枝，以每条余枝的一个端点为源点，以当前的树为网图，通过Dijkstra算法计算出该端点通过树到达该余枝的另一个端点的最短路径，与余枝本身形成闭合环；

3)找出步骤2)中得到的闭合环中最小的一个(边数最少，边数相同时长度最短者)，这个闭合环为一个最小闭合环，将其相应的余枝添加到树上，得到新的当前树，余枝数减1；

4)重复步骤2)和3)，直到余枝数为0，所有的基线都在树上，此时已经得到所有的最小独立闭合环。

这些独立闭合环中含有部分同步环，故去除掉其中属于同步环的闭合环之后，剩余的闭合环就是最小独立异步环。若考虑重复基线的影响，应当在搜索出最小独立闭合环之后，按照重复基线情况列举出所有可能的闭合环基线组合情况，再判断组合情况是否属于同步环，最终得到最小独立异步环。

4 同步环的自动搜索

对于同步环的自动搜索，目前学者对这项工作研究较少，各平差软件的说明中也未对此进行详细的描述。同步环搜索是在提取出同步观测基线的基础上进行的，本文提出一种方法，可以有效地提取出同步基线。

1)读取各基线观测的开始时刻和停止时刻，找到观测开始时刻最早的基线v1，记录下其开始时刻bt，结束时刻et。

2)遍历所有基线，判断其是否开始时刻早于et并且结束时刻晚于bt，若是，则该基线与v1是同步观测基线，记这组同步观测基线为V。

3)在遍历时进行判断，若某基线属于V，同时若其开始时刻晚于bt，则将bt修改为该基线开始时刻，若其结束时刻早于et，则将et修改为该基线结束时刻，再进行下面的遍历。

4)遍历结束即V提取完成，从此时的et往后寻找开始时间最早的基线，记录下其开始时刻bt，结束时刻et，重复上述步骤，直到所有的基线都属于某一同步观测基线组。

5 算 例

基于以上原理及方法，作者编写了计算机程序进行异步环的自动搜索，编程语言是C++，编程平台是Visual Studio 2015。计算机程序的实现思路分为以下几个部分：

1)读取基线向量文件，本文读入的是天宝公司的文件。ASC基线向量文件，对于最小独立异步环搜索工作，需要读取基线向量的起止点名、起止时刻和基线长度信息，建议以容器的方式存储数据。

3)建立生成树，通过不断以树为网进行最短路径搜索并对树进行扩充的方式搜索出所有的最小独立闭合环，具体步骤如前文所述。

4)根据重复基线情况将第3步中搜索出的闭合环，分解为不同的闭合环组合(如图3所示)。剔除掉这些闭合环组合中属于第2步搜索出的同步环的组合，即得到最小独立异步环。

图3 含重复基线闭合环分解示意图

算例数据来源于南京市玄武湖及周边地区短基线GNSS观测网，网内共有10个测站，4台接收机分5个时段观测，共有30条基线，基线平均长度在1 km左右。

观测网如图4所示，各时段观测站点如表1所示，可以看出网中共有重复基线6条(图4中加粗线段)，根据接收机数和观测时段数可以计算出最小独立闭合环数为15(基线数-重复基线数-测站数+1)，独立基线数为15。

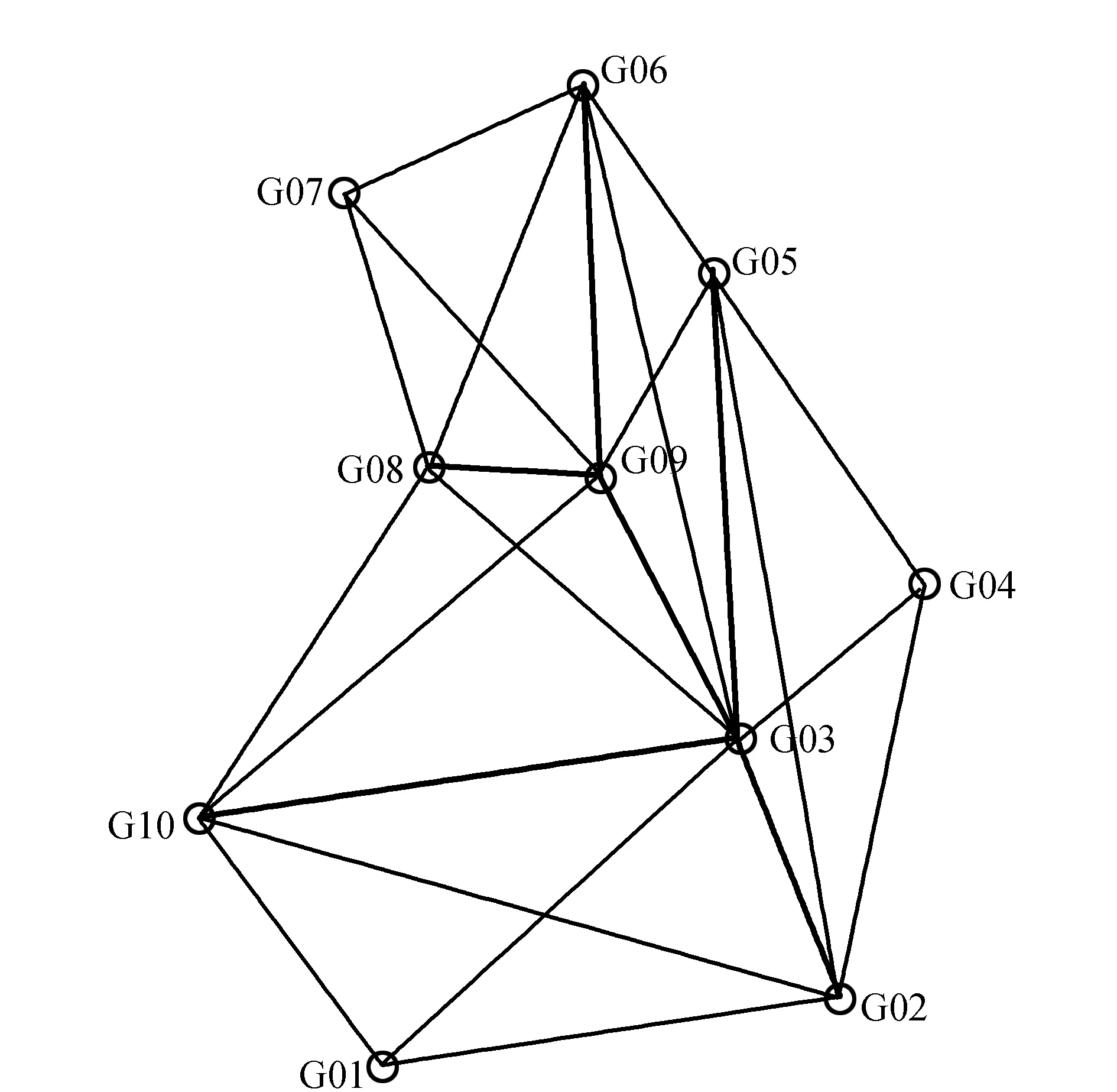
图4 观测网图

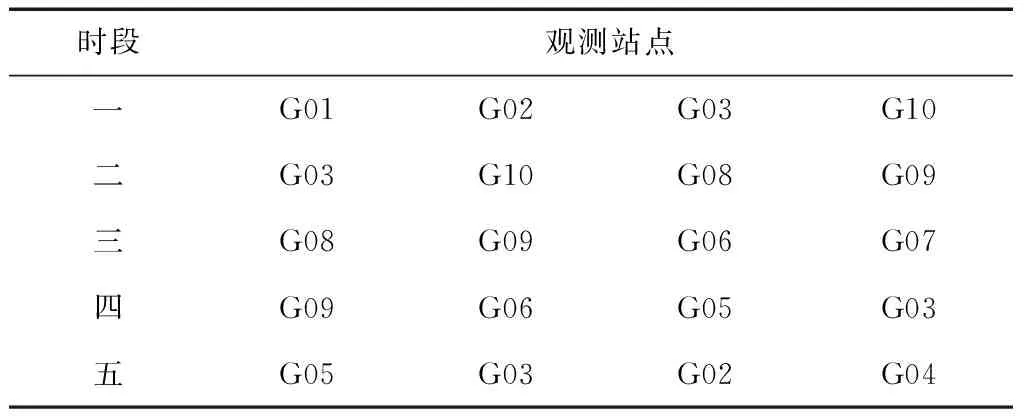
时段观测站点一G01G02G03G10二G03G10G08G09三G08G09G06G07四G09G06G05G03五G05G03G02G04

计算机程序自动搜索的同步观测环如表2所示，共有20个同步环。本算例共有5个观测时段，每个时段有4个测段，故同步环数，程序自动搜索结果完全正确。

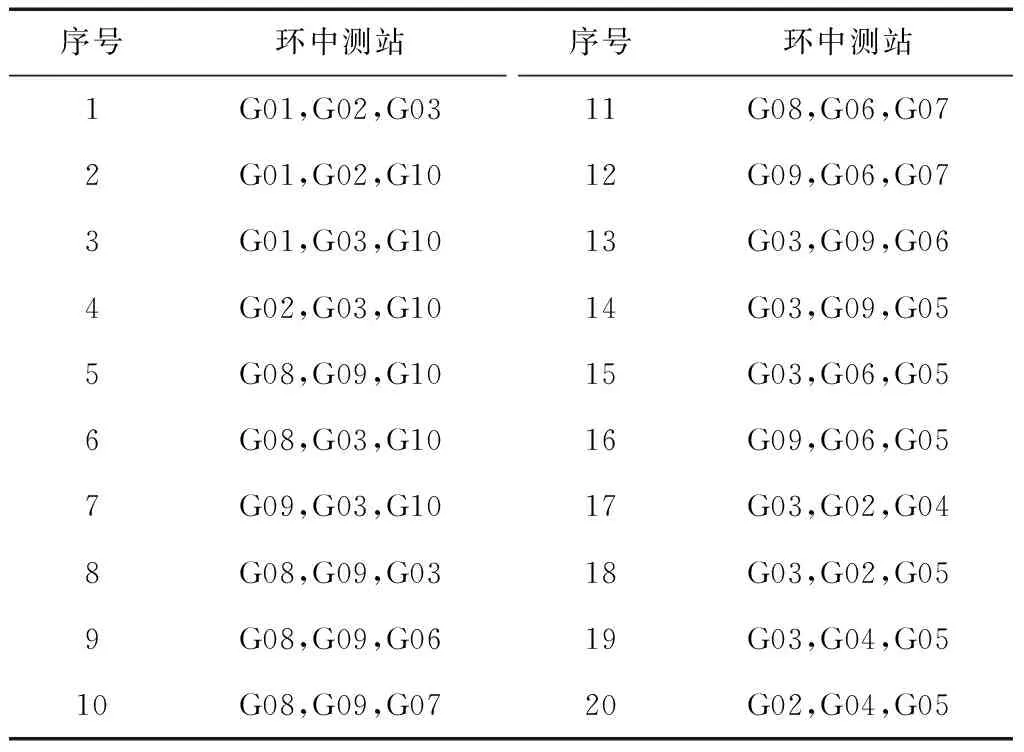
表2 同步环搜索结果

计算机程序自动搜索出的最小独立闭合环如表3所示，共有15个闭合环，观察网图可知，这些闭合环之间互相独立，且环的长度是在满足互相独立的前提下最短的。

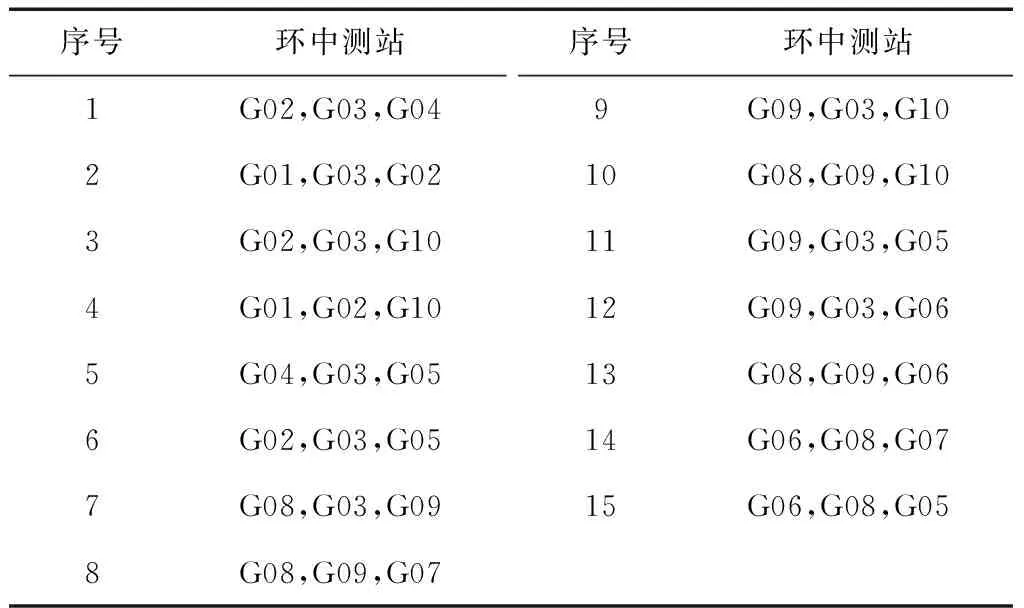
表3 最小独立闭合环搜索结果

表3中的大部分闭合环中存在重复基线(第4个和第14个闭合环中不包含重复基线，这两个闭合环属于同步观测环)，根据重复基线情况得到42种基线闭合环组合。这42种基线组合中有一部分属于表2种所列的同步观测环，除去这些同步环，可以得到27个异步环，即为最小独立异步环。至此，计算机自动搜索最小独立异步环的工作全部完成。

本算例最小独立异步环搜索结果如表4所示，表4中几个序号位于同一单元格中表示这几个异步环包含的测站相同但是包含的基线不同(由于重复基线的存在)。计算机程序运行结果如图5和图6所示，本程序为作者编写的GNSS网平差软件的一部分，图5给出的是软件读入基线向量文件之后的显示界面，图6给出的是软件自动搜索出最小独立异步环并计算对应的闭合差后的显示结果。

表4 最小独立异步环搜索结果

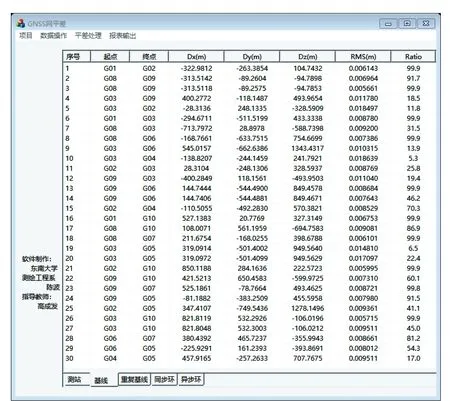
图5 计算机软件读入基线向量后的显示界面

6 结 语

本文以GNSS控制网为例，详细阐述基于生成树的控制网最小独立异步环的计算机自动搜索方法，介绍整个搜索流程中涉及的各个问题，能够帮助初学者对此项工作形成完备的认识并自主编程实现。

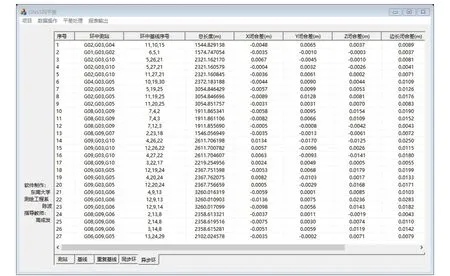
图6 计算机软件搜索最小独立异步环后显示界面

[1] 白征东. GPS网中最小独立闭合环的自动搜索[J]. 测绘科学, 1994(2):18-21.

[2] 邹进贵, 冯晨. 控制网最小独立闭合环搜索算法研究[J]. 地理空间信息, 2008, 6(6):97-99.

[3] 张西军, 张志文. 基于索引点的GPS异步环搜索算法[J]. 测绘科学, 2016, 41(6):126-129.

[4] 罗三明, 黄曲红, 王西宁,等. 控制网最小独立闭合环自动搜索算法研究[J]. 大地测量与地球动力学, 2009, 29(6):93-96.

[5] 国家测绘局测绘标准化研究所.全球定位系统(GPS)测量规范:GB/T 18314—2009[S]．北京：中国标准出版社，2009.

[6] 徐孝凯, 王凤禄. 数据结构简明教程[M]. 北京：清华大学出版社, 2005.

[7] 高成发, 胡伍生. 卫星导航定位原理与应用[M]. 北京：人民交通出版社, 2005.

[8] 陶本藻. 自由网平差[J]. 工程勘察, 1999(3):42-45.

[9] 徐昌荣, 葛山运. 基于Delaunay三角网的GPS控制网同步环和异步环自动搜索算法研究[J]. 大地测量与地球动力学, 2011, 31(1):55-58.

[10] 黄观文. GPS精密单点定位和高精度GPS基线网平差研究及其软件实现[D]. 西安：长安大学, 2008.

[11] 袁卫东. 最小生成树的算法及其应用[J]. 科学技术与工程, 2009, 9(15):4409-4412.

[12] 陈玉莹. 控制网最小独立闭合环的搜索算法[J]. 工程勘察, 2010, 38(5):65-69.

[13] 李征航. GPS测量与数据处理[M]. 武汉：武汉大学出版社, 2005.

[14] 徐昌荣, 郑俊涛, 陈艳梅. 基于边界结点的GPS控制网边界异步环自动搜索算法[J]. 测绘科学, 2012, 37(3):31-32.

[15] 王鹏磊, 刘长星, 张健,等. 基于改进的生成树和余树算法控制网最小独立闭合环搜索算法研究[J]. 大地测量与地球动力学, 2014, 34(1):113-117.