BDS伪距偏差改正对UPD估计的影响分析

徐 运，李 昕

(1.天津市测绘院,天津 300000;2.武汉大学 测绘学院,湖北 武汉 430079)

由于受到卫星端初始相位、硬件延迟、伪距观测值群延迟等因素的影响，卫星的模糊度失去整数特性，而模糊度中对应的小数部分被称为相位小数偏差(uncalibrated phase delay, UPD)[1-4]。由于UPD在一定时间范围内具有较为稳定的特性，通过对卫星UPD的估计可以修复模糊度的整周特性，从而降低精密单点定位(precise point positioning, PPP)的收敛时间，得到更加稳定可靠的结果。

与全球定位系统(global positioning system, GPS) 、格洛纳斯卫星导航系统(global navigation satellite system, GLONASS)和伽利略卫星导航系统(Galileo navigation satellite system，Galileo)不同，北斗卫星导航系统 (BeiDou navigation satellite system, BDS) 中倾斜地球同步轨道(inclined geo-synchronous orbits，IGSO)卫星和中圆地球轨道(medium Earth orbit，MEO)卫星的伪距观测值存在明显的系统偏差，该伪距偏差被证实与卫星高度角有关，对使用伪距观测值的精密定位有较为显著的影响[5-8]。文献[12]根据多路径 (multipath, MP) 序列与高度角的关系建立伪距偏差的分段线性改正模型，削弱伪距偏差的影响，提高单频精密单点定位的精度[9-12]。由于MP组合包含测站多路径和噪声等误差，各个测站的多路径和噪声水平不完全一致，文献[12]中根据多个测站的结果拟合得到的改正值不一定最优符合每一个测站，而在PPP模糊度固定方面，伪距偏差改正前后对于BDS卫星宽巷和窄巷UPD估计的影响，国内外尚无相关的系统研究与分析。针对上述问题本文首先通过多项式拟合方法对单个测站的伪距偏差进行改正，之后利用伪距偏差改正后的数据对BDS宽巷和窄巷UPD进行估计，并从数据利用率、UPD的连续性以及残差分布多个方面评估分析伪距偏差对于UPD估计的影响。

1 BDS卫星伪距偏差改正

为了分析BDS卫星的伪距偏差，常用MP组合提取伪距多路径，该多路径误差中包括伪距偏差以及观测噪声在内的偏差。MP组合主要通过单频的伪距观测值和双频的相位观测值组合得到[13]，具体表示为

(1)

式中：i,j表示不同的信号频率；MP为伪距多路径组合(m)；P,L为伪距观测值和相位观测值(m)；f对应信号的频率(HZ)；M为伪距观测值的多路径误差(m)；m为相位观测值的多路径影响；B包含相位的模糊度和信号延迟信息；ε是组合观测值的噪声。通过对一个完整弧段的MP序列去均值后，可以消去组合模糊度和信号延迟的常数部分。最终由MP组合提取得到的多路径误差也包含伪距偏差和观测噪声的影响。

图1给出香港地区连续运行参考站 (Continuously Operating Reference Stations, CORS)中HKST测站IGSO卫星和MEO卫星在B1和B2频道上的MP序列与高度角序列。可以看出，BDS的IGSO和MEO卫星的伪距多路径中存在与高度角相关的伪距偏差，且该伪距偏差并随着高度角的增大逐渐减小。

图1 BDS IGSO(C06)和MEO(C14)卫星在B1/B2频率下的MP序列与高度角序列

针对BDS伪距偏差的存在，本文利用香港CORS网中各个测站的观测数据，组成MP组合序列，根据MP序列与高度角的关系进行二次多项式拟合，得到每颗卫星(C06～C14)B1B2频率下的多项式参数，从而得到该测站每颗IGSO、MEO卫星B1和B2频率下的伪距改正值。为了验证多项式拟合改正法的有效性，计算未改正伪距偏差、多项式改正、分段线性改正[12]后MP组合观测值的均方根误差(root mean square，RMS)值，如图2所示，可以看出，改正伪距偏差后有效的提高了伪距观测值的精度，使用单站多项式拟合方法改正的结果最优。

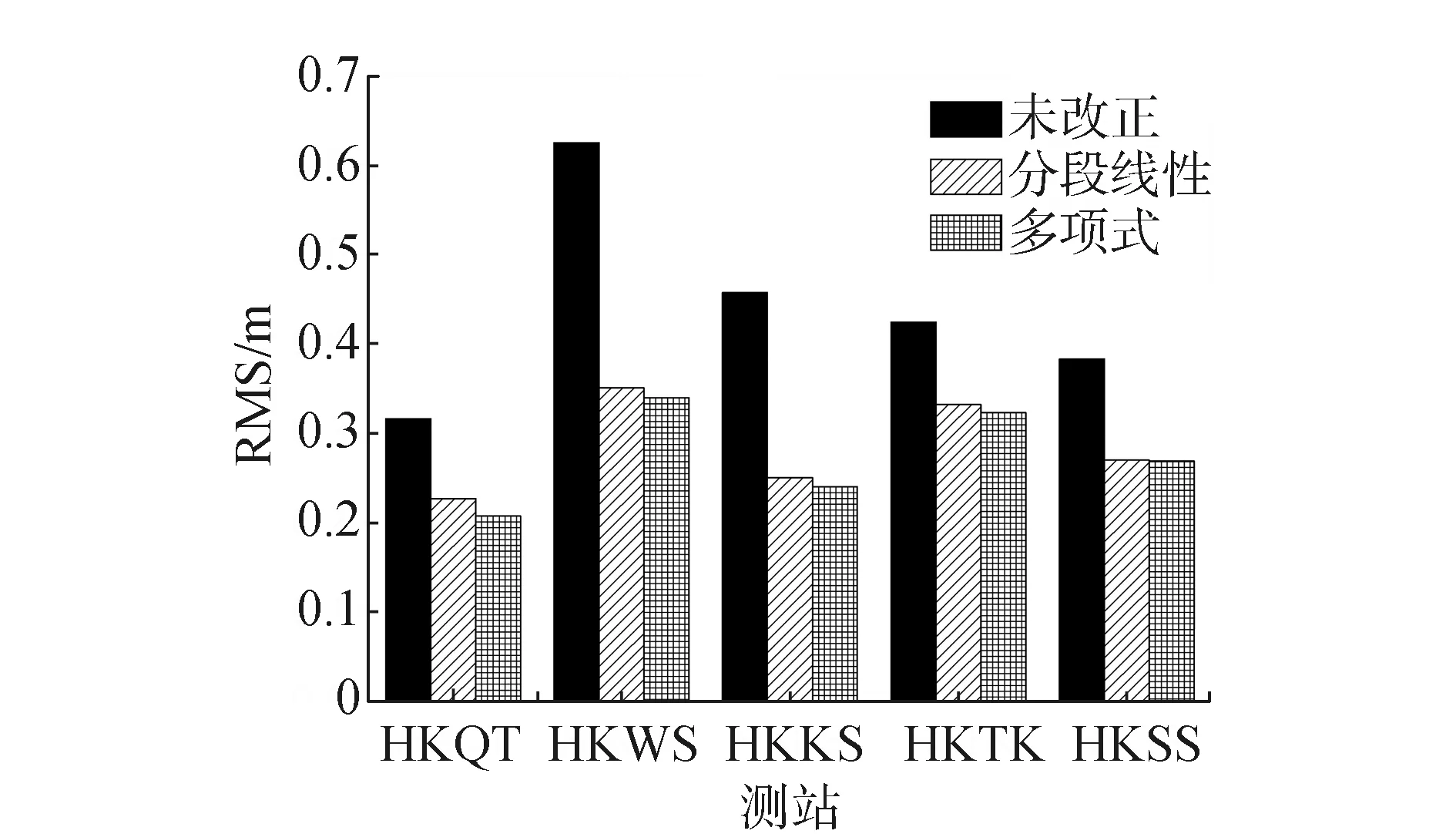
图2 CORS网不同测站伪距偏差改正前后的MP序列RMS对比

2 BDS卫星UPD估计原理与方法

对伪距观测值的伪距偏差使用多项式拟合的方法改正后，进一步进行UPD的估计。通常非差PPP模糊度固定优先固定宽巷模糊度，再通过整周宽巷模糊度和无电离层模糊度组成窄巷模糊度，最终对窄巷模糊度进行固定，其中无电离层组合与宽巷和窄巷组合的关系表示为

(2)

式中：λ对应于观测值的波长(m)；f为各观测值组合对应的频率(HZ)；N为整周模糊度的整周个数；其中下标识L1，L2表示BDS 卫星的B1和B2频率；WL和NL 分别对应于宽巷组合和窄巷组合。

实际处理过程中，由于卫星端初始相位、相位观测值信号延迟、伪距观测值群延迟等因素对模糊度参数引入常量偏差，其中小数部分破坏了模糊度的整周特性[14]。因此，在进行宽巷和窄巷模糊度的固定前需要对小数部分进行估计，将小数部分分离出去，才能正确的固定整周模糊度。为了恢复非差模糊度的整数特性，令

(3)

(4)

式中：r为接收机UPD的系数矩阵；s则对应于卫星UPD的系数矩阵。

首先通过逐历元平滑的宽巷组合(Melbourne-Wübbena，MW)得到浮点宽巷模糊度，对宽巷模糊度建立如式(4)的方程可以求得对应的接收机和卫星UPD。由于宽巷UPD 在一天范围内比较稳定，因此通常一天对每颗卫星仅估计一个值。对宽巷模糊度进行UPD改正，再通过直接取整的方法固定宽巷模糊度。

通过对区域网所有测站进行PPP解算，得到所有站的所有实数无电离层模糊度参数。

一旦获得整周宽巷模糊度和无电离层模糊度，根据式(2)可以求得浮点窄巷模糊度，对浮点窄巷模糊建立如式(4)的方程求解得到窄巷模糊度卫星端和接收机端的UPD。

值得注意的是式(4)中法方程秩亏数为1，需要引入某颗卫星或某个测站作为基准，才能将卫星端和接收机端的小数部分分离。通常选择观测卫星数目最多的测站作为基准站。

3 实验分析

3.1 BDS伪距偏差改正对宽巷UPD估计的影响

对于通过MW组合得到的浮点宽巷模糊度，伪距偏差严重时会造成超过一个整周的误差，此时会对宽巷UPD的估计产生较大的影响：①由于伪距偏差的存在无法得到正确的宽巷小数部分，在宽巷UPD的估计过程中会得到错误的估计结果。②由于偏差的存在造成估计出来的UPD残差超限而被剔除数据，降低宽巷UPD估计中的数据利用率，从而降低结果的可靠性。

图3给出2016-01-04—2016-01-13共计10 d的BDS IGSO和MEO卫星宽巷UPD估计结果，图3(a)和图3(b)是根据原始数据观测值得到的IGSO和MEO卫星的宽巷UPD结果，图3(c)和图3(d)是伪距偏差改正后IGSO和MEO的结果。可以看出，未改正BDS卫星的伪距偏差前，对于MEO卫星，不同天的宽巷UPD结果变化明显，如C14卫星，相邻两日也发生了0.5个整周的跳变，不符合宽巷UPD随时间保持稳定的特性，说明计算得到宽巷UPD值有明显的误差。而经过伪距偏差改正后，BDS卫星的宽巷UPD的波动性显著降低，保持良好的一致性，波动范围均在0.1个整周模糊度以内。改正伪距偏差前后IGSO卫星的宽巷UPD的稳定性也有提高，但不如MEO卫星明显，主要是由于IGSO卫星的伪距偏差量级较小，经过逐历元平滑后的MW组合削弱了伪距偏差的影响。同时，IGSO卫星的轨道周期是一个恒星日，不同天之间的伪距偏差具有相似的特征，从而计算得到的宽巷UPD结果也相对稳定。

UPD估计的数据利用率是衡量UPD估计内符合精度的指标之一，通常指参与估计的有效浮点宽巷模糊度所占的百分比[15]。图4给出BDS IGSO卫星和MEO卫星伪距偏差改正前后的数据利用率对比，图4上侧为伪距偏差改正前UPD估计的数据利用率，下侧为伪距偏差改正后的结果。可以看出，未改正伪距偏差时，其宽巷模糊度的数据利用率范围是57.9%～100%，平均的数据利用率是90.175%，但是其中C06和C11卫星的数据利用率仅有57.9%和81.8%；进行伪距改正后其数据利用率均值提高到98.75%。

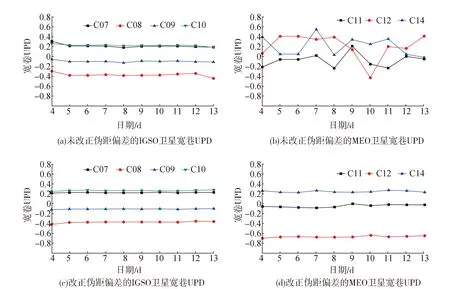
图3 伪距偏差改正前后2016-01-4—2016-01-13的宽巷UPD结果

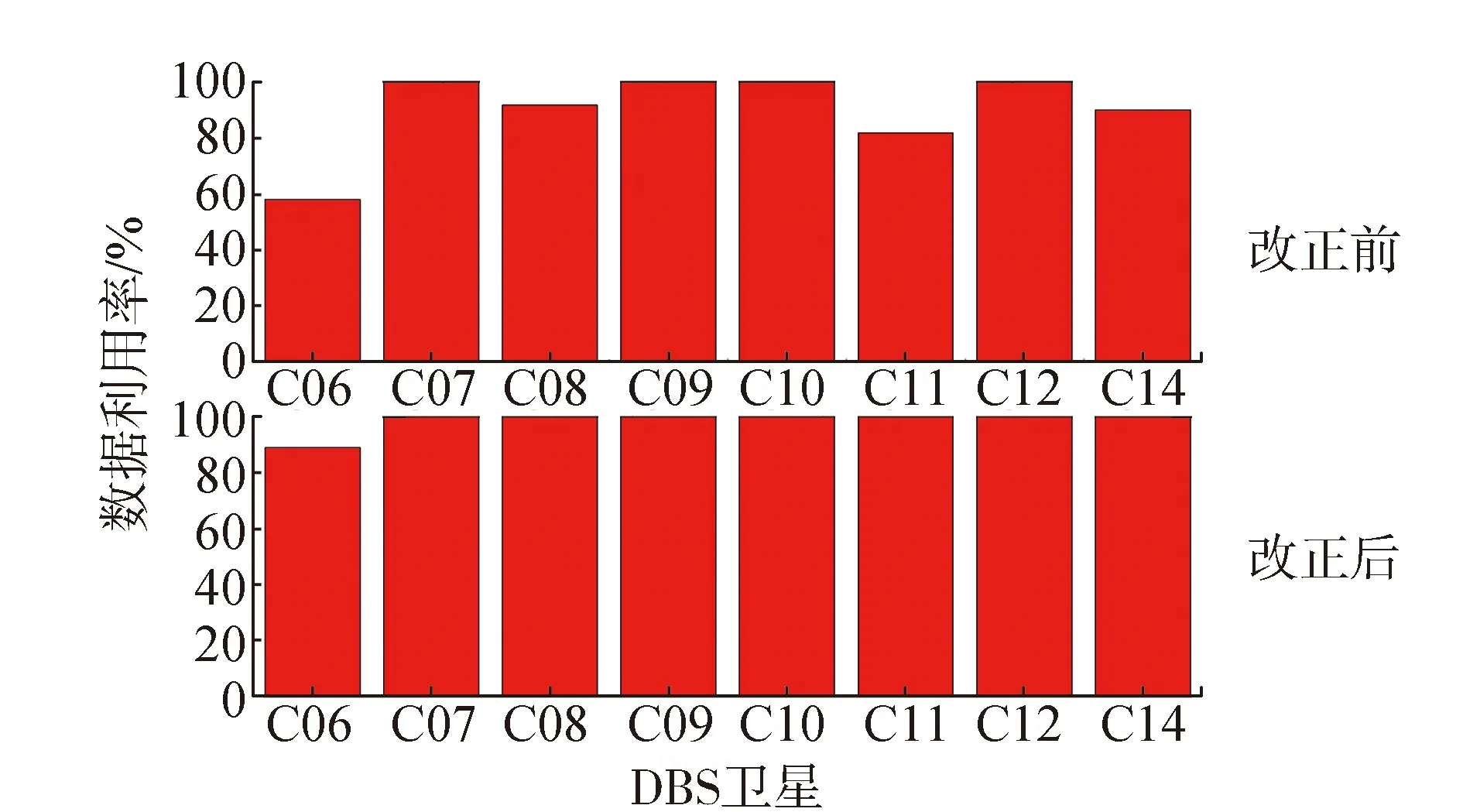
图4 伪距偏差改正前BDSIGSO和MEO卫星宽巷UPD估计的数据利用率对比

通过式(4)计算得到的验后残差也是衡量UPD的内符合精度指标之一。图5给出了所有IGSO和MEO卫星的验后残差分布图，图5(a)为伪距偏差未改正时的宽巷UPD残差分布图，其验后残差的RMS为0.098 3个整周，图5(b)为伪距偏差改正后的结果，改正后残差的RMS值降低为0.059个整周，其残差分布图也更加符合正态分布的特征。

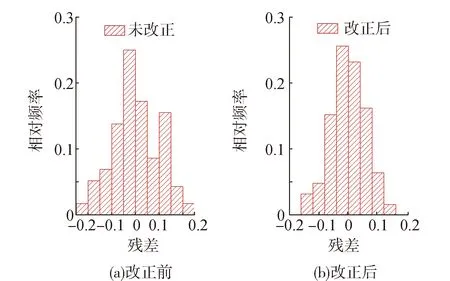
图5 伪距偏差改正前后BDS卫星宽巷UPD估计的残差分布

3.2 BDS伪距偏差对窄巷UPD估计的影响

宽巷模糊度固定后，通过无电离层组合模糊度和固定的宽巷模糊度可以求得窄巷模糊度，再根据式(4)逐历元估计窄巷UPD。为了分析BDS卫星伪距偏差对窄巷UPD的影响，本文分别使用原始观测值和伪距偏差改正后的观测值计算BDS IGSO卫星和MEO卫星的窄巷UPD并进行对比。图6给出一颗IGSO卫星(C09)和一颗MEO卫星(C11)在2016-01-05的单日窄巷UPD结果以及各个历元参与解算的有效测站数目。可以看出，伪距偏差改正前后，BDS卫星的窄巷UPD单天解的波动范围均在0.2个整周以内，伪距偏差改正之后的窄巷UPD的波动范围更小，一致性更好。未改正伪距偏差时，窄巷UPD的单历元解出现中断的情况，除了由于该卫星可视测站本身数目减小的原因，宽巷模糊度受到伪距偏差的影响造成残差超限无法固定，从而影响窄巷模糊度的可用模糊度数目，无法估计出正确的UPD值。改正伪距偏差后，窄巷的数据利用率有明显的提高，单历元的解数目增多，中断的时间较短。图7给出伪距偏差改正前后BDS IGSO和MEO卫星窄巷UPD估计的数据利用率对比，可以看出，其窄巷模糊度的数据利用率范围是68%～85%，平均的数据利用率是76.3%，其中MEO卫星的数据利用率较低不足70%；进行伪距改正后数据利用率的均值提高到84.01%。相对于宽巷UPD而言，改正伪距偏差对于窄巷UPD的精度提高有限，主要是由于窄巷UPD估计中，宽巷模糊度一旦固定，估计结果主要受到无电离层组合模糊度的影响。

图6 香港CORS网2016-01-05 C09和C11卫星伪距偏差改正前后窄巷UPD结果

图7 伪距偏差改正前后BDS卫星窄巷UPD的数据利用率对比

4 结束语

BDS IGSO和MEO卫星的伪距观测值存在与高度角相关系统偏差，对宽巷模糊度和UPD的估计产生较大的影响。本文通过多项式拟合法消除BDS伪距偏差后，利用香港地区18个CORS站2016-01-04—2016-01-13的数据估计BD SIGSO和MEO卫星的宽巷和窄巷UPD。结果表明伪距偏差改正后，BDS宽巷UPD的波动性明显降低，均在0.1个整周以内，宽巷UPD估计的平均数据利用率从90.18%提高到98.75%，验后残差的RMS值也从0.0983周降低为0.059周，残差分布更加符合正态分布的特征。伪距偏差改正之后的窄巷UPD的一致性也有所提高，平均的数据利用率由76.3%提高到84.01%。针对BDS伪距偏差对于模糊度固定的影响将是下一步研究的重点。

[1] 李星星. GNSS精密单点定位及非差模糊度快速确定方法研究[D]. 武汉：武汉大学, 2013.

[2] COLLINS P, LAHAYE F, HÉROUX P, et al. Precise point positioning with ambiguity resolution using the decoupled clock model[J]. Proceedings of International Technical Meeting of the Satellite Division of the Institute of Navigation, 2008:1315-1322.

[3] LI P, ZHANG X, REN X, et al. Generating GPS satellite fractional cycle bias for ambiguity-fixed precise point positioning[J]. Gps Solutions, 2015, 20(4):1-12.

[4] LI X, GE M, ZHANG H, et al. A method for improving uncalibrated phase delay estimation and ambiguity-fixing in real-time precise point positioning[J]. Journal of Geodesy, 2013, 87(5):405-416.

[5] 叶世榕. GPS非差相位精密单点定位理论与实现 [D]. 武汉：武汉大学, 2013.

[6] HAUSCHILD A, MONTENBRUCK O, SLEEWAEGEN J M, et al. Characterization of Compass M-1 signals[J]. GPS Solutions, 2012, 16(1):117-126.

[7] HAUSCHILD A, MONTENBRUCK O, THOELERT S, et al. A multi-technique approach for characterizing the SVN49 signal anomaly, part 1: receiver tracking and IQ constellation[J]. GPS Solutions, 2012, 16(1):19-28.

[8] MONTENBRUCK O, HAUSCHILD A, STEIGENBERGER P, et al. Three's the Challenge: A Close Look at GPS SVN62 Triple-frequency Signal Combinations Finds Carrier-phase Variations on the New L5[J]. Memórias Do Instituto Oswaldo Cruz, 2010, 82(2):259-272.

[9] MONTENBRUCK O, RIZOS C, WEBER R, et al. Getting a Grip on Multi-GNSS: The International GNSS Service MGEX Campaign[J]. Gps World, 2013, 24(2013-07):44-49.

[10] 李昕, 曾琪, 管守奎. BDS卫星伪距多路径偏差改正研究[J]. 大地测量与地球动力学, 2016, 36(8): 727-731.

[12] WANNINGER L, BEER S. BeiDou satellite-induced code pseudorange variations: diagnosis and therapy[J]. GPS Solutions, 2015, 19(4):639-648.

[13] 张小红，丁乐乐.北斗二代观测值质量分析及随机模型精化[J].武汉大学学报(信息科学版)，2013, 38(7)：832-835.

[14] LI X, GE M, ZHANG H, et al.A method for improving uncalibrated phase delay estimation and ambiguity-fixing in real-time precise point positioning. J Geod,2013,87:405-416.

[15] LI P, ZHANG X, GUO F.Ambiguity resolved precise point positioning with GPS and BeiDou. J Geod, 2016):1-16.