基于北斗三频的BDS/GPS宽巷模糊度逐级单历元固定方法
尚 睿,高成发,潘树国,陆轶材,张瑞成
(1.东南大学 交通学院,江苏 南京 210096;2.东南大学 仪器科学与工程学院,江苏 南京 210096)
2012年底,北斗二代卫星导航定位系统正式向亚太地区提供服务,作为国际上首个提供三频服务的卫星导航定位系统,北斗开启了GNSS三频定位时代[1-2]。此外,随着GPS、GLONASS的现代化以及Galileo的不断完善,多频逐渐取代双频成为GNSS的发展趋势。
利用多频GNSS信号可以构造出许多具有长波长、小噪声、弱电离层影响的线性组合观测值,极大的丰富了GNSS的解算方案[3-5]。多频GNSS模糊度解算可避开传统搜索方法的复杂计算,根据不同组合观测值的波长及误差特点,采用简单的舍入取整法逐级固定各组合模糊度,目前以TCAR和CAR为代表[6]。文献[7]得出单历元短基线三频模糊度解算成功率低的主要原因是TACR算法中第二步的宽巷模糊度很难确定。文献[8]~[9]分析认为制约中长基线三频模糊度快速解算的主要原因是残留对流层延迟,并在此基础上建立了中长基线三频模糊度解算方法。文献[10]~[11]采用部分模糊度固定方案进行BDS/GPS快速模糊度固定。文献[12]~[13]分析比较独立的超宽巷组合,采用有几何和无几何相结合的方法进行单历元模糊度固定。文献[14]分析不同大气延迟和观测值噪声对北斗宽巷模糊度解算的影响。文献[15]~[17]通过固定BDS三频宽巷实现了基于宽巷的网络RTK单历元定位。
事实上,上述实验都是基于单BDS系统或采用模拟数据进行实验验证,目前GPS、GLONASS系统播发三频信号相对较少,Galileo系统还不够完善,在一些高遮挡环境下很难利用单BDS系统实现多频解算,且由于GEO卫星带来的影响,在某些地区图形结构弱,无法实现高精度定位[18]。因此,如何充分利用BDS三频优势,提高GPS等其余星座的双频模糊度的可靠固定是进行多系统融合定位的关键。考虑到宽巷模糊度的快速解算是目前基线解算中必不可少的环节,本文充分利用BDS三频超宽巷、宽巷模糊度易于固定的优势,建立附有BDS宽巷约束的GPS宽巷解算模型,实现BDS/GPS宽巷模糊度的分层逐级单历元固定。
1 三频观测值及其组合
不失一般性,顾及双差对流层、电离层的影响,组合后的双差载波和伪距观测方程可写为[3]
Δφ(i,j,k)=Δρ+ΔT-β(i,j,k)ΔI+
λ(i,j,k)ΔN(i,j,k)+Δεφ(i,j,k),
(1)
(2)
其中载波组合观测值和伪距组合观测值分别为
(3)
(4)
载波组合观测值频率、波长和组合模糊度分别为
f(i,j,k)=i·f1+j·f2+k·f3,
(5)
(6)
(7)
电离层延迟系数为
(8)
载波观测噪声和伪距观测噪声分别为
Δ
(9)
(10)

(11)
(12)
利用北斗三频载波观测值组合,可得到一系列长波长、弱电离层、低噪声且组合系数为0的宽巷/超宽巷组合,且固定其中任意两个之后可组合得到其余模糊度固定值,典型情况如表 1所示[15]。

表1 北斗三频宽巷/超宽巷典型组合
2 宽巷模糊度固定方案
2.1 BDS/GPS宽巷模糊度固定流程
本文提出的BDS/GPS宽巷模糊度分层逐级固定方案解算方法由以下几步组成。
1)利用北斗三频观测值组合固定两个超宽巷N(0,-1,1)和N(1,4,-5),然后根据两个超宽巷组合得到BDS宽巷模糊度N(1,-1,0)。
2)利用已经固定的BDS宽巷模糊度解算基线向量信息,与GPS宽巷方程相联立,降低GPS宽巷解算模型法方程病态性,解算得到GPS双差宽巷模糊度浮点解及对应的方差—协方差矩阵,通过LAMBDA算法进行搜索,得到GPS宽巷模糊度固定解。
其解算流程如图1所示。
2.2 北斗三频超宽巷/宽巷模糊度固定
使用BDS三频求解超宽巷/宽巷时,(0,1,-1)为最优组合,(1,4,-5)和(1,3,-4)为次优组合[11],本文选取(0,1,-1)和(1,4,-5)进行超宽巷求解。

图1 BDS/GPS宽巷模糊度逐级分层解算流程
通常情况下, 采用式(13)求解超宽巷模糊度[18]。
Δ
(13)
其中,[·]为四舍五入算子。由式(13)计算得到的模糊度浮点解精度为
σ=
(14)
ΔN(1,4,-5)=
(15)
根据式(9)计算得到的浮点模糊度精度为
(16)
假定三频载波和伪距分别具有相同的精度,即
σσσσ0.01 m,
σσσσ0.5 m.
(17)
在双差条件下,假定双差电离层为10 cm,根据误差传播定律,两个超宽巷固定式子的精度分别为0.148周和0.172周,理论上超宽巷模糊度ΔN(0,-1,1)和ΔN(1,4,-5)可实现单历元固定。
当两个超宽巷模糊度固定之后,即可通过整数组合得到任一组合系数之和为0的宽巷模糊度,为满足后续模糊度解算需求,选择观测值噪声和电离层延迟较小的ΔN(1,-1,0),变换式为[18]
ΔN(1,-1,0)=-5ΔN(0,-1,1)+ΔN(1,4,-5).
(18)
2.3 北斗宽巷约束实现GPS宽巷模糊度固定
顾及电离层和对流层影响,BDS和GPS宽巷组合的定位解算方程
Δφ(1,-1,0)=Δρ+ΔT-
βΔI+λ(1,-1,0)ΔN(1,-1,0)+Δε.
(19)
当BDS宽巷模糊度固定之后,将其作为高精度约束条件,与GPS宽巷观测方程相联立
(20)
(21)
式中:AC,AG分别代表BDS和GPS基线向量系数;ΔX表示基线向量;ΔNG表示GPS宽巷模糊度;ΔNC表示已经固定的BDS宽巷模糊度;ΔLC,ΔLG分别代表BDS和GPS观测值矩阵。
对中长基线而言,利用改正模型可消除绝大部分的双差对流层延迟,式(2)中GPS宽巷模糊度浮点解解算精度主要受载波噪声和电离层延迟影响,其浮点解精度为
(22)
假定载波噪声为0.5 cm,双差电离层延迟为0.1 m,0.15 m,0.2 m,则GPS宽巷浮点解精度如表 2所示[17]。

表2 电离层延迟和载波噪声对GPS宽巷模糊度精度影响
可以看出,当电离层延迟变大的时候,若采用单历元取整GPS模糊度存在一定偏差,采用精确的BDS宽巷模型进行约束,可以准确的计算出基线向量,从而减弱GPS宽巷模糊度之间的相关性,将GPS宽巷模糊度搜索空间压缩到少数几种组合,从而利用LAMBDA算法可以搜索出正确的模糊度。
3 解算实验
为验证北斗(0,-1,1)和(1,4,-5)超宽巷组合模糊度解算精度,北斗宽巷模糊度约束GPS宽巷模糊度实现GPS宽巷模糊度单历元固定的正确性,采用南京计量院CORS长度分别为26 km和41 km两条基线进行模糊度解算实验,数据采样间隔为1 s,数据采样时间为2017-07-15 UTC时0:00—1:00;共计3 600个历元。
3.1 BDS超宽巷模糊度解算
为验证BDS超宽巷模糊度单历元取整固定的正确性,计算两条基线上BDS每颗卫星单历元超宽巷模糊度取整偏差,偏差结果如图2—图5所示(图中C代表BDS卫星,C后数字代表卫星PRN编号)。

图2 基线JNNF-LHNF (0,-1,1)组合模糊度偏差
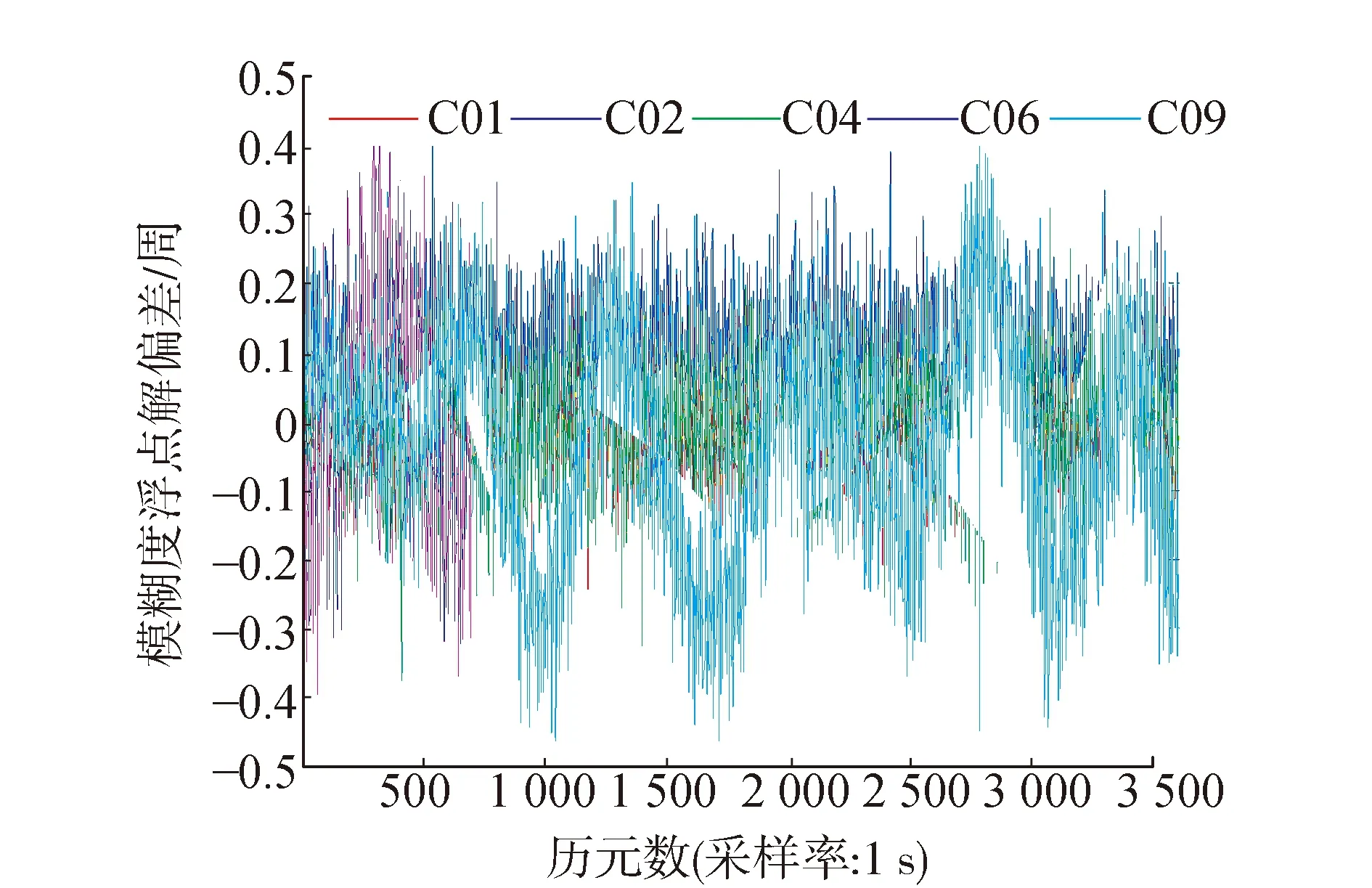
图3 基线JNNF-LHNF N(1,4,-5)组合模糊度偏差
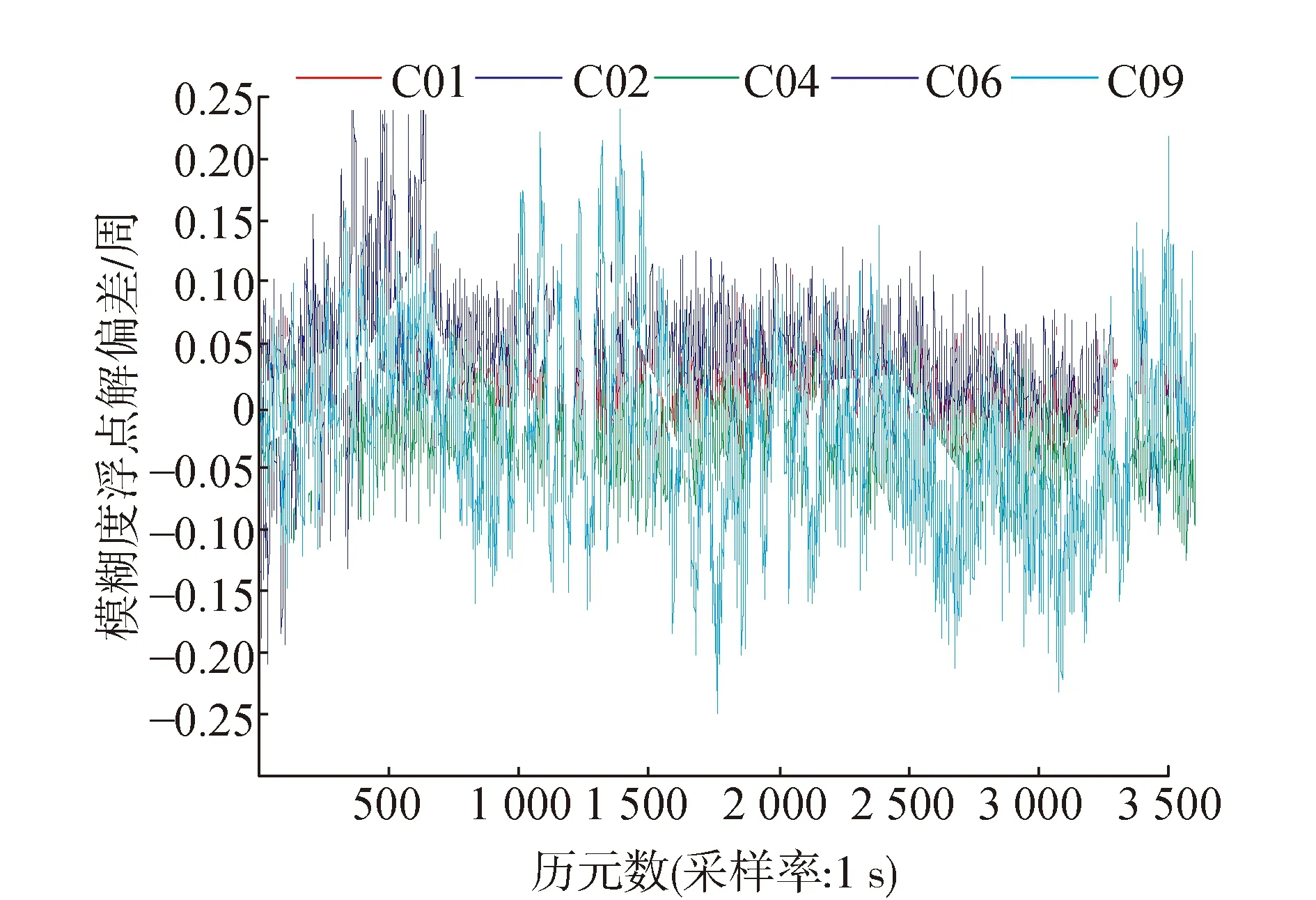
图4 基线 LHNF-MAQN N(0,-1,1)组合模糊度偏差

图5 基线LHNF-MAQN N(1,4,-5)组合模糊度偏差
从图2和图4看出,两组基线(0,1,-1)组合模糊度偏差均很小,均在±0.2周之内,因此按照单历元四舍五入直接取整可获取到模糊度的固定解。从图3和图5看出,两组基线(1,4,-5)组合的模糊度偏差均大于(0,1,-1)组合模糊度偏差,但其偏差仍然在±0.4周,在解算区间内按照四舍五入原则也能直接取整得到模糊度的固定解。
3.2 BDS约束固定GPS宽巷模糊度
为验证BDS约束固定GPS宽巷模糊度的准确性,分别计算两组基线采用LAMBDA算法固定GPS宽巷模糊度时的Ratio值并进行统计,其结果如图6—图7和表3所示。

图6 基线JNNF-LHNF GPS宽巷模糊度固定Ratio值

图7 基线LHNF-MAQN GPS宽巷模糊度固定Ratio值

表3 BDS约束GPS宽巷模糊度固定Ratio值统计结果 %
从图6—图7和表3可以看出,对两个中长基线而言,采用BDS宽巷模糊度辅助固定GPS宽巷模糊度,其Ratio值均大于2,且Ratio值大于5的均超过97%,因此,采用这种方式实现GPS宽巷模糊度的单历元固定是可行的。
4 结束语
针对目前绝大部分GPS卫星仅能播发双频观测信息而无法实现宽巷模糊度单历元固定的问题,本文利用北斗三频超宽巷组合长波长特性,利用超宽巷组合实现BDS宽巷模糊度单历元固定,然后利用BDS约束GPS,实现了BDS/GPS双系统宽巷模糊度的单历元固定。采用南京计量院CORS两条基线解算发现基于本文数据的单历元宽巷模糊度固定方法,BDS超宽巷均可实现单历元取整固定,GPS宽巷模糊度固定Ratio值均大于2,因此采用本文方案实现BDS/GPS宽巷模糊度分层逐级单历元固定是可行的。
[1] 杨元喜. 北斗卫星导航系统的进展、贡献与挑战[J]. 测绘学报, 2010, 39(1):1-6.
[2] 杨元喜, 李金龙, 王爱兵,等. 北斗区域卫星导航系统基本导航定位性能初步评估[J]. 中国科学(地球科学), 2014(1):72-81.
[3] FENG Y. GNSS three carrier ambiguity resolution using ionosphere-reduced virtual signals[J]. Journal of Geodesy, 2008, 82(12):847-862.
[4] TANG W, DENG C, SHI C, et al. Triple-frequency carrier ambiguity resolution for Beidou navigation satellite system[J]. Gps Solutions, 2014, 18(3):335-344.
[5] TEUNISSEN P J G. Influence of ambiguity precision on the success rate of GNSS integer ambiguity bootstrapping[J]. Journal of Geodesy, 2007, 81(5):351-358.
[6] ZHAO Q, DAI Z, HU Z, et al. Three-carrier ambiguity resolution using the modified TCAR method[J]. Gps Solutions, 2015, 19(4):589-599.
[7] 范建军, 王飞雪. 一种短基线GNSS的三频模糊度解算(TCAR)方法[J]. 测绘学报, 2007, 36(1):43-49.
[8] 李博峰, 沈云中, 周泽波. 中长基线三频GNSS模糊度的快速算法[J]. 测绘学报, 2009, 38(4):18-23.
[9] LI B, FENG Y, SHEN Y. Three carrier ambiguity resolution: distance-independent performance demonstrated using semi-generated triple frequency GPS signals[J]. Gps Solutions, 2010, 14(2):177-184.
[10] 李金龙, 杨元喜, 何海波,等. 函数极值法求解三频GNSS最优载波相位组合观测量[J]. 测绘学报, 2012, 41(6):797-803.
[11] LI J, YANG Y, XU J, et al. GNSS multi-carrier fast partial ambiguity resolution strategy tested with real BDS/GPS dual- and triple-frequency observations[J]. Gps Solutions, 2015, 19(1):5-13.
[12] 何俊, 刘万科, 张小红. 北斗短基线三频实测数据单历元模糊度固定[J]. 武汉大学学报(信息科学版), 2015, 40(3):361-365.
[13] 刘炎炎, 叶世榕, 江鹏,等. 基于北斗三频的短基线单历元模糊度固定[J]. 武汉大学学报(信息科学版), 2015, 40(2):209-213.
[14] 吴波, 高成发, 高旺,等. 北斗系统三频基准站间宽巷模糊度解算方法[J]. 导航定位学报, 2015(1):36-40.
[15] 高旺, 高成发, 潘树国,等. 北斗三频宽巷组合网络RTK单历元定位方法[J]. 测绘学报, 2015, 44(6):641-648.
[16] GAO W, PAN C G S. Single-Epoch Navigation Performance with Real BDS Triple-Frequency Pseudorange and EWL/WL Observations[J]. Journal of Navigation, 2016, 69(6):1293-1309.
[17] WANG G, CHENGFA G, SHUGUO P, et al. Improving Ambiguity Resolution for Medium Baselines Using Combined GPS and BDS Dual/Triple-Frequency Observations[J]. Sensors, 2015, 15(11):27525-42.
[18] WANG S, DENG J, LU X, et al. A New GNSS Single-Epoch Ambiguity Resolution Method Based on Triple-Frequency Signals[J]. ISPRS International Journal of Geo-Information, 2017, 6:46.

