动车组车轮踏面磨耗的镟修优化策略研究*
耿绮灵, 石玉红, 尹继东, 高薇薇
(西南交通大学 数学学院,成都 611756)
0 引 言
当列车在高速行驶的过程中,特别是在轮对通过弯道时,轮对轮缘部分受到的较大摩擦力使得轮缘发生了磨耗,而当磨耗过度时,容易导致车轮折断,造成脱轨事故,严重威胁着行车安全[1]。为了使得高速动车组轮对能够继续正常使用,必须对磨损的轮对进行镟修,以恢复其技术标准规定的几何形状,再次投入使用。由于往往是通过减少轮径来恢复轮缘厚度,因此,轮径会不断减少,直到最终达到报废的限度[2]。由于我国目前高速动车组轮对购置成本较高,因此对高速动车组轮对进行有效的优化镟修既能够保障高速动车行车安全,又能提高车轮的使用寿命,并降低成本费用。因此,对高速动车组轮进行有效的优化镟修具有非常重要的现实意义[3]。
有关统计资料表明:车轮踏面直径每损失1 mm,车辆可运行的里程将减少10万km;而当车轮磨耗显著影响车辆动力学性能,需要进行镟修时,按照传统的车轮镟修方法,磨耗后的车轮轮缘厚度每次镟修恢复1 mm,踏面直径将损失约4.2 mm[4],而当车轮异常偏磨时,踏面直径需要镟去10 mm之多,因此,车轮优化镟修的方案直接关系动车组运输的维护成本。
1 轮对镟修概述
主要对踏面和轮缘产生了磨耗的动车车轮,进行镟修策略的优化设计。由于车轮产生的磨耗主要是在轮缘部分,因此,恢复镟修后的踏面镟修量,除了一部分是由于正常磨损导致的,另一部分则是由于镟修导致的。按照技术标准的规定,轮径H的范围在790 mm≤H≤860 mm之间,轮缘厚度B在26 mm≤B≤32 mm之间。
因此,每恢复1 mm的轮缘厚度,相应的轮径减少量是衡量镟修方案优劣的标准。通过式(1)可衡量每恢复1 mm的轮缘厚度所损失的轮径量大小,称之为镟修比例系数。具体的镟修前后轮径减少量和轮缘厚度减少量变化情况见图1所示,其中轮缘厚度是指轮缘顶向下27 mm的厚度。
(1)
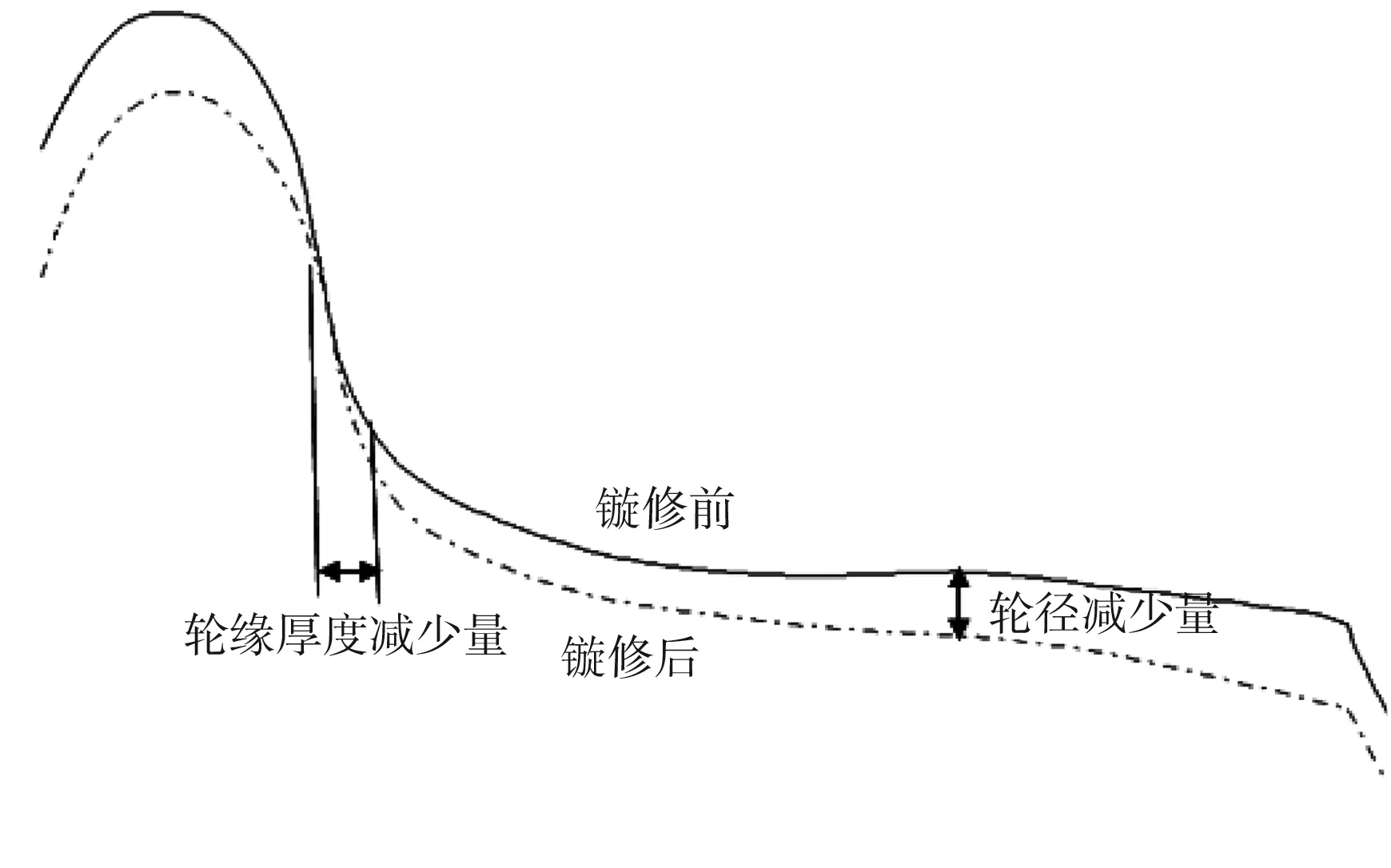
图1镟修比例系数图
Fig.1Theproportionalitycoefficientdiagramofrotation
在进行车轮镟修时,若轮缘厚度恢复量少,则轮径损失相对应就少,但相对于下次轮缘厚度达到极限值的吋间就会提前,这会增加镟修费用和镟修次数;若轮缘厚度恢复量多,则轮径损失相对应就多,使得轮径尺寸提前达到极限值而报废。因此,当对轮对进行镟修时,需要充分考虑如何才能使得每恢复1 mm的轮缘厚度量所对应的轮径损失相对而言更少,从而优化镟修量。因此,需要通过模型对车轮镟修优化进行分析和研究[5]。
2 单个车轮镟修优化模型
传统的镟修方案将磨耗后的车轮恢复成LM-26型,LM-28型,LM-30型和LM-32型4种标准的外形轮廓。为了构建镟修优化模型,前期工作分析了动车车轮轮缘厚度以及圆弧连接的变化规律,设计出轮缘厚度能够连续变化的轮缘踏面外形几何构型,如图2所示。
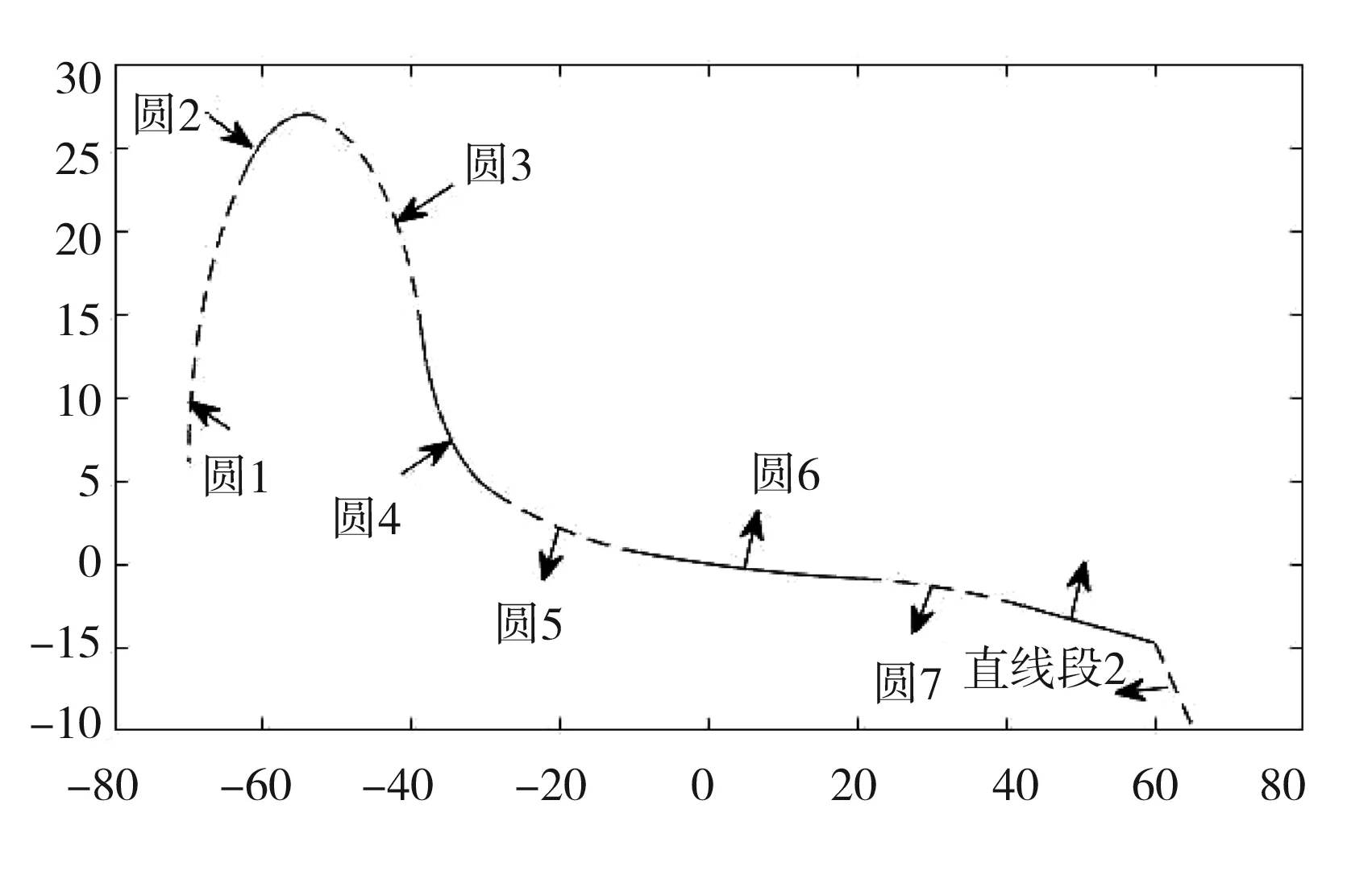
图2 轮缘踏面外形示意图
通过构建车轮几何型面方程,可以达到使车轮的轮缘厚度连续变化的目的,并且由图2可以观察到构成车轮的各圆弧之间都是光滑连接的,能够有效描述动车车轮几何形状。在基础工作完成之后,构建车轮镟修优化模型流程如下。
2.1 原始数据处理
(1) 处理异常数据。原数据中x坐标的值从小到大排列,分别对应唯一的y坐标的值,且y坐标的值的分布也有一定的规律性,使得通过原数据可以画出轮缘踏面曲线。因此,对于“一个x值对应不同y值”以及“x值出现反复现象”的数据进行剔除处理。
(2) 原数据标准化。由于原数据给出的坐标信息并不同于已建立的坐标系,因此,需要将原数据标准化到已建立的坐标系上来。按照磨耗规律,对于踏面曲线的尾部,磨损非常少,可以找到磨损几乎为零的部分。实际上,倒角部分基本不磨损,因此,可以获取原始数据中倒角部分转折点,将其与标准曲线模型中的点xΔ=L-70-5比较,计算出实际数据中曲线的位移量,对原始数据进行平移处理,得到已建立坐标系下的标准数据。
倒角部分转折点确定方法如下:通过求各点(xi,yi)处的斜率ki
(2)
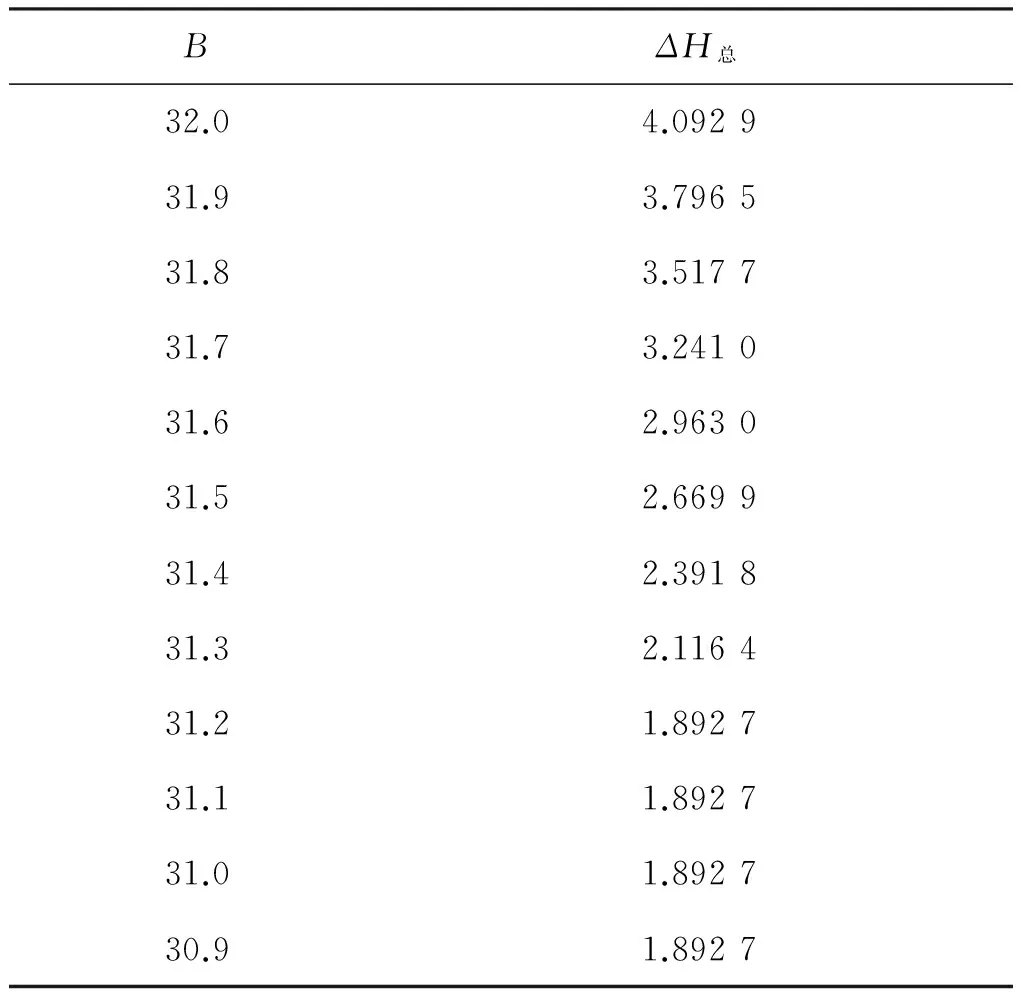
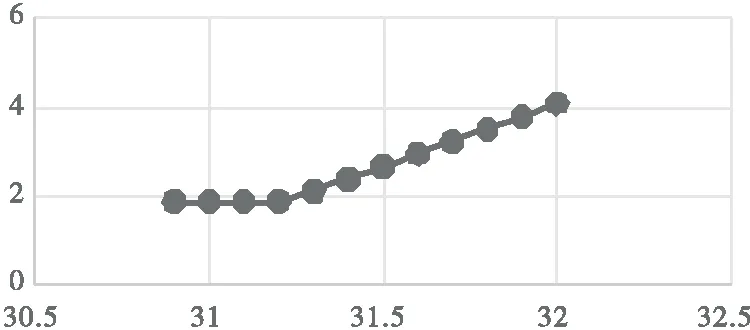
从尾部斜率数据开始寻找转折点,当-0.2 轮缘厚度变化范围为B∈[26.2,32.0];由于标准轮径坐标为27 mm,最大轮径镟修量为70 mm,因此轮径变化范围为H∈[-43,27](单位:mm)。 从标准化后的数据搜索出纵坐标在11.7 (1) 从B=32 mm,H=27 mm的标准轮缘外形轮廓曲线方程开始,连续改变轮缘厚度B,得到新的轮缘厚度Bnew=B-n1×ΔB,其中,ΔB为每次轮缘减少量,n1为轮缘厚度减少的次数。 (2) 对于每一个新的轮缘厚度Bnew,通过搜索的方式,从H=ym处,连续减少H,使得Hnew=H-n2×ΔH,其中,ΔH为每次轮径减少量,n2为轮径减少的次数。直到新得到的曲线方程L(Bnew,Hnew,x,y)=0与经过标准化后的数据的曲线方程L标(x,y)=0至多只有一个交点为止,即 (3) 联立得到的交点坐标,(x交1,y交1),…,(x交k,y交k),其中k≤1。 (3) 根据不同曲线方程L(Bnew,Hnew)的参数Bnew和Hnew,选取目标优化条件 (4) 即将恢复一单位轮缘厚度所需轮径减少量最少的情况,作为最优的情况。 具体的优化模型如下所示 (5) (6) (1) 初始化参数。每次轮缘减少量ΔB设为0.1 mm,每次轮径减少量ΔH设为0.000 1 mm。对动车车轮采用检测装置进行长期轮缘踏面数据测量和记录,选取其某一车厢的第二个左侧车轮的轮缘踏面数据进行分析讨论,经过测量,其轮缘厚度为B=30.45 mm。 (2) 各轮缘厚度B以及搜索到的轮径减少量(ΔH总)如表1所示。 表1 各轮缘厚度以及搜索到的轮径减少量 数据来源:检测装置对车轮踏面现场采集数据“301701-10-05”部分数据。 由表1中的数据可以作出散点直线图,如图3所示。 图3 各轮缘厚度以及搜索到的轮径减少量散点图 由图3可以观察到,当轮缘厚度从32.0 mm减少到31.2 mm时,与所损失的轮径量基本呈现直线减少的关系。当轮缘厚度低于31.2 mm时,所损失的轮径量基本不变。 相应的,随着轮缘厚度减少,镟修结果如图4-图6所示。 在图4中,实线部分为镟修前轮缘踏面图,点画线部分为轮缘厚度为32 mm时的镟修结果。 在图5中,实线部分为镟修前轮缘踏面图,重叠的点画线部分为轮缘厚度为31.2 mm至32 mm时的镟修结果。可见,当恢复的轮缘厚度越小时,所需镟掉的轮径也越少。 图4 一次镟修示意图 图5 多次镟修示意图 图6 轮缘厚度为31.2 mm和30.2 mm时的镟修结果示意图 图6中,实线部分为镟修前轮缘踏面图,点画线和虚线部分分别为轮缘厚度为31.2 mm和30.2 mm时的镟修结果。可见,当轮缘厚度小于31.2 mm时,通过减少轮缘厚度已经不能使所需镟掉的轮径减少,因此,当轮缘厚度小于31.2 mm时,继续减少轮径将会产生过度镟修的问题。 根据表2中的数据作图如下,详见图7。 由图7可知,当轮缘厚度在30.0 mm至31.0 mm之间时,z比缓慢下降;在31.0 mm至31.3 mm之 间时,z比急速下降,并到达最小点处;而轮缘厚度为31.3 mm至32.0 mm时,z比较轮缘厚度为30.0 mm至31.0 mm时的小。 表2 各轮缘厚度对应的z值 图7各轮缘厚度对应的z值散点图 Fig.7Scatterdiagramofzscores 由于模型试算数据选取了动车第二个左车轮的轮缘踏面数据,车轮轮缘厚度为B=30.45 mm。 如果采用传统镟修方式,那么需要将车轮镟修为标准的LM-32型或者LM-30型,其轮缘厚度分别为32.0 mm以及30.2 mm。 若采用轮缘厚度为32.0 mm的镟修方案,那么,轮径需要镟掉4.092 9 mm,z比为2.633 6。若采用轮缘厚度为30.2 mm的镟修方案,那么轮径需要镟掉1.892 7 mm,并且没有恢复轮缘厚度,这将会使得轮缘厚度减少速度加快,提前到达需要返修的极限值,并大大减少车轮可镟修次数,提高车轮维护成本,不利于镟修的经济化。 比较轮缘厚度为32.0 mm和轮缘厚度为31.3 mm的镟修情况,轮缘踏面轮廓各点镟修量如图8所示。 图8 轮缘厚度分别为32.0 mm和31.3 mm的镟修量 由图8所示,实线部分表示轮缘厚度为32.0 mm的镟修情况,虚线部分表示轮缘厚度为31.3 mm的镟修情况。可见,在最大磨损点处对车轮基本不进行镟修。而镟修成轮缘厚度为32.0 mm的镟修方案中,除最大磨损点外的其余各点处的镟修量明显大于轮缘厚度为31.3 mm的镟修方案。 比较轮缘厚度为31.3 mm和轮缘厚度为30.2 mm的镟修情况,轮缘踏面轮廓各点镟修量如图9所示。 如图9所示,虽然在除了最大磨耗点附近的部分点以外,轮缘厚度为30.2 mm的镟修方案相对于轮缘厚度为31.3 mm的镟修方案镟修的少,但是,在最大磨耗点附近出现了过度镟修的现象,这将大大增加镟修的成本,不利于车轮镟修的经济化。 图9 轮缘厚度分别为31.3 mm和30.2 mm的镟修量 传统的镟修方案将磨耗的车轮恢复成LM-26型,LM-28型,LM-30型和LM-32型这一系列固定轮缘厚度的车轮形状,极易产生过度镟修问题,通过对动车车轮型面进行几何化建模,在轮缘踏面外形的轮缘厚度能够连续变化的基础上,对轮缘厚度的减少量和轮径的减少量建立优化模型,给出优化方案,经过可行性分析发现,优化方案具有避免轮缘处产生过度镟修,以及使轮缘厚度尽可能大,以提高车轮生命周期等优点,具有实际应用价值。 [1] 黄照伟. 车轮磨耗及其对车辆动力学性能的影响[D]. 成都:西南交通大学, 2012 HUANG Z W. Wheel Abrasion and Its Effect on Vehicle Dynamics[D].Chengdu:Southwest Jiaotong University,2012 [2] 徐伟民. 车轮轮辋和轮缘厚度关系的探讨[J]. 铁道车辆, 2004,42(7):41-42 XU W M. The Relationship between Wheel Rim and Rim Thickness[J]. Railway Vehicle, 2004,42(7):41-42 [3] 藤沢孝之. 车轮踏面管理与经济镟修[J]. 国外机车车辆工艺, 1995(4):13-17 TENG C X Z. Wheel Rread Management and Planning, Economic Rotation[J]. Foreign Locomotive Vehicle Technology, 1995(4):13-17 [4] 员华,肖胜强,汪洋. 基于磨耗量统计的轮对等级镟修可行性分析[J].城市轨道交通研究, 2006(1):43-45 YUAN H, XIAO S Q, WANG Y. The Feasibility Analysis of the Rotation Based on the Measurement of Grinding Consumption[J]. Urban Rail Transit Research, 2006(1):43-45 [5] 贾小平. 机车轮缘磨耗问题的研究[D]. 大连:大连交通大学, 2010 JIA X P. Study on the Friction of Locomotive Wheel Rim[D]. Dalian:Dalian Jiaotong University, 2010 [6] 刁晓明. 服役动车组车轮磨耗及振动性能跟踪研究[D]. 北京:北京交通大学, 2014 DIAO X M. The Track Research on Wheel Wear and Vibriation Performance of the Service EMU in China[D].Beijing:Beijing Jiaotong University, 2014 [7] 王珍. 动车组整车轮对镟修优化决策模型的研究[D]. 成都:西南交通大学,2013 WANG Z. Study on the Model of the Re-profiling Strategy Optimization about the Whole Wheelset Wearing Electric Multiple Unit[D]. Chengdu:Southwest Jiaotong University, 2013 [8] 任文娟. 高速动车组车轮型面优化研究[D] . 成都:西南交通大学,2015 RENG W J. Research on High-Speed EMU Wheel Profile Optimization[D].Chungdu:Southwest Jiaotong University, 2015 [9] 董孝卿. 高速动车组车轮踏面镟修策略研究[J]. 中国铁道科学,2013(4):101-108 DONG X Q. Research on the Reprofiling Strategy for the Wheel Tread of High-Speed EMU[J]. China Railway Science, 2013(4):101-1082.2 参数范围设定及模型优化
2.3 单个车轮镟修优化模型

3 单个车轮镟修优化模型试算
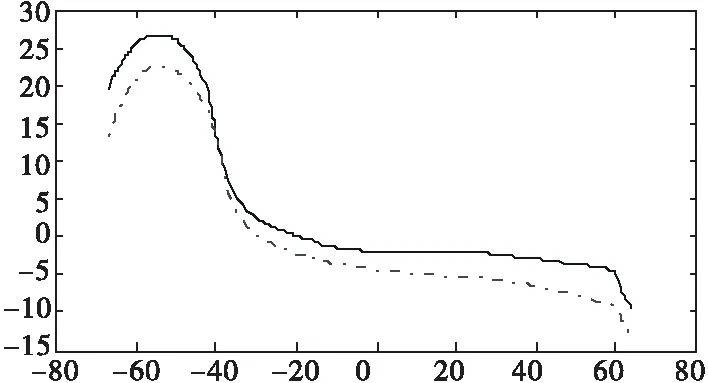
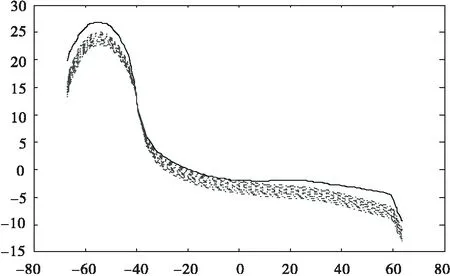
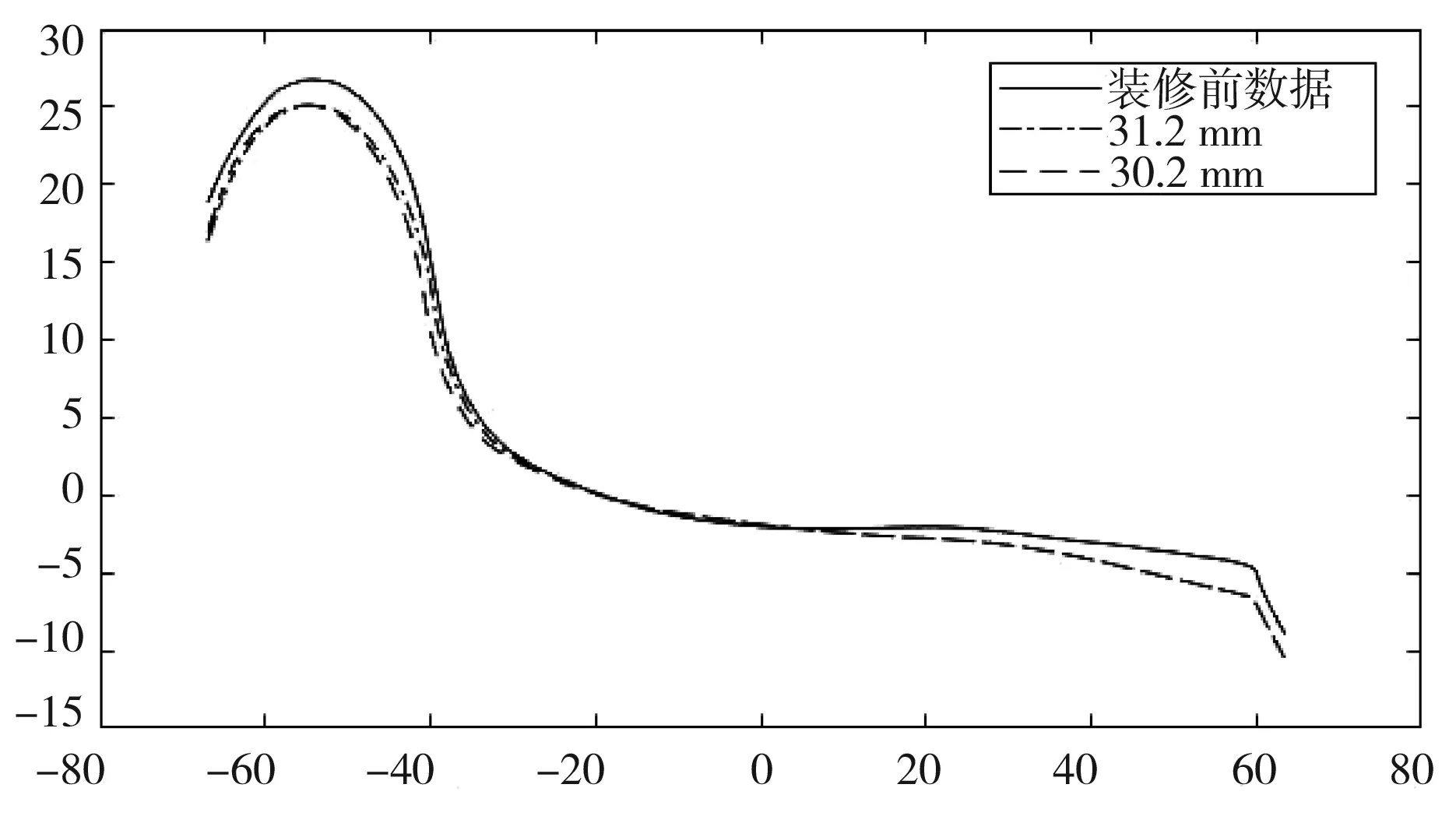
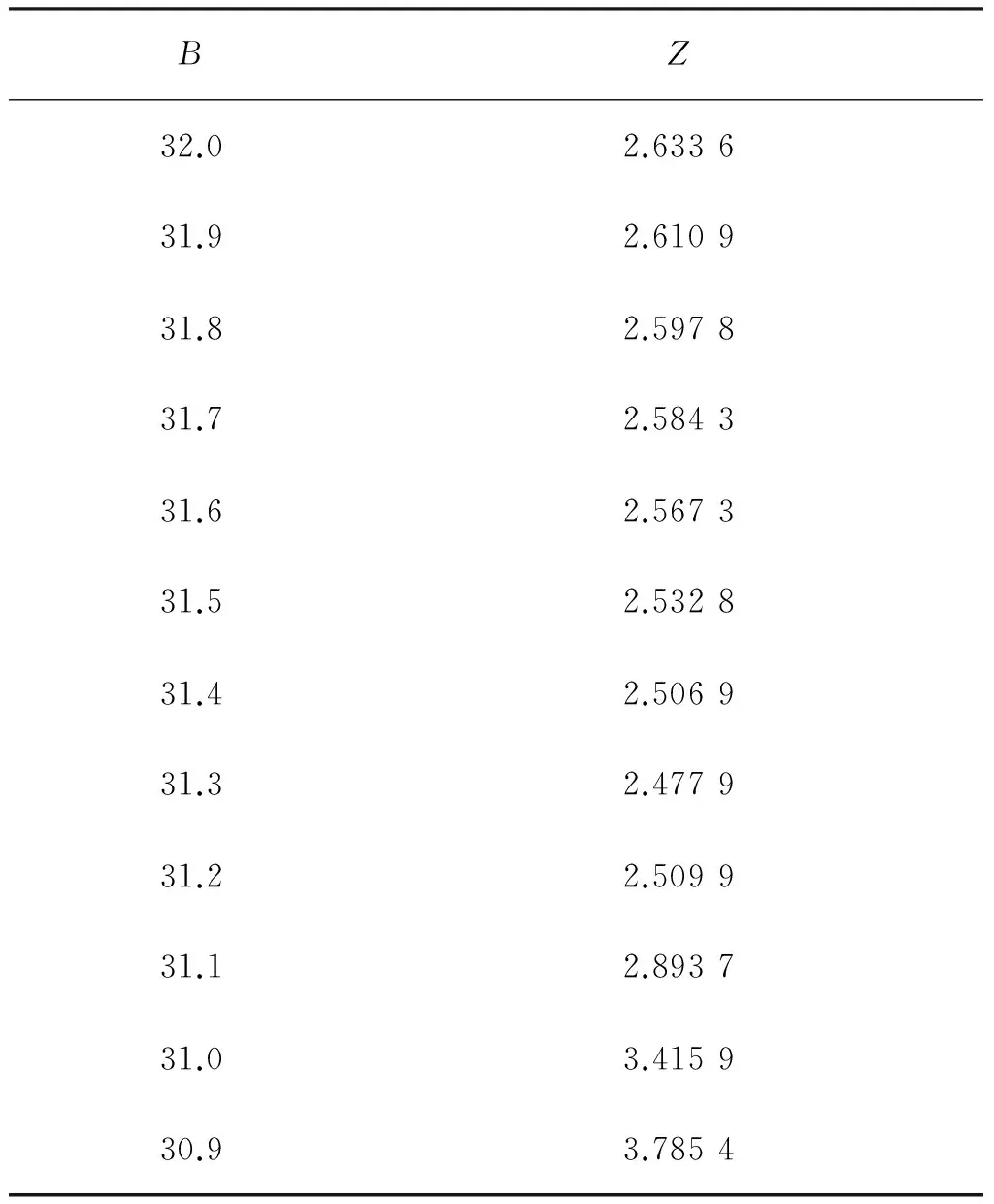
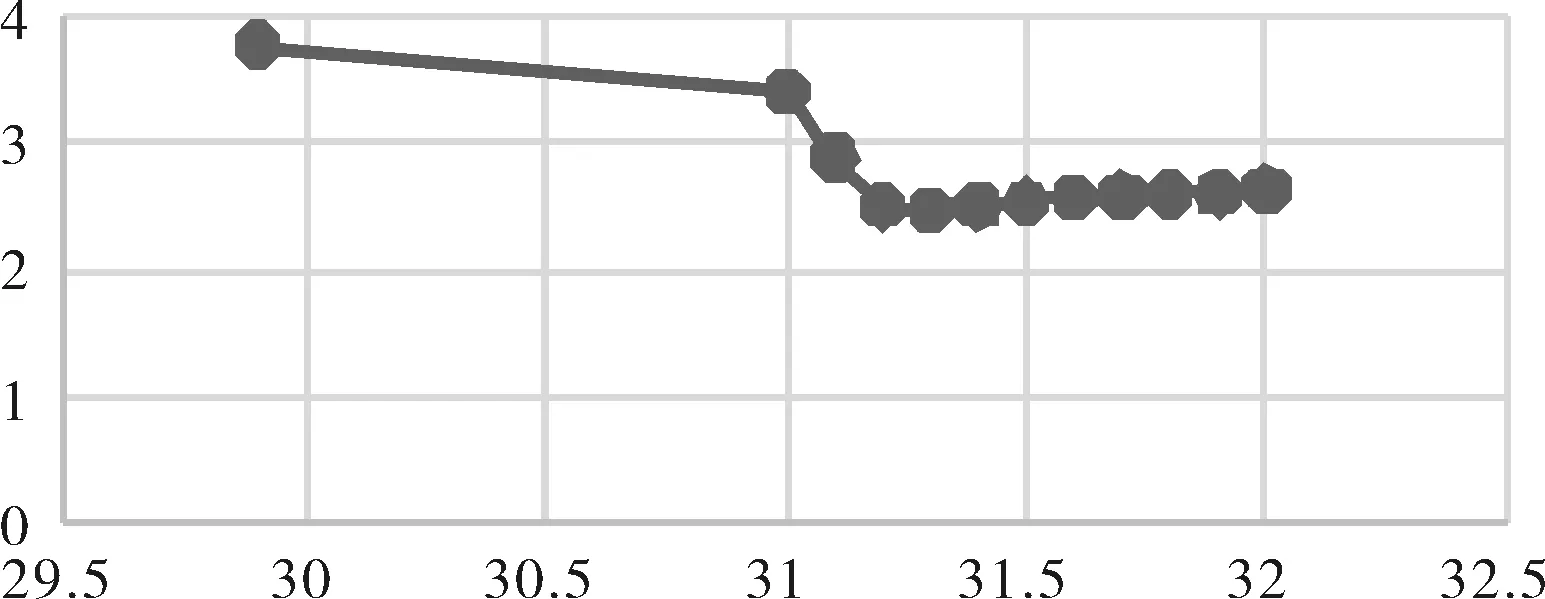
4 模型结果可行性与有效性分析
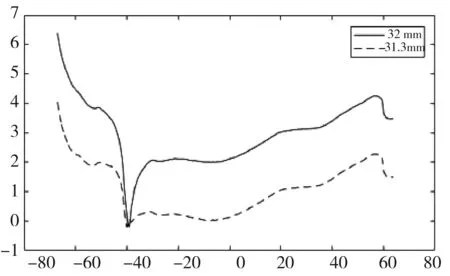
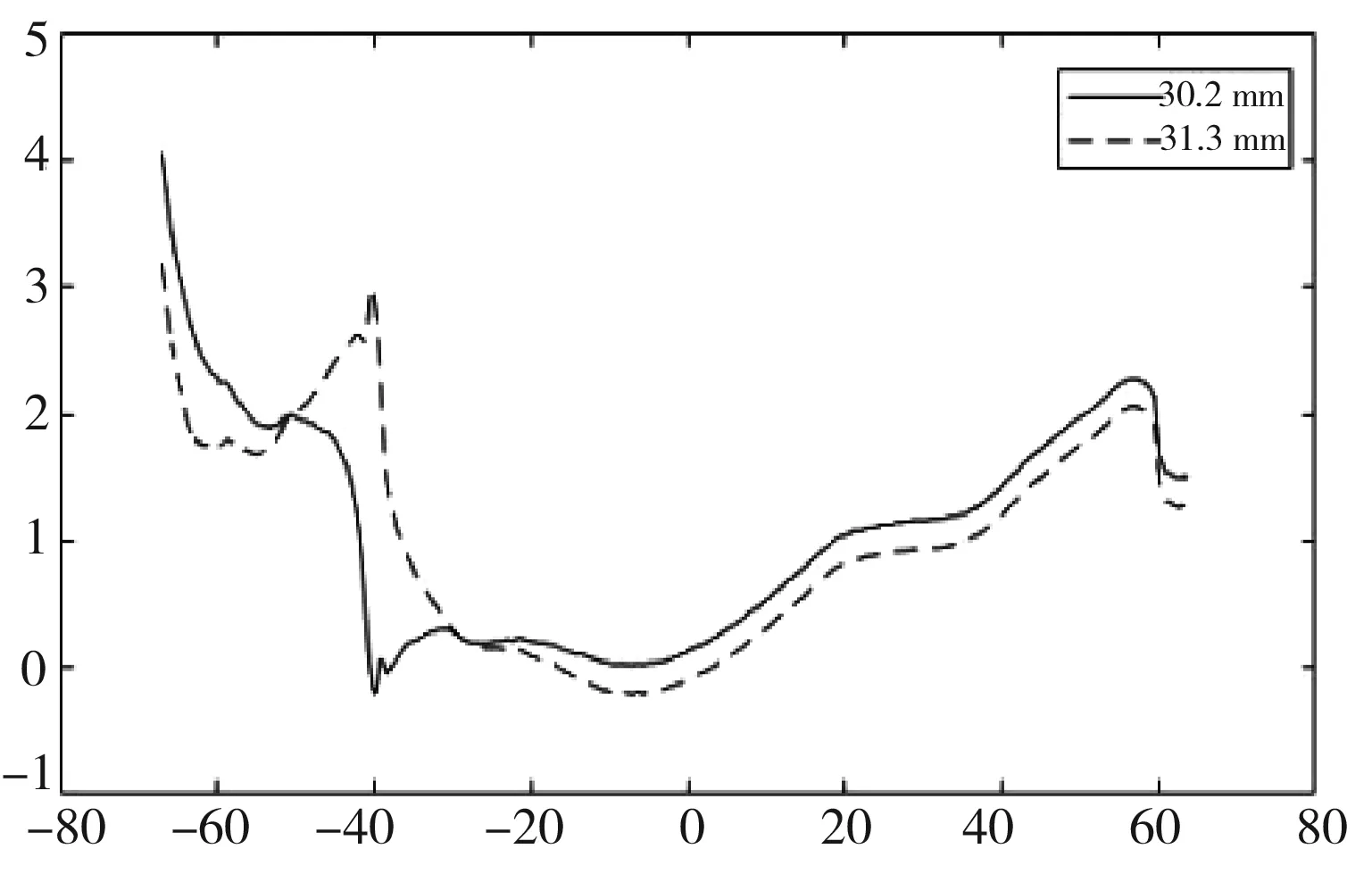
5 结 论

