强噪声干扰下MR图像的脑组织分割

赵海峰，夏国峰，宋维明，张少杰

安徽大学计算机科学与技术学院，合肥230601

强噪声干扰下MR图像的脑组织分割

赵海峰，夏国峰，宋维明，张少杰

安徽大学计算机科学与技术学院，合肥230601

CNKI网络出版：2017-04-14,http://kns.cnki.net/kcms/detail/11.2127.TP.20170414.1717.002.html

1 引言

医学图像分割常常是计算机辅助诊断[1]过程的初步阶段，也是必不可少的阶段，特别是用在核磁共振图像的临床分析上。医学图像包括核磁共振图像（MRI）、电子计算机断层扫描（CT）以及PET图像等等。由于不同的成像原理，图像所体现的特点有所差异。MR（Magnetic Resonance）图像相对于其他图像有自身的特点，比如，对于不同的软组织有强烈的对比度，以及自身具有较高的空间分辨率[2]。脑组织分割大部分是针对白质（WM）、灰质（GM）以及脑脊液（CSF）的分割，因此非常适合使用MR图像进行分割。医学图像通常易受到干扰，比如噪声干扰、灰度不均匀、局部体积效应等等，并且在图像边缘部分对比度较弱[3]，针对不同条件下的MR图像能够得到较好的分割结果，便成了学者们研究的热点。

传统的分割方法包括基于阈值的方法、基于聚类的方法、基于区域的方法、基于边缘的方法以及基于图论的方法等[4]。针对各种干扰因素，学者们都提出了各自的想法。其中模糊聚类的方法应用非常广泛，文献[5]首次提出了模糊C均值（FCM）算法，将模糊度的概念引入到聚类方法中。文献[6]提出了优化的偏置场估计和组织分割方法，通过偏置场估计和组织分割同时迭代进行，使最后分割精度有所提高，并且算法对初始化非常鲁棒。文献[7]提出了基于空间关系的模糊C均值算法，该算法利用窗口内的所有点的隶属度之和这一空间信息，整合到传统模糊C均值当中，对噪声有一定的鲁棒性。

噪声干扰一直是医学图像重要干扰因素之一，由于人体脑部组织结构的复杂性以及核磁共振技术的成像机理等方面原因，MR图像会呈现强噪声，伪影像以及弱边界等现象，比如传统的活动轮廓模型，由于往往仅使用目标边缘信息，导致在处理强噪声图像时会过早停止，并且在边界模糊时会出现弱边界泄露现象。另外很多研究采用灰度信息和空间信息来抑制噪声干扰，文献[8]在FCM的目标函数中引入局部空间项，使算法性能更好。文献[9]将传统的欧式距离替换成核距离，使算法的鲁棒性更好。文献[10]整合了空间信息和灰度信息，提出了基于模糊因子的FLICM算法，算法FLICM的鲁棒性不错，但是每次迭代都要计算模糊因子，时间复杂度大，并且模糊因子受欧氏距离影响严重，容易使图片失去细节信息。文献[11]提出了新的模糊因子，并且引入了核距离，该方法对噪声显得更加鲁棒。文献[12]提出了基于核的自适应正则化的模糊C均值算法，该方法引入自适应参数，并且使用均值滤波、中值滤波以及自定义滤波图像，不用每次迭代计算参数，大大节约了时间成本，同时提高了算法对噪声的鲁棒性。文献[13]通过对图像进行分块压缩提高了重建图像的质量以及压缩率。

综上所述，本文提出一种基于核的正则化局部空间聚类算法，本文采用自适应参数给图像中所有点预先分配参数值，节约计算成本；并且引入核距离度量方法，同时加入隶属度惩罚项，使聚类效果更加明显；最后加入空间信息约束，使得算法对噪声点更加鲁棒。

本文第2章主要介绍模糊C均值以及核距离；第3章重点介绍KASFCM方法，在第4章的仿真实验中，利用Brainweb提供的数据，分别与其他几种方法对比，最后得出本文结论。

2 模糊C均值聚类和核距离

2.1 模糊C均值聚类

模糊C均值聚类[5]，是用隶属度确定每个数据点属于某个聚类的程度的一种聚类算法，该算法采用迭代优化目标函数的方法对数据进行分类，在数学上可以表达为对目标函数求极值的问题，即

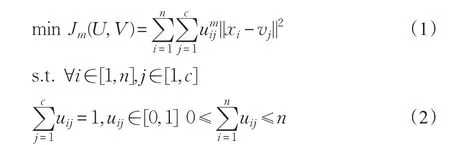
其中，m是控制模糊度的模糊权重因子，xi是像素点，vj是聚类中心，uij表示第i个像素点属于第j个类的隶属度，通过对目标函数求极值可以得到：

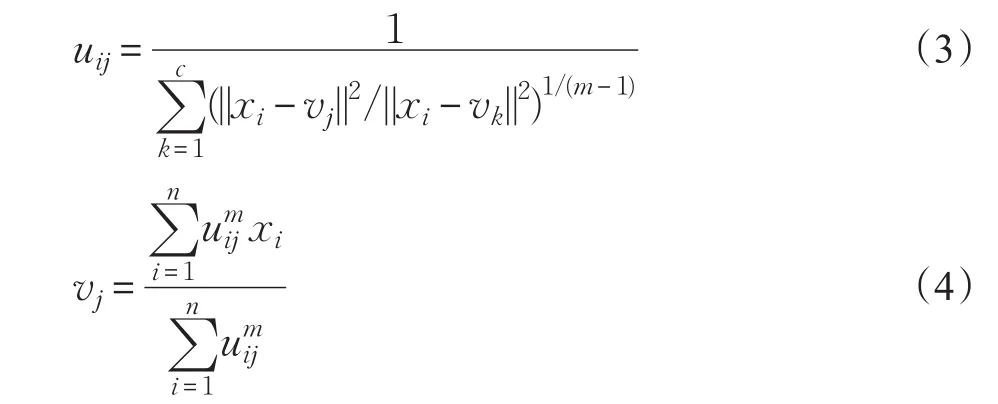
通过对式（3）、（4）反复迭代可以得到最终的隶属度矩阵和聚类中心。

2.2 核距离

传统的欧式距离优点是简单而且计算量不大，但是它的局限性大，对圆形或者椭圆形的区域比较有效，而对其他区域效果不是很好。文献[14]采用颜色共生矩阵提取图像纹理特征，并且计算图像相似性，该方法主要应用于彩色图像处理。近年来，由于支持向量机的广泛使用，核函数也受到了重视。核函数将低维空间映射到高维空间[15]，该映射的目的是把非线性关系转化为线性关系。将欧式距离替换成核距离并且核距离定义为：

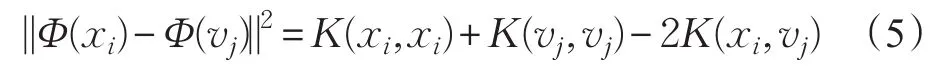
其中K是核函数。在这里，采用高斯核函数[16]：

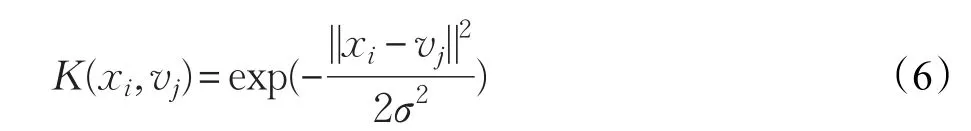
其中σ为高斯核参数。使用高斯核函数过后，式（5）即化为：

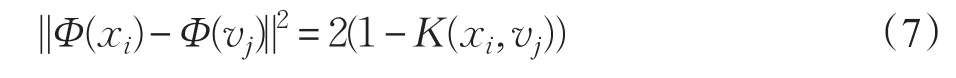
3 基于核的正则化局部空间聚类算法（KASFCM）

为了使本文的算法对更强的噪声鲁棒，使用自适应正则化参数，并将参数应用到本文的目标函数上。

首先，定义一个局部方差系数L，并且计算窗口内所有点灰度值的均值：

接下来将它们投影到核空间，然后将投影后的权重进行标准化[12]：模糊划分更加分明。利用拉格朗日乘数法分别对目标函数关于uij、vj求偏导，可得到算法的隶属度函数uij和聚类中心vj的更新公式为：

最终，通过每个像素点与均值像素比较来为每个点分配权重，如下：

参数λ是对图像每个像素点计算得到的自适应参数，它充分利用点的上下文信息，在迭代过程开始之前，为每个像素点分配好权重，因此减少了算法的时间复杂度。

将参数ρ同时引入到目标函数的两项表达式中，得到：

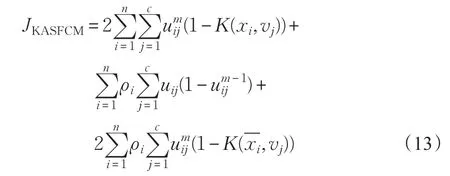
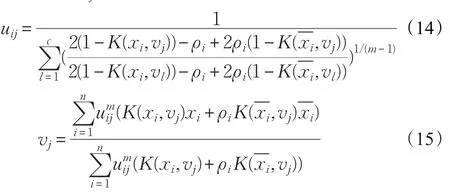
为了使算法对强噪声更加鲁棒，在算法中加入局部空间关系。因为图像中点与点之间的关联性很高，也就是说相邻的点之间拥有相似的特征，因此它们属于同一个类的可能性就很大，引用文献[7]提供的空间信息，空间函数定义如下：

其中NB(xi)表示的是以xi为中心点的窗口，本文采用的是5×5的窗口，这里的sij类似于隶属度uij，表示的是像素点属于某个类的可能性，如果sij越大，表示中心点的窗口内大多数点属于某个类，最后把空间函数整合到隶属度函数中：

这里的参数p，q是用来控制空间函数和隶属度函数的权重，本文的实验取p=2，q=1。下面是算法的具体执行步骤：

（1）初始化参数：p=2，q=1，m=2，迭代次数t=0，阈值ε=0.001，u(0)和v。

（2）计算自适应正则化参数ρi。

（5）利用式（14）计算隶属度函数u(t+1)。

（7）利用式（16）、（17）加入并整合空间关系，得到最终的隶属度函数uij'。

4 实验仿真

实验中采用模拟大脑数据库（SBD，http：//brainweb.bic.mni.mcgill.ca/brainweb/）提供的数据进行分析。选择噪声强度为9%的图像作为实验数据，在3%、5%、7%的噪声下，实验效果与其他同类算法均保持较好的分割效果，但是当加入10%的莱斯（Rician）噪声，实验结果充分说明算法具有更好的鲁棒性。在这里，将本文的方法分别与ARKFCM[12]、MICO[6]、KWFLICM[11]以及SFCM[7]等算法进行定性定量分析。

首先，对图像进行头骨剥离等预处理，图1是采用9%的噪声图像，分别应用不同算法得到的分割结果，其中ARKFCM1和KASFCM1表示使用均值滤波图像进行分割的结果，ARKFCM2和KASFCM2表示使用中值滤波图像进行分割的结果。图2是针对图1的分割结果局部放大的效果展示，能够清晰地看出各个算法分割的细节信息。从图中可以看出，MICO和SFCM对强噪声非常敏感，并且在细节保留方面能力较弱，虽然KWFLICM对噪声不是特别敏感，但是在细节保留上差很多，大多表现在上下部分的灰质和脑脊液之间，没有把它们区分开；ARKFCM对强噪声分割在聚类效果和细节上，分割后的图像中仍出现很多噪声点，并且图像边缘效果处理比较粗糙；而本文的算法可以很好地分割出目标区域，并且体现出对强噪声很好的鲁棒性，在图像边缘部分，本文的算法效果更加平滑。

为了更加充分的证明算法的抗噪性，采用峰值信噪比（PSNR）来衡量，峰值信噪比越大代表去噪效果越明显，反之则越差。从图3可以看出，本文算法峰值信噪比提升较高，MICO算法由于分割后仍然存在大量噪声点，把噪声和非噪声混淆，所以PSNR较低，而其他同类算法由于对噪声点的去除效果较差，峰值信噪比都低于本文得到的值。有时，图像中的噪声虽然得到抑制，峰值信噪比得到提高，但是图像的边缘和细节信息会有不同程度的损失，比如KWFLICM算法。

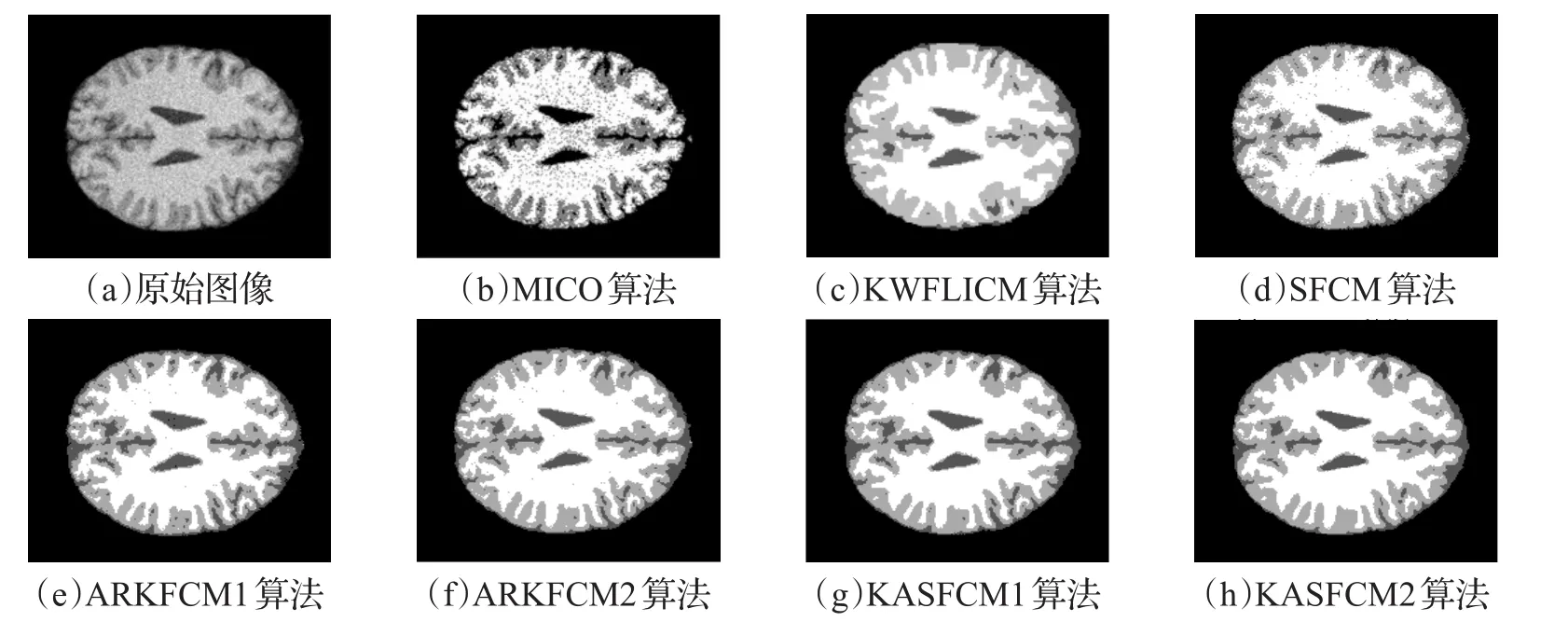
图1 9%噪声图像不同算法分割结果

图2 9%噪声图像不同算法分割结果局部放大图

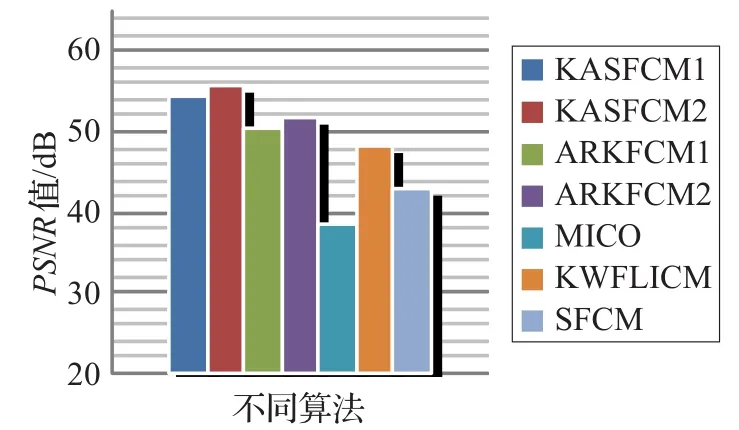
图3 9%噪声图像不同算法分割结果峰值信噪比对比

为了定量地分析算法的聚类效果，使用两种类型的聚类验证函数来进行评价：基于模糊分割的评价函数和基于特征结构的评价函数。基于模糊分割的评价函数有分割系数Vpc[17]和分割熵Vpe[18]，定义如下：

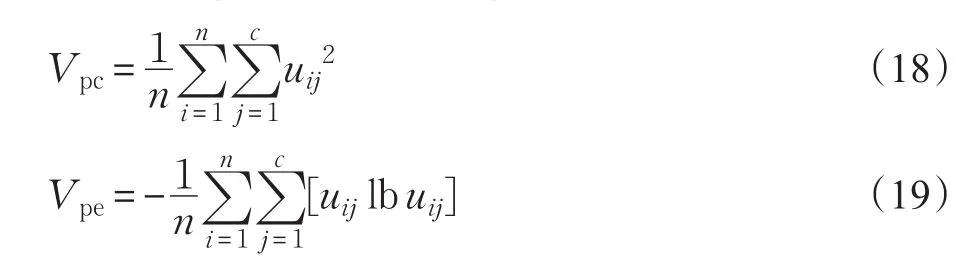
这种评价函数的思想在于如果模糊聚类效果越好，模糊度越大，得到的分割系数就越大，而分割熵越小。表1是几种算法使用9%的噪声图像进行试验的定量比较，从表中可以看出该算法在模糊聚类的定量分析上，效果是最好的。

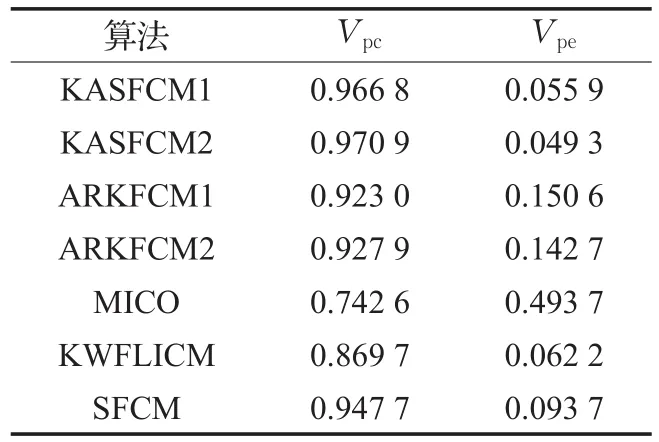
表1 不同算法的评价函数值比较

另外，分割的精度是衡量分割算法优劣程度的重要标准，分割精度越高，说明分割的准确性越高，反之同理。采用Jaccard系数来定量评价分割效果，在图像噪声强度为9%的情况下进行实验，结果如表2所示。可以看出，本文算法在白质和灰质的分割精度上都优于其他同类算法，尤其在灰质的分割精度上，精度有较大的提升。Jaccard系数定义如下：

其中A是真实图像，B是分割后的图像。

为了充分说明本文方法的鲁棒性以及平滑性，在图像上加入10%的莱斯（Rician）噪声进行比较，图4是几种方法的实验结果展示，红色矩形方框内的图像是经过处理局部放大的效果。可以看出，在针对Rician噪声鲁棒性和平滑性方面，本文的算法均比其他同类算法的效果明显，同样对于KWFLICM算法，尽管去噪效果很好，但是细节保留能力较差。

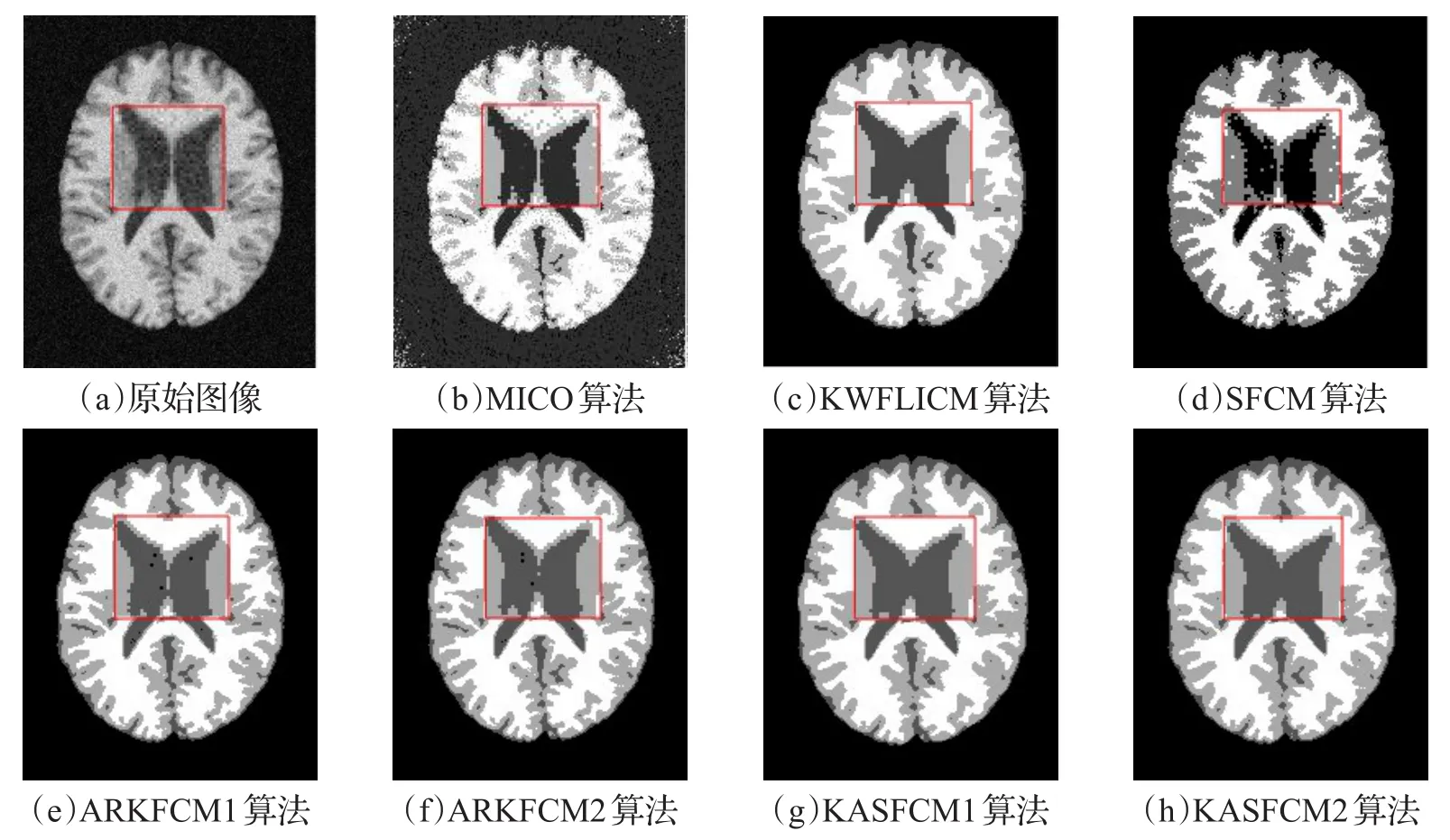
图410 %莱斯噪声图像使用不同算法分割结果

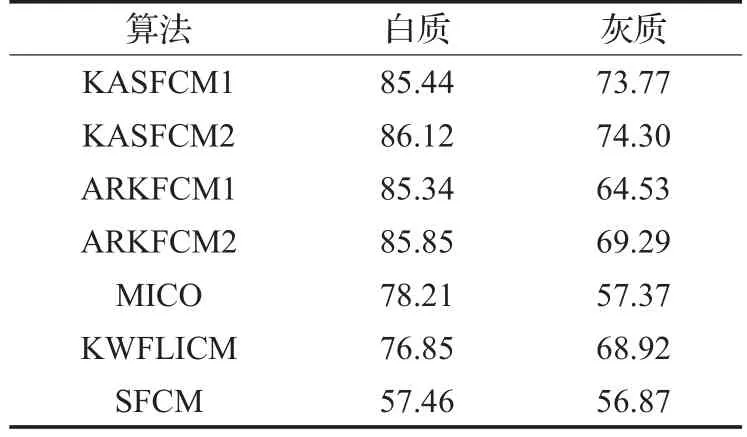
表2 不同算法Jaccard值比较%

5 结束语

通过引入核距离以及隶属度惩罚项，使得算法对噪声的鲁棒性更强，并且使用一种自适应正则化参数，使参数同时控制隶属度约束项以及邻域空间限制项，达到了减少参数的目的，同时引入空间信息，使本文的算法分割效果更加平滑，实验表明，在9%的噪声强度和10%Rician噪声下，本文的算法与其他同类算法比较，在分割精度、去噪、平滑性以及细节保留方面效果均有所提高。

[1] Jiang C F，Chang C C，Huang S H.Regions of interest extraction fromspect images for neural degeneration assessmentusingmultimodalityimagefusion[J].Multidimensional Systems and Signal Processing，2012，23（4）：437-449.

[2] Ji Z X，Sun Q S，Xia D S.A modified possibilistic fuzzy c-means clustering algorithm for bias field estimation and segmentation of brain MR image[J].Computerized Medical Imaging&Graphics，2011，35（5）：383-397.

[3] Nguyen T M，Wu Q M J.A fuzzy logic model based Markov random field for medical image segmentation[J].Evolving Systems，2013，4（3）：171-181.

[4] Liu C，Zhang X，Li X，et al.Gaussian kernelized fuzzy cmeans with spatial information algorithm for image segmentation[J].Journal of Computers，2012，7（6）.

[5] Bezdek J C.Pattern recognition with fuzzy objective function algorithms[M].New York：Plenum Press，1981.

[6] Li C，Gore J C，Davatzikos C.Multiplicative intrinsic component optimization（MICO）for MRI bias field estimation and tissue segmentation[J].Magnetic Resonance Imaging，2014，32（7）：413-439.

[7] Chuang K S，Tzeng H L，Chen S，et al.Fuzzy c-means clustering with spatial information for image segmentation[J].Computerized Medical Imaging&Graphics the Official Journal of the Computerized Medical Imaging Society，2006，30（1）：9-15.

[8] Ahmed M N，Yamany S M，Mohamed N，et al.Amodified fuzzy c-means algorithm for bias field estimation and segmentation of MRI data[J].IEEE Transactions on Medical Imaging，2002，21（3）：193-199.

[9] Chen S，Zhang D.Robust image segmentation using FCM with spatialconstraints based on new kernel-induced distance measure[J].IEEE Transactions on Systems Man&Cybernetics Part B Cybernetics A Publication of the IEEE Systems Man&Cybernetics Society，2004，34（4）：1907-1916.

[10] Krinidis S，Chatzis V.A robust fuzzy local information c-means clustering algorithm[J].IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society，2010，19（5）：1328-1337.

[11] Gong M，Liang Y，Shi J，et al.Fuzzy c-means clustering with local information and kernel metric for image segmentation[J].IEEETransactionsonImageProcessing A Publication of the IEEE Signal Processing Society，2013，22（2）：573-584.

[12] Elazab A，Wang C，Jia F，et al.Segmentation of brain tissues from magnetic resonance images using adaptively regularized kernel-based fuzzy c-means clustering[J].Computational&Mathematical Methods in Medicine，2015，2015：1-12.

[13] Wang X Y，Zhang D D，Wei N.Fractal image coding algorithm using particle swarm optimisation and hybrid quadtree partition scheme[J].Iet Image Processing，2015，9（2）：153-161.

[14] Wang X Y，Chen Z F，Yun J J.An effective method for color image retrieval based on texture[J].Computer Standards&Interfaces，2012，34（1）：31-35.

[15] Hofmann T，Schölkopf B，Smola A J.Kernel methods in machine learning[J].Annals of Statistics，2008，36（3）：1171-1220.

[16] Rsouza C.Kernel functions for machine learning applications[EB/OL].（2010-03）.http：//crsouza.com/2010/03/kernel-functions-for-machinelearning-applications/.

[17] Bezdek J C.Cluster validity with fuzzy sets[J].Journal of Cybernetics，1973，3（3）：58-73.

[18] Bezdek J C.Mathematical models for systematic and taxonomy[C]//Proceedings of Eigth International Conference on Numerical Taxonomy，San Francisco，1975：143-166.

ZHAO Haifeng,XIA Guofeng,SONG Weiming,et al.Brain MR image segmentation under strong noise interference.Computer Engineering andApplications,2018,54（6）：183-187.

ZHAO Haifeng,XIAGuofeng,SONG Weiming,ZHANG Shaojie

School of Computer Science and Technology,Anhui University,Hefei 230601,China

MRI（Magnetic Resonance Imaging）is easily affected by noise,and it has poor contrast along boundaries.MRI of brain tissue segmentation under the strong noise has always been a difficult problem,and it has attracted much attention.This paper puts forward a kind of algorithm using adaptive regularization parameters combined with spatial relation,which replaces the Euclidean distance by the Kernel distance for calculation,and segments the MR image under the strong noise,the robustness of segmentation is greatly improved.The main advantage is to define adaptive parameters for each point,and puts the parameters into two expressions of the objective function.And it not only reduces the number of parameters,but also enhances the segment result.Finally,combined with spatial relation,the segmentation is more accurate.The experiments show the proposed method improves the segmentation accuracy,detail retention and noise processing in brain.

Magnetic Resonance Imaging（MRI）;adaptive parameter;kernel distance;spatial relation

核磁共振图像（Magnetic Resonance Imaging）容易受到噪声的干扰，并且在图像边缘部分呈弱对比度。强噪声下核磁共振图像的脑组织分割一直是个难题，引起很多学者的关注。提出了一种使用自适应正则化参数并结合空间关系的算法，同时将核距离替换传统的欧式距离进行计算，对强噪声下的核磁共振图像进行分割，大大提高了分割的鲁棒性。算法的主要优点是为图像每个点定义自适应参数，并且将这个参数同时应用到目标函数的两项表达式当中，既减少了参数数量，又增强了分割效果。最后，由于结合空间关系，使分割结果更加的精确。实验表明，该方法在脑组织的分割精度、细节保留以及噪声处理方面比其他方法有所提高。

核磁共振图像；自适应参数；核距离；空间关系

2016-11-01

2017-01-13

1002-8331（2018）06-0183-05

A

TP391

10.3778/j.issn.1002-8331.1611-0032

国家自然科学基金（No.61300057，No.61402002）；国家高技术研究发展计划（863）子项目（No.2014AA0154104）；安徽省自然科学基金（No.1408085QF120，No.1408085MKL94）；教育部留学回国启动资金（教外司留[2014]1685号）。

赵海峰（1972—），男，博士研究生，副教授，主要研究领域为医学图像处理与应用、模式识别等；夏国峰（1990—），男，硕士研究生，主要研究领域为医学图像处理，模式识别等，E-mail：mapletter@126.com；宋维明（1991—），男，硕士研究生，主要研究领域为稀疏表示，模式识别等；张少杰（1982—），女，博士研究生，讲师，主要研究领域为模式识别，人机交互，虚拟现实等。