随机森林在滚动轴承故障诊断中的应用

张钰，陈珺，王晓峰，刘飞，周文晶，王志国

1.江南大学自动化研究所轻工过程先进控制教育部重点实验室，江苏无锡214122

2.西门子中国研究院，北京100000

随机森林在滚动轴承故障诊断中的应用

张钰1，陈珺1，王晓峰2，刘飞1，周文晶2，王志国1

1.江南大学自动化研究所轻工过程先进控制教育部重点实验室，江苏无锡214122

2.西门子中国研究院，北京100000

CNKI网络出版：2017-02-28,http://kns.cnki.net/kcms/detail/11.2127.TP.20170228.1820.006.html

1 引言

据统计，在工业生产中，在滚动轴承的旋转机械设备中，有30%的故障都是由滚动轴承的损伤所引起的。一旦旋转机械设备发生故障，其结果往往会造成严重的经济损失和安全事故。因此，对滚动轴承的故障诊断有着重要的研究意义[1]。

近些年来，国内外一些学者针对滚动轴承的故障诊断进行了许多研究，并取得了一定的成果。研究内容主要涉及特征提取和状态识别两个方面。针对滚动轴承故障的特征提取，通常利用振动传感器采集滚动轴承的振动信号，然后提取时域特征、频域特征或时频特征作为轴承诊断的特征向量，其中使用较多的时域特征有均方根值、峭度值，而频域和时频特征通常需要进行信号变换如：小波变换、快速傅里叶变换和经验模态分解。最后通过状态识别方法进行故障诊断，其中常用的识别方法有人工神经网络（ANN）和支持向量机（SVM）。ANN具有较强的自学能力、适应性和非线性逼近能力等优点，已经应用到轴承故障诊断领域中[2-6]，但是ANN同时也存在着参数优化难、收敛速度过慢等缺点。而SVM作为比较经典的分类算法，克服了ANN收敛速度慢和过拟合的问题，因此，在轴承故障诊断领域得到了非常广泛的应用[7-10]。当然，其也有一定的缺陷，即存在处理大样本数据时能力不足以及解决多分类问题精度较低等困难。

在特征提取时，数据的多样性会导致数据本身对特征向量有所偏好，即同一种特征向量在不同数据下的诊断效果不是当前数据中最优的诊断结果。为此需要提取多种特征，但是，特征向量维数的增大，不一定有利于诊断结果的提高。随机森林（Random Forest）作为集成学习中比较经典的算法之一，能够解决ANN收敛速度过慢，容易陷于过拟合等问题，同时也能解决SVM处理大样本数据的能力不足的缺点。更重要的是随机森林能够集成多种特征向量，有效提高诊断的正确率。随机森林已广泛应用于网络故障诊断、文本挖掘和图像处理等领域[11-13]，但是，却少有将随机森林应用到轴承故障诊断领域中的研究报告。

首先，从轴承的振动信号中提取时域特征作为特征向量，然后，利用特征向量作为随机森林算法的输入对轴承进行故障诊断。最后，与其他的传统诊断算法相比较。结果表明，随机森林算法的诊断准确率明显高于其他诊断算法。因此，随机森林在轴承故障诊断领域中有着重要的研究意义。

2 bootstrap重采样方法

bootstrap自助重采样方法是美国Standford大学教授Efron为解决小样本试验评估问题提出的一种新的增广样本的统计方法[14]。bootstrap方法基本思想是：从容量为n的原始样本中进行有放回的重复采样，采样样本的容量也为n，每个观测对象被抽到的概率为1/n，每次采样构成的子样本称为bootstrap样本。采样次数根据计算量而定。从每个重采样的样本中可以计算某个统计量的bootstrap分布，比如说均值，多个重采样样本的均值构成了原始样本均值的bootstrap分布。其过程一般可用随机数或者计算机输出n个0～1之间的随机数实现。即：先将样本变量编码为1,2,…,n；然后取分组距离1/n将区间[0,1]分成n个互斥的分隔：

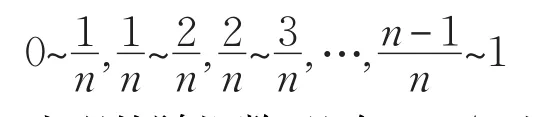
出现的随机数，凡在0～1/n之间的去编码“1”变量，凡在1/n～2/n之间的去编码“2”变量，…，凡在(n-1)/n～1之间的去编码“n”变量。

bootstrap重采样是集成学习算法对原始样本进行采样的方法，也是随机森林算法的一个重要构成部分。

3 分类与回归树（CART）

决策树是一种树状预测模型，它代表的是对象属性与对象值之间的一种映射关系。树的根节点是整个数据集的空间，树中每个节点表示某个对象，而每个分叉路径则代表某个可能的属性值，从根节点到该叶节点所经历的路径则是相应对象的预测值。决策树学习的目的是为了产生一棵泛化能力强的决策树。决策树的种类有很多，主要有ID3、C4.5和CART。如何选择划分属性是决策树中一个重要问题。ID3和C4.5分别采用信息增益和信息增益率作为划分属性，信息增益准则会对可取值数目较多的属性有所偏好，虽然C4.5克服了ID3的缺点，但是ID3和C4.5都存在生成的决策树分支复杂、规模较大、效率较低等问题。为了简化决策树的规模，提高生成决策树的效率，Breiman等人提出了CART[15]。

CART决策树是一种结构简单的二叉树，与ID3和C4.5决策树相比，采用一种二分递归分割的技术，有着更好的划分能力，可用于分类和回归任务。CART决策树使用“基尼指数”来选择划分属性，数据集的纯度可用基尼值表示如下：

从式（1）中可以看出基尼值反映了从数据集中随机抽取两个样本，其类别标记不一致的概率。因此，数据集的纯度与基尼值的大小成反比。其中属性a的基尼指数定义为：

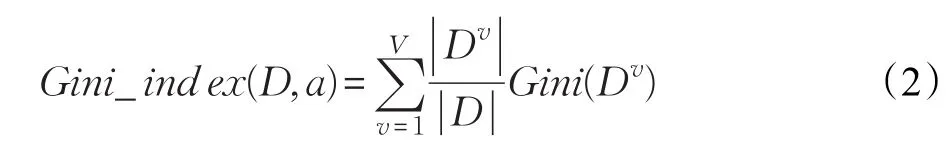
因此，在候选属性集合中，选择使得划分后基尼指数最小的属性作为最优划分属性。由于CART具有结构简单、良好的划分能力等特点，使其成为集成学习算法中最为常见的基学习器。

4 随机森林算法

随机森林由Breiman在2001年提出的[16]，随机森林由多个决策树构成，通过多个决策树的投票原则来决定最终的结果。具体过程分为两步：第一步是利用bootstrap方法重采样，从容量为S的原始样本集中随机选择S个样本组成bootstrap样本集，分别利用多个不同的bootstrap样本集训练多个决策树。第二步是在构造决策树时，从特征属性集中随机选择一个包含m个属性的子集，然后在再利用这个子集中的属性进行划分。研究表明[11]，随机森林可以有效地提高分类精度。

4.1 随机森林定义

定义1（随机森林）随机森林是由多个决策树{h(x,Θk),k=1,2,…,n}组成的分类器，其中{}Θk是相互独立且同分布的随机向量，最终由所有决策树综合投票决定输出结果。

4.2 随机森林收敛性

给定k个分类器h1(x),h2(x),…,hk(x)和随机向量Y,X，定义边缘函数：

其中，I(∗)是示性函数，该边缘函数刻画了对向量Y,X正确分类的平均得票数超过其他任何类平均得票数的程度。可知，边缘越大分类的置信度就越高。分类器的泛化误差表示如下：

在随机森林中，hk(X)=h(X,Θk)。对于随机森林中的树的数目较大，可以用大数定律和树的结构得到如下定理：

定理1随着树的数目增加，对所有随机向量Θ,…,PE*趋于

文献[11]已给出定理1的证明，并且表明随机森林不会随着树的数量增加而出现过拟合，泛化误差将收敛于某一个上界。

定义2随机森林的边缘函数

分类器{h(X,Θ)}的分类强度

假设s≥0，根据切比雪夫不等式，可得：

不等式具有以下形式：

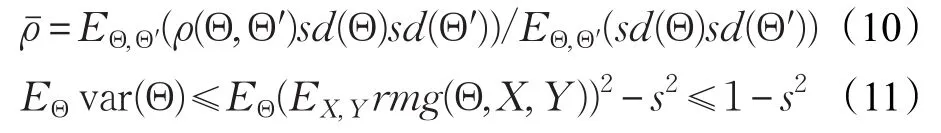
由式（4）、（9）和（11）得到以下结论。

定理2随机森林的泛化误差上界的定义为：

由定理2可知，随机森林的泛化误差上界由每棵决策树的分类强度（精度）和树与树之间的相关程度所决定。泛化误差上界随着随机森林中树与树之间的相关程度增大而增大，并且泛化误差上界也与每棵树的分类强度成正比。

4.3 随机森林算法流程

随机森林利用分类与回归树（CART）进行单个分类树的生长，生成的分类树与传统的CART有所区别，不进行裁剪，使树最大化地生长。随机森林生成的具体步骤如下：

（1）随机森林每次利用bootstrap重采样方法从原始训练样本集中抽取63.2%的样本生成一个子样本集，每一个子样本对应着一棵分类树。同时，原始样本没有被抽中的样本称为袋外数据OOB（Out-Of-Bag），OOB数据被用来评估分类器的分类正确率[17]。

（2）利用每个子样本集，生长为单棵分类树。在树的每个节点处，从M个特征向量中随机挑选m个特征向量，根据Liaw给出的经验公式[18]，通常取m=int(M)，即m取M的向下整数。按照节点不纯度最小的原则从这m个特征向量中选出一个特征α作为该节点的分类属性。

（3）根据特征α将节点分成2个分支，然后再从剩下的特征中寻找分类效果最好的特征，如此递归构造分类树的分支，使分类树充分生长，每个节点的不纯度达到最小，而不进行剪枝。直到这棵树能准确地分类训练集，或者所有属性使用完。

（4）在分类阶段，分类标签是由所有分类树的结果综合而成。随机森林使用的是投票原则。即：

其中，N是森林中决策树的数目，I(∗)是示性函数，nhi,c是树hi对类C的分类结果，nhi是树的叶子节点数。

5 基于随机森林的轴承故障诊断

5.1 SQI-MFS实验平台

如图1所示，SQI-MFS实验平台由电机、变频器、轴承、底座支撑架组成。其中轴承型号为MB ER-16K，实验平台可以模拟各类健康或故障轴承在不同转速和不同负载下的运行状态。

图1 SQI-MFS实验平台

如图2所示，从左至右、从上至下，分别为健康轴承、滚珠故障轴承、内圈故障轴承以及外圈故障轴承的实物图。

5.2 SQI-MFS实验平台数据

本实验采集了36种运行状态下的振动数据，分别为：3种负载大小（转子负载个数）（0，1，3）×3种转速（r/m）（600，1 200，1 800）×4种轴承（健康，滚珠故障，内圈故障以及外圈故障轴承），将数据分别按负载大小（3种）和电机转速（3种）分成9组。其中故障轴承的故障点大小为19.05 mm。图3～图6分别是其中一组轴承的4种状态下的振动信号图。

图24 种状态的轴承实物图

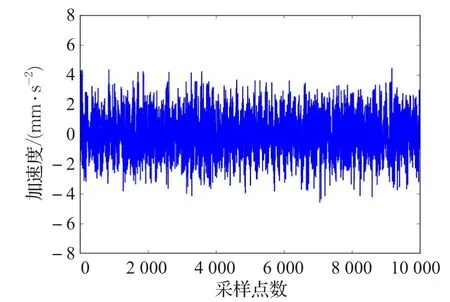
图3 健康轴承振动信号图

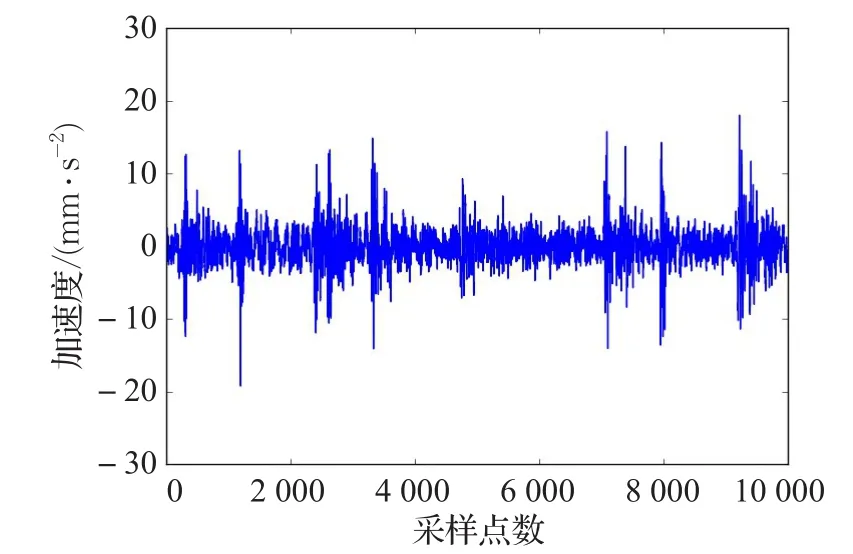
图4 滚珠故障轴承振动信号图

图5 内圈故障轴承振动信号图

5.3 特征提取

由于随机森林算法中需要从M个特征向量中选取m个特征向量，若将M设置为1，随机森林算法的特点就无法表现出来。另外，为了体现随机森林能够在比较简单的特征向量条件下，就能表现出其较好的性能。这里提取轴承振动信号的时域特征[19]。时域特征向量有：最大值F1，均方根值F2，歪度值F3，峭度值F4，波性指标F5，脉冲指标F6，歪度指标F7，峰值指标F8，裕度指标F9，峭度指标F10。

图6 外圈故障轴承振动信号图

5.4 轴承的故障诊断

将上述10种特征向量组合成为一种特征向量F=[F1,F2,…,F10]，并将对应轴承的健康、滚珠故障、内圈故障和外圈故障四种状态分别标上标签C=[0,1,2,3]，作为分类器的输入，采用十折交叉验证计算诊断的正确率。其中，SVM的核函数为高斯径向基函数，BP神经网络的隐含层神经元个数为21，根据多次试验，发现kNN算法中k值取5，效果较好。此外，对于SVM和kNN算法，分别将特征向量F中每个特征向量Fi(i=1,2,…,10)作为二者的输入，最后比较这些分类器的诊断正确率，找出其中最大的正确率作为最终的诊断结果，并且将这些正确率最大的特征向量称为“最优的特征向量”（BP神经网络中最优的特征向量均为F）。

如图7所示，是SQI-MFS所有轴承数据中OOB错误率收敛最慢的一条曲线。从图7可以看出，随机森林中决策树的个数在500左右时，OOB错误率已经趋于平稳，为了保证所有的轴承数据正确率达到稳定，分类器的数量取最大值500。

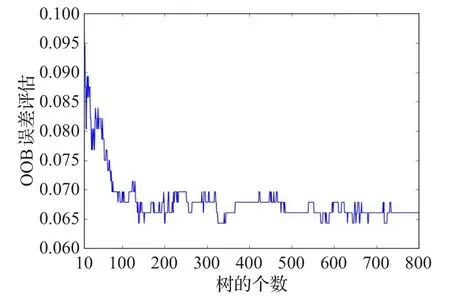
图7 OOB错误率与树数量的关系（SQI-MFS数据）

6 实验结果

6.1 传统分类器诊断结果

如表1和表2所示，是针对SQI轴承的9组数据，在SVM和kNN两种分类器下的正确率。可以看到对于不同的数据，在算法相同情况下，最优的特征向量不同，其中，对于SVM分类器，9组数据中最优次数最多的特征向量是F4（峭度值），而对于kNN分类器最优次数最多的特征向量是F2（均方根值）。另外，对于不同的分类器，在数据相同的情况下，最优的特征向量也不一致。同时，可从表1、表2中看出，在所有最优的特征向量中，只出现了单一的特征向量，组合之后的特征向量F=[F1,F2,…,F10]并没有出现。说明对于SVM和kNN分类器，输入的特征向量过多时，其分类的精度不一定得到提高。

表1 SVM对SQI轴承的诊断结果

表2 kNN对SQI轴承的诊断结果

6.2 随机森林诊断结果

由上述两种算法分析结果可知，若是利用同样的算法进行故障诊断时，最优的特征向量不一致，仅提取一种或者两种特征向量，其诊断结果的可信度会比较低，另外，不同的分类器对特征向量的偏好也不一样。而随机森林刚好可以弥补这两个缺点。随机森林中有多个分类器（决策树），每个分类器的参数不一样，并且，每个分类器的训练样本集也不一样，因此，就会产生多个差异化的分类器，使每个分类器的诊断结果不一致。最终，通过投票的形式产生最终的分类结果。这样会有效地提高诊断的正确率。如表3所示，针对SQI轴承的9组数据进行对比实验，在SQI轴承诊断结果中，可以看到。除了第9组数据kNN的正确率高于BP神经网络和CART算法，其他各组数据的诊断效果，随机森林均略好于BP神经网络和CART算法，且诊断效果明显比SVM和kNN要好。与CART算法相比，可以看到，随机森林由于采用了组合CART的形式，比单个CART的诊断效果要有所提高。

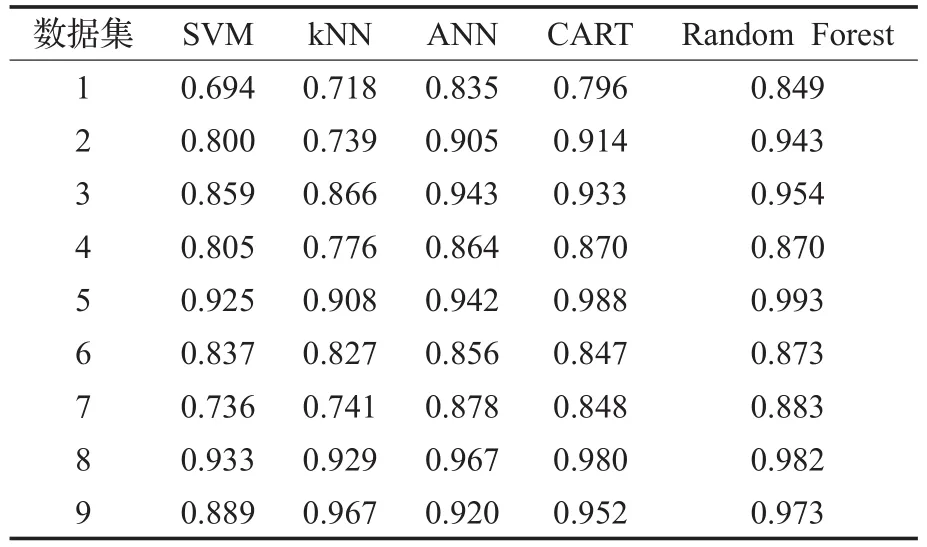
表3 SQI轴承的诊断对比结果

7 结束语

本文中，提出了基于随机森林的轴承故障诊断方法，利用SQI实验平台轴承数据进行多种算法的对比性试验，与传统的分类器SVM和kNN相比，随机森林的诊断正确率提高了0.05～0.17，并且，不需要根据不同的轴承数据而提取不同的特征向量进行诊断；与人工神经网络（BP神经网络）相比，随机森林的诊断正确率可以提高0.004～0.05，而且不需要进行繁琐的参数寻优过程。不同的分类器对于相同的样本集有着不同的分类性能。随机森林通过将简单的弱分类器（决策树）的分类结果集成起来，从而达到提高精度的效果。因此，随机森林在轴承故障诊断方面有着较好的实际推广意义。

[1] 王泽文.基于振动信号的滚动轴承故障诊断与预测系统研究[D].江苏徐州：中国矿业大学，2014.

[2] Subrahmanyam M，Sujatha C.Using neural networks for the diagnosis of localized defects in ball bearings[J].Tribology International，1997，30（10）：739-752.

[3] Li B，Chow M Y，Tipsuwan Y，et al.Neural-network-based motor rolling bearing fault diagnosis[J].IEEE Transactions on Industrial Electronics，2000，47（5）：1060-1069.

[4] Zhang Y Q，Zhang P L，Wu D H，et al.Bearing fault diagnosis based on optimal generalized S transform and pulse coupled neural network[J].Journal of Vibration&Shock，2015，34（9）：26-31.

[5] Sreejith B，Verma A K，Srividya A.Fault diagnosis of rolling element bearing using time-domain features and neural networks[C]//IEEE Region 10 and the Third International Conference on Industrial and Information Systems，2008：1-6.

[6] Yu Y，Yu Dejie，Cheng J.A roller bearing fault diagnosis method based on EMD energy entropy and ANN[J].Journal of Sound&Vibration，2006，294（1/2）：269-277.

[7] Yang M，Chen J.Rolling element bearing fault diagnosis based on slice spectral correlation density and support vector machine[J].Journal of Vibration&Shock，2010，29（1）：196-199.

[8] Ma J，Wu J D，Fan Y G，et al.Fault diagnosis of rolling bearing based on the PSO-SVM of the mixed-feature[J].Applied Mechanics&Materials，2013，380-384：131-134.

[9] Wu Husheng，Lv Jianxin，Lai L H，et al.Fault pattern recognition of rolling bearing based on EMD-SVD model and SVM[J].Noise&Vibration Control，2011，31（2）：89-93.

[10] Shi R M，Yang Z J.Application of optimized directed acyclic graph support vector machine based on complex network in fault diagnosis of rolling bearing[J].Journal of Vibration&Shock，2015，34（12）：1-6.

[11] Masetic Z，Subasi A.Congestive heart failure detection using random forest classifier[J].Computer Methods&Programs in Biomedicine，2016，130：54-64.

[12] Zhang H W，Wang M W，Gan L X.Automatic text classification model based on random forest[J].Journal of Shandong University，2006，41（3）：139-143.

[13] Zhuang J F，Luo J，Peng Y Q，et al.Fault diagnosis method based on modified random forests[J].Computer Integrated Manufacturing Systems，2009，15（4）：777-785.

[14] Efron B.Bootstrap methods：Another look at the jacknife[M]//Breakthroughs in statistics.New York：Springer，1979：1-26.

[15] Breiman L I，Friedman J H，Olshen R A，et al.Classification and Regression Trees（CART）[J].Biometrics，1984，40（3）：17-23.

[16] Breiman L.Random forest[J].Machine Learing，2001，45（1）：5-32.

[17] Cutler A，Cutler D R，Stevens J R.Random forests[J].Machine Learning，2011，45（1）：157-176.

[18] Bauer E，Kohavi R.An empirical comparison of voting classification algorithms：Bagging，boosting，and variants[J].Machine Learning，1999，36（1/2）：105-139.

[19] Ali J B，Saidi L，Chebel-Morello B，et al.A new enhanced feature extraction strategy for bearing remaining useful life estimation[C]//International Conference on Sciences and Techniques of Automatic Control and Computer Engineering，2015.

ZHANG Yu,CHEN Jun,WANG Xiaofeng,et al.Application of random forest on rolling element bearings fault diagnosis.Computer Engineering and Applications,2018,54（6）：100-104.

ZHANG Yu1,CHEN Jun1,WANG Xiaofeng2,LIU Fei1,ZHOU Wenjing2,WANG Zhiguo1

1.Key Laboratory of Advanced Process Control for Light Industry,Ministry of Education,Institute of Automation,Jiangnan University,Wuxi,Jiangsu 214122,China
2.Siemens China Institute,Beijing 100000,China

Due to selection difficulties for different bearing data feature,and low accuracy problems of single classifier method in the fault diagnosis of rolling bearing,this paper proposes a rolling bearing fault diagnosis algorithm with random forest based on Classification And Regression Tree（CART）.Random forest is an ensemble learning method which contains a variety of classifiers.The accuracy of rolling bearing fault diagnosis is improved by“integrated”thought of random forest.First,time domain statistical indicators are extracted from the vibration signals of rolling bearings and will be used as feature vectors.Then,the random forest algorithm is utilized for the fault diagnosis of rolling bearing.Compared with the traditional algorithm（SVM,kNN and ANN）and single CART,diagnostic results proposed in this paper indicate that random forest algorithm has high diagnostic accuracy by using the bearing data of SQI-MFS experimental platform.

rolling bearing;fault diagnosis;feature extraction;random forest

针对不同轴承数据特征选择困难和单个分类器方法在滚动轴承故障诊断中精度较低的问题，提出了一种基于分类回归树（CART）的随机森林滚动轴承故障诊断算法。随机森林是包含了多种分类器的集成学习方法。通过随机森林的“集成”思想来提高滚动轴承故障诊断的精度。从滚动轴承的振动信号中提取时域统计指标，将其作为特征向量，利用随机森林（Random Forest）对滚动轴承故障进行诊断。利用SQI-MFS实验平台的轴承数据，与传统分类器（SVM、kNN和ANN）以及单个分类回归树的诊断结果相比，随机森林算法具有比较高的诊断精度。

滚动轴承；故障诊断；特征提取；随机森林

2016-10-13

2016-12-01

1002-8331（2018）06-0100-05

A

TH17；TP39

10.3778/j.issn.1002-8331.1610-0127

国家自然科学基金（No.NSFC 61403167）。

张钰（1991—），男，硕士研究生，主要研究方向为基于数据挖掘的轴承故障诊断与寿命预测，E-mail：yuzhang_jndx@163.com；陈珺（1980—），女，博士，副教授，主要研究方向为复杂系统建模与分析。