基于概率密度函数的时滞依赖故障检测与诊断

陈龙，李涛，徐啸峰

南京信息工程大学信息与控制学院，南京210044

基于概率密度函数的时滞依赖故障检测与诊断

陈龙，李涛，徐啸峰

南京信息工程大学信息与控制学院，南京210044

CNKI网络出版：2017-04-14,http://kns.cnki.net/kcms/detail/11.2127.TP.20170414.1723.018.html

1 引言

随着科技的不断进步，现代控制系统的形式变得越来越复杂，而故障发生的比例也随之增长。控制系统一旦发生故障，就有可能造成整个系统的不稳定、失效，甚至人员和财产的巨大损失。为了避免故障的发生，或者将故障发生时带来的危害降到最低，人们不断研究新技术来应付故障系统，以保证系统能够安全、可靠地运行。因此，对控制系统进行故障检测与诊断研究，保障现代复杂系统的可靠性与安全性，具有十分重要的意义[1]。

近几年，随机系统是控制理论与控制工程领域中的一个重要的研究方向。经过国内外众多学者多年的深入研究，随机控制已形成较为系统和完善的理论体系。目前，随机系统控制研究的主要成果有马尔可夫参数过程控制[2]、最小方差控制[3]、自校正控制[4]和线性高斯二次型[5]等。但是，在这些传统的随机控制中，大都假设系统中随机变量的统计特性服从高斯分布，然而在实际应用中并非如此，大多统计特性是非高斯分布，往往都是要求过程变量的概率密度函数[6-7]。文献[8]提出了一种有理平方根B样条模型，并设计了一种线性随机系统的输出概率密度函数控制和建模方法。文献[9]基于有理平方根B样条模型中实际权重与伪权重的关系，提出了PDF的建模方法，并在此方法上设计了相应的控制器。文献[10]基于有理平方根B样条模型，设计了一种针对输出概率密度函数的预测控制算法，并设计了控制器。为了让随机系统更加可靠，对随机系统进行故障检测和诊断也越来越受到重视[11-15]。文献[16]利用PDF信息设计了一种基于观测器的故障检测方法。文献[17]基于输出概率密度函数和神经网络，通过设计自适应控制器提出了一种新的故障检测与诊断策略。这类设计方法具有很大的应用潜力，比如在矿物加工浮选工艺中，浮选过程表现出多变量、非线性等特点，而且浮选泡沫尺寸的非高斯分布、左偏斜、高峰值等分布特性，导致常规的方法无法准确检测和诊断浮选过程中出现的故障。文献[18]通过对泡沫尺寸分布的输出概率密度函数的统计分析，建立了非线性不确定性权动态模型，基于PDF设计了一种新的浮选过程故障检测和诊断方法。

另外，时滞现象广泛存在于现实的系统中，由于时滞的存在，得到的是被滞后了的控制信息，导致被控量不能及时控制信号动作，时滞是导致系统不稳定的一个重要原因[19]。数十年来许多学者对于时滞系统进行了深入的研究[20-24]。在随机分布系统的故障检测与诊断过程中考虑时滞的影响也是非常重要的。然而，目前关于随机分布系统时滞依赖的故障检测与诊断方法并不多。

因此，受到上述问题的启发，本文的主要目的是设计一个包含时滞信息的故障检测观测器和故障估计器，得到时滞依赖的故障检测与诊断方法。首先，针对一类包含时滞和建模误差的随机分布系统，建立基于PDF信息的残差，然后通过构造李雅普诺夫泛函，建立基于LMI时滞依赖的故障检测观测器的方法，进一步，在此基础上加入故障估计，设计了故障估计器的方法。最后，通过仿真实验，证明其有效性。

2 问题描述

这里的概率密度函数是利用有理平方根B样条函数[25]来描述的。假定随机系统在时刻t的输出η(t)∈[a,b]是一致有界的随机过程，u(t)为输入向量，F(t)为故障。则在任意时刻，η(t)的分布可以用它的概率密度函数γ(z,u(t),F(t))来描述，定义如下：

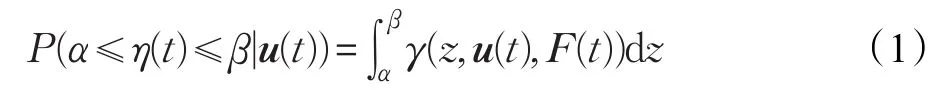
P(α≤η(t)≤β|u(t))表示系统在u(t)的作用下，输出z(t)落在区间[α,β]的概率。假设区间[a,b]已知，输出概率密度函数γ(z,u(t),F(t))连续且有界，则可以用如下的有理平方根B样条模型来逼近，并且在建模过程中考虑了建模误差：

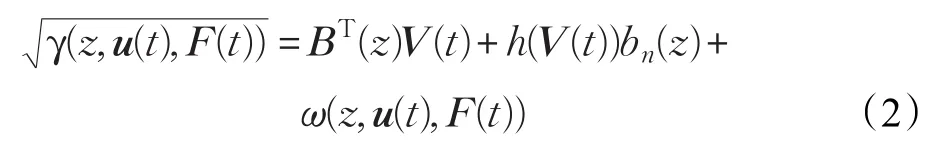
这里bi(z)(i=1,2,…,n)是预先给定的定义在区间[a,b]上的基函数，BT是与基函数相关的函数，V(t)为权值，，δ是给定的正数，并且给定矩阵U1，对于任意的V1(t)和V2(t)，成立。

假设B样条模型中权值V(t)与输入u(t)和故障F(t)之间满足如下的系统描述：

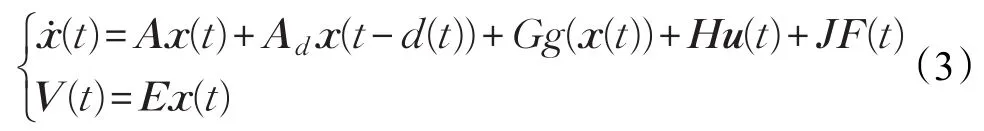
其中，x(t)是系统的状态，d(t)是时变时滞，F(t)是系统故障，A,Ad,G,H,J,E是具有合适维数的系统矩阵，其初值表示为x(t)=φ(t)(-τM≤t≤-τ0),τ0和τM表示常时滞。给定矩阵U2,对于任意x1(t)和x2(t),成立。

引理[26]对任意矩阵R＞0，对于x∈[α1,α2]，始终满足下列不等式：

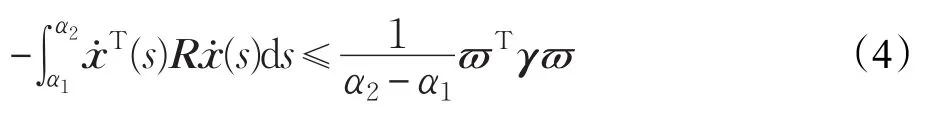
其中

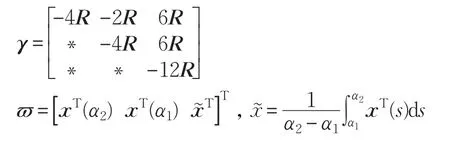
3 时滞依赖故障鲁棒检测观测器设计

故障检测主要是通过残差信号来进行检测的，为了产生残差，构造观测器如下：

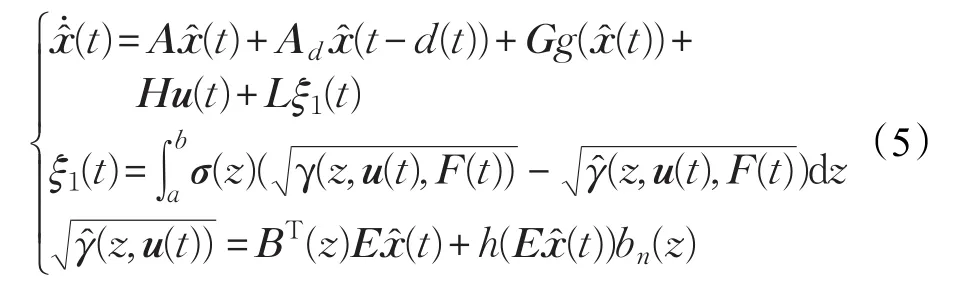
定义状态误差：

于是可得误差系统如下：

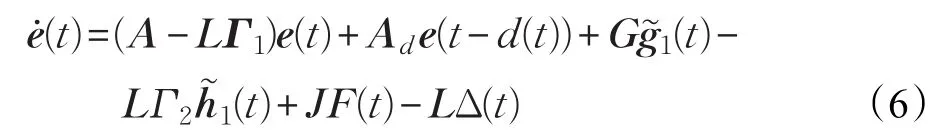
这里

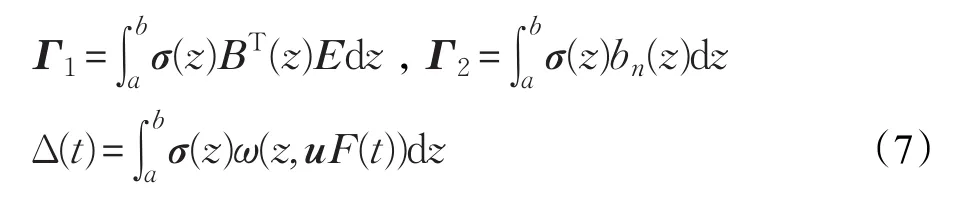
ξ1(t)可表示为：

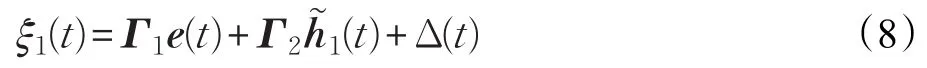
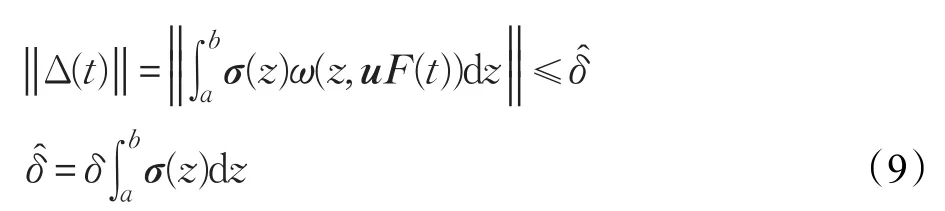
下面的定理给出了包含时滞信息及建模误差信息的故障观测器的设计方法。

定理1给定标量λi＞0(i=1,2)，时间τM＞τ0≥0，0＜ḋ(t)＜1，及αi(i=1,2,3,4,5,6)，如果存在矩阵P＞0，Q1＞0，Q2＞0，Q3＞0，S1＞0，S2＞0，R和任意可逆矩阵H1，标量η＞0，满足如下不等式：

其中

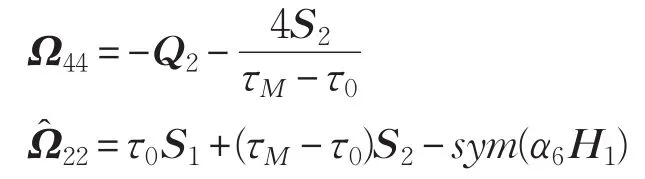
则不存在故障F(t)时，误差系统（6）是渐近稳定的，且对任意t∈[τ0τM]满足：

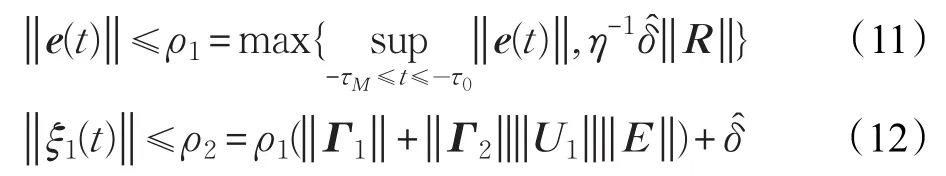
证明构造李雅普诺夫泛函为：

则：

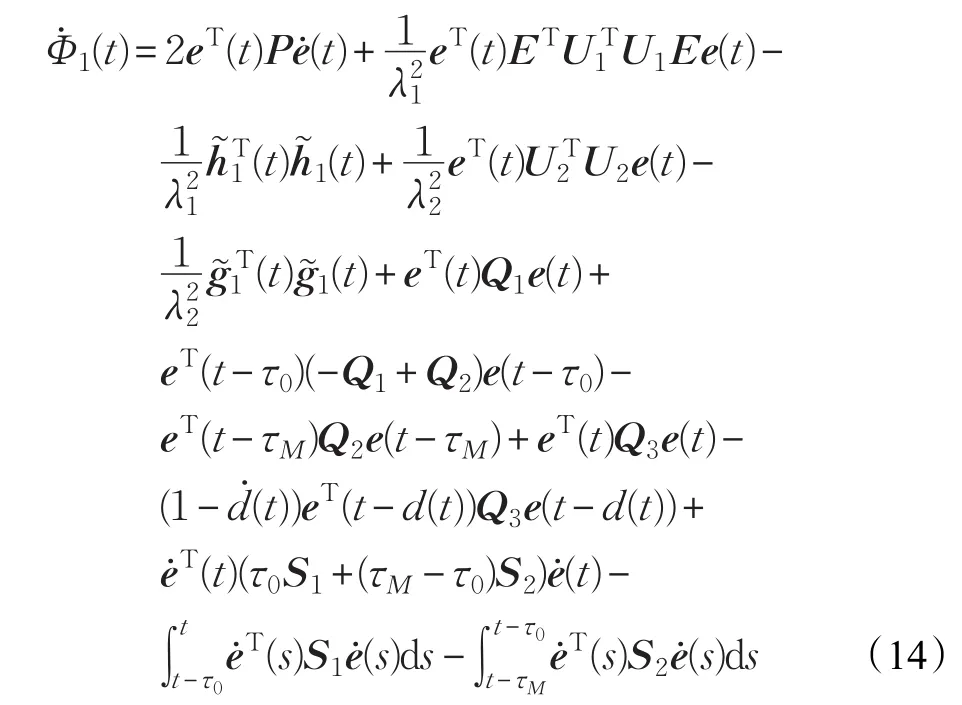
对于任意矩阵H，如下的等式恒成立：

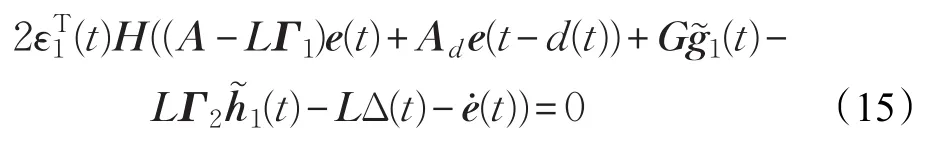
其中：

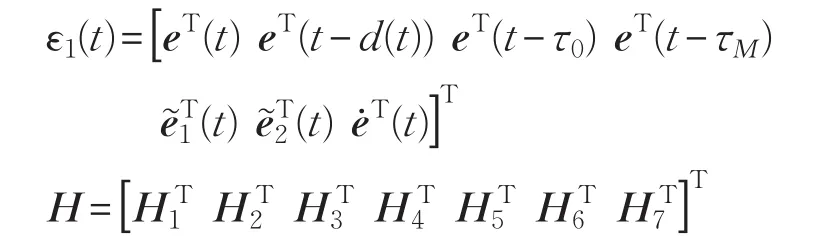
联合式（7）、（14）、（15），并令：H2=α1H1,H3=α2H1,H4=α3H1,H5=α4H1,H6=α5H1,H7=α6H1。

所以

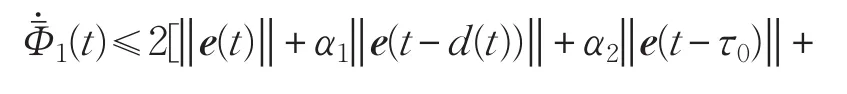
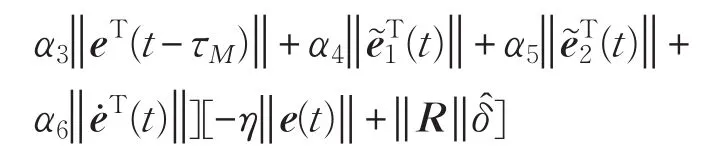
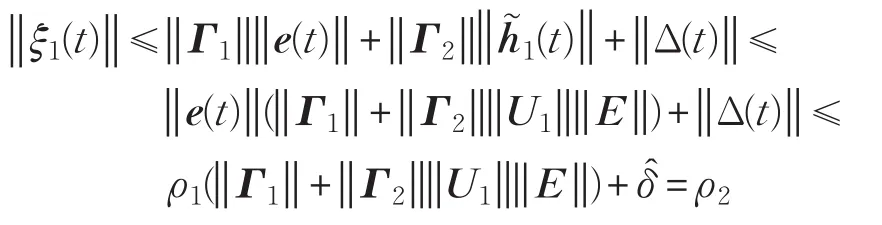
证明结束。

4 故障估计

为了估计故障的大小，设计故障估计器如下：

这里的F̂(t)是故障F(t)的估计值，γi(i=1,2)是待设计的故障估计增益量。可得到如下误差系统：

Γ1，Γ2和Δ(t)定义于式（7）。假设

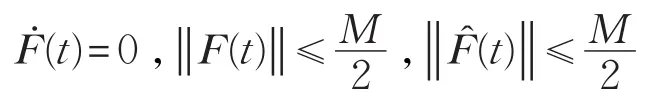
下面的定理提供一种故障F(t)的估计算法。

定理2给定标量λi＞0(i=1,2)，τM＞τ0≥0，0＜ḋ(t)＜1，αi(i=1,2,3,4,5,6,7)，如果存在矩阵P＞0，Q1＞0，Q2＞0，Q3＞0，S1＞0，S2＞0，R，γ1，γ2和任意可逆矩阵H1，标量μ＞0，κ＞0，满足如下不等式：

Ω见定理1。

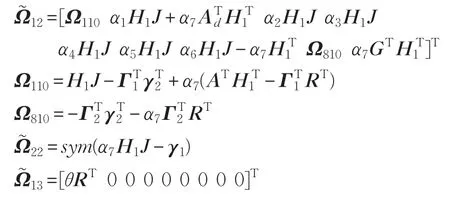
于是在故障估计器（16）的作用下，误差系统（17）是渐近稳定且对于任意t∈[τ0τM]满足：

证明构造李雅普诺夫泛函：

则

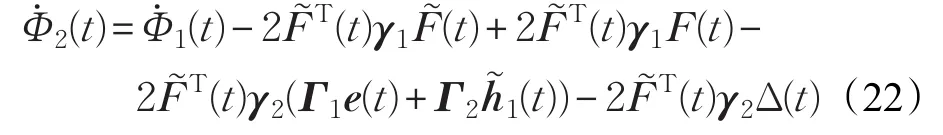
令：

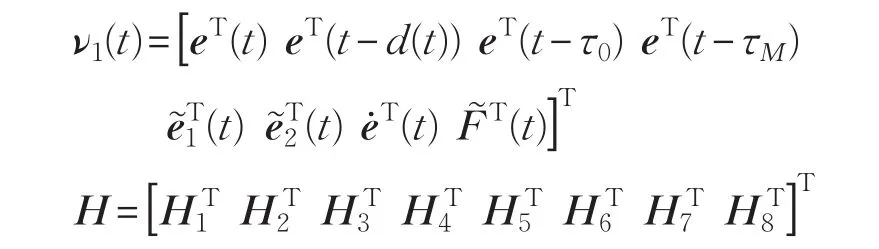
则

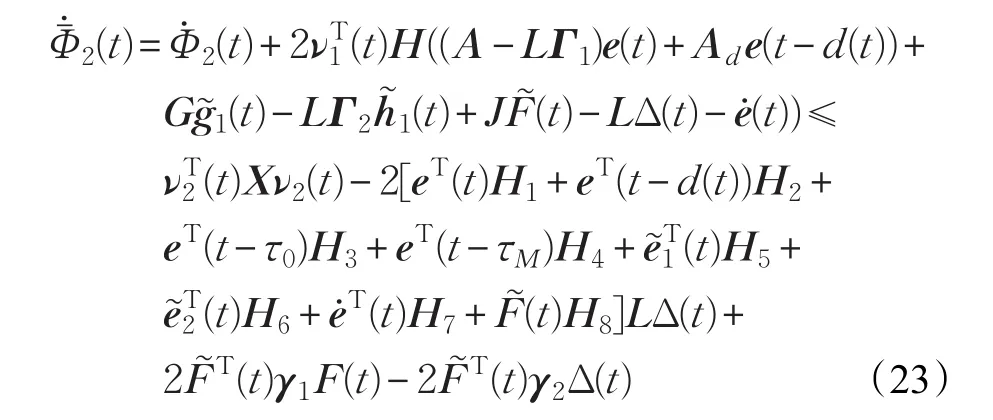
其中：

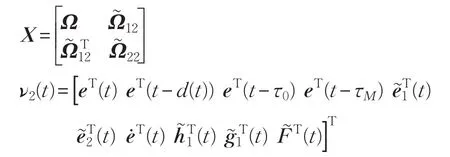
令：H2=α1H1,H3=α2H1,H4=α3H1，H5=α4H1，H6=α5H1，H7=α6H1，H8=α7H1。

则

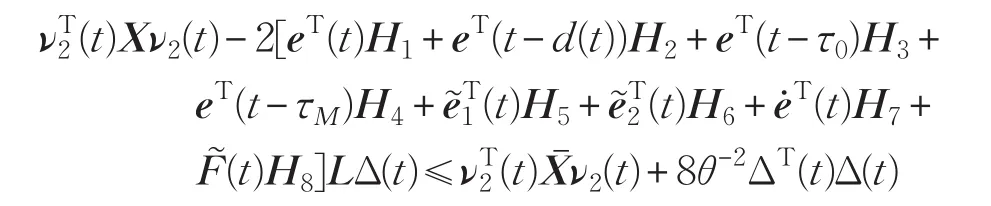
所以

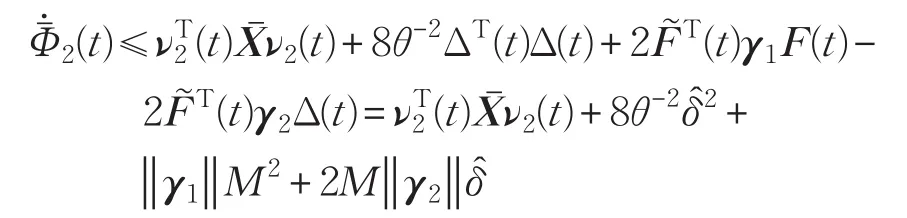
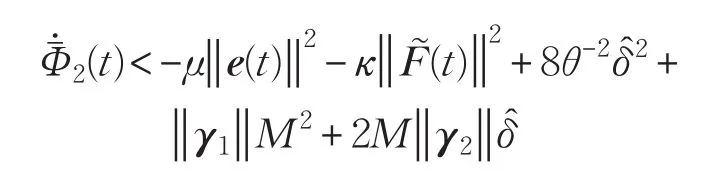
5 仿真实验

为了验证本文提出方法的有效性，本章在Matlab环境下对包含时滞和建模误差的随机分布系统进行仿真研究。假设输出概率密度函数可以用

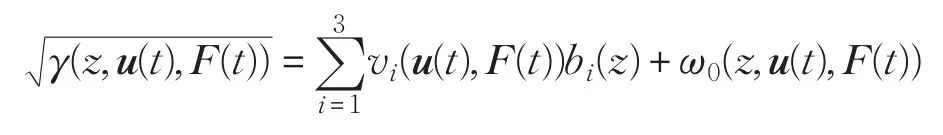
来逼近，这里的z定义于区间[0，1.5]，并且

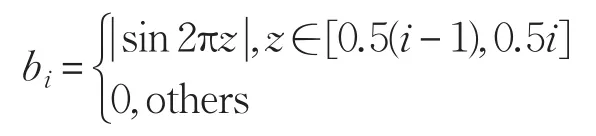
其中i=1,2,3。系统参数如下：

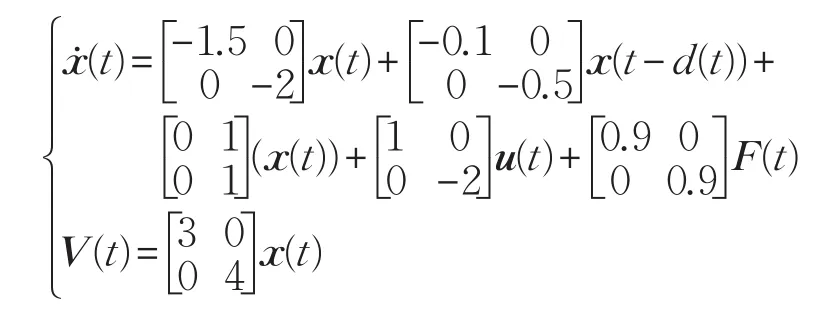
非线性函数的界分别为U1=diag{}0.1,0.1，U2=，计算得和Λ3=0.25。于是当σ(z)=1时可得Γ1=[0.954 9 1.273 2],Γ2=0.381 3。

设置初始状态为：

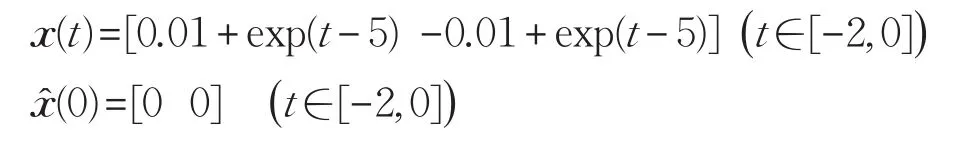
本文考虑如下故障：

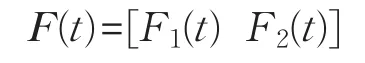
其中

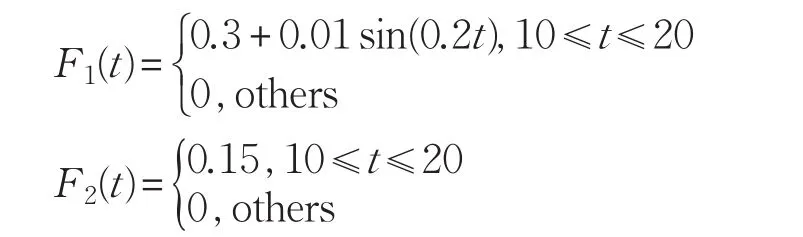
令λ1=1,λ2=1,ḋ(t)=0.1,τ0=0.01 s,并选取α1=α2=α3=α4=α5=α6=α7=0.1。当τM=0.02 s时，通过Matlab Toolbox求解定理1得到η=0.130 9，ρ2=0.040 0。

通过定理2得到：

图1至3描述的分别是当τ0=0.01 s,τM=0.02 s时，故障检测阈值与评估函数的响应，残差的响应，以及故障及故障估计的响应。

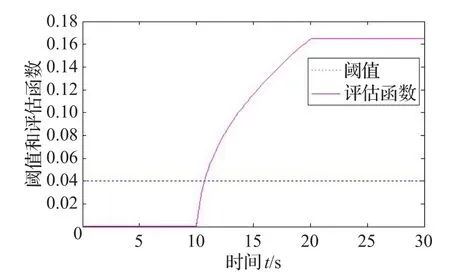
图1 τ0=0.01 s,τM=0.02 s时故障检测阈值与评估函数的响应

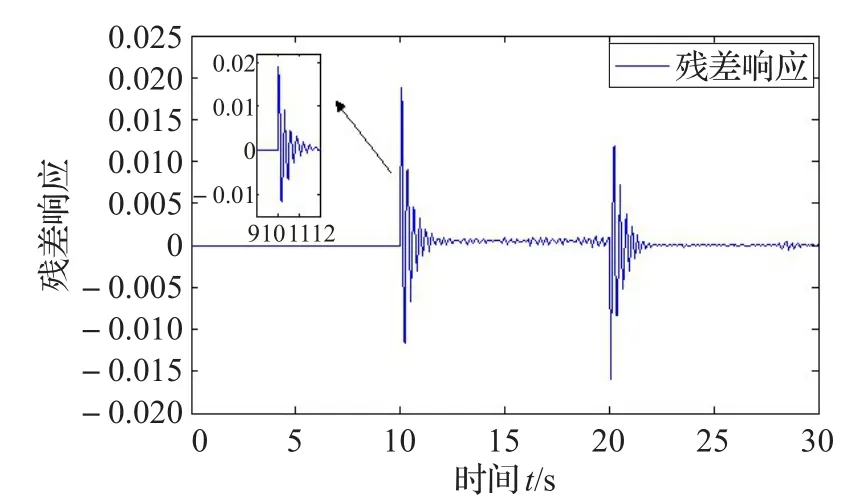
图2 τ0=0.01 s,τM=0.02 s时残差的响应

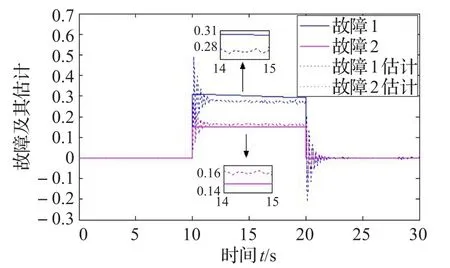
图3 τ0=0.01 s,τM=0.02 s时故障与故障估计的响应

当τM=0.2 s时，通过Matlab Toolbox求解定理1得到η=0.116 2，ρ2=0.041 2。

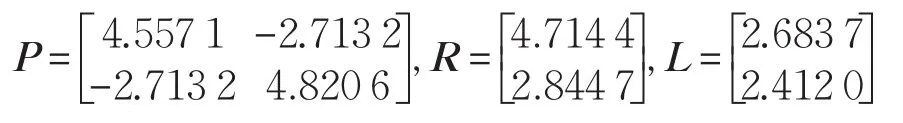
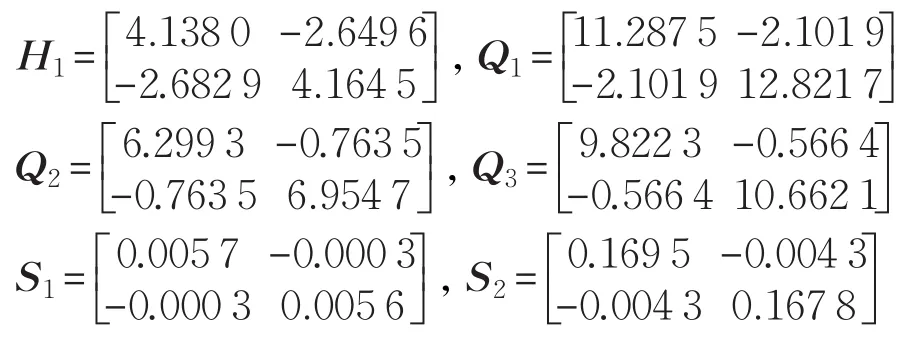
通过定理2得到：

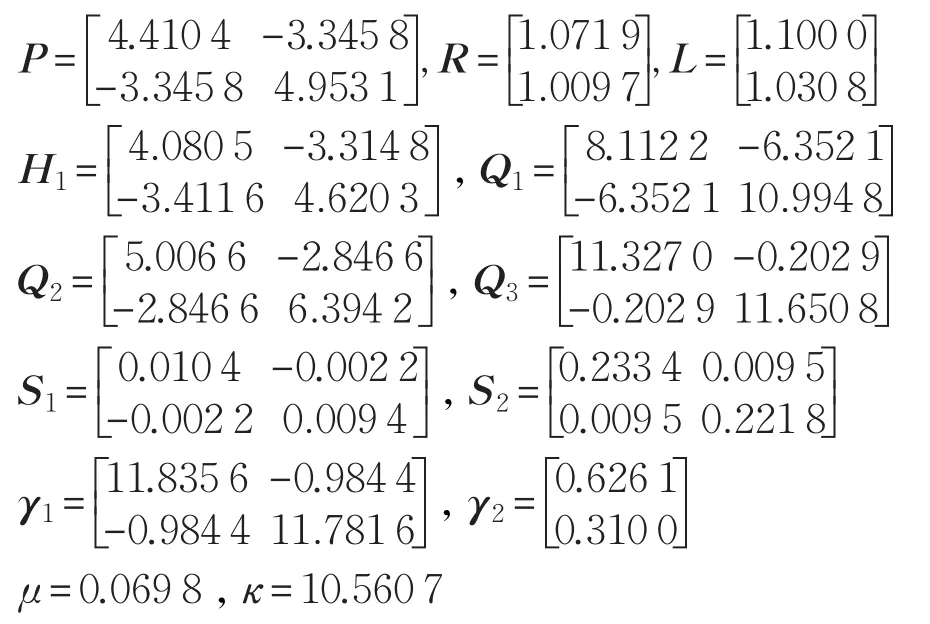
图4至6描述的分别是当τ0=0.01 s,τM=0.2 s时，故障检测阈值与评估函数的响应，残差的响应，以及故障及故障估计的响应。

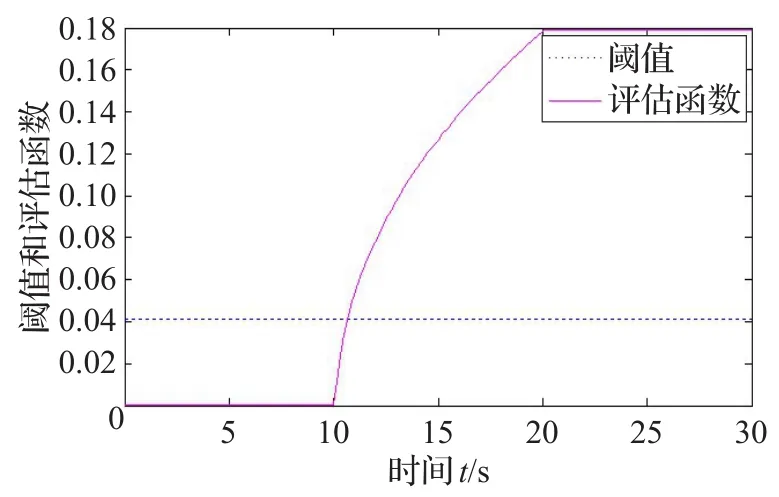
图4 τ0=0.01 s,τM=0.2 s时故障检测阈值与评估函数的响应

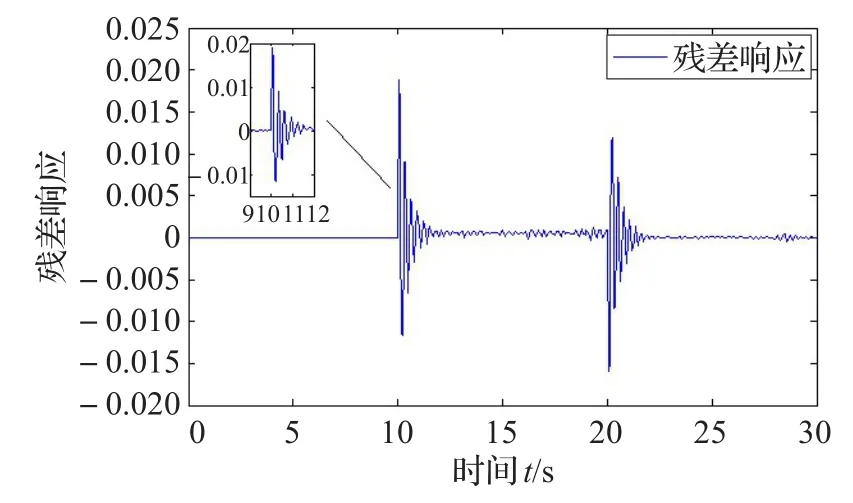
图5 τ0=0.01 s,τM=0.2 s时残差的响应

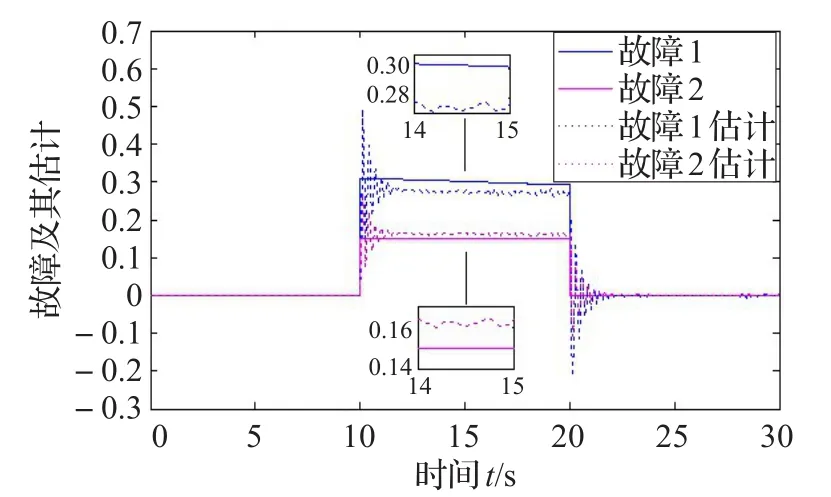
图6 τ0=0.01 s,τM=0.2 s时故障与故障估计的响应

当τM=2.5 s时，通过Matlab Toolbox求解定理1得到η=0.077 6。

此时ρ2=0.238 4。

图7描述的是当τ0=0.01 s,τM=2.5 s时，故障检测阈值与评估函数的响应。

图7 τ0=0.01 s,τM=2.5 s时故障检测阈值与评估函数的响应

图1和图4的阈值和评估函数的比较，证明了本文方法可以检测出故障，而图7是则显示出当时滞过大时，不能检测出故障。图2和图5描述的是故障发生时，在估计故障的过程中，残差信号的响应，并且可以看到时滞较大时，残差信号的超调量以及调节时间都会相应增大。图3和图6描述的是故障发生时，故障及其估计值的响应曲线，从中可以看出本文故障估计器可以较准确地估计出发生的故障，而随着时滞的增加，故障与其估计值之间的偏差会变大，故障估计的效果下降。

6 结论

本文针对包含时滞的随机分布系统，通过设计故障检测观测器和故障估计器，得到了故障检测与诊断的方法。通过仿真实验结果可以看出，本文提出的方法可以准确地对故障进行检测与估计。并且通过加入不同的时滞，得到时滞对故障检测与诊断的影响，可以看到故障估计的效果会随着时滞的增加而下降。

[1] Chen W T，Saif M.Fault detection and isolation based onnovelunknowninputobserverdesign[C]//Procof American Control Conference，2006：5129-5234.

[2] Karny M，Bohm J，Guy T V，et al.Mixture-based adaptive probabilistic control[J].Int J Adapt Control Signal Process，2003，17（2）：119-132.

[3] Gajic Z R，Losada R.Monotonicity of algebraic Lyapunov iterations for optimal control of jump parameter linear systems[C]//Proc ACC，1998：746-750.

[4] 张金芳.输出概率密度函数建模、控制及在分子量分布控制中的应用[D].北京：中国科学院，2005.

[5] Guo L.Self-convergence of weighted least-squares with applications to stochastic adaptive control[J].IEEE Trans on Automatic Control，1996，41（1）：79-89.

[6] Shalom Y B，Li X R，Kirubarajan T.Estimation with applicationstotrackingandnavigation[M].London：John Wiley and Sons，2001.

[7] Guo L，Wang H.PID controller design for output PDFs of stochastic systems using linear matrix inequalities[J].IEEE Trans on Syst，Man，Cybern B，2005，35（1）：65-71.

[8] Zhou J L，Yue H，Wang H.Shaping of output PDF based on the rational square-root B-spline model[J].Automatica，2005，31（3）：343-351.

[9] Zhang J F，Wang W，Zhang J H，et al.A rational squareroot B-spline model approximation output probability densityfunctionsfordynamicstochasticsystems[C]//Chinese Control and Decision Conference，2010：2609-2613.

[10] Zhang J F，Wang W，Zhang J H，et al.Probability density functionpredictivecontrolbasedontherational square-root B-spline model[C]//Chinese Control and Decision Conference，2009：4669-4672.

[11] Frank P M.Fault diagnosis in dynamic systems using analytical and knowledge-based redundancy：A survey and some new results[J].Automatica，1990，26（3）：459-744.

[12] Gertler J J.Fault detection and diagnosis in engineering systems[M].New York：Marcel-Dekker，1998.

[13] Chen J，Patton R.Robust model-based fault diagnosis for dynamic systems[M].Beijing：Kluwer Academic Publishers，1999.

[14] Liu J，Wang J L，Wang G H.Residual guaranteed variance filtering against sensor failures[J].IEEE Trans on Signal Processing，2003（5）：1403-1411.

[15] Wang H，Lin W.Applying observer based FDI techniques to detect faults in dynamic and bounded stochastic distributions[J].Int J Contr，2010，73：1424-1436.

[16] Zhang Y M，Guo L，Wang H.Filter-based fault detection and diagnosis using output PDFs for stochastic systems with time delays[J].Int J Adapt Control Signal Process，2006，20：175-194.

[17] Li T，Zheng W X，Yao X M.Fault detection and diagnosis using PDF for stochastic distribution systems[C]//Chinese Control Conference，2011：117-121.

[18] 桂卫华，杜建江，许辉灿，等.基于输出PDF的浮选故障检测和诊断方法[J].控制工程，2012，19（2）：307-310.

[19] 张显.时滞系统的故障诊断方法研究[D].山东青岛：中国海洋大学，2010.

[20] Moon Y S，Park P，Kwon W H，et al.Delay-dependent robust stabilization of uncertain state-delayed systems[J].International Journal of Control，2001，42（4）：1447-1455.

[21] Tian Y C，Yu Z G，Fridge C.Multifractal nature of network induced time delay in networked control systems[J].Physics Letters A，2007，361（1/2）：103-107.

[22] Chen W H，Zheng W X.Delay-dependent robust stabilization for uncertain neutral systems with distributed delays[J].Automatica，2007，43（1）：95-104.

[23] Wu M，He Y，She J H.New delay-dependent stability criteria and stabilizing method for neutral systems[J].IEEE Transactions on Automatic Control，2004，49（12）：2266-2271.

[24] He Y，Wu M.On delay-dependent robust stability for uncertain neutral systems[J].Journal of Systems Engineering and Electronics，2005，16（2）：351-355.

[25] Guo L，Wang H.Fault detection and diagnosis for general stochastic systems using b-spline expansions and nonlinear filter[J].IEEE Trans on Circuits and Systems I-REG，2005，52（8）：1644-1652.

[26] Seuret A，Gouaisbaut F.Wirtinger-based integral inequality：Application to time-delay systems[J].Automatica，2013，49（9）：2860-2866.

CHEN Long,LI Tao,XU Xiaofeng.Fault detection and diagnosis based on PDF and time-delay.Computer Engineering andApplications,2018,54（6）：257-263.

CHEN Long,LI Tao,XU Xiaofeng

School of Information and Control,Nanjing University of Information Science and Technology,Nanjing 210044,China

In this paper,a method of fault detection and diagnosis based on Probability Density Function（PDF）is proposed for stochastic distributed systems with time-delay.The residual of the PDF information is established firstly,then it designs fault detection observer and fault estimator based on the linear matrix inequality utilizing the theory of fault detection and diagnosis,and passes through the stability analysis,realizes fault detection and estimation of the system.Finally,the numerical simulation shows the effectiveness of the method.

time-delay;stochastic distribution system;fault detection and diagnosis;observer

针对包含时滞的随机分布系统，提出了一种基于概率密度函数（PDF）的时滞依赖故障检测与诊断方法。建立了基于PDF信息的故障检测残差，利用故障检测与诊断理论，设计了基于线性矩阵不等式的故障检测观测器和故障估计器，并且通过了稳定性分析，实现了对该系统的故障检测以及估计。通过数值仿真，证明了该方法的有效性。

时滞；随机分布系统；故障检测与诊断；观测器

2016-09-21

2017-01-17

1002-8331（2018）06-0257-07

A

TP271

10.3778/j.issn.1002-8331.1609-0295

国家自然科学基金（No.61573189，No.61573190）；江苏省杰出青年基金项目（No.BK20140045）；江苏省六大人才高峰计划（No.2015-DZXX-013）。

陈龙（1992—），男，硕士研究生，主要研究领域为故障检测与诊断，E-mail：1576163595@qq.com；李涛（1979—），男，博士，博士生导师，主要研究领域为时滞系统，故障诊断；徐啸峰（1992—），男，硕士研究生，主要研究领域为时滞系统。