地球同步轨道SAR快速BP成像算法

刘青，李景文

北京航空航天大学电子信息工程学院，北京100191

地球同步轨道SAR快速BP成像算法

刘青，李景文

北京航空航天大学电子信息工程学院，北京100191

CNKI网络出版：2017-05-10,http://kns.cnki.net/kcms/detail/11.2127.TP.20170510.1050.008.html

1 引言

合成孔径雷达（Synthetic Aperture Radar，SAR）的概念最早是由美国Goodyear航空公司的Carl Wiley于1951年首先提出的，它是测量地球表面特征的有效工具。较传统雷达相比，由于SAR成像不受云雾、光照等自然因素的影响，具有全天候、全天时成像能力，因此，SAR在国民经济和国防建设中得到了广泛的应用。自美国1978年成功发射世界上第一颗SAR卫星以来，各个国家相继成功发射了多颗SAR卫星。由于卫星观测不受国界和政治因素影响，SAR卫星已成为空间对地观测的新手段，使得空间对地观测跨上了新台阶。而GEO SAR具有重访周期短、对地观测范围大等特点，同时，由于GEO SAR轨道高度高不易摧毁，在军事上具有更广泛的应用前景，因此，研究GEO SAR意义重大。然而，由于受地球自转影响，在地球同步轨道上的卫星飞行轨迹近似为一个“8”字形，一般基于线性运动假设的算法比如RD、CS等算法将不再适合于同步轨道成像[1]，即使经过算法改进，一个周期内仍然有1/4时间无法成像。基于时域处理的后向投影（BP）算法，成像时不存在任何假设条件和理论近似，能够对任意飞行轨迹良好成像，适用于GEO SAR成像[2]，但是其逐点成像计算的过程，使得该算法运算量巨大。随着近年来计算机处理能力的大幅度提升以及对分辨率越来越高的要求，使得BP算法日益受到人们关注。另一方面，如何减少BP算法的运算量，成为学者研究的热点。近年来，研究人员先后提出了多种快速BP算法，主要包括有采用局部近似处理的局部后向投影[3-4]（LBP）和基于近似处理和孔径融合的快速因式分解后向投影[5-6]（Fast Factorized Back Projection，FFBP）等快速BP算法。这些快速算法的提出，不仅最大限度地保持了BP算法的高分辨率，同时大幅提高了BP算法的成像速度。其中LBP算法理论计算量由原来的N3下降到N5/2[7]，FFBP的理论计算量下降到N2lbN[8-9]。虽然后者要快于前者，但是前者实现起来比后者要简单，并且容易实现并行计算。目前，以上两种算法主要应用于机载超宽带SAR成像，由于累积误差影响，不能直接应用于GEO SAR成像。2010年，李财品提出一种在FFBP基础上改进的快速BP算法用于GEO SAR成像[10]，没有对累积误差进行必要说明，也没有给出具体成像质量评估指标。

本文通过分析LBP算法局部近似原理，提出了适用于GEO SAR的LBP成像处理方法。该方法能够有效解决传统LBP方法由于GEO SAR的超长合成孔径引起的误差积累而导致不能成像的问题。通过仿真数据验证了改进方法的有效性。

2 LBP算法原理

BP算法的成像过程是计算每个方位时刻雷达平台位置与成像区域每点的双程延时，然后在距离压缩的时域数据中取出每点对应的回波数据并加以补偿相位，再将不同方位时刻对应的投影数据进行相干累加，最后得出成像结果的过程[11]。

在正侧视条件下，假设经过距离向脉冲压缩后，点目标回波信号S(τ,t,R0)如下：

其中，B为距离向信号带宽，c为光速，λ为载频波长，τ、t分别为距离向时间与方位向时间，R0为波束中心照射点目标时的斜距，为点目标到达雷达的斜距，V为雷达平台等效速度。

根据BP算法的原理，将成像区域内的任意一点投影至回波域内，可以形成该点目标的徙动轨迹，将该徙动轨迹内的回波信号进行叠加，就能获得该点目标对应的复数据。如图1所示，则图像域内任意一点的复数据可以表示为：

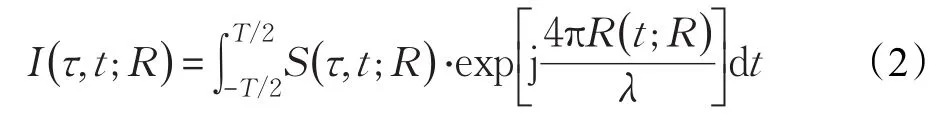
其中，T为方位向合成孔径时间。传统BP算法对于每个回波场景内每个像素点进行一次积累。

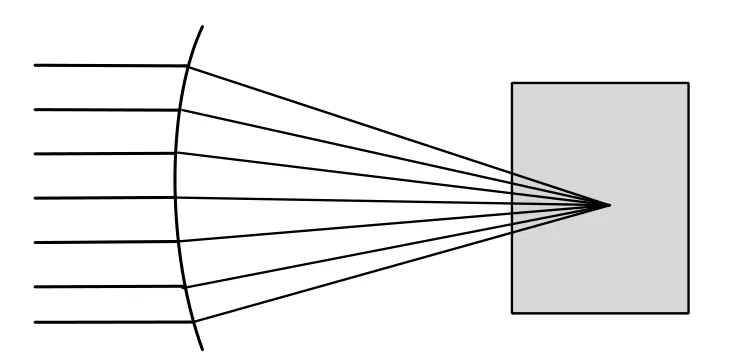
图1 后向投影示意图

2.1 局部近似原理

LBP算法之所以可以大幅减小BP的算法计算量，其根本原因就在于使用了局部近似处理[12]。在投影过程中，对于每个孔径，并不需要把回波数据投影到成像区域的所有像素点上去，如图2所示。每个孔径对应一组以孔径中心为圆心的同心圆，每个圆上的点的后向投影数据是相同的。对于某个孔径t，两边相邻的孔径在图中所示的扇形波束内，可以近似认为它们具有相同的同心圆，即相同的回波数据。而扇形区域内的回波数据与孔径中心和区域中点的连线即中心线上的回波数据是一致的，因此在一定的距离误差允许范围内，可以用一条中心线代替该扇形区域。在直角坐标系下，图中矩形区域内的投影数据可以用图中中心线（粗虚线）代替。区域内的其他位置的投影数据由这条中心线插值得到。图2中，P点的投影数据用P′点代替，P和P′位于以孔径中心t为圆心，tP′为半径的圆弧上。LBP算法把原本对一个区域做的后向投影变成对区域内的一条中心线做后向投影，从而减少了算法的计算量。

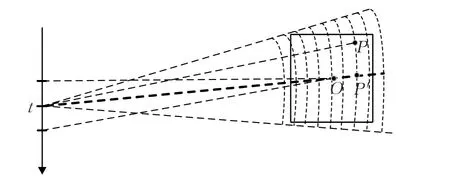
图2 局部近似示意图

引入了近似处理，必然会带来误差，进而影响成像质量。如图3所示，根据近似原理，中心线附近的点使用中心线上的点代替。中心线一般选择孔径中心到区域中心的连线，并且截取覆盖子区域的一段。由于子区域中所有像素点都需要用中心线上的点代替，为保证截取的线段能覆盖所有点，截取的中心线的长度要选择适当。如果过短，将无法保证子区域每个点都能覆盖，过长则冗余数据过多。如图3中，中心线上的线段ab是最理想的长度。每个子孔径对应的中心线都不一样，因此，实际处理中应选择比ab要长一些的线段。中心线上的投影数据是通过传统BP算法投影计算得出的，是没有误差的，而不在中心线上的点P，则由P′点近似，即认为孔径O和孔径t在P′点的投影数据相同。P点和P′点位于以孔径t为圆心，半径为r的同一个圆弧上。

图3 距离误差示意图

由于BP算法是根据孔径中心到成像区域每个像素点的斜距，然后在距离压缩数据中寻找对应的回波数据，因而对于孔径O，用P′点近似P点，会因为斜距OP和OP′的不同引入误差。两者的斜距差决定误差大小ΔR。

根据图中几何关系可以得出距离差表达式为：

一般假设斜距差||ΔR≪R，于是距离误差可以近似表达为：

根据文献[2]，可以得出距离误差的进一步表达式：

其中D为垂直于区域中心线的宽度，d为子孔径长度，从上式可以看出，只要保持成像子区域宽度和子孔径长度的乘积不变，就可以控制误差大小，因此，只要在处理过程中保证距离误差在允许范围内，相邻孔径就可以作近似处理。

2.2 成像区域和子孔径划分

成像区域的划分对算法计算量和成像质量影响较大[13]。成像时，每个子孔径中心需要对每个子区域中心线进行投影计算。由此可见，中心线的总长度将会影响算法的计算量，减少中心线的总长度将会进一步降低计算量，而中心线总长度与成像区域划分密切相关，子区域划分的越多，中心线总长度就长，计算量相应会增大；相反，子区域少，计算量则减少。因此，最佳的划分方法应该是在保证在一定误差情况下，使得成像区域分块最少。另一方面，在由中心线数据投影到子区域的过程中，需要计算孔径中心到子区域每个像素点的双程延时，从而产生大量的计算，因此，子孔径数量的多少也是影响算法计算量的重要因素。所以，应该在保证误差的情况下，将更多的孔径近似处理，合并为一个子孔径。GEO SAR合成孔径长，这也带来一个数据存储量巨大的问题。文献[14]提出可以将全孔径分为若干个孔径块分别进行处理。在每个孔径块的基础上再划分子孔径成像，分别对每个孔径块成像，最后将所有孔径块成像结果进行相干叠加得到最终成像结果，这样可以避免计算时数据量过大从而导致内存不足的问题。当计算机内存配置不足时可以采用该方法。

导出最大距离误差表达式：

为了更好地控制误差大小，一般将最大距离误差表示为：

其中M为误差控制因子，通常不小于16，λ为工作波长。结合式（6）和（9）可以得出子区域方位向宽度表达式：

考虑到子区域的选择要满足一个合成孔径角内所有子孔径，因此，所选子区域应该包含于所有扇形交集内的区域。如图4所示。LBP算法在区域划分时，通过式（10），根据成像区域分块数和子孔径数最少的原则，确定方位向宽度，将成像区域方位向等间隔划分，距离向以同样的数量等间隔划分，同时选择合适的子孔径长度。

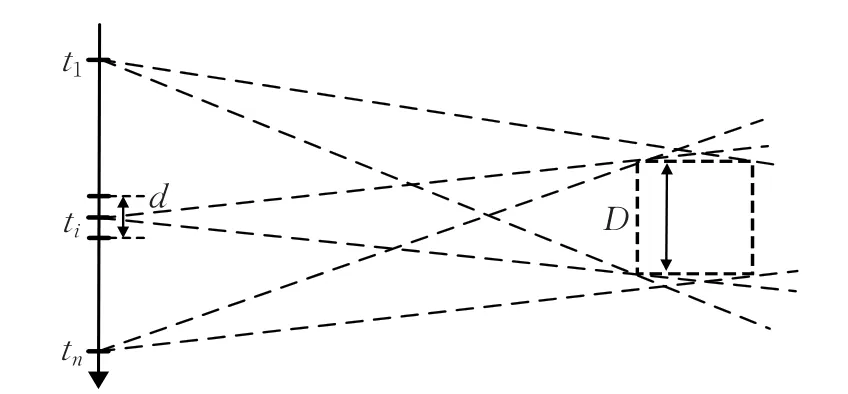
图4 成像区域划分示意图

3 误差分析

LBP算法主要包含两大步骤，第一是将子孔径数据投影到子区域中心线上，期间需要根据孔径到投影点的双程延时进行一次相位补偿。第二步是将中心线数据投影到子区域其他位置。考虑到数据存储问题，中心线上的数据只是若干离散点的数据，因此，为减少误差，在投影前需要先将中心线数据插值处理，并且还需以同样的插值倍数将中心线投影点的位置插值出来。如图5所示，将中心线上某处相邻的a、b两点做8倍插值处理，两点之间均匀插入7个点。中心线上的数据在作插值处理后，每个插值点都有对应的投影数据。投影过程中，以子孔径中心O为圆心，OP为半径画圆，圆弧与中心线相交的点是理论上的投影点。虽然已作插值，但实际上，P点仍然会以极大概率不会正好投影到插值的点上，而是会投影在中间的某个位置P′。在取投影数据时，由于P′点处没有投影数据，则是用距离P′点最近的插值点P″的投影数据代替，因而会带来大小为dr的斜距误差。传统LBP算法在成像时没有考虑该项误差。

图5 插值示意图

理论上，这个斜距误差是可以通过提高插值倍数来降低的，插值倍数越高，误差越小。但是该误差会随着子孔径叠加而累积，子孔径越多，累积误差将越大，从而可能会影响到成像质量。

4 数据仿真

为了分析子孔径叠加对成像质量的影响，下面利用传统LBP算法应用于GEO SAR点目标成像仿真。仿真实验的计算机处理器为Intel®Xeon®E5-2650，主频2.30 GHz，内存256 GB，运行环境为MATLAB R2015a，系统仿真参数见表1，成像结果如图6所示。

表1 系统仿真相关参数

图6 点目标聚焦结果

图6分别给出了32、64倍插值的成像结果，图7给出了每个子孔径内的最大距离误差。针对第3章中的距离误差对成像的影响，利用式（8）以及仿真参数可以得出允许的最大斜距误差为0.015 m。理论上，将插值倍数提高后，距离误差将降低。从图中可以看出，当采用32倍插值后，子孔径最大距离误差已经低于允许值，但是从成像结果来看，聚焦效果仍然不是很理想，即使插值倍数提高到64倍，子孔径最大距离误差再次降低的情况下，成像结果与传统BP结果仍有差距。

图7 子孔径最大距离误差

图8显示了64倍插值后，子孔径叠加之后每个像素点的距离误差，平均误差为0.024 4 m，大于0.015 m。从上述结果可以看出，成像质量差的原因是由GEO SAR的长合成孔径所导致的。对于单个子孔径来说，这个距离误差影响很小，但是由于GEO SAR全孔径长，即使划分为子孔径，子孔径数仍有数百个之多，将所有子孔径成像结果相干叠加之后，即使微小的距离误差也会被放大数百倍，从而导致成像质量下降。只有将插值倍数提高到与子孔径数相近的倍数，才可能消除由子孔径叠加带来的影响，但是这也使得计算量以及内存使用量显著增大，为了进一步验证上述结论，将LBP算法用于较短孔径的机载SAR成像。图9给出了LBP算法和BP算法成像对比。系统合成孔径长度（点数）为768，子孔径数48。从结果可以看出，采用48倍插值之后，两种算法结果基本一致。

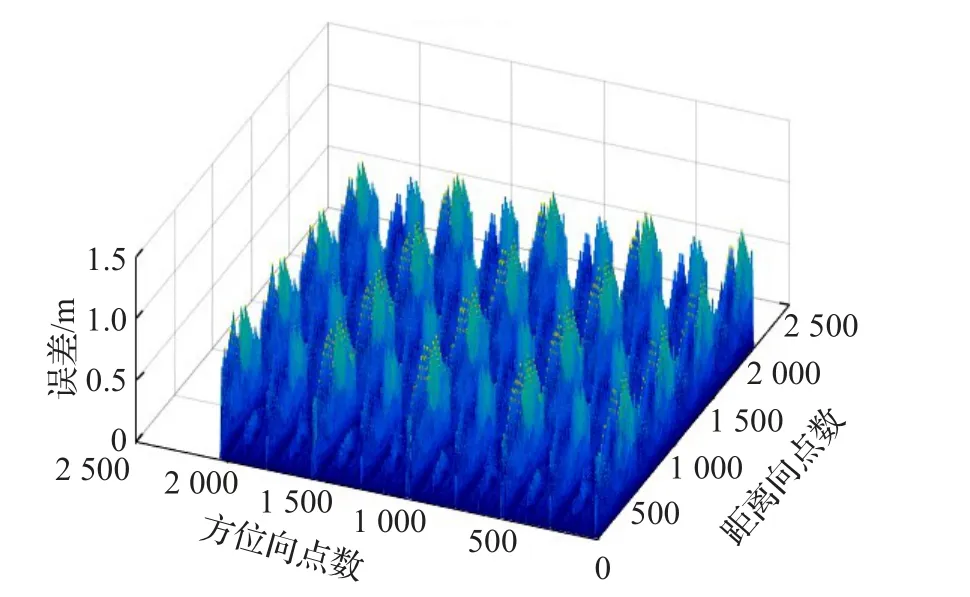
图8 误差分布

因此，对于长孔径的GEO SAR来说，通过提高插值倍数来减少误差的做法并不适用，必须在叠加前予以相位补偿，即在每个像素点的复数据后乘以一个补偿相位，补偿相位大小为：

图10给出了相位补偿前后成像结果对比图，采用8倍插值。在相位补偿前，点目标聚焦效果很差，补偿后则能够很好地聚焦。通过对比可以很明显地看出相位补偿的必要性。

图11分别给出了两种算法点目标仿真成像结果，成像质量评估参数如表2所示。从表2中可以看出，使用改进LBP算法和传统BP算法得到的图像质量基本相近，改进LBP算法的方位向分辨率比BP算法仅降低了1.5 cm，相对于米级的分辨率可以忽略，距离向分辨率保持不变。峰值旁瓣比与积分旁瓣比均只有微小变化，但是改进LBP算法的成像时间却只是传统BP算法的1/75。传统算法需要3.7 h才能完成成像，而快速算法只需要3 min就可以完成，加速效果很明显。

表2 点目标成像质量对比

图9 机载合成孔径成像结果

图10 相位补偿前后对比

图11 点目标成像结果

5 算法实现步骤

经过上述分析，在LBP算法基础上得到一种改进的LBP算法，算法实现步骤总结如下：

（1）选择合适的子孔径长度和数量划分孔径，L=d×n，其中L表示全孔径长度，d为子孔径长度，n为子孔径个数。

（2）通过式（10）选择合适的子区域划分，确定子区域中心线，并对中心距离线进行离散采样，确定投影点。

（3）将子孔径内每个小孔径的距离压缩数据按照传统BP算法投影到每个子区域中心线上。

（4）将子区域中心线数据投影到子区域每个像素点，并进行相位补偿，然后将成像区域的所有子区域数据拼接，得到子孔径图像。

（5）将得到的所有子孔径图像相干叠加，得到最终图像。

6 算法性能分析

由改进LBP算法的处理过程可知，其计算量与其子孔径及子区域划分相关。为了分析方便，假定原始数据方位向、距离向和成像区域的方位向、距离向点数均为N，则传统BP算法的计算量为N3。采用改进LBP算法，全孔径分成个子孔径，每个子孔径包含的孔径数为，成像区域同样分成块。第一步由子孔径投影到中心线，每个子孔径中的每个小孔径需要对个像素点投影，一共有个孔径，则第一步的计算量为第二步由中心线投影到子区域，每个子孔径中心需要对N×N个像素点投影，一共有个子孔径，则第二步的计算量为算法总的计算量为由此可知，改进LBP算法可以大幅度降低计算量，当N越大时，加速效果更明显。

实际上，上述计算量分析并不能定量地描述算法的加速效率。由于在进行投影操作时需要进行插值计算，并且需要计算斜距误差并进行第二次相位补偿，等等，这些都将影响算法的计算量。不同的插值方法带来的成像质量和计算量也略有不同。常用的插值方法包括有频域插值、最近邻域插值、三次样条插值、线性插值等。文献[15]研究了几种常用插值方法对快速BP成像质量和算法效率的影响。

7 结束语

针对传统LBP算法不能用于GEO SAR成像的问题，在LBP算法的基础上，在每个子孔径叠加之前进行一次相位补偿，得到一种适用于GEO SAR成像的改进LBP算法，并给出了算法实现的步骤。仿真结果表明改进算法基本保持了传统BP算法的成像质量，同时大幅降低了算法的计算量。

[1] Li C，He M.Signal characteristics analysis of GEO SAR[C]//IET International Radar Conference，2013：1-5.

[2] 李春升，杨威，王鹏波.星载SAR成像处理算法综述[J].雷达学报，2013，2（1）：111-122.

[3] Yegulalp A F.Fast backprojection algorithm for synthetic aperture radar[C]//1999 Radar Conference，1999：60-65.

[4] Ahmed I.Study of the local backprojection algorithm for image formation in ultra wideband synthetic aperture radar[D].Sweden：Bleking Institute of Technology，2008.

[5] Yu Hongtao，Zhang Y S，Zhu L L.UWB LFMCW radar imaging based on dechirp processing[J].Modern Radar，2005.

[6] 刘光平.超宽带合成孔径雷达高效成像算法[D].北京：中国人民解放军国防科学技术大学，2003.

[7] Shao Y，Wang R，Deng Y，et al.An N2.5 back-projection algorithm for SAR imaging[C]//Geoscience and Remote Sensing Symposium，2012：2113-2116.

[8] Mccorkle J W，Rofheart M.Order N^2log（N）back projector algorithm for focusing wide-angle wide-bandwidth arbitrary-motion synthetic aperture radar[J].Proceedings of SPIE：Radar Sensor Technology，1996，2747：25-36.

[9] Basu S，Bresler Y.O（N2log2N）filtered back projection reconstruction algorithm for tomography[J].IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society，2000，9（10）：1760-1773.

[10] 李财品，张洪太，谭小敏.一种适合GEOSAR成像改进的快速BP算法[J].现代防御技术，2010，38（5）：77-81.

[11] Li Z，Li C，Yu Z，et al.Back projection algorithm for high resolution GEO-SAR image formation[C]//IEEE International Geoscience and Remote Sensing Symposium，Vancouver，BC，Canada，2011：336-339.

[12] 刘光平，梁甸农.适用大场景高分辨合成孔径雷达的快速BP算法[J].系统工程与电子技术，2003，25（5）：546-549.

[13] 林世斌，李悦丽，严少石，等.基于最优区域划分的子块快速因子分解后向投影算法[J].信号处理，2012，28（8）：1187-1193.

[14] Ulander L M H，Hellsten H，Stenstrom G.Synthetic aperture radar processing using fast factorized backprojection[J].IEEE Transactions on Aerospace and Electronic Systems，2003，39（3）：760-775.

[15] Frolind P O，Ulander L M H.Evaluation of angular interpolation kernels in fast back-projection SAR processing[J].IEEE Proceedings：Radar Sonar and Navigation，2006，153（3）：243-249.

LIU Qing,LI Jingwen.Fast back projection algorithm for GEO SAR.Computer Engineering and Applications,2018,54（6）：241-246.

LIU Qing,LI Jingwen

School of Electronics and Information Engineering,Beihang University,Beijing 100191,China

The back projection algorithm using local approximation（LBP,Local Back Projection）is not suitable for imaging in Geosynchronous SyntheticAperture Radar（GEO SAR）for the sake of high orbit and extremely long synthetic aperture.Combined with the traditional LBP algorithm principle,the GEO SAR phase error model based on LBP is constructed,and the LBP imaging processing method suitable for GEO SAR is proposed.The imaging results have the same quality with traditional BP algorithm,the computational efficiency is increased by 75 times.

Geosynchronous SyntheticAperture Radar（GEO SAR）;Local Back Projection（LBP）;phase compensation

地球同步轨道合成孔径雷达（Geosynchronous Synthetic Aperture Radar，GEO SAR）轨道高，合成孔径长，采用局部近似处理的后向投影算法（Local Back Projection，LBP）不再适用。结合传统LBP算法原理，构建了基于LBP的GEO SAR相位误差模型，提出了适用于GEO SAR的LBP成像处理方法。仿真结果表明改进后的LBP算法在保证成像质量与传统BP算法基本相近的同时，将计算效率提升了75倍。

地球同步轨道合成孔径雷达；局部后向投影；相位补偿

2016-10-19

2017-01-12

1002-8331（2018）06-0241-06

A

TN957.52

10.3778/j.issn.1002-8331.1610-0216

刘青（1985—），男，硕士研究生，主要研究领域为地球同步轨道SAR成像，E-mail：sy1402424@buaa.edu.cn；李景文（1964—），男，博士，教授，主要研究领域为合成孔径雷达运动目标监测与成像、新体制微波遥感理论与方法等。