基于熵和改进的协相关度的直觉模糊决策方法

王斌，王哲辰，周炜，郝天鹏

1.青岛理工大学，山东青岛266033

2.北京航空航天大学，北京100191

基于熵和改进的协相关度的直觉模糊决策方法

王斌1，王哲辰2，周炜1，郝天鹏1

1.青岛理工大学，山东青岛266033

2.北京航空航天大学，北京100191

CNKI网络出版：2017-04-14,http://kns.cnki.net/kcms/detail/11.2127.TP.20170414.1723.022.html

1 引言

Zadeh于1965年提出的模糊集理论[1]，利用隶属度函数来刻画客观世界的模糊性，奠定了模糊数学的基础。1986年Atanassov提出了直觉模糊集[2-3]（Intuitionistic Fuzzy Set，IFS）的理论，通过引入非隶属度函数和犹豫度等概念，能够更加深入、细致地分析事物的模糊性，是对模糊集理论最有影响的一种扩充和发展，关于直觉模糊集问题的研究近年来引起了人们的广泛关注，并在决策分析、知识发现等领域已得到了广泛应用[4-8]。

为了刻画直觉模糊集的模糊程度，Burillo等在1996年最先给出直觉模糊熵的定义[9]，Szmidt等于2001年又给出另一种直觉模糊熵的定义[10]。此后，有关直觉模糊熵的研究吸引了许多学者的关注，如文献[11-12]在上述两种定义的基础上，提出了改进的直觉模糊集合熵的公理化定义和一般构造形式；文献[13]构造了一类指数直觉模糊熵；文献[14]构造了二个三角函数直觉模糊熵；文献[15-16]在熵的构造中加入了犹豫度函数，分别利用余弦函数、余切函数构造了直觉模糊熵，克服了当隶属度与非隶属度的绝对偏差相同的任意两个直觉模糊集，其直觉模糊熵值相同这一缺陷。文献[17]又进一步研究了区间直觉模糊熵的问题。两个直觉模糊集之间相关系数的概念在文献[18]中被提出，但没有考虑决策者的风险态度及不同属性的权重及对相关系数的影响；为了克服文献[18]中相关系数处理的不足，文献[19]根据文献[20]中关于相关系数的定义结构，考虑了决策者的态度，引入了态度参数，提出了两个直觉模糊集协相关度的概念，并以此为基础，提出一种多属性决策方法。

本文在文献[19]的基础上，改进了两个直觉模糊集协相关度的公式，提出了两个直觉模糊集的相关系数，克服了文献[19]中协相关度的定义的不足，改进了决策者的风险态度参数，并给出了一种新的广义直觉模糊熵，推广了文献[11-12，19]中直觉模糊熵的公式，使其成为本文直觉模糊熵的三种特例。然后借鉴文献[21]的方法，利用熵的最小化原则建立优化模型确定属性权重，计算各对象与理想对象之间的相关系数，从而得出一种有效的多属性决策方法，最后通过实例进行了验证。

2 预备知识

下面首先给出直觉模糊集的一些基本概念。

定义1[2]设U是一个给定的论域，称三元组A=为U上的直觉模糊集，记为IFS。其中：uA,vA皆是U→[0,1]上的映射，且0≤uA(x)+vA(x)≤1，uA(x),vA(x)分别表示元素x属于直觉模糊集A的隶属度和非隶属度。令πA(x)=1-uA(x)-vA(x)，称为x属于直觉模糊集A的犹豫度，显然0≤πA(x)≤1，以下简记U上的所有直觉模糊集的全体，记为IFS(U)，U上的全体经典集合记为P(U)。

定义2[2]设，则运算法则如下：

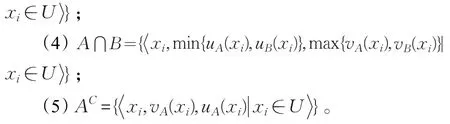
直觉模糊集中的隶属度、非隶属度及犹豫度这三个重要参数，对直觉模糊集的形成具有决定意义，它们从不同的侧面反映了论域中元素的不确定性，为了度量直觉模糊集的这种不确定性，一些学者提出了直觉模糊熵的概念，用以刻画直觉模糊集所包含的不确定性。下面首先给出直觉模糊熵的公理化定义。

定义3[22]如果实值函数E:IFS(U)→[0,1]满足下面条件，则该实值函数称为直觉模糊熵。

（1）E(A)=0，当且仅当A是一个分明集；

（2）E(A)=1，当且仅当∀xi∈U,πA(xi)=1；

（3）E(A)=E(AC)；

（4）E(A)=f(ΔA,πA)是一个连续函数且关于参数ΔA是递减的，关于参数πA是递增的。

在文献[11-12，19]的基础上，给出了一种改进的广义直觉模糊熵。

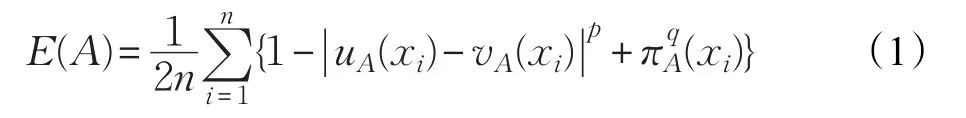
定理1设，则是直觉模糊集A的熵，其中p＞0，q＞0。

证明（1）若A是一个分明集，则uA=1,vA=0或uA=0,vA=1,所以且πA=0,故E(A)=0。

∀xi∈U,因，故，若E(A)=0，则，因为0≤，所以，即uA=1,vA=0或uA=0,vA=1，A是一个分明集。

（2）若∀xi∈U,πA(xi)=1，则uA(xi)=0,vA(xi)=0，

（4）为了证明式（1）满足定义3中的条件（4），只需证明函数f(x,y)=1-xp+yq关于x递减，关于y递增即可，其中p＞0,q＞0,x,y∈[0,1]。求导得=-pxp-1＜0,=qyq-1＞0,所以f(x,y)关于x递减，关于y递增。证毕。

比较文献[11-12，19]和本文式（1）给出的直觉模糊熵定义，当式（1）中p=q=1时即得文献[11]给出的直觉模糊熵E1(A)；当式（1）中p=q=2时即得文献[12]给出的直觉模糊熵E2(A)；当式（1）中p=2,q=1时即得文献[19]给出的直觉模糊熵E3(A)；因此，本文给出的是一种改进的更具一般性的直觉模糊熵。

3 直觉模糊熵属性权重与理想对象的确定

在多属性决策中，一般通过属性权重来刻画不同属性的不同重要性。以往凭经验给出权重的方法常常带有主观性，往往不能客观地反映实际情况，造成决策失误。本文仍然采用文献[21]中客观的非线性规划方法来确定权重。

假设对象集U={x1,x2,…,xn}，属性集A={a1,a2,…,am},属性权重向量wj∈[0,1]。

在实际决策中，为了提高决策的准确性和科学性，决策者往往希望决策问题的确定性信息越多越好，而不确定性信息越少越好，因此各属性的权重安排应尽量减少不确定信息对决策的影响，即权重的安排应使所有属性的总熵值最小，故可建立如下的优化模型。

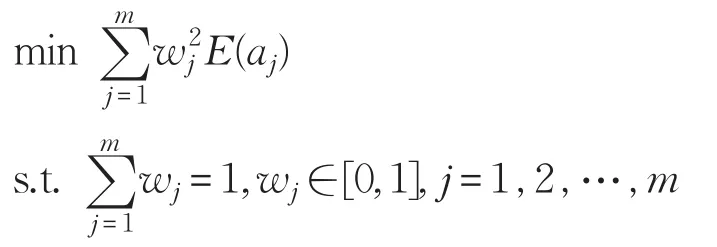
对上述模型，使用Lagrange乘数法可解得：

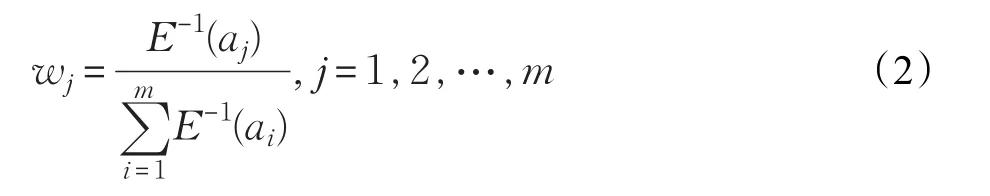
由式（2）可以看出，当某个属性所包含的不确定信息越少，即直觉模糊熵越小，其相应的权重就越大，对总体决策的影响也就越大，符合前述对权重确定的要求。

在多属性决策中，为了对不同对象进行比较，从而确定最优策略，借鉴逼近理想解排序（Technique for Order Preference by Similarity to all Ideal Solution，TOPSIS）方法的思想，从每个属性中选择最好的属性值组成一个理想对象，然后把各个对象与理想对象一一作比较。即求出它们的相关系数，实现对对象进行排序，从而得出最优策略。在直觉模糊信息环境下各属性的理想对象x*的理想值可按如下方法选取：

其中uj(x*),vj(x*),πj(x*),分别表示理想对象x*在第j(j=1,2,…,m)个属性下的隶属度、非隶属度和犹豫度。

4 直觉模糊集的相关系数

文献[19]给出的协相关度的定义为：

此定义的思路借鉴自概率论中协方差的定义，cov(X,Y)=E{[X-E(X)][Y-E(Y)]}。因为u(xi)+v(xi)+π(xi)=1，即这相当于将任一隶属度函数的期望值u(xi)都取值为1/3，显然与协方差定义中E(X)的意义不符，此定义是需要改进的。因此，给出协相关度的一种新的定义，称之为直觉模糊集的相关系数。

定义4设论域U={x1,x2,…,xn}，属性集α={a1,a2,…,am},w={w1,w2,…,wm}为属性权重向量，wj∈[0,1],A={xi,uj(xi),vj(xi)|xi∈U}∈IFS(U)，其中uj(xi),vj(xi)分别为对象xi在属性aj时的隶属度和非隶属度。

则式（1）隶属度相关系数为：

表1 候选人评价结果

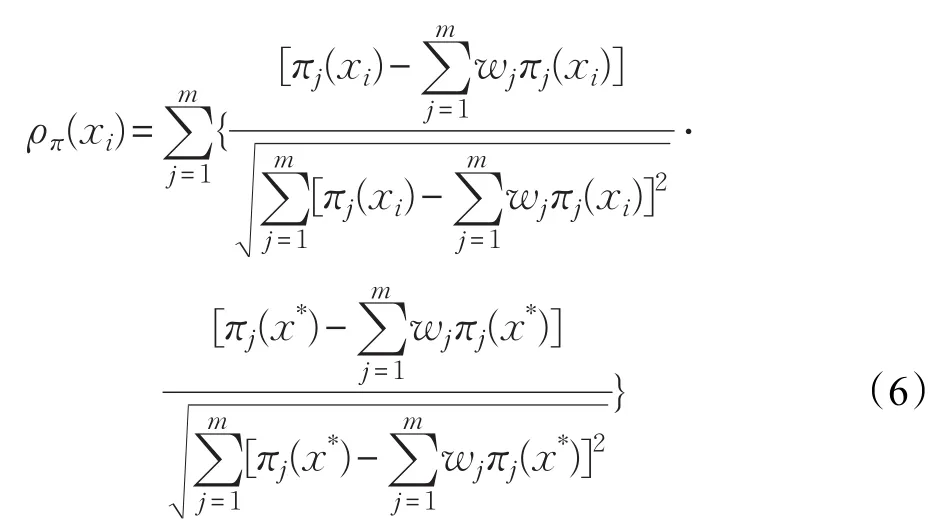
定义5（得分函数）设ρu(x),ρv(x),ρπ(x)分别为对象x的隶属度相关系数，非隶属度相关系数和犹豫度相关系数，则得分函数为：

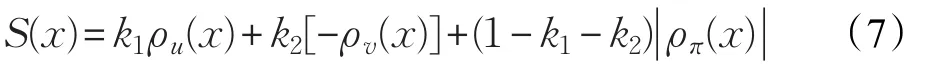
其中常数ki表示决策者的决策态度，0＜k1,k2＜1,k1+k2＜1,若表示决策者是悲观型的；若＜k1,k2＜1,表示决策者是乐观型的；若k1=k2=,表示决策者是中立型的。

定理2得分函数S(x)∈[-1,1]。

证明因为ρu(x),ρv(x),ρπ(x)均为相关系数，故其绝对值不大于1，即||ρ*(x)≤1，所以

在具体决策中，得分函数值S(x)越大，说明对象x越靠近理想解x*，对象x就越优。于是，得到一种基于熵和改进的协相关度的直觉模糊环境下的多属性决策方法，具体步骤如下：

（1）利用式（1）计算各个属性的直觉模糊熵E(ai)，(i=1,2,…,n)；利用式（2）求出属性的权重wj(j=1,2,…,m)。

（2）利用式（3）确定理想对象x*。

（3）分别利用式（4）～（6）计算各个属性对象的隶属度相关系数，非隶属度相关系数和犹豫度相关系数。

（4）根据决策者的决策态度选择适当的ki值，利用式（7）计算各个对象得分函数S(xi)的值。

（5）根据每个对象的得分函数S(xi)的值，对各个对象进行排序，从而得到最优对象。

5 实例分析

例1[19]某高校老师准备评选教授，只有一个名额，共有8名候选人U={x1,x2,…,x8}符合晋升条件。为了确定最佳候选人，该校评审组对这8名候选人分别从6个方面A={a1,a2,…,a6}（假设这6个方面均是效益型指标）进行评价，并将评价结果以直觉模糊信息的形式给出，如表1所示。

下面使用本文方法确定最佳候选人。

（1）利用式（1）计算各个属性的直觉模糊熵，得E(a1)=0.476 2,E(a2)=0.562 5,E(a3)=0.564 4,E(a4)=0.553 1,E(a5)=0.573 8,E(a6)=0.660 6,利用式（2）求出属性的权重w={0.196,0.165 9,0.165 4,0.168 7,0.162 7,0.141 3}。

（2）利用式（3）确定理想对象x*={＜0.8,0.1＞,＜0.7,0.2＞,＜0.6,0.2＞,＜0.8,0.1＞,＜0.6,0.2＞,＜0.5,0.2＞}。

（3）分别利用式（4）～（6）计算各个属性对象的隶属度相关系数，非隶属度相关系数和犹豫度相关系数。

（4）假设决策者是乐观型的，取k1=0.45,k2=0.35,利用式（7）计算各个对象得分函数S(xi)的值S(x)={0.354 5,0.058 6,-0.037 5,0.401 6,0.237 7,0.114,-0.365 3,-0.014 5}。

（5）根据每个对象的得分函数S(xi)的值，得到x4＞x1＞x5＞x6＞x2＞x8＞x3＞x7，从而得到最佳候选人为x4。

若决策者是悲观型的，取k1=0.25,k2=0.2，同理可得x4＞x1＞x5＞x6＞x8＞x3＞x2＞x7；若决策者是中立型的，取k1=k2=，得到x4＞x1＞x5＞x6＞x2＞x8＞x3＞x7。比较三种不同结果发现，对象x2,x3,x8之间的排序发生了变化，说明不同的决策态度对排序结果会产生一定影响，但最佳与最差对象仍然是x4,x7。

6 结束语

本文综合考虑直觉模糊集的直觉性和模糊性对不确定信息的影响，在原有文献的基础上，给出了一种改进的直觉模糊熵，概括并推广了原有的一类直觉模糊熵的定义。针对原有文献提出的两个直觉模糊集协相关度概念存在的问题，改进了直觉模糊集协相关度的定义，构造了新的得分函数，由此给出了一种改进的基于直觉模糊信息的多属性决策方法，最后通过实例计算验证了该方法的有效性和可行性。

本文主要探讨用相关系数处理存在线性关系的直觉模糊集之间的相关问题，如果序列存在非线性相关性，到目前为止，还没有人能够给出类似于相关系数那样的为大家普遍认可的描述非线性关系的表达式。目前初步考虑二种处理方法：一是通过适当的变量变换将非线性关系转化为线性关系；二是如果不能够转化，需进一步研究探讨直接处理非线性相关性的方法。当然，这样的问题更加复杂，也是下一步将要深入研究的问题。

[1] Zadeh L A.Fuzzy sets[J].Information Control，1965，8（3）：338-353.

[2] Atanassov K.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems，1992，20（1）：87-96.

[3] Atanassov K.More on intuitionistic fuzzy sets[J].Fuzzy Sets and Systems，1989，33（1）：37-45.

[4] Li D F.A ratio ranking of triangular fuzzy number and its application to MADM problems[J].Computers and Mathematics with Applications，2010，60（6）：1557-1570.

[5] Wan S P.Multi—attribute decision making method based on possibility variance coefficient of triangular intuitionistic fuzzy numbers[J].International Journal of Uncertainty，Fuzziness and Knowledge—Based Systems，2013，21（2）：223-243.

[6] Wang J Q，Zhang Z.Aggregation operators on intuitionistic trapezoidal fuzzy number and its application to multi—criteria decision making problems[J].Journal of Systems Engineering and Electronices，2006，20（2）：321-326.

[7] 万树平.直觉模糊多属性决策方法综述[J].控制与决策，2010，25（11）：1601-1606.

[8] Wan S P.Power average operators of trapezoidal intuitionistic fuzzy numbers and application to multi—attribute groupdecisionmaking[J].Appliedmathematicalmodelling，2013，37（6）：4112-4126.

[9] Burillo P，Bustince H.Entropy on intuitionistic fuzzy sets and on interval—valued fuzzy sets[J].Fuzzy Sets and Systems，1996，78（3）：305-316.

[10] Szmidt E，Kacprzyk J.Entropy for intuitionistic fuzzy sets[J].Fuzzy Sets and Systems，2001，118（3）：467-477.

[11] 吴涛，白礼虎，刘二宝，等.直觉模糊集新的熵公式及应用[J].计算机工程与应用，2013，49（23）：48-51.

[12] Gao M，Sun T，Zhu J.Revised axiomatic definition and structural formula of intuitionistic fuzzy entropy[J].Control and Decision，2014，29（3）：470-474.

[13] Verma R，Sharma B D.Exponential entropy on intuitionistic fuzzy sets[J].Kybernetika，2013，49（1）：114-127.

[14] Ye J.Two effective measures of intuitionistic fuzzy entropy[J].Computing，2010，87（1/2）：55-62.

[15] 王坚强，王佩.基于直觉模糊熵的直觉语言多准则决策方法[J].控制与决策，2012，27（11）：1694-1698.

[16] Wei C，Gao Z，Guo T.An intuitionistic fuzzy entropy measure based on trigonometric function[J].Control and Decision，2012，27（4）：571-574.

[17] Nguyen H.A new interval-valued knowledge measure for interval-valued intuitionistic fuzzy sets and application in decision making[J].Expert Systems With Applications，2016，56：143-155.

[18] Park D G，Kwun Y C，Pa R K J H，et al.Correlation coeff icient of interval-valued intuitionistic fuzzy sets and its application to multiple attribute group decision maki ng problems[J].Mathematical and Computer Modelling，2009，50（9/10）：1279-1293.

[19] 汪峰，毛军军，黄超.基于熵和协相关度的直觉模糊多属性决策方法[J].计算机应用，2015，35（12）：3456-3460.

[20] Shen H.Probability theory and mathematical statistics[M].Beijing：Higher Education Press，2011：151-154.

[21] Wu J，Zhang Q.Multicriteria decision making method based on intuitionistic fuzzy weighted entropy[J].Expet Systems with Applications，2011，38（1）：916-922.

[22] Mao J，Yao D，Wang C.A novel cross-entropy measures of IFSs and their applications[J].Knowledge-Based Systems，2013，48（2）：37-45.

WANG Bin,WANG Zhechen,ZHOU Wei,et al.Intuitionistic fuzzy decision-making method based on entropy and improved co-correlation degree.Computer Engineering andApplications,2018,54（6）：247-251.

WANG Bin1,WANG Zhechen2,ZHOU Wei1,HAO Tianpeng1

1.Qingdao Technological University,Qingdao,Shandong 266033,China
2.Beihang University,Beijing 100191,China

Aiming at the multi-attribute decision-making problems with unknown attribute weight and Intuitionistic Fuzzy Set（IFS）as decision information,and the problems in researching decision-making methods on the basis of co-correlation degree,a decision-making method based on Intuitionistic Fuzzy（IF）entropy and modified co-correlation degree is proposed.In precise measurement of the intuitionism and fuzziness of IFS,a formula of improved IF entropy,which generalizes and extends the original formula of IF entropy,has been presented and adequately discussed.Moreover,from the structure of the correlation coefficient in probability statistics,the definition of co-correlation degree of IFS is improved by structuring the correlation coefficient and score function between IFS and ideal objects.Thus,an improved multi-attribute decision-making method based on intuitionistic fuzzy information is given,experimental results prove the effectiveness and feasibility.

intuitionistic fuzzy set;intuitionistic fuzzy entropy;co-correlation degree;score function

针对决策信息为直觉模糊集且属性权重未知的多属性决策问题，以及关于协相关度的决策方法研究中存在的问题，提出了一种基于直觉模糊熵和改进的协相关度的决策方法。为准确度量直觉模糊集的直觉性和模糊性，给出了一种改进的直觉模糊熵的公式，概括并推广了原有的一类直觉模糊熵的公式，并讨论了其相关性质。然后由概率统计中相关系数的构造思想，改进了直觉模糊集协相关度的定义，构造了直觉模糊集与理想对象之间的相关系数以及得分函数，由此给出了一种改进的基于直觉模糊信息的多属性决策方法，最后通过实例计算验证了该方法的有效性和可行性。

直觉模糊集；直觉模糊熵；协相关度；得分函数

2016-10-20

2017-01-17

1002-8331（2018）06-0247-05

A

TP18

10.3778/j.issn.1002-8331.1610-0235

国家自然科学基金（No.61502262）。

王斌（1963—），男，博士，教授，研究生导师，主要研究方向：知识发现，博弈论及应用，E-mail：wb769@sina.com；王哲辰（1993—），男，博士研究生，主要研究方向：智能控制；周炜（1981—），男，博士，讲师，主要研究方向：信任认证，信息安全；郝天鹏（1991—），男，硕士研究生，主要研究方向：数据挖掘，知识发现。