解不定信赖域子问题的Heun三阶算法

董建新，李琳俊，王希云

1.长治学院数学系，山西长治046011

2.太原科技大学应用科学学院，太原030024

解不定信赖域子问题的Heun三阶算法

董建新1，李琳俊2，王希云2

1.长治学院数学系，山西长治046011

2.太原科技大学应用科学学院，太原030024

1 引言

无约束优化问题为：

其中f:Rn→R为二次连续可微函数。

求解无约束优化问题时，通常先选择二次函数作为目标函数的近似，然后用信赖域方法[1-2]求解该子问题，即：

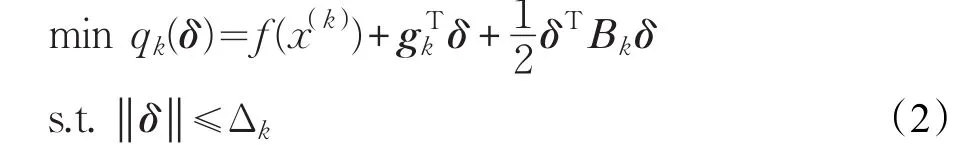
式中，gk∈Rn为当前迭代点x()k处目标函数的梯度，是f(x)在的Hessian矩阵或者是此矩阵的近似形式。

随着信赖域半径Δk的连续变化，子问题的解δ*就形成空间中的一条曲线，即为最优曲线。最优解曲线的参数方程[3]为：

对式（3）两边求导，可确定微分方程模型：

对微分方程模型，可以用求解方程的相关方法构造各种合理的折线近似最优曲线，从而求出子问题的解。这种思想结合了微分方程现有的求解方法和子问题的实际情况，提出了很多有效算法[4-7]，得到很好的应用。当子问题中的Hessian矩阵正定时，有各种效果更好的折线算法，比如常用单折线法[8]、双折线法[9]，不定折线法[10-12]，隐式分段折线法[13]、欧拉切线法[14]等；然而对

Hessian矩阵不定时的求解方法讨论较少。本文参考文献[15-16]，结合Heun三阶方法[17-18]，利用Bunch-Parlett法[3]，对B为不定矩阵的情况进行修正，构造了对称正定矩阵，将不定子问题转化为正定子问题，用新的折线来逼近最优解曲线，从而给出了求解不定信赖域子问题的Heun三阶算法。

2 Heun三阶折线的构造

根据Heun三阶公式，依次计算P0(μ0,δ0),P1(μ1,δ1),…,PN(μN,δN)，连接后便可以得到Heun三阶折线：T=记Heun三阶折线为具体形式如下：

步长h0见式（6）。

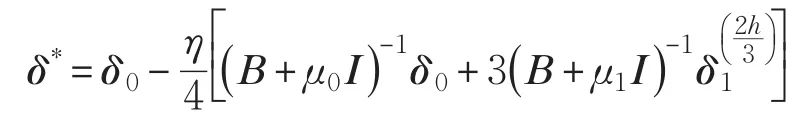
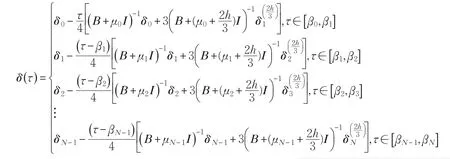
且：

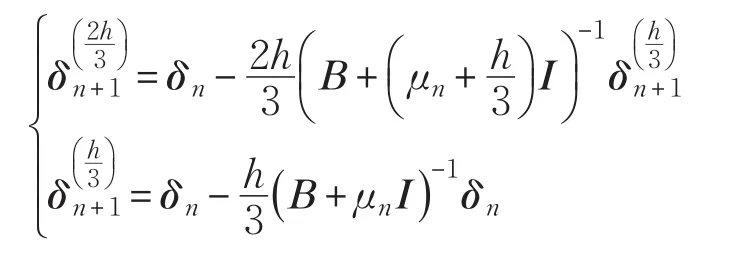
3 算法描述

下面给出Heun三阶算法的具体步骤，其中的步长选取见步骤后的注。

算法步骤：

输入参数梯度g，不定矩阵B，信赖域半径Δ。取：n:=0。

步骤1将不定矩阵B进行Bunch-Parlett分解，有B=LDLT成立，结合矩阵D的特征值情况构造对称且正定的矩阵G，并取B=G-1。

步骤2令δ0=δnp=-B-1g，若，则取：δ*=δ0，停止计算。否则转步骤3。

步骤3令：

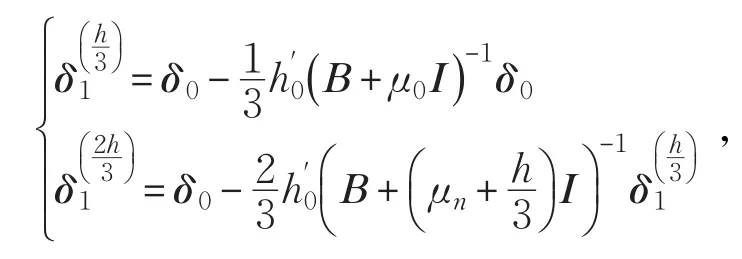
且μ0=0，步长见式（5），转步骤4。

步骤4令：

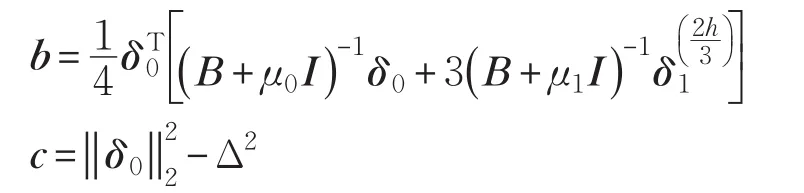
停止计算。否则令：n:=1，转步骤5。

步骤5令：

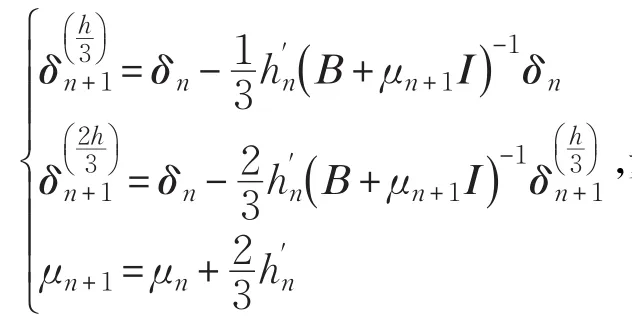
步骤6令：

步长hn见式（8）。

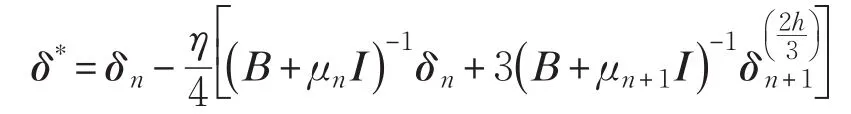
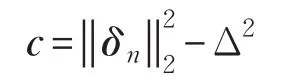
步骤7输出解δ*。

注：算法中步长选取策略如下：

其中：δ0=-B-1g，ε为限制步长，即每一次搜索时可以取到的最大步长为ε，ε越小，求得的最优解δ*越精确。

4 Heun三阶折线路径性质分析

类似欧拉切线路径性质分析[7]，下面给出Heun三阶折线路径的性质分析。

引理1对任意不定矩阵B，在n=1,2,3,…,N-1时，有：成立。

证明用第二类数学归纳法来证明。

（1）当n=1时：

由式（8）知：

（2）假设1＜n≤k时，结论成立；当n=k+1时，有：

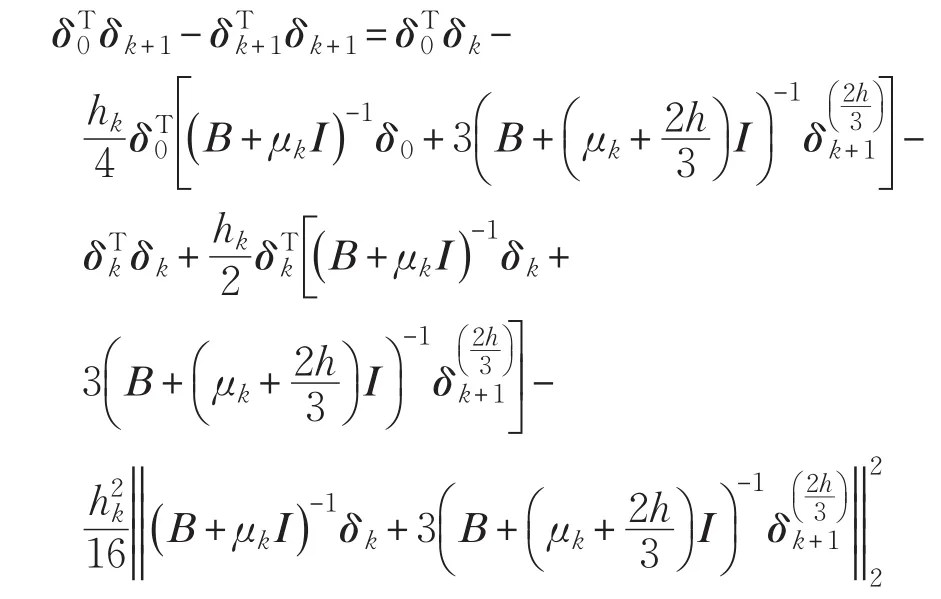
①当

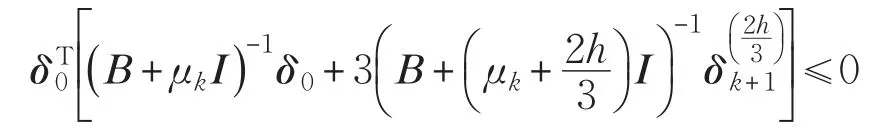
时，有：

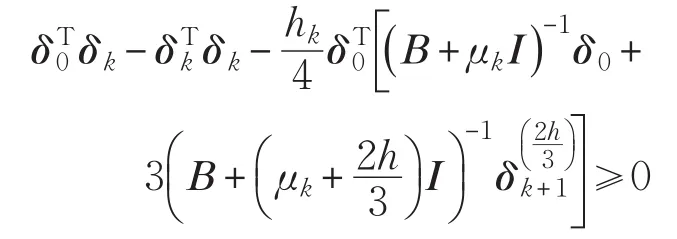
根据式（8）可得：

②当

时，根据式（8）可以得到：

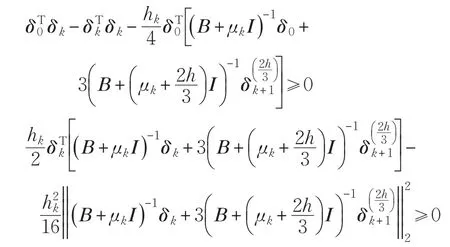
由（1）、（2）得，引理1成立。证毕。

定理1假设B为不定矩阵，且有下式成立：

证明（1）①当即τ∈[]0,h0时，有：

则

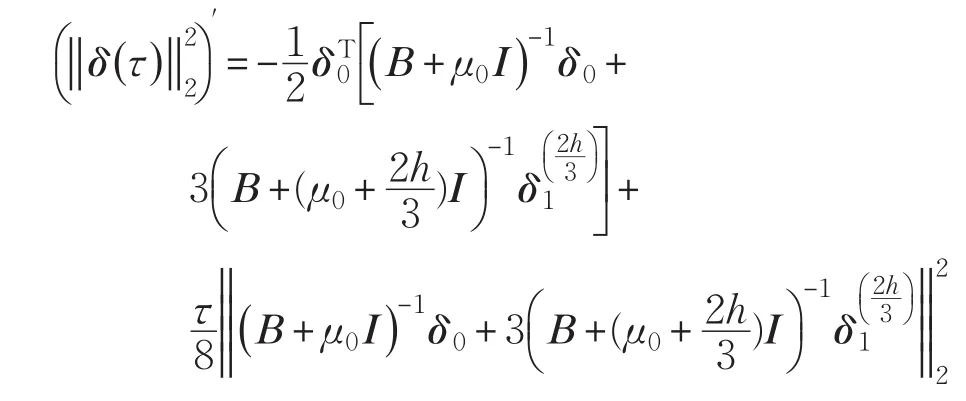
由式（6）：

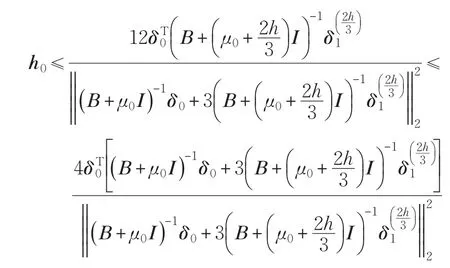
根据式（8）：

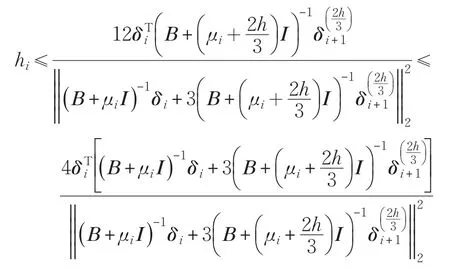
由①、②得：结论（1）成立。

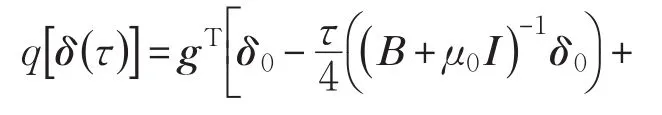
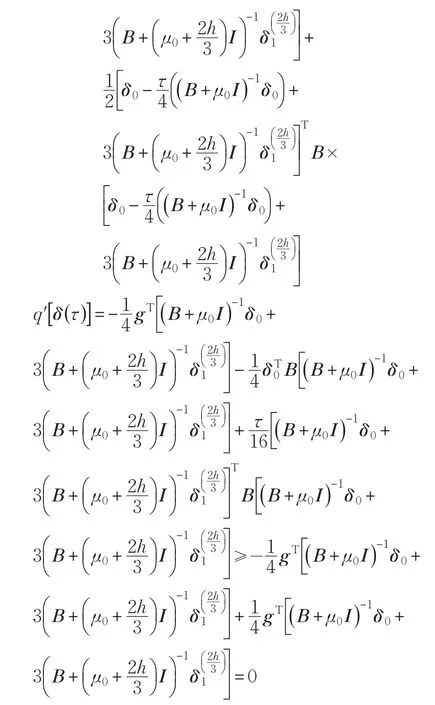
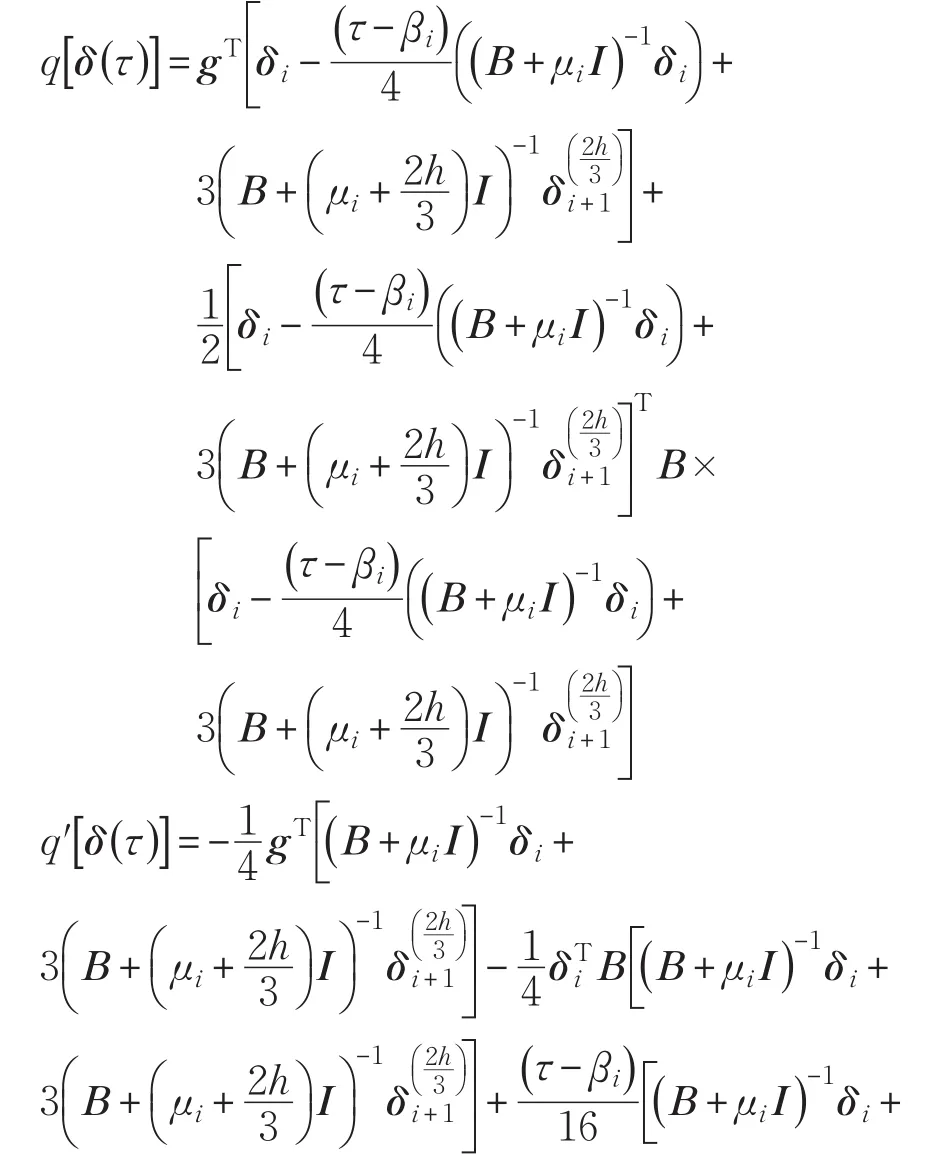
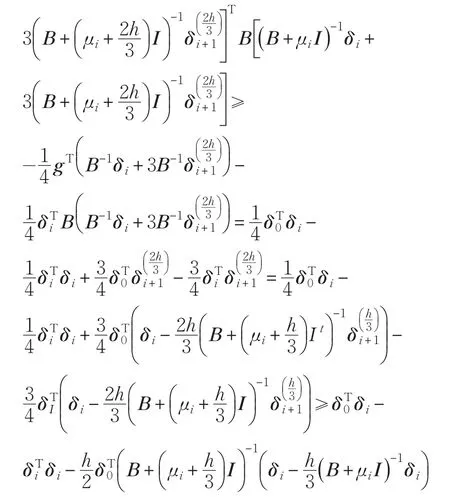
综上，由①、②得，结论（2）成立。证毕。

5 算法的适定性

定理1中的结论（1）说明折线上的近似解是惟一的，结论（2）说明所求出的近似解满足下降条件，由此可保证信赖域算法的全局收敛性，从而得到下面结论。

定理2假设Hessian阵B为不定矩阵，用Heun三阶算法来求解，对于任意信赖域半径Δ，一定可以找到自然数N，使得满足

结合定理1和定理2可以知道：对于任意信赖域半径Δ，Heun三阶折线δ(τ)上确定的近似解存在且唯一；沿着折线δ(τ)可以寻求子问题（2）的最优解δ*，且该点在信赖域边界上取得。

6 数值实验

用以下两个信赖子问题的测试函数[16]，运用Matlab2012b进行数值实验，得到相应的结果，并进行简要分析。

测试函数1：

测试函数2：

实验中，选取不同的信赖域半径Δ，分别用Heun三阶算法和混合折线法来计算不定子问题最优解，并与精确解进行比较。qHD-qHeun表示两种方法所求的最优解的差值。具体结果见表1和表2。

表1 测试函数1的数值结果

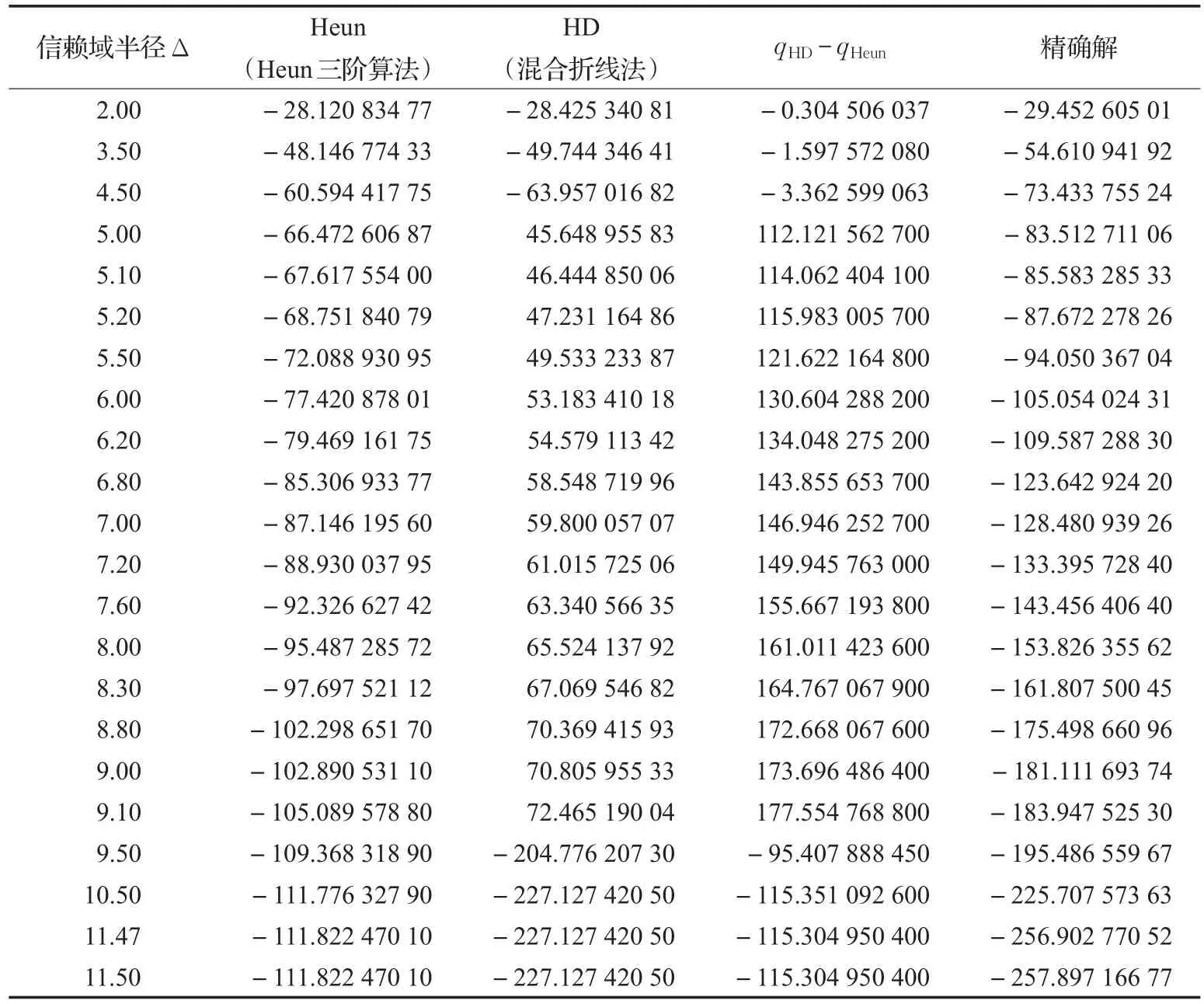
表2 测试函数2的数值结果

从实验数据可以看出，Heun三阶算法有效可行；且当信赖域半径在一定范围内时，Heun三阶算法与混合折线法的差值越来越大，说明在一定约束条件下，Heun三阶算法效果非常好。

7 结论

针对Hessian矩阵不正定的信赖域子问题，构造了对称正定的矩阵，用新的折线来逼近最优解曲线，构造出Heun三阶算法；通过对算法路径性质的分析，理论上证明了算法的适定性；又通过数值实验证明了算法可行并且在一定条件下收敛效果非常好。然而，当信赖域半径接近拟牛顿步长时，新算法优势不再明显，需要以后继续研究。

[1] 袁亚湘，孙文瑜.最优化理论与方法[M].北京：科学出版社，2010.

[2] 李董辉，童小娇，万中.数值最优化算法与理论[M].北京：科学出版社，2010.

[3] 徐成贤，陈志平，李乃成.近代优化方法[M].北京：科学出版社，2002.

[4] Zhou Qunyan，Zhang Chun.A new nonmonotone adaptivetrustregionmethodbasedonsimplequadratic models[J].Journal of Applied Mathematics and Computing，2012，40（1/2）：111-123.

[5] Toint P L，Tomanos D.A multilevel algorithm for solving the trust-region subproblem[J].Optimization Methods and Software，2009，24（2）：299-311.

[6] Zhu X T，Xi M，Sun W Y，et al.A new nonmonotone BB-TR method based on simple conic model for large scale unconstrained optimization[J].Numerical Mathematics A Journal of Chinese Universities，2016，38（2）：172-192.

[7] 李亮.一类求解信赖域子问题的欧拉算法[D].太原：太原科技大学，2014.

[8] Powell M J D.A hybrid method for nonlinear equations[C]//NumericalMethodsforNonlinearAlgebraic Equations.Rabinowtiz Ped，London：Gordon and Breach，1970：87-114.

[9] Dennis J E，Mei H H W.Two new unconstrained optimizationalgorithmswhichusefunctionandgradient values[J].Journal of Optimization Theory and Applications，1979，28（4）：453-482.

10] 赵英良，徐成贤.解信赖域子问题的切线单折线法[J].数值计算与计算机应用，2000，21（1）：77-80.

[11] 王希云，邵安.一种双割线折线法求解信赖域子问题[J].应用数学，2012，25（2）：419-424.

[12] Zhang Jianzhong，Xu Chenxian.A class of indefinite dogleg path methods for unconstrained minimization[J].SIAM Journal on Optimization，1999，9（3）：646-667.

[13] Chen Jun，Sun Wenyu.Nonmonotone adaptive trust region algorithms with indefinite dogleg path methods for unconstrained minimization[J].Northeast Math Journal，2008，24（1）：19-30.

[14] 邵安，王希云.一种求解不定信赖域子问题的双割线折线法[J].太原科技大学学报，2011，32（6）：483-497.

[15] 赵丹.解信赖域子问题的混合折线法[J].徐州师范大学学报：自然科学版，2009，27（3）：38-41.

[16] 王希云，贾新辉，王子豪.一种改进的隐式Euler切线法[J].应用数学与力学，2017，38（3）：347-354.

[17] 颜庆津.数值分析[M].北京：北京航空航天大学出版社，2006.

[18] 李亮，王希云，张雅琦，等.一种求解二次模型信赖域子问题的休恩算法[J].太原科技大学学报，2014，35（2）：151-155.

DONG Jianxin,LI Linjun,WANG Xiyun.Heun third-order algorithm for solving indefinite trust region subproblems.Computer Engineering andApplications,2018,54（6）：55-61.

DONG Jianxin1,LI Linjun2,WANG Xiyun2

1.Department of Mathematics,Changzhi University,Changzhi,Shanxi 046011,China
2.School ofApplied Science,Taiyuan University of Science and Technology,Taiyuan 030024,China

For the trust region subproblems,it is modified by Bunch-Parlett method when the Hessian matrix is indefinite.In addition,symmetric positive-definite matrix is also constructed,and the stator problem is transformed into a positivedefinite subproblem.The Heun third-order algorithm is given by using a new polygonal line to approximate the solution curve.Then,the feasibility of this algorithm is theoretically proved by analyzing the properties of path of Heun thirdorder polyline.Finally,the numerical experiments of two test-function show that the algorithm is effective.

trust region subproblems;differential equation model;indefinite matrix;Heun third-order algorithm

针对信赖域子问题，当Hessian矩阵不正定时，利用Bunch-Parlett法对矩阵进行修正，构造了对称正定的矩阵，将不定子问题转化为正定子问题，用新的折线来逼近最优解曲线，给出了求解的Heun三阶算法。通过对Heun三阶折线路径性质的分析，理论上证明了算法的适定性。利用两个测试函数进行了数值实验，结果表明该算法有效。

信赖域子问题；微分方程模型；不定矩阵；Heun三阶算法

2017-07-28

2017-10-27

1002-8331（2018）06-0055-07

A

O221

10.3778/j.issn.1002-8331.1707-0457

国家自然科学基金青年项目（No.61602061）；山西省“131”领军人才工程项目；长治学院校级科研项目（No.201607）。

董建新（1978—），男，讲师，研究领域为运筹优化与数值计算，E-mail：jianxindong@163.com；李琳俊（1991—），女，硕士，研究领域为最优化理论及应用；王希云（1963—），女，教授，研究领域为最优化理论及应用。

◎网络、通信与安全◎