二次函数图像中存在相似三角形的问题解析

山东省日照市东港实验学校 孙承娟

下面我们以几道经典例题的分析方法和解答步骤为例作以说明。

一、分类讨论，体现“对方程与函数、分类讨论思想和方法的考查”

例1 如图所示，抛物线经过点A(4，0)、B（1，0)、C（0，－2）。

图1

（1）求此抛物线的解析式；

（2）P是抛物线第一象限上的一个动点，过P作PM⊥x轴，垂足为M，是否存在点P，使得以A、P、M为顶点的三角形与△OAC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由。

解析：（1）∵该抛物线过点C（0，-2），

∴可设该抛物线的解析式为y=ax2+bx-2，

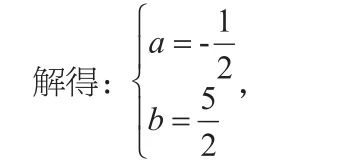
（2）存在，如图2所示，设P点的横坐标为m，则P点的纵坐标为当1＜m＜4时，AM=4-m，

∵∠COA=∠PMA=90°，

△APM∽△ACO，

解得m1=2，m2=4（舍去）， ∴P（2，1）；

图2

类似地可求出当m＞4时，P（5，-2）；当m＜1时，P（-3，-14）。

综上所述，符合条件的点P为（2，1）或（5，-2）或（-3，-14）。

评注：求相似三角形的第三个顶点的坐标时，先要分析已知三角形的边和角的特点，进而得出已知三角形是否为特殊三角形，再根据未知三角形中已知边与已知三角形的可能对应边进行分类讨论，从而体现出“对方程与函数、分类讨论思想和方法的考查”。

二、数形结合，培养“转换”思想和意识

例2 如图3所示，已知：抛物线y=ax2﹣2ax+c（a≠0）交x轴于A、B两点，A点坐标为（3，0），与y轴交于点C（0，4），以OC、OA为边作矩形OADC交抛物线于点G。

（1）求抛物线的解析式；

（2）抛物线的对称轴l在边OA（不包括O、A两点）上平行移动，分别交x轴于点E，交CD于点F，交AC于点M，交抛物线于点P，若点M的横坐标为m，请用含m的代数式表示PM的长；

（3）在（2）的条件下，连接PC，则在CD上方的抛物线部分是否存在这样的点P，使得以P、C、F为顶点的三角形和△AEM相似？若存在，求出此时m的值，并直接判断△PCM的形状；若不存在，请说明理由。

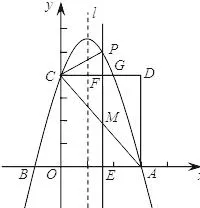
图3

解析：（1）∵抛物线y=ax2-2ax+c（a≠0）经过点A（3，0），点C（0，4），

（2）设直线AC的解析式为y=kx+b，

∵A（3，0），点C（0，4），

∵点M的横坐标为m，点M在AC上，

（3）在（2）的条件下，连接PC，在CD上方的抛物线部分存在这样的点P，使得以 P、C、F为顶点的三角形和△AEM相似。理由如下：

要使以P、C、F为顶点的三角形和△AEM相似，只需△PFC∽△AOC即可。

分两种情况讨论：

①若△PFC∽△AOC，则PF:CF=OA:OC，且∠PFC=∠AOC=90°，即

在直角三角形CMF中，∵∠CMF+∠MCF=90°，∴∠PCF+∠MCF=90°，即∠PCM=90°，∴△PCM为直角三角形。

②若△PFC∽△COA，则PF:CF=OC:OA，且∠PFC=∠AOC=90°，即∶m=4∶3，

∵m≠0且m≠3， ∴m=1。∵△CFP∽△AEM，∴∠CPF=∠AME，∵∠AME=∠CMF，∴∠CPF=∠CMF，∴CP=CM， ∴△PCM为等腰三角形。

综上所述，存在这样的点P，使以P、C、F为顶点的三角形与△AEM相似，此时m的值为或1，△PCM为直角三角形或等腰三角形。

评注：本题是综合性很强的题目，需要运用“转换”的思想。学会数学“转换”或“转化”，有利于实现复杂问题简单化，从而可以较快地提高学习质量和数学能力。就本题而言，训练学生运用数形结合思维分析解决问题，有助于将“转换”思想内化成学生的一种数学解题策略和意识。