一种基于SNAM二值图像表示方法的正方形子模式搜索策略

宫海晓，贺 杰

(1.2梧州学院 信息与电子工程学院，广西 梧州 543002)

0 引言

图像表示[1]是图像处理领域中的一个重要的研究方向，随着多媒体技术的发展，图像数据量变得越来越大，为了减少数据存储量和提高处理效率，陈传波教授提出了一种新的图像表示方法，即非对称逆布局模型的图像表示方法[2]，该方法不仅解决了四元树等图像表示方法存在的对称分割问题，而且在降低图像的存储空间、提高算法的运算速度等方面都取得了显著的成效。后续研究者陆续提出了基于矩形、三角形、梯形等的图像表示方法，其中贺杰教授在NAM的基础上提出了基于正方形的非对称逆布局表示方法[3]，即SNAM图像表示方法，该方法通过光栅扫描[4]的方式对正方形子模式进行搜索，然后对搜索到的子模式进行逆布局，最终形成了图像的表示。

光栅扫描适用于块状特征不明显的图像，是一种通用的扫描方式，但该扫描策略对SNAM的正方形子模式的搜索具有一定的局限性，因此，作者针对正方形子模式独有的结构特征，提出了对角扫描策略。

1 对角扫描的过程原理

对角扫描方式依据正方形独特的结构特征，通过判断对角的两个像素点特征是否一致进行搜索，具体过程为，在二值图像矩阵中的第一行开始找到一个像素值为0且未被标记的点，把此点当基准点A，A的坐标值为(x，y)。以A为正方形的左上角顶点开始寻找第一个正方形，以i(i=1，2，3...)为正方形边长开始搜索；接下来开始扫描基准点A正右方对应的顶点B和正下方的对应顶点C的值是否同时为0(B和C点正方形左上角顶点存在一定的数学关系，B和C在一条对角线上)，其中j是控制在i内的变量边长，(x+j-1，y+i)、(x+i，y+j-1)分别对应B点和C点的坐标。B和C点的值若都为0，则判断B点和C点的横坐标和纵坐标的差值是否为x-y；当条件不成立，继续寻找下一个新的基准点A。若B，C同时为0则判断正方形的最后一个点D的像素值是否为0，为0，判断正方形是否已经到达边界，不为边界则i值变化，j随着i变化，继续类似于B、C的对角点值进行更大的正方形搜索；否则记录此次所能形成的最大正方的数据。不断重复上述描述的扫描过程，直到所有正方形子模式搜索完成。

图1(a)是一幅原始二值图像，图像中黑点代表像素值为0，白点代表像素值为1。以第一行所在位置设为坐标轴的x轴，第一列所在位置为y轴，则第一行和第一列形成了一个二维的坐标轴。第一个点值从(1，1)开始进行扫描。图1(b)是反角扫描方式扫描过程示意图。

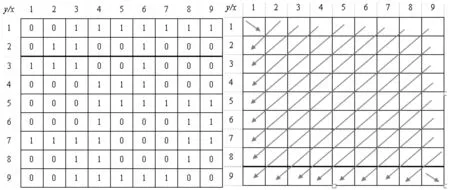
(a)原始二值图像 (b)对角扫描方式扫描过程走向图1 对角扫描正方形子模式算法的解析

2 对角扫描算法的编码设计

首先定义正方形、线段以及孤立点等子模式，对于一幅二值图像的矩阵，依照对角扫描方式的过程，从二值图像的矩阵中提取出黑色像素形成的大小不同的正方形、长短不同的线段和孤立点，并记录下这些子模式的数据。

对角扫描算法的详细编码步骤如下：

步骤1：以x，y为变量，用两层嵌套循改变像素值的变化，其中变化范围为1到n。

步骤2：定义一个标记变量flag并赋给初值0，从图像矩阵的起始点开始找到第一个像素值为0且未被标记为2的点。把坐标值(x，y)赋给(sp_x，sp_y)。

步骤3：定义一个循环变量i用于控制正方形的边长变化，把i值赋给开始定义好的变量len。

步骤4：判断标志变量flag是否为1，值为1，则跳出i循环，跳到步骤(1)；否则继续下一步。

步骤5：判断能形成正方形对角顶点所在位置的像素值是否为0，其中有不为0，说明此循环中判断的正方形不能形成，要返回上一步记录比这个小的正方形，即跳到步骤(10)；否则继续下一步。

步骤6：判断对角的之间的坐标值的横纵坐标之间的差值是否为0(为零说明最后一个顶点为黑点则能形成本次循环的最大正方形)，为0继续下一步；不为0则返回步骤(5)继续判断下一对对角点。

步骤7：判断正方形的最后一个像素点是否为0，为0则继续下一步判断；否则跳到步骤(10)进行判断。

步骤8：判断步骤(7)的最后一个像素点是否为以(x，y)为左上角顶点所达到最大正方形的边界点，是边界点继续下一步；否则回到步骤(3)，i的值增1进入下一个循环。

步骤9：判断边长变量len是否大于0，大于0能形成一个有效的正方形则计数变量Num的值增加1，把定点坐标(sp_x，sp_y)和边长值len存到元胞数组中，然后用两个嵌套循环把此正方形所包含的像素值点全部赋值为2作为标记。返回步骤(2)，继续寻找下一个正方形，直到所有的图像模型中的正方形子模式全部被抽取出来为止。

步骤10：最后一个点不为黑点，不能形成此循环内的最大正方形，要把标记变量flag赋值为1，中断此循环，正方形边长变量的值len减1，并返回步骤(9)进行记录上一个形成的正方形。

线段和孤立点搜索的算法步骤类似，在此就不再重复介绍。

3 对角扫描算法的应用举例

图2(a)是一幅大小为9×9的原始二值图像，图2(b)运用对角扫描方式进行对图像(a)的NAM正方形子模式搜索逆布局结果，从原图中抽取出了5个正方形子模式、2条线段和2个孤立点。

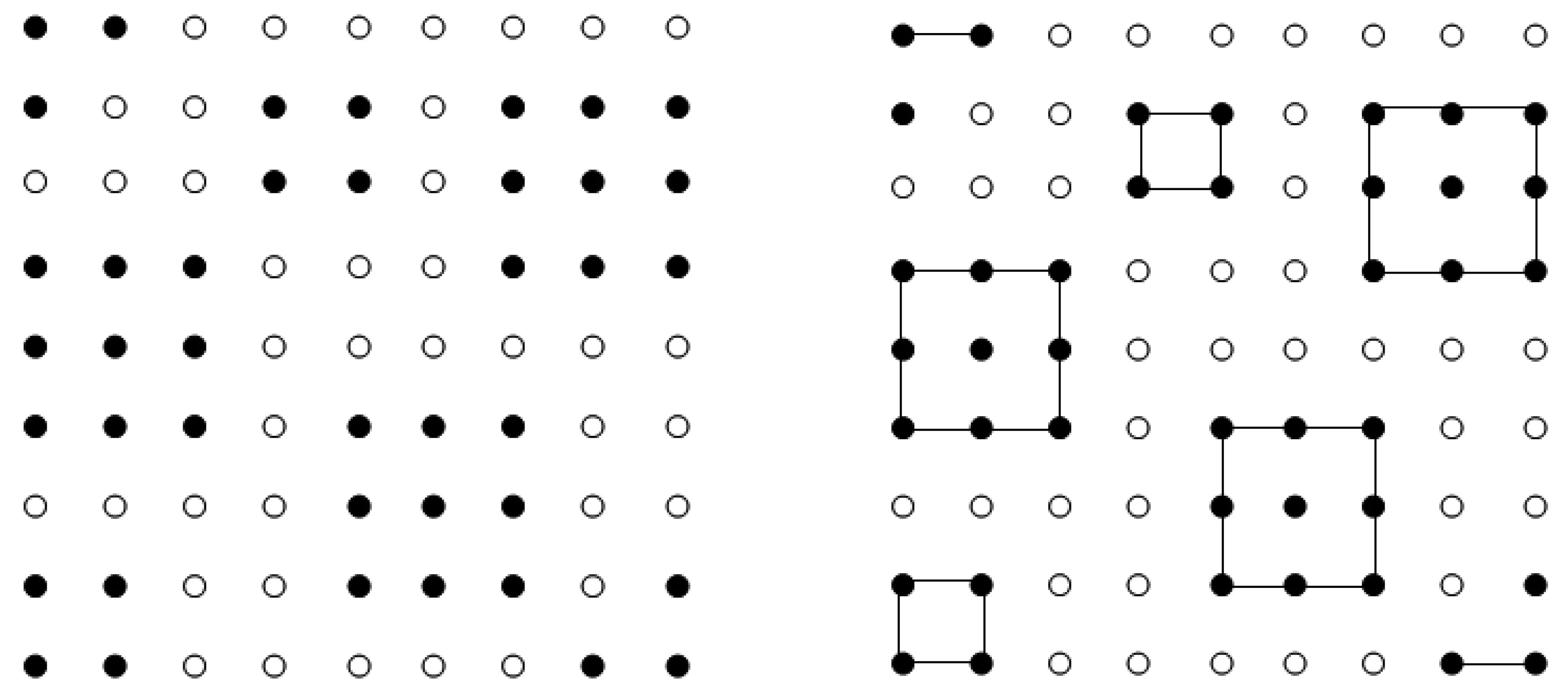
(a)9×9的原始二值图像 (b)反对角扫描正方形逆布局结果图2 对角扫描策略对二值图像正方形逆布局的过程

在搜索过程中产生的数据，对于正方形子模式，将左上顶点坐标和边长存储即可。线段则把起始端点的坐标和长度存储即可。孤立点将坐标存储即可。图3是对二值图像的正方形对角扫描的逆布局存储结果。下页图3(a)是所有子模式的搜索结果，即5个正方形，2条线段和2个孤立点，下页图3(b)子模式的存储方式，如正方形子模式s1，其存储记录为s1={(2，4)，1}，表示其左上角顶点坐标为(2，4)，边长为1个的正方形所包含的像素点；线段子模式l1，其存储记录为l1={(1，1)，1}，表示其线段起始顶点坐标为(1，1)，长度为1个的线段所包含的像素点；孤立点子模式p1，其存储记录为p1={(2，1)}，表示其坐标为(2，1)的像素点。

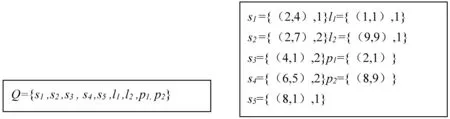
(a)二值图像Q的正方形子模式表示结果 (b)算法产生数据的存储结果图3 二值图像中正方形子模式存储结果

4 算法分析

对角扫描算法的时间复杂度主要取决于算法中的4个嵌套循环，因此对于一幅规模为N的二值图像P，N就是P的像素总数，利用对角扫描算法进行编码，算法消耗时间与像素总数N成正比，因此反对角扫描算法的时间复杂度为O(Nn4)。

在对角扫描算法中，用于存储输入数据和在执行过程中缓存的存储空间对算法的复杂度的分析影响较小，算法在执行过程中所需要的额外空间与图像像素总数大小的有着正比的关系，图像的像素总量为N，则对角扫描算法的空间复杂度可以表示为O(N)。

而在数据量方面，对于一幅大小为n×n的二值图像模型，在对角扫描算法编码后产生Ns个正方形子模式，Nl条线段，Np个孤立点，总的子模式数据量设为A，依据贺杰教授的SNAM表示方法，存储这些子模式的存储空间正方形需要2n位、线段2n位、孤立点n位。因此总的存储空间为：As=2nNs+2nNl+nNp。

如采用线性四元树LQT表示方法编码[5]，文献1指出，记录一个像素点需要3n-1位的空间，假设黑色像素数量是NLQT，ALQT表示数据总量，则总的数据量为：ALQT=(3n-1)NLQT。

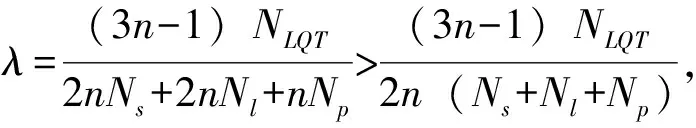
4 总结

本文以SNAM图像表示方法为依据，利用正方形的特殊形状结构，在光栅扫描的基础上进行了改进，提出了对角扫描策略，并详细分析了该扫描算法的原理、对算法进行了编码设计，然后结合实例进行详细阐述，最后在理论上对算法的存储结构、数据量、时间复杂度等几个方面[7]，与经典的线性四元树表示方法进行了比较和分析。理论分析和实验结果表明，基于对角扫描的SNAM图像表示方法相对于线性四元树表示方法，在子模式数量、搜索速度等方面都具有一定的优势。