基于机载LiDAR多回波类型森林叶面积指数反演研究
谢 杰 ,邢艳秋 ,尤号田 ,田 昕 ,安立华,姚松涛
(1. 东北林业大学 森林作业与环境研究中心,黑龙江 哈尔滨 150040;2. 中国林业科学研究院 资源信息研究所, 北京 100091)
森林通过光合作用、呼吸作用和蒸腾作用实现了物质能量的交换[1],而叶片是光合作用的主要载体,是生物生产力转换的关键[2-3]。叶面积指数(Leaf Area Index,Lai)用来表征叶片的疏密程度[4],是反映植被生长状况的重要指标[5],被定义为单位地表面积上单面植物光合作用面积的总和[6-8]。
激光雷达(Light Detection and Ranging,LiDAR)作为一种先进的主动遥感技术,既能弥补光学遥感在反演植被结构参数上的不足[9],又能够穿透植被冠层,获取地面的三维结构信息及植被的垂直结构信息[10],现已广泛运用于林业研究[11]。近年来,国内外学者利用LiDAR数据对森林Lai进行了大量的研究[12-13]。如:李文娟等[14]基于机载LiDAR点云数据,利用样方内地面点数量与样方内总点云数量的比值,求得激光穿透指数(Laser Penetration Index,Lpi)用于估测森林Lai,估测精度R2=0.730。Luo等[15]利用机载LiDAR强度数据,提取样方Lpi用于估测森林Lai,结果表明基于点云强度Lpi的估测精度R2为0.825,RMSE为0.165。通过对先前类似研究进行分析发现,由LiDAR数据计算得到的Lpi能够有效估测森林Lai,但在计算过程中常采用地面点云强度总和与样方点云强度总和之比,未曾考虑多回波强度数据间的差异。因为激光脉冲在穿透森林冠层时,会造成部分能量损失,因而多次回波强度数据间的可比性相对很小。
本研究以内蒙古依根农场机载LiDAR点云数据为基础研究数据,通过对点云数据进行去噪、分类、强度校正及高程归一化等处理,从中依据回波类型的不同分别提取了点云数量和点云强度的激光穿透指数,之后利用提取的激光穿透指数借助多元线性回归算法对森林Lai进行估测,以期实现森林Lai的高精度估测。
1 研究区概况与数据获取
1.1 研究区概况
研究区位于内蒙古呼伦贝尔市西北部、额尔古纳市东南部的上库力农场(120°36′50.48″~120°52′56.53″E, 50°21′11.08″~ 50°24′32.00″N),东与牙克石市为邻,东南与陈巴尔虎旗相连,西和西南与拉布大林农牧场接壤,北与三河马场交界,如图1所示。地处较复杂的山岳地形,属于寒温带大陆性季风气候,海拔在600~700 m。山脉丘陵阴坡广泛分布着以白桦Betula platyphylla为主的天然次生林,其中混生树种主要有落叶松Larix gmelinii和樟子松Pinus sylvestris等,林下灌层主要由石棒绣线菊Spiraea media、筐柳Salix linearistipularis等组成。
图1 研究区位置Fig. 1 Location of study area
1.2 机载LiDAR数据获取
2012年8月26日由飞机搭载Leica ALS60机载激光雷达扫描系统,相对飞行高度1 300 m,平均速度为160 km/h,当天天气状况良好。激光脉冲波长为1 064 nm,最大扫描频率200 kHz,扫描方式为线性扫描,平均点云密度在2~4个脉冲点/m2,光斑大小0.22 m,共获取东西方向22个条带的数据。数据采用标准LiDAR存储格式las1.2,该数据格式存储了点云的坐标值、高程值、回波强度、回波次数、自定义分类等信息。
1.3 野外数据获取
为了避免野外数据采集时偶然因素造成的影响以保证模型的稳定性,于2012年8月在研究区中部连续布设了80块大小为10 m×10 m的方形样地,样地内分布树种均为白桦。在研究区开阔地带架设基站,采用型号为Juno SB的手持式GPS对样地的4个角点和中心点进行定位,之后利用基站数据对手持GPS坐标进行差分运算,使最后差分定位精度在厘米级。与此同时,利用Lai-2000冠层分析仪分别对每块样地的中心点及角点进行测量,取多次测量的平均值作为样地Lai的实测值,为了避免林下灌木、杂草的影响,野外测量Lai时,Lai-2000冠层分析仪始终处于距离地面1.3 m的位置。野外Lai采集统计结果如表1所示。

表1 野外Lai数据基本统计量Table 1 Basic statistics of measured Lai data
2 研究方法
2.1 LiDAR数据去噪
激光雷达飞行时,收集的数据不仅包含所需要的有用数据,同时也会产生噪声点,这部分噪声点通常为孤立点,往往是高于地物点或者是低于地面点。本研究在TerraSolid软件平台上,利用孤立点算法,以某一点为球心,给定相应的阈值半径,若此球内无其他点,即认为此点为噪声点,最后人工检查修正。
2.2 LiDAR点云能量强度校正
由于大气传输过程中的衰减、目标物与发射器之间的距离等原因会产生误差,为减小误差累积,在研究前对点云能量进行近似校正,利用Baltsavias等[16]研究激光雷达能量方程进行近似校正。对于本研究采用同一系统进行数据采集,飞机水平飞行,数据获取时天气晴朗,近似认为硬件参数不变,只考虑目标的面积、反射率以及距离对接收能量的影响,传感器接收的能量与距离的四次方成反比[17-18]。为了排除距离对计算结果产生影响,按照简化公式(1)进行强度校正。

式中,Rs是参考距离(m),I是回波强度值(w),I(Rs)是校正到参考距离处的强度值(w),R是发射器与目标之间的距离(m),Hf、Hp分别为飞行绝对航高和回波点的高程(m),α是瞬时扫描角(°)。
2.3 LiDAR数据分类
采用不规则三角网滤波算法进行点云分类,插值算法生成数字高程模型,利用所有点云高程值与数字高程模型做差,得到归一化后的点云。然后对归一化后的数据进行进一步的划分,将高于1.3 m的点记为植被点,低于1.3 m的点记为地面点。分别统计样方内的所有点云、植被点、地面点。在研究区中,大部分为白桦林,白桦生长呈圆锥形,堆叠枝叶较少,通透性较好,使得LiDAR数据多为首次回波(包括单次回波)和末次回波点,中间回波数量极少,因此本研究将点云按照首次回波(包括单次回波)、末次回波进行统计,同时统计各类点云的能量值。
2.4 基于点云数量的参数提取
本研究根据点云的回波类型,对激光穿透指数进行了细分,得到基于点云数量的多回波次数的激光穿透指数nLPIfirst、nLPIlast、nLPIcan。其中nLPIfirst为首次回波数量激光穿透指数,nLPIlast为末次回波数量激光穿透指数,nLPIcan为冠层回波数量激光穿透指数,计算公式见式3~5所示:
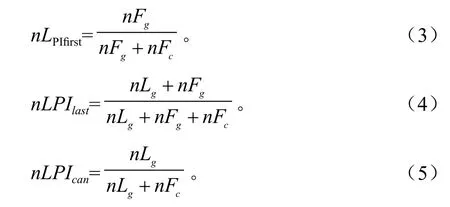
式中,nFg为样方内首次回波(包括单次回波)地面点的数量,nFc为样方内首次回波点(包括单次回波)冠层点的数量,nLg为样方内末次回波地面点的数量。
2.5 基于点云能量的参数提取
冠层孔隙的大小与激光穿透指数有着直接的关系,经过校正后的点云强度值,对于冠层和地面,其强度值与物体表面积成正比,见公式(6),点云强度的值能够较好的反映出冠层孔隙的大小。

式中I表示强度值,A表示面积,ρ为物体反射率。
设地表反射率为ρg,植被层反射率为ρc,因此植被反射率比值系数来代替真实地表反射率,即由于地面单次回波强度和冠层单次回波强度值有一定的波动范围,但仍然在一个定值附近变化,通过计算两种单次回波强度值的最大概率分布时对应的强度值的比值,其计算公式如公式(7):
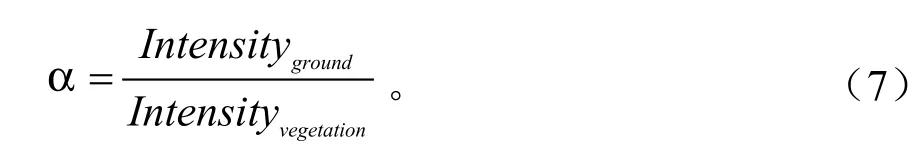
本研究区与邢艳秋等[19]研究区相同,且源数据也相同,根据邢艳秋等[19]研究结果,确定研究区内α值为3.0。
当激光点云出现首次回波和末次回波时,首次回波点和末次回波点的的能量强度值由反射面积决定,面积不同,回波的强度值不同。基于点云数量的Lpi不能够很好的将由于面积不同而引起的差异反映出来。而激光在穿透冠层时,会有一部分的能量损耗,多次回波中不同点云之间的能量可比性很小。因此本研究基于多回波类型提取点云能量的激光穿透指数iLPIfirst、iLPIlast、iLPIcan,其中iLPIfirst为首次回波数量激光穿透指数,iLPIlast为末次回波数量激光穿透指数,iLPIcan为冠层回波数量激光穿透指数,计算公式详见式8~10所示:
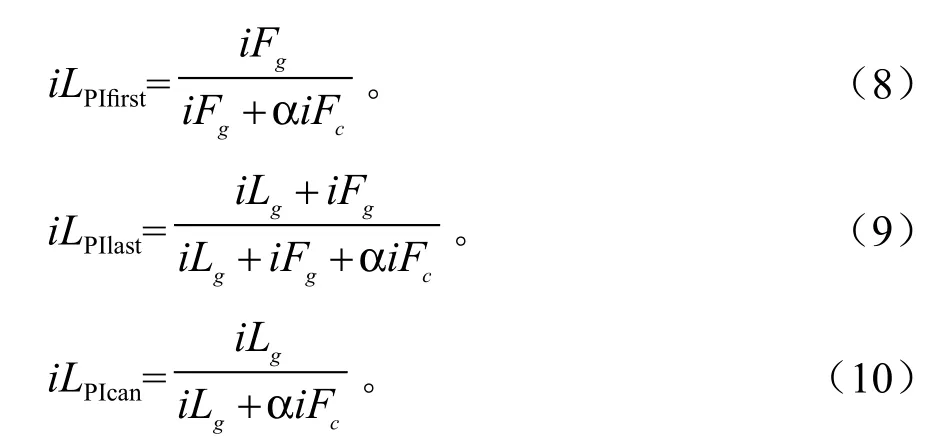
式中,iFg为样方内首次回波(包括单次回波)地面点的强度值,iFc为样方内首次回波(包括单次回波)冠层点的强度值,iLg为样方内末次回波地面点的强度值,α为植被反射率比值系数。
iLPIfirst排除了末次回波对激光穿透指数的影响,LiDAR首次回波包含的信息较多,将直接反映出首次回波对Lai的影响。为了增加对冠层小孔隙的灵敏度,iLPIlast的地面回波点采用首次回波地面点和末次回波地面点之和。iLPIcan反映冠层的信息,利用末次回波地面点和首次回波植被点对冠层穿透指数进行计算。
2.6 LAI模型建立及精度评价
本研究拟对提取的6个变量建立模型。在野外采集的80个样方中随机选取50个用于建模,余下30个用于预测模型精度评价。假定激光穿透指数与Lai具有线性关系,模型公式如式(11):

式中:k为斜率;e为误差项;Lpi为激光穿透指数。
本研究在单变量回归模型的基础上,尝试采用多变量回归模型,多变量回归模型往往存在变量共线性问题,本研究采用方差扩大因子(Variance In fl ation Factor,Vif)来评价自变量之间的共线性问题,见公式(12)。方差扩大因子(Vif)描述了自变量之间共线性的严重程度,值越大表明共线性越严重,一般以小于10为判断依据,即当Vif<10时,表明自变量之间不存在共线性问题,反之当Vif>10则存在严重的共线性问题[12]。

式中:Vifj为自变量Xj的方差扩大因子,R2j为自变量Xj对其余p-1个自变量的复决定系数。
预测模型精度评价主要用决定系数R2,其值越大,说明建模精度越好。预测模型精度采用平均绝对偏差(Mean Absolute Deviation,Mad)来评价,其值越小,说明预测精度越高[20]。
3 结果与分析
3.1 LiDAR点云处理结果
激光点云预处理后,对点云进行分类及高程归一化处理,得到样方原始点云,根据回波次数得到样方首次回波地面点、末次回波地面点、首次回波植被点、末次回波植被点,如图2所示:

图2 激光雷达点云数据Fig.2 Airborne LiDAR point cloud data
从图1中可以看出,激光雷达能够穿透森林冠层到达地面,能够很好地反映出森林的垂直结构信息。地面点被分为首次回波地面点和末次回波地面点,首次回波地面点和末次回波地面点各占有一定比例,可以间接反映出森林冠层情况。首次回波植被点明显多于末次回波植被点,这对于激光束来说末次回波点多落在地面上,只有少量较密集冠层能够阻挡激光束末次回波点,这也与树种有关,在研究区中,大部分为白桦林,白桦生长呈圆锥形,堆叠枝叶较少,通透性较好,使得末次回波植被点相对较少。
3.2 单变量模型估测结果
对6个变量分别建立模型,拟合结果如图3所示。
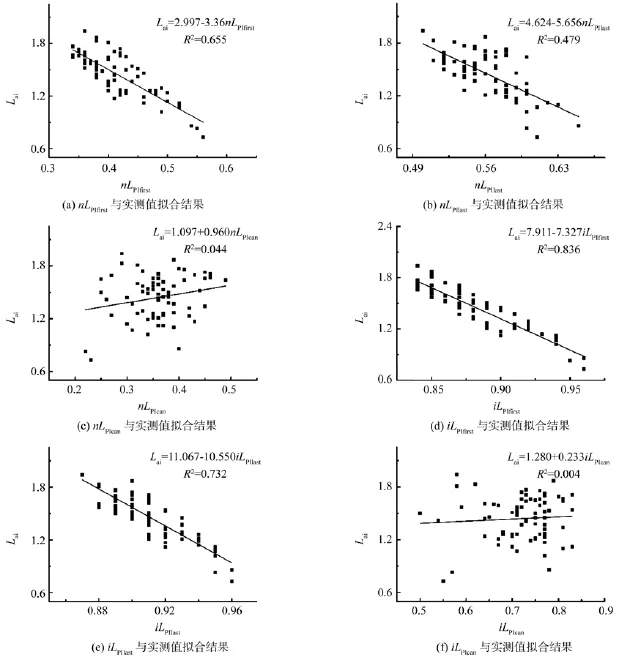
图3 单变量模型建模精度Fig.3 Univariate empirical model estimation results
从图3中可以看出,实测Lai与各激光穿透指数之间大多为负相关关系,R2在0.004~0.836之间。对于变量nLPIcan、iLPIcan而言,决定系数R2低,两者与Lai之间并无明显的线性关系,而其余4个变量均表现出一定的线性关系。Lai随着nLPIfirst、nLPIlast、iLPIfirst、iLPIlast的增加而减小,这种规律符合实际情况,Lai越小,激光穿透率越大。对剩下的30个样方数据进行预测,nLPIfirst、nLPIlast、iLPIfirst、iLPIlast模型的预测精度见图4。
通过表2可以看出,模型精度最高的为iLPIfirst模型,其R2达到了0.836,其模型预测精度也最高,Mad=0.091。iLPIlast、iLPIfirst、nLPIlast反演精度次之,预测精度也随之降低。综合单变量模型结果,单变量iLPIfirst模型最好,即:Lai=7.911-7.327iLPIfirst。
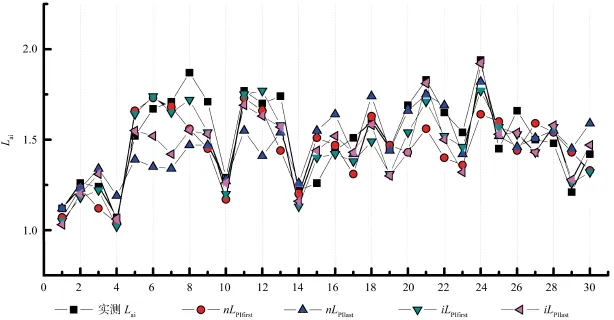
图4 单变量参数模型验证样方预测值与实测值Fig.4 Univariate parameter model veri fi cation of sample prediction and measured value

表2 单变量模型反演精度评价Table 2 Accuracy evaluation of single variable empirical model inversion
3.3 多变量模型估测结果
为了进一步的挖掘变量之间的信息,本研究尝试利用多变量模型来反映与Lai的关系,多变量回归模型能够包含更多有解释力的变量,避免遗漏变量偏差问题。为了解决解释变量共线性的问题,将共线性变量排除,采取逐步回归法得到多变量回归模型,剔除严重共线性的变量组合,最终得到两组符合条件的结果,如表3所示。
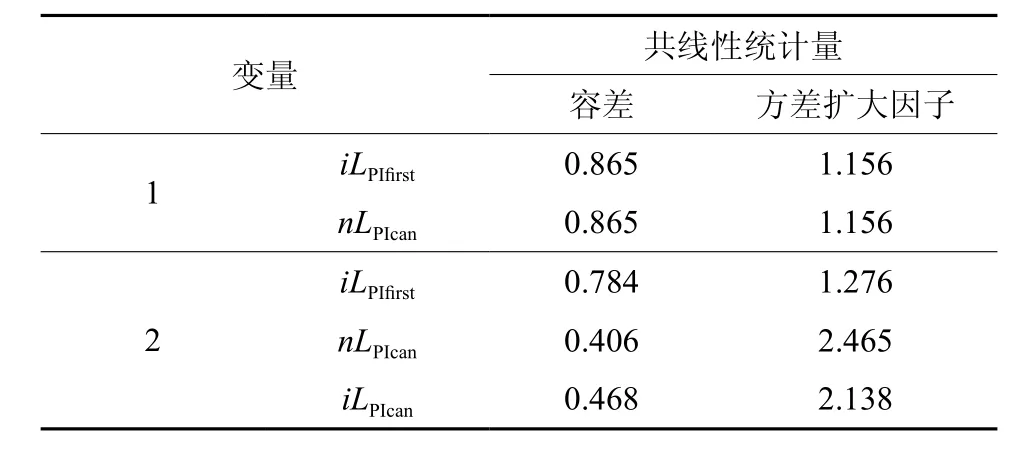
表3 多元回归分析变量多重共线性检验Table 3 Multivariate linear regression analysis of variables
从表2中可以看出,剔除线性相关较大变量后,得到两组多元回归变量,iLPIfirst,nLPIcan和iLPIfirst,nLPIcan,iLPIcan,对两组变量进行拟合,得到的拟合结果如表3所示,预测精度如图5所示。
对比表2和表4可以看出,多变量回归模型的精度都高于单变量回归模型,R2均大于0.85,Mad都低于0.09。相比于单变量回归模型,多变量回归模型能够更好的反映森林叶面积指数,得到了较好的精度。对比单变量iLPIfirst模型和两个多变量模型。单变量iLPIfirst模型利用iLPIfirst参数很好的估计了森林叶面积指数,而多变量iLPIfirst、nLPIcan模型,相比于单变量iLPIfirst模型,加入了nLPIcan参数,反演精度有提高。单看nLPIcan单变量与Lai的关系,他们没有显著相关性,说明变量nLPIcan包含了森林Lai的相关信息,但是与Lai不是简单的线性关系。变量iLPIcan的加入,使得多变量iLPIfirst、nLPIcan、iLPIcan模型相比于多变量iLPIfirst、nLPIcan模型精度提高了,iLPIcan包含许多森林Lai信息,能够很好地和iLPIfirst共同反演森林Lai。

表4 多元回归分析变量模型及精度评价Table 4 Multivariate regression analysis model and precision evaluation
4 结论与讨论
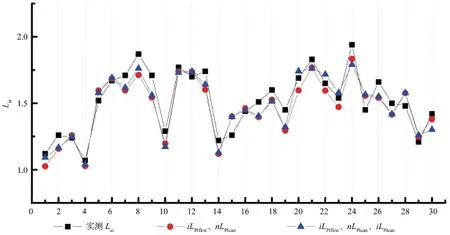
图5 多变量参数模型验证样方预测值与实测值Fig. 5 Multivariate parameter model veri fi cation of sample prediction and measured value
目前,利用遥感技术估测森林叶面积指数已经得到广泛运用,小光斑激光雷达作为一种主动遥感技术,为森林叶面积指数的估测提供新的方法。本研究通过对机载激光雷达点云数据进行去噪、强度校正、高程归一化、多回波类型分类等处理,充分利用激光雷达点云数据中多回波类型之间所含信息的差异,提取基于多回波类型的激光穿透指数,应用这些参数对森林Lai进行反演,得到以下结果:
1)单变量模型中基于点云能量首次回波的iLPIfirst反演的精度最高,其次是基于点云能量末次回波的iLPIlast,二者均高于基于点云数量提取的Lpi的反演结果。结果表明:相比于点云数量,LiDAR点云能量信息包含了更多有关森林叶面积指数的信息,能够更好地反演森林叶面积指数。此结论与骆社周等[21]研究结果类似,骆社周等[21]利用校正能量提取Lpi用于反演森林Lai,结果估测精度(R2=0.825)高于点云数量提取Lpi反演森林Lai的估测精度(R2=0.803)。
2)反演模型中多变量模型反演精度要高于单变量模型反演精度。多变量模型中,利用iLPIfirst、nLPIcan、iLPIcan3个变量的反演模型精度最高,R2为0.883。邢艳秋等[19]利用经过强度校正后的LiDAR点云,通过对样方内点云进行分束,得到样方内所有单束Lpi后求其均值LPImean,用于反演森林Lai,结果R2为0.80,低于本研究所用多变量模型的估测精度但高于部分单精度模型的精度。分析其主要原因,本研究进一步细分了首次回波、末次回波、冠层回波的Lpi,得到了多变量回归模型,弥补了单变量解释能力不足的缺陷。多变量模型估测结果从另一个方面说明单变量参数存在一定的局限性,若要得到高精确度的森林叶面积指数,可以联合应用多个变量参数以消除单变量解释能力的不足,进而实现变量间的优势互补。
本研究利用机载LiDAR离散点云数据多回波间的能量信息,估测了白桦林Lai,获得了较好的结果。但由于本研究所用研究区树种结构较单一,所得模型对其它树种的适用性结果未知,因此在未来的研究中应逐渐加入其他树种以验证模型对其他树种的适用性。
[1]Carlson TN, Ripley DA. On the relation between NDVI,fractional vegetation cover, and leaf area index [J].Remote Sensing of Environment. 1998,62(3):241-252.
[2]Chen JM, Rich PM, Gower ST,et al.Leaf area index of boreal forests: Theory, techniques, and measurements[J].Journal of Geophysical Research Atmospheres, 1997,102(D24):29429-29443.
[3]凌成星, 鞠洪波, 张怀清,等. 基于植被指数比较的湿地区域LAI遥感估算研究[J].中南林业科技大学学报, 2016, 36(5):11-18.
[4]孙 华, 罗朝沁, 林 辉,等. 基于k-NN算法的叶面积指数遥感反演[J].中南林业科技大学学报,2016,36(12):11-17.
[5]Bréda NJJ. Ground-based measurements of leaf area index: a review of methods, instruments and current controversies[J].Journal of Experimental Botany. 2003,54(392):2403-2417.
[6]Jonckheere I, Fleck S, Nackaerts K,et al. Review of methods for in situ leaf area index determination. I. Theories, sensors and hemispherical photography[J].Agricultural & Forest Meteorology, 2004,121(1):19-35.
[7]王希群,马履一,贾忠奎,等.叶面积指数的研究和应用进展[J].生态学杂志,2005,24(5):537-541.
[8]Watson DJ. Comparative Physiological Studies on the Growth of Field Crops: I. Variation in Net Assimilation Rate and Leaf Area between Species and Varieties, and within and between Years[J].Annals of Botany, 1947,11(1):41-76.
[9]Wulder M. Optical remote-sensing techniques for the assessment of forest inventory and biophysical parameters[J].Progress in Physical Geography, 1998,22(4):449-476.
[10]Myneni RB, Maggion S, Iaquinta J,et al. Optical remote sensing of vegetation: Modeling, caveats, and algorithms [J].Remote Sensing of Environment, 1995,51(51):169-188.
[11]Lim K, Treitz P, Wulder M,et al. LIDAR remote sensing of forest structure[J].Progress in Physical Geography, 2003,27(1):88-106.[12]Peduzzi A, Wynne RH, Fox TR,et al. Estimating leaf area index in intensively managed pine plantations using airborne laser scanner data[J].Forest Ecology & Management, 2012,270(4):54-65.
[13]Solberg S. Mapping gap fraction, LAI and defoliation using various ALS penetration variables[J].International Journal of Remote Sensing, 2010,31(5):1227-1244.
[14]李文娟,赵传燕,别 强,等.基于机载激光雷达数据的森林结构参数反演[J].遥感技术与应用, 2015,30(5):917-924.
[15]Luo SZ, Wang C, Zhang GB,et al.Forest Leaf Area Index(LAI) Estimation Using Airborne Discrete-Return Lidar Data[J].Chinese Journal of Geophysics, 2013,56(3):233-242.
[16]Baltsavias EP. Airborne laser scanning: basic relations and formulas[J].Isprs Journal of Photogrammetry & Remote Sensing,1999, 54(2-3):199-214.
[17]赖旭东.机载激光雷达基础原理与应用[M].北京: 电子工业出版社,2010.
[18]Lerma JL. A new methodology to estimate the discrete-return point density on airborne lidar surveys[J].International Journal of Remote Sensing, 2014,35(4):1496-1510.
[19]邢艳秋,霍 达,尤号田,等.基于机载LiDAR单束激光穿透指数的白桦林LAI估测[J].应用生态学报, 2016, 27(11):3469-3478
[20]Kvalseth TO. Cautionary Note about R2[J].The American Statisti cian,1985,39(4):279-285.
[21]骆社周,王 成,张贵宾,等.机载激光雷达森林叶面积指数反演研究[J].地球物理学报, 2013,56(5):1467-1475.

