对课堂提问有效性的几点思考
曹 艳
(南京市第九初级中学,江苏 南京)
课堂提问是教师发挥主导作用,有效调节调控课堂教学活动的主要手段。有效提问能激发学生探究的兴趣、活跃学生的思维。下面就几个课例片段谈谈对课堂提问有效性的看法。
一、情境问题要能激发学生的探究欲望
苏霍姆斯林斯基说:“在人的心灵深处都有一种根深蒂固的需要,这就是希望自己是一个发现者、研究者、探究者,在儿童的精神世界里这种需求尤其强烈。”在初中数学课堂中,教师要对引入情境进行设计,将要解决的主要问题隐藏在情境中,通过熟悉的情境将学生的学习兴趣调动起来。例如,在圆的第一节课,引入定义时,设计如下四个问题:问题1:车轮为什么是圆的?为什么不是三角形或正方形或其他形状?问题2:能在地上滚动的有椭圆,为什么车轮不选椭圆?问题3:想象一下椭圆形车轮或正方形车轮的车子,人坐在上面是什么感觉?问题4:通过比较,你能说出圆具备什么特征?列举了学生生活中熟悉的问题,通过问题串形式,激发学生一步一步往下思考。对于车轮为什么是圆形的,学生对其中的原因并不很了解,更不能准确地表达出来。虽然是简单的问题,但是可以让学生在认知上产生冲突,意识到自己在数学方面还有很多不足,还有很多未知的知识有待去学习,激发了他们的探索欲和求知欲,同时激励他们更好地准备下一阶段的学习。
二、所提问题要具有逻辑性、连贯性
教师在课堂上提出具有逻辑性、连贯性的问题,可以让学生的思考向深处发展。孤立的设问只能让学生获得零乱的事实性知识,比如概念、性质等,对他们完整地思考问题没有帮助,影响了其逻辑思维的发展。提问应该有连贯性,问题与问题之间要有内在的变换和组合。教师设计的问题富有逻辑性并且有连续性,会使学生在学习的过程中不断建构网状的知识系统,形成重要的知识网络。比如在学习“线段的垂直平分线(1)”时,可以连续提出如下问题激发学生思考:
问题1:怎样画线段的垂直平分线?你有哪些方法?追问:你能用直尺和圆规作一条已知线段的垂直平分线?(视频演示作图过程)

问题2:为什么这样作出的直线CD就是AB的垂直平分线?提示:将问题转化成证明OA=OB,∠AOC=∠BOC=90°追问:怎样证明线段相等或角相等?
问题3:猜想:线段垂直平分线上的点到线段连段两端的距离有什么关系?提示:分别从线段垂直平分线上的点和垂直平分线外的点进行度量验证。追问:你能证明吗?(通过追问引导学生进行理论证明)本节课通过三个主要问题连续追问,启发学生如何去想怎么想,教给学生思考问题的方法,有利于学生的终身学习品质的培养。
三、提出的问题从学生已有知识入手,在思维的最近发展区处设问
课堂设计的问题,如果难度过大,让学生感到无从下手,容易挫伤学生思考的积极性;过于简单,没有思维深度。提出的问题过小、过易或一些浅层次记忆性知识的问题,学生不假思索就能对答如流,或是看起来回答的头头是道,并不能表明他们是真正理解了。在教学中不易体现教学难点重点,不能促进学生思维的发展。有一些课堂是表面上看上去热热闹闹,气氛很好,师生合作默契,但是没有任何的思维含量,反而会使学生养成不爱思考的不良学习习惯。我们提问一定要慎重,要从学生的实际出发,符合学生的知识经验和接受能力,问题设在学生的“最近发展区”,让学生跳一跳能够着。例如,初中一年级数学课中有关“负数”的教学,教师可以多举一些具体的、具有相反意义的量。如:可用温度计测温度的例子,在零摄氏度以上与在零摄氏度以下的时候,温度怎样表示,规定向东记为正,那么向西怎么记?得分记为正,失分怎么记?用他们身边熟悉的例子引入,产生一系列问题,他们渴望找到表示这些量的数,但是又有一定的困难,这样学生产生认知的矛盾,激起了学生强烈的求知欲,进而能很快掌握了负数的概念,并能运用其解决实际问题。
在探究合并同类型法则时设计了如下问题:问题1:试计算学校图书馆和教学区两块区域占地面积一共是多少?
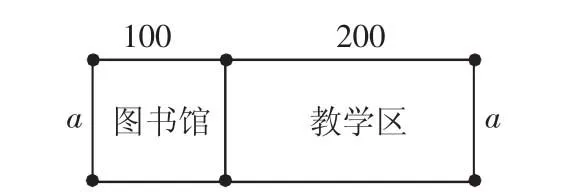
利用部分与整体的关系可以得到:100a+200a=(100+200)a=300a;
问题2:还有其他方法可以解释以上等式?引导学生从同类项角度结合乘法分配律考虑。此处从学生熟悉的图形入手,首先提出求图形的面积,问题容易,进一步设问是否有其他办法,层层递进,学生经过思考分析讨论归纳,自然生成合并同类项法则。
四、提出问题后要留足够时间让学生思考
在课堂上经常会遇到这样的现象:眼看着一堂课剩下时间不多了,但准备好的教学内容没有上完,教师为了节约时间,提问后立即让学生回答。学生没有足够时间思考,加上新知应用还不太熟练,结果问而不答或答非所问。心理学研究表明:在学习的过程中,对于一般的学生尤其是年龄较小的学生而言,在课堂上对老师提出的问题进行认真独立思考并不是一件非常容易的事。所以在恰当的时候保持一定时间的沉默是教师的最佳选择,有利于提高课堂教学效果。教师在提问后适当地等待可以给学生充分的时间进行比较全面的思考,答对或是答出意外惊喜的可能性就更大。对初中的学生而言,这样不仅增强了他们学习数学的自信心,而且有利于他们创造性思维的发展。有相关研究结果表明,教师提出一个问题之后,至少要等待三秒以上,再提学生回答效果才能更好。

