运用投影正弦图和点扩展函数法确定CT系统旋转中心＊

罗福婷，郑继明，张 亚，谢婷婷

（重庆邮电大学 理学院，重庆 400065）

计算机断层成像（ComputedTomography，CT）在医疗检测、无损检测和逆向工程中发挥着重大的作用，被视为20世纪影响人类发展的重大技术之一。安装CT系统时往往存在误差，会影响成像质量，因此，需要对安装好的CT系统进行参数标定，根据标定模板来确定CT系统旋转中心是首要问题。本文基于2017年“高教社杯”全国大学生数学建模竞赛A题[1]，讨论如何精确计算一种典型的二维CT系统旋转中心的问题。

CT系统旋转中心定位的方法有几何校正法、迭代校正法和投影正弦图重心法等[2]。几何校正法需已知精准的中心射线束的位置、焦距，这在工程应用中是不容易做到的，且会受计算效率的制约，实用性差；迭代校正法将旋转中心偏移转换为焦点问题，与手动调整原理相同，烦琐、精度低。张蔚等[3]根据CT系统投影正弦图的对称性、正弦性、参数信息等，提出投影图边缘法，先对投影正弦图进行分割，并二值化投影正弦图，将投影图分割为空气投影和工件投影两部分，求物体投影在各个方向的质心，最后将所有质心位置加权求均值。该方法能达到10-1像素级，是理想的旋转中心初始定位方法。为了进一步提高CT系统旋转中心定位的精度，本文提出了点扩展函数法。

考虑到点扩展函数仅能精确在1像素内的偏移量，首先分析了模板投影正弦图的特征，并对旋转中心进行初步定位，然后利用图像重建确定点扩展函数，从而较精确地确定出系统旋转中心。运用本文方法处理文献[1]中的数据，能够更精确地定位旋转中心。

1 预备知识

1.1 投影正弦图

在CT系统中，探测器-X射线源组合围绕模板旋转，一般为180°扫描，探测器接收到的信息即X射线经过模板衰减后的强度。衰减后的强度受厚度、空气、介质的影响，在不同的投影视角，不同位置的探测器采集到投影数据，即旋转角度θ与探测器t之间的关系为一条投影正弦曲线，即投影正弦图。投影正弦图中蕴含着非常多的信息，其对称性、正弦性、参数信息等都是不可忽略的重要内容。

1.2 点扩展函数与边缘响应函数

点扩展函数（pointspreadfunction，PSF）在CT系统重建图中表示空间中任意一点经过CT系统投影、重建之后在图像中的灰度强度分布[4-5]。边缘响应函数（edgeresponsefunction，ERF）是沿任意边缘法线方向的灰度分布曲线。在重建图像中，根据边缘的任意一点法线方向灰度分布来绘制曲线，取任意方向上不同半径的灰度值作曲线得边缘响应函数。物体的任意质点经过CT系统检测和图像重建之后，重建的图像并非一个质点，而是一个区域。获取实际点扩展函数的方法是，先获取图像的边缘响应函数，然后根据边缘响应函数计算图像的点扩展函数。

当旋转中心偏移量过大时，重建的图像模糊，由单边缘过渡到双边缘，边缘出现一层稳定灰度中间带，点扩展函数会出现双峰，无法判断极值与偏移量之间的关系。

1.3 Canny边缘提取

在确定旋转中心的过程中，需要通过Canny边缘提取对投影图、重建图进行处理。Canny边缘检测算法[6]首先用二维高斯函数的一阶导数对图像进行平滑。

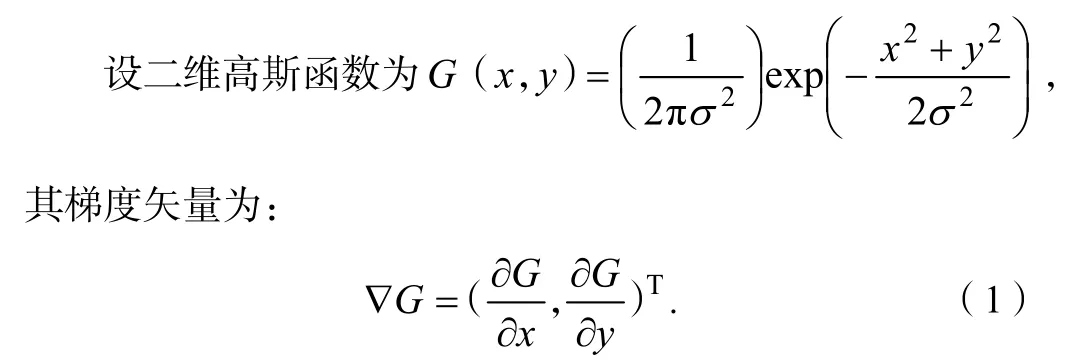
用分解的方法加快速度，把▽G的2个滤波卷积模板分解为2个一维行列滤波器，即：

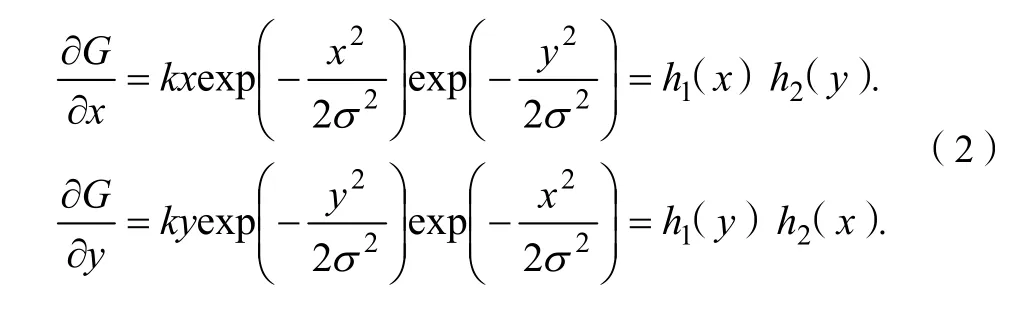
式（2）中：k为常数；σ为滤波器参数，它控制着平滑程度；h1（t）＝ktexp（-t2/2σ2），h2（t）＝exp（-t2/2σ2）.

对于σ小的滤波器，虽然定位精度高，但信噪比低；而σ大的情况则相反。经测试，本文高斯滤波器参数σ取0.27.

2 CT系统旋转中心定位算法

2.1 确定初始旋转中心

运用PSF仅能精确在1个像素内的偏移量[2]，对于偏移较远的旋转中心，需要进行初始定位。不同模板投影正弦图有不同特征，本文仅考虑在椭圆模板情形下运用投影正弦图确定初始旋转中心的问题。

对于N个探测器，从M个角度分别扫描得到投影图，对任一像素位置 E（i，j）（i∈[0，M]，j∈[0，N]）做如下处理：①对于投影图 E（i，j）（i∈[0，M]，j∈[0，N]），通过 Canny 边缘提取，得到边缘结果 T（i，j）（i∈[0，M]，j∈[0，N]）。②当旋转中心不发生偏移时，探测器中心与旋转中心对齐，所以，可通过旋转中心所在探测器位置来校正旋转中心。通过T（i，j）计算当前视角v下旋转中心偏移量△Pv，单位为像素。

当前视角v下旋转中心偏移量△Pv，即为在该视角下偏移量的投影，如图1所示，其中A为待定旋转中心，B为精确的CT系统旋转中心。

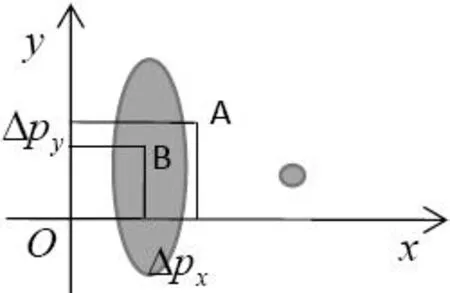
图1 旋转中心偏移量△Pv说明

椭圆模板的优势在于△Px、△Py对应的投影数据容易判断，探测器接收的数据最多，该列投影最长时对应偏移量△Py；探测器接收的数据最少，该列投影最短对应偏移量△Px，得到初始旋转中心A＝（△Px，△Py）。

2.2 偏移旋转中心计算及重建图像

通过初始旋转中心位置A或投影中心校正值d0校正旋转中心。设校正后旋转中心A1为p＝0的位置，PSF法仅能精确在1像素内的偏移量，所以，从p＝1开始依次偏移0.1像素到p＝1和p＝-1的位置，并依次运用直接反投影算法重建各个偏移量对应的CT图像。

2.3 基于Canny边缘提取确定REF和PSF

传统的Canny算法在2×2邻域内求有限差分来计算梯度幅值，该方法对噪声比较敏感。本文采用在3×3邻域内计算梯度幅值[7]，考虑了像素对角线方向，增加了计算像素偏导数的方向，改进了传统梯度幅值计算方法，使得边缘定位更准确。建立边缘响应函数的具体步骤是：①在Matlab软件中读取重建的图像，并通过rgb2gray命令得到灰度矩阵R＝（rij）n×n；②通过Canny边缘提取结果确定出椭圆模板中心M（a，b），其半径近似为r；③在模板中，以M（a，b）为起点，在水平正方向上分别取长度为r1和r2的2点，使得区间[r1，r2]跨越边缘（本文取区间长度为30）。于是，边缘响应函数为x（j）＝raj，j∈[r1，r2].

在重建图像中，对比度强、边缘清晰的图像边缘响应函数曲线的过渡带短；对比度低、模糊的图像，其边缘响应函数曲线的过渡带相对比较长，可以跨越几个像素甚至几十个像素。边缘响应函数的一阶导数为点扩展函数y（j）。在工程实际中，点扩展函数y（j）可通过差分格式计算，即y（j）＝Dx（j）＝x（j+1）-x（j），j∈[r1，r2].

2.4 CT系统旋转中心的确定

点扩展函数具有极大值，极值与偏移量间可以通过高斯函数拟合。当旋转中心不发生偏移，边缘响应函数陡峭变化，点扩展函数极值最大。通过拟合点扩展函数极值与偏移量，其高斯曲线峰值对应的偏移量即为旋转中心偏移量[2]。运用PSF精确定位旋转中心的步骤如下：①在不同偏移量下重建图像，得到边缘响应函数和点扩展函数；②求出不同偏移量下的点扩展函数极值；③拟合点扩展函数极值与偏移量之间的关系曲线G；④求出曲线G的峰值所对应的偏移量，即旋转中心偏移量。

由步骤①②③④分别得出x轴、y轴上偏移量△Px，△Py.如果以待确定旋转中心的位置为原点，对应的以重建图像中心为原点建立直角坐标系，则得到旋转中心坐标为（△Px，△Py）。

3 椭圆模板旋转中心的确定

下面以2017年“高教社杯”全国大学生数学建模竞赛A题给出的模板与相关数据为基础确定其旋转中心。

3.1 运用投影正弦图确定初始旋转中心

赛题模板如图2所示，根据接收信息画出其投影正弦图，如图3所示。

先通过投影图边缘法确定初始旋转中心，确定△Py＝22.5，△Px＝-33，得到初始旋转中心A＝（-33，22.5）（单位为像素，下同）。依据初始旋转中心A进行校正，校正后的旋转中心为A1，得到投影图、重建图如图4、图5所示。

3.2 偏移旋转中心及重建图像

水平方向为x方向，从校正后旋转中心A1开始（设此时偏移量p＝0），分别依次偏移0.1像素到p＝1和p＝-1的位置，运用直接反投影算法重建各个偏移量对应的CT图像。图6给出了x方向上部分偏移量时的重建图像。竖直方向（y方向）同理。

3.3 确定边缘响应函数

通过x（j）＝raj，j∈[r1，r2]得出不同偏移量下ERF函数。图7给出了x方向、y方向上部分ERF曲线，从中可以看出其曲线有差异。旋转中心偏移后越靠近系统精准的旋转中心，重建图像越清晰，其ERF函数曲线陡峭下降，如图7（a）中p＝-0.5，图7（b）中p＝0.1所示；反之，重建图像越模糊，其ERF函数曲线下降越平滑。

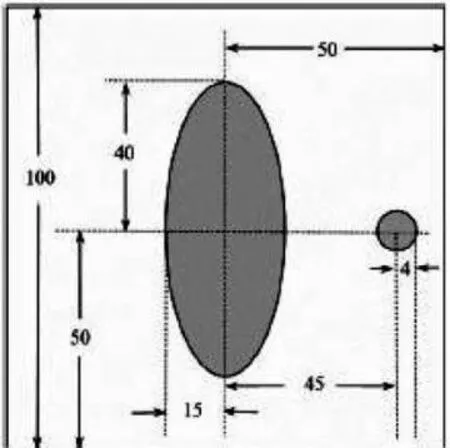
图2 赛题模板示意图

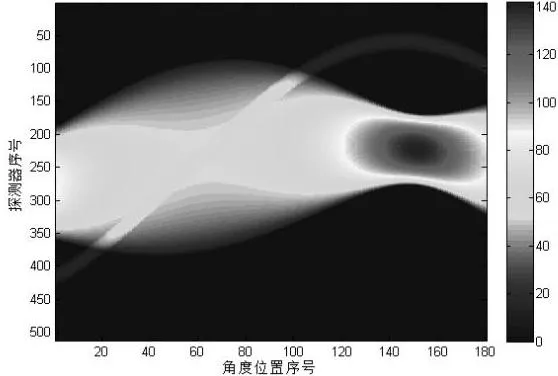
图3 赛题模板投影正弦图

图4 校正后的投影图

图5 校正后的重建图像

图6 x方向不同偏移量时重建图像

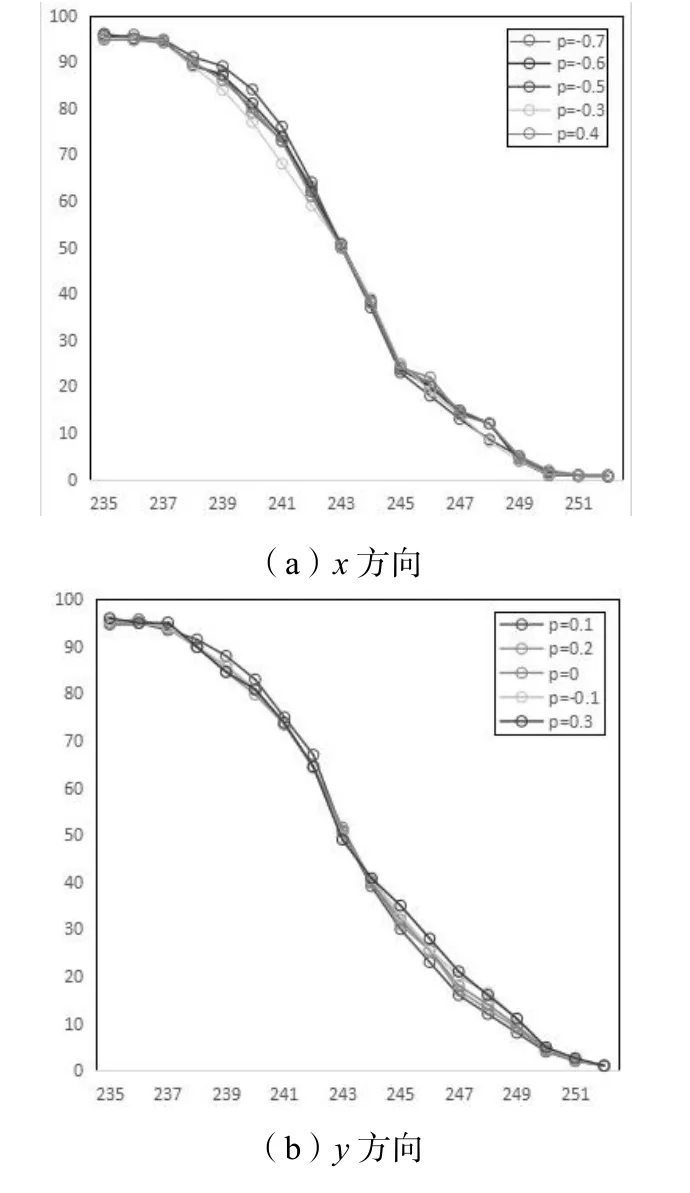
图7 各方向上不同偏移量对应的ERF函数曲线

3.4 确定点扩展函数

通过 y（j）＝Dx（j）＝x（j+1）-x（j），j∈[r1，r2]得出不同偏移量下PSF函数。图8给出x方向、y方向部分PSF曲线，从中可看出曲线有明显差异。在图8（a）中，从p＝-0.7到p＝-0.3，图8（b）中从p＝-0.1到p＝0.3，对应PSF极值先增大再减小，越接近系统精准的旋转中心，其PSF函数极值越大。

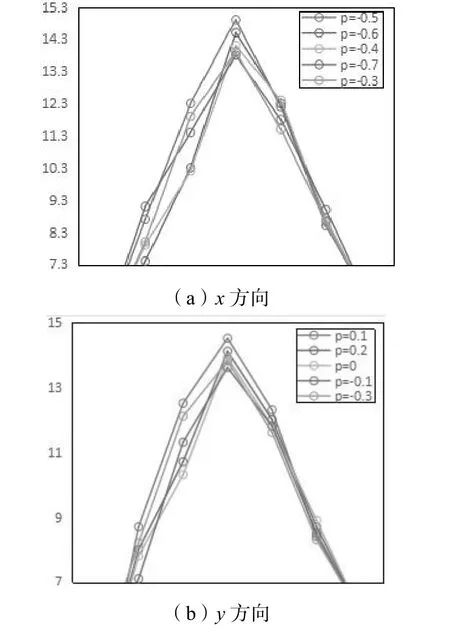
图8 各方向上不同偏移量对应的PSF曲线

3.5 根据旋转中心偏移量和PSF极值确定旋转中心

通过高斯函数拟合x方向、y方向上的偏移量与PSF函数极值的关系，得到图9.图9（a）峰值对应x轴上偏移量为-0.527 3，图9（b）峰值对应0.103 6，旋转中心A1＝（-0.527 3，0.103 6）；精确旋转中心为A+A1＝（-33.527 3，22.603 6），单位为像素。

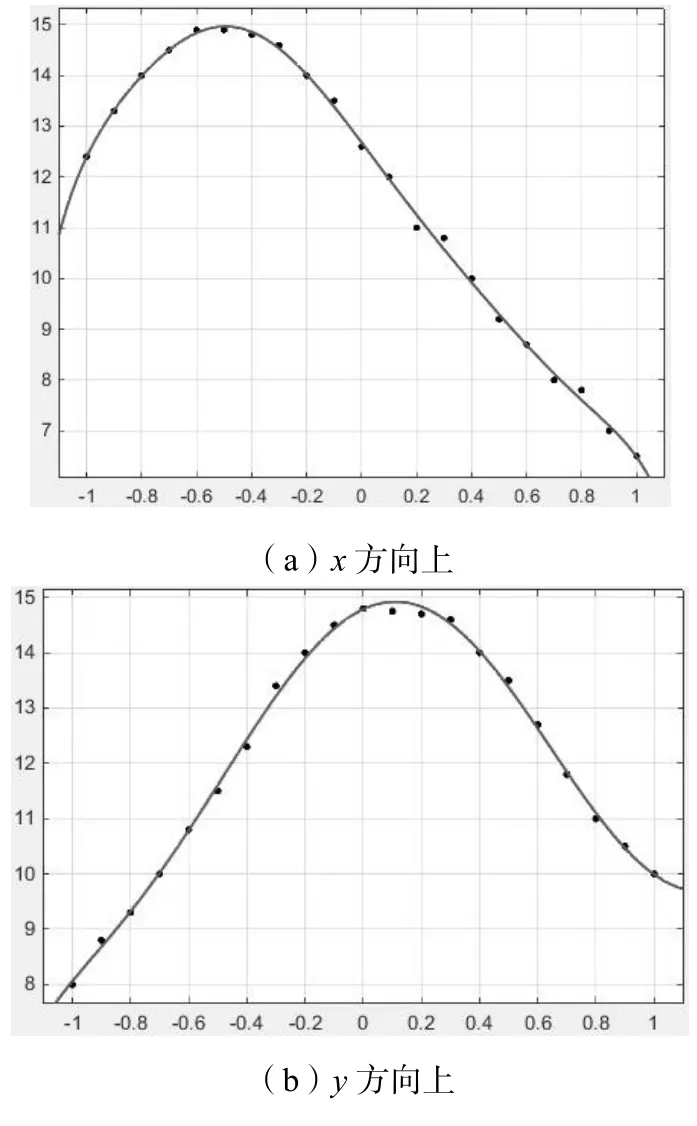
图9 偏移量与PSF函数极值拟合

由PSF法精确后校正旋转中心，再扫描模板并重建图像。图10由于旋转中心偏移比较远，未校正重建图像十分模糊，边缘伪影、阴影严重；图11初始校正后阴影减小，但边缘依然不够光滑；图12通过PSF精确定位并校正后，重建图像明显清晰，边缘光滑。

4 结束语

安装CT系统会导致旋转中心偏移，其误差会使重建图像出现伪影，降低成像质量。系统旋转中心位置定位越准确，重建图像质量越好。本文先运用投影正弦图法进行初始定位，再运用PSF法进一步精确定位了CT系统的旋转中心。在未来的研究中，将用更具有特征的模板来标定旋转中心，例如均质圆盘模板，其可以降低噪声影响，便于分析和观察。

图12 PSF法校正

图10 未校正

图11 初始校正

［1］全国大学生数学建模竞赛组委会.2017年竞赛A题［EB/OL］.［引用日期不详］.http://www.mcm.edu.cn.

［2］刘明进.工业CT系统旋转中心定位方法研究［D］.重庆：重庆大学，2014.

［3］张蔚，罗守华，陈功.Micro-CT系统中对投影图像旋转中心的校正［J］.医疗卫生装备，2009，30（3）：4-6.

［4］孙怡，朱佩平，于健，等.X射线衍射增强成像中吸收、折射以及散射衬度的计算层析［J］.光学学报，2007，27（4）：749-754.

［5］张晓瑞.基于Radon变换的滤波反投影重建算法研究［J］.电脑知识与技术，2016，12（27）：259-261.

［6］王植，贺赛先.一种基于Canny理论的自适应边缘检测方法［J］.中国图象图形学报，2004，9（8）：957-962.

［7］文章，张欣，周昌顺，等.一种基于Canny的边缘检测改进算法［J］.通信技术，2017，50（10）：2236-2240.

［8］孟凡勇，王维，李静海.利用正弦图自动校正CT投影中心［G］//全国射线数字成像与CT新技术研讨会论文集.绵阳：中国体视学学会，2008：265-271.