基于GNSS的前视双基SAR点扩散函数产生算法＊

刘文超，曾张帆，史智明，周艳玲，潘永才

（湖北大学 计算机与信息工程学院，湖北，武汉 430062）

1 引言

前视雷达成像技术在飞机自主导航和着陆、战地战况监测等领域有着广泛的应用，越来越引起研究人员的关注。相比传统的单基雷达，双基前视合成孔径雷达（Bistatic Forward Looking SAR，BFLSAR）提供了二维分辨可行性，为二维成像奠定了理论基础。德国、英国、中国等世界主要雷达大国就BFLSAR雷达系统的二维分辨特性、同步技术、成像技术等一系列雷达关键技术进行了深入的研究[1-3]。

基于GNSS的双基合成孔径雷达系统（GNSS-BSAR）是一类特殊的被动式双基合成孔径雷达系统，由英国伯明翰大学的Mikhail Cherniakov[4]在2003年首先提出。该雷达系统以GNSS导航卫星作为发射源，接收机能够放置在另一颗卫星、飞机、汽车上，或是静止放置在地面，对目标区域进行观察、成像、测高、形变监测等。该系统具有安全性好、造价低廉、稳定性好、卫星数量多、重访周期短、系统配置灵活等技术优势，弥补了传统双基合成孔径雷达的不足。然而，由于其采用非合作卫星，其接收信号微弱、时频同步复杂度高、二维空变性等一系列问题一直以来都成为了该体制雷达研究领域的重难点。

基于GNSS的双基前视合成孔径雷达（GNSS-BFLSAR）是结合上述传统的双基前视雷达和GNSS-BSAR系统，在此基础上派生形成的新体制雷达系统。该雷达系统采用GNSS卫星作为发射源，而接收机部署在飞机上，飞机沿直线飞行，成像目标在飞机前方。GNSS-BFLSAR系统拥有部署成本低、安全性好等技术优势，在自主着陆、自主导航、战场地形获取等方面有着广阔的应用前景。GNSS-BFLSAR系统示意图如图1所示。本文对基于GNSS的双基前视合成孔径雷达点扩散函数的产生方法进行了研究。论文结构如下：第2节给出了GNSS-BFLSAR的回波模型；第3节推导出GNSS-BFLSAR点目标回波二维频谱；第4节介绍了点扩散函数的产生方法；第5节对二维频谱进行仿真，并获得点目标扩散函数（Point Spread Function，PSF）。最后对本文进行了总结，并提出了未来的研究方向。

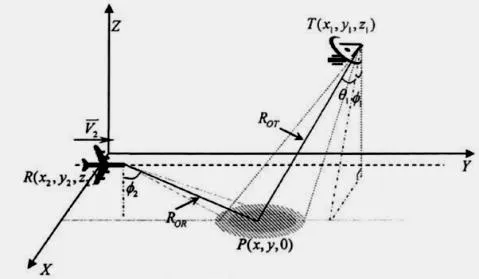
图1 GNSS-BFLSAR系统示意图

2 GNSS-BFLSAR回波信号模型

在GNSS-BFLSAR雷达系统中，辐射源发射的信号为单频连续波信号，经过收发站同步、去载频等操作后，回波信号为：

式（1）中：τ为快时间；η为慢时间；σ为地面反射系数；s[t-τ（η）]为回波信号的包络；λ为载波波长。

R（η）为双基SAR的距离历程，包括辐射源到目标的距离和目标反射到接收机的距离：

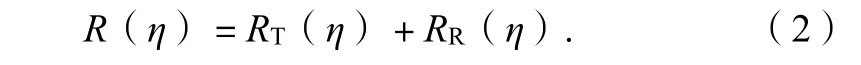
式（2）中：RT为辐射源到目标的距离。

式（3）（4）中：Rrc和θrc是零时刻接收机到点目标的距离和斜角；Rtc和θtc是零时刻发射机到点目标的距离和斜角；vt和vr是发射机平台和接收机平台的速度。

3 GNSS-BFLSAR二维频谱

本节采用POSP方法对GNSS-BFLSAR回波信号进行时频变换，获得其二维频谱，具体步骤如下。

3.1 GNSS-BFLSAR距离向傅里叶变换

对GNSS-BFLSAR回波信号（公式（1））进行距离向傅里叶变换，得到回波信号在距离向的频域表达式：

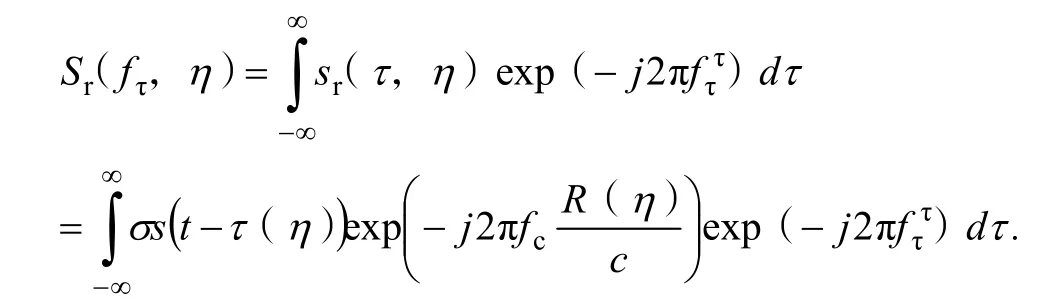
3.2 GNSS-BFLSAR方位向傅里叶变换

对距离向傅里叶变换后的GNSS-BFLSAR回波信号，进行方位向傅里叶变换，得到其二维频谱：

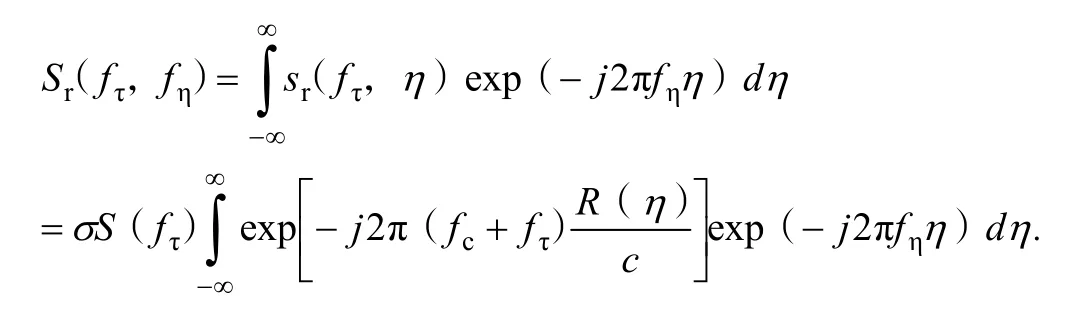
其中，fη为方位向频率。

采用POSP方法，得到GNSS-BFLSAR回波二维频谱：Sr（fτ，fη）＝σS（fτ，fη）exp[-jφ（fτ，fη）].其中，

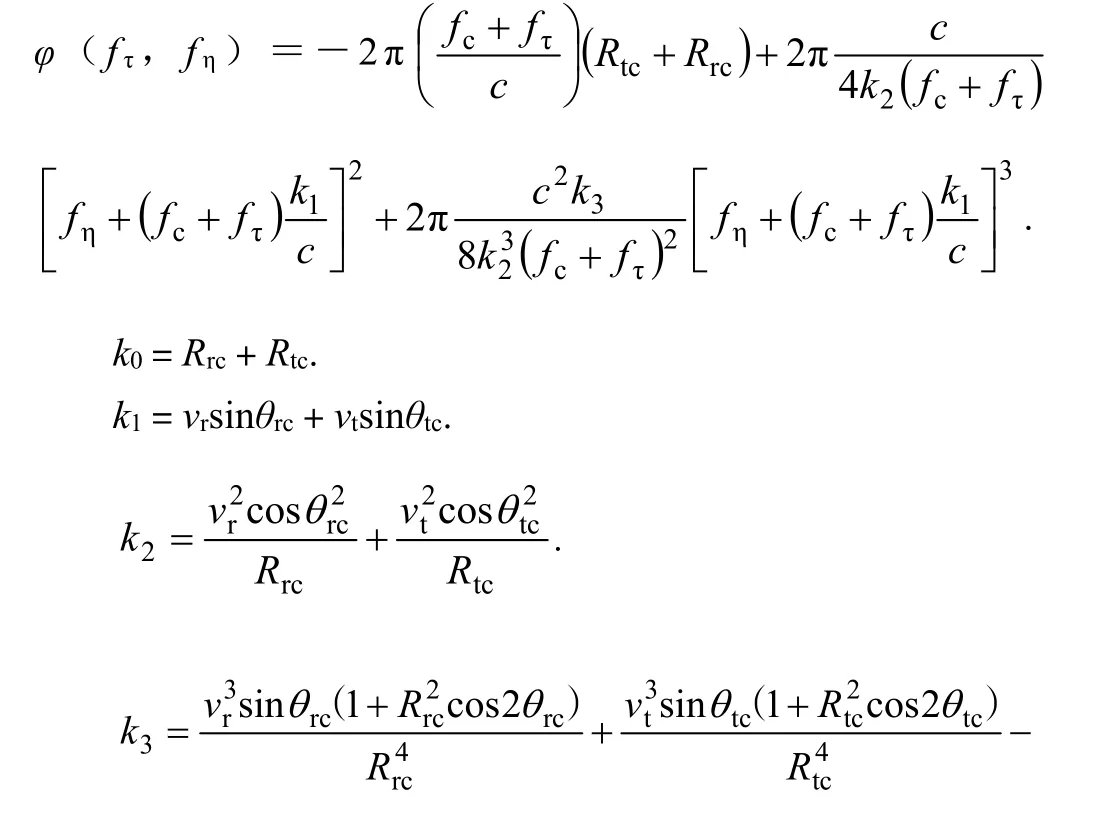
4 GNSS-BFLSAR点扩散函数产生方法

GNSS-BFLSAR点扩散函数产生方法依次包含距离向脉冲压缩、距离徙动校正、高阶相位校正以及方位向脉冲压缩，具体步骤如下。

4.1 距离向脉冲压缩

距离向脉冲压缩由GNSS-BFLSAR二维频谱与脉冲压缩参考信号卷积运算实现，脉冲压缩参考信号表达式为：

4.2 距离徙动校正

距离向脉冲压缩由GNSS-BFLSAR二维频谱与脉冲压缩参考信号卷积运算实现，距离徙动校正参考信号表达式为：

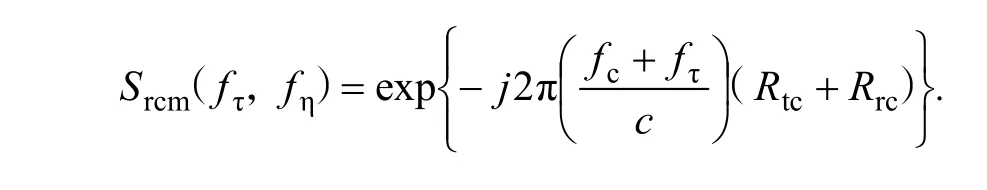
距离徙动校正后的信号表达式为：

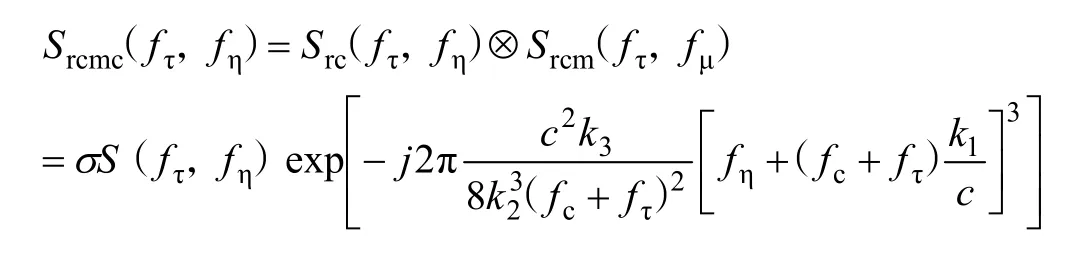
4.3 高阶相位校正

距离向脉冲压缩由GNSS-BFLSAR二维频谱与脉冲压缩参考信号卷积运算实现，高阶相位校正参考信号表达式为：

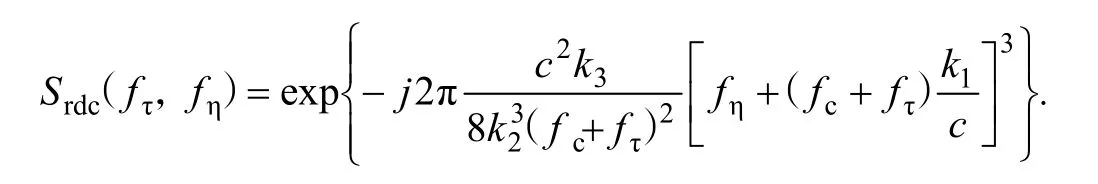
高阶相位校正后的信号表达式为：

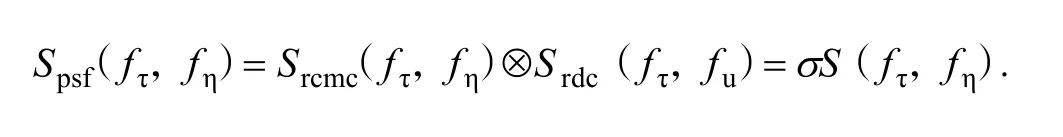
5 点目标仿真

本节根据上述提供的对GNSS-BFLSAR雷达系统回波二维频谱的理论推导进行了点目标仿真，仿真参数如表1所示。点目标仿真结果如图2所示。点目标在东向和北向的切面图如图3所示。

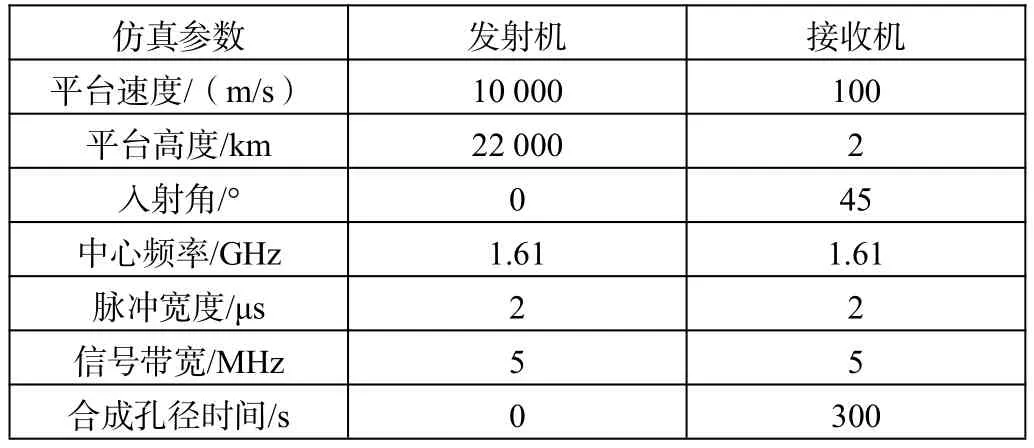
表1 GNSS-BFLSAR雷达系统点目标仿真参数

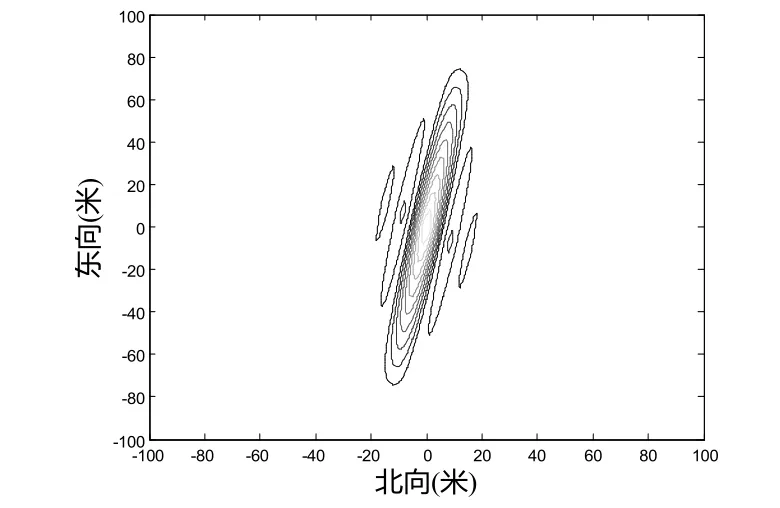
图2 GNSS-BFLSAR雷达系统点目标仿真结果

图3 点目标在东向和北向的切面图

由图2和图3可见，在进行POSP之前进行双基斜距历程泰勒展开，保留三阶项后的聚焦性能接近理论值，因此可以实现理想聚焦。距离向、方位向聚焦性能参数，即峰值旁瓣比（PSLR）、积分旁瓣比（ISLR）和脉冲宽度（IRW）如表2和表3所示。需要注明的是，与传统的以Chirp信号作为工作信号的雷达不同，本文研究的雷达系统的工作信号为伪随机码的BPSK信号，该信号的自相关函数特性符合图3（a）和表3.表2和表3中的聚焦性能值表明，本文提供的二维频谱解析式有着较高的准确性。

表2 北向聚焦性能

表3 东向聚焦性能

6 结论

本文研究了基于GNSS的双基前视SAR雷达系统点扩散函数产生方法。采用二维傅里叶变换和POSP原理对回波信号进行了时频变换，并使用Taylor展开对距离向频谱和方位向频谱进行了解耦，获得了二维频谱近似解析式。我们发现，GNSS-BFLSAR雷达系统在二维频域同时具有距离向走动和方位向走动的特性，且距离向走动和方位向走动的幅度均与接收机平台到目标的距离有关。最后采用Matlab对GNSS-BFLSAR系统的点目标进行了仿真，仿真结果验证了文中对该系统二维频谱理论推导的准确性。接下来我们将在不同的几何构型下对GNSS-BFLSAR雷达系统进行理论分析与系统仿真，对其分辨率等雷达性能进行研究。

［1］Thomas E.，Ingo W.，J Klare，et al.Bistatic Forward-Looking SAR：Results of Spaceborne-Airborne Experiment.IEEE Geoscience and Remote Sensing Letters，2011，8（4）：765-768.

［2］Xiaolan Q.，Donghui H.，Chibiao D.Some Relections on Bistatic SAR of Forward-Looking Configuration.IEEE Geoscience and Remote Sensing Letters，2008，5（4）：735-739.

［3］Wenchao L.，Yulin H.，J Huang，et al.An Improved Radon-Transform-Based Scheme of Doppler Centroid Estimation forBistatic Forward-Looking SAR.IEEE Geoscience and Remote Sensing Letters，2011，8（2）：379-383.

［4］Mikhail Cherniakov，MAntoniou，R Saini.Image formation algorithms for space-surface bistatic SAR.IEEE Transactions on Geoscience&Remote Sensing，2007，45（11）：3359-3371.

［5］T Zeng，T Zhang，WM Tian，et al.A novel subsidence monitoring technique based on space-surface bistatic differential interferometry using GNSS as transmitters.Science China Information Sciences，2015，58（6）：1-16.