经典电偶极子在交变电场下的运动

王荣秀，王 波

(1.重庆工商大学， 重庆 400067； 2.重庆理工大学， 重庆 400054)

电偶极子模型是一个非常重要的基础模型，在涉及电磁场与物质的相互作用、电磁波的发射和吸收、分子原子的相互作用理论等领域有着十分广泛的应用[1-2]。例如，利用偶极子模型用于研究近场光学显微镜和样品的相互作用等问题[3-5]。在研究电介质及其与电场的相互作用时，也往往采用电偶极子模型，如电介质的极化[6]、铁电体材料中电畴分布与转向等问题[7-8]。在已有的文献中有一些关于电偶极子的研究报道，如偶极子激发的电场和磁场分布[9]、偶极子与偶极子的相互作用[3]、偶极子在静场中的运动[10]等。这些研究大都将外场看成是静场，或将偶极子看成是静止或匀速运动，没有讨论偶极子中正负电荷粒子由于加速运动而激发的电磁场对其本身运动的影响，同时对偶极子在外场中的转向问题也研究不多。

详细研究偶极子的运动规律需要应用量子场论的基本理论，但在低速经典的近似条件下也可以得出一些具有普遍意义的结论[1-2,11]。本文针对交变电场中的电偶极子的运动进行研究，建立了正负粒子运动方程，讨论了偶极子的运动特点及在静场/准静场情形下偶极子的转向运动。

1 电偶极子及其相互作用

1.1 低速运动的带电粒子

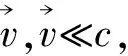
(1)

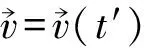
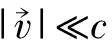
此即为单位时间内粒子辐射出去的能量。

(2)

在一般情况下，式(2)并不是严格成立的，因为没有考虑粒子加速运动时，其附近的电磁场也在变化，因此式(2)不代表瞬时关系，而是一种时间的平均效应。假如粒子作准周期运动，在1个周期之后，粒子附近的场回到原状态，则阻尼力所作的负功等于辐射出的能量，由此对式(2)进行1个周期的积分是可行的。设周期为T，则

当粒子运动1个周期后，速度与加速度回到原值，第1项积分为0。就平均效应来看，取

(3)

(4)

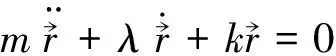
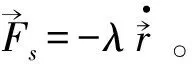
1.2 电偶极子模型

由式(1)(2)可知：在无外力或外场作用时，偶极子正负粒子在其平衡位置附近振动，由于具有速度与加速度，还会受到电磁阻尼与对偶粒子激发的电磁场的作用。

2 电偶极子在交变电场下的运动

2.1 偶极子运动方程

(5)

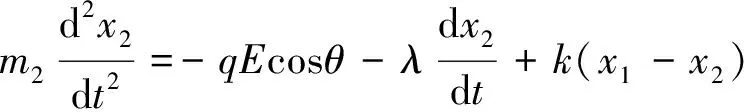
(6)

(7)

(8)

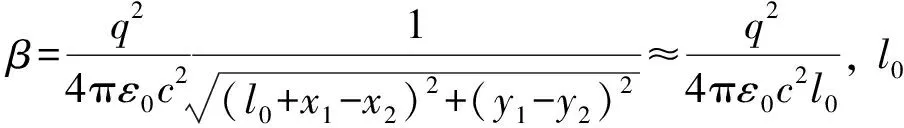
2.2 方程求解

对方程(5)～(8)求解时讨论两种较典型的情况：m1=m2及m1>>m2。

当m1=m2=m时，令：Xn=x1+x2，Yn=x1-x2，Xt=y1+y2、Yt=y1-y2，则：

(9)

(10)

(11)

(12)

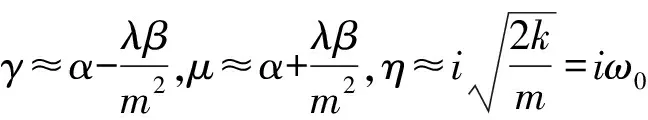
其中c3、c4、d3、d4也是常数。

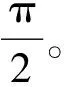
2.3 偶极子的转向

偶极子转向是由于正负粒子相对于平衡位置所产生的位移，但主要取决于垂向位移。设θ的增量为Δθ，正负粒子之间的距离近似为l0，则有：

(13)

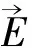
(14)

负号表示角θ沿减小方向变化。

由于偶极子转向运动在静场或准静场条件下才是明显的，不妨假定ω≈0。此时式(14)与单摆运动方程相同，表明偶极子以电场方向为轴向作摆动。如不考虑其他外力的作用，衰减项的存在使得摆动的幅度慢慢变小，最后偶极子取向沿外场方向，正负粒子在其平衡位置附近作小幅振荡。当θ很小时，式(14)就是简谐振动方程。

当ω≈0时，由式(14)可解得

(15)

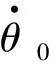
2.4 m1>>m2时的偶极子运动

当m1>>m2时，m1位置近似为质心，其位移和速度很小，可忽略不计。此时重要的是m2相对于m1的运动，因此只考虑m2的运动方程。取x1=y1=0，并记m2=m，由式(6)(8)可得：

(16)

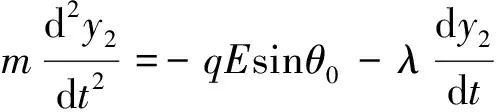
(17)

可以看出，除常系数2外，式(16)与式(10)相同，式(17)与式(12)相同，其解分别为：

此时偶极子的运动特点与本文3.2和3.3节所述类似，本文不再重复分析。

3 结束语

在外加交变电场作用下，除由粒子间弹性恢复力引起的谐振外，电偶极子的主要运动是随外场频率作受迫振动。同时，由于其正负粒子运动所激发的电磁场，还会受到自身的电磁阻尼及对偶粒子横向电场的作用。偶极子的质心可以近似地看成静止或作匀速运动，正负粒子沿轴向及垂直方向的运动具有对称性。粒子沿轴向的运动是受迫带阻尼的谐振运动，当外场频率接近电偶极子的固有频率时，发生受迫共振，而沿垂向则是受迫阻尼振动。二者与外场相比均存在相位相差90度的弱小分量。在外场频率较高时，偶极子主要表现为在其平衡位置附近的振动，电偶极矩与外场方向的夹角变化较小，不出现明显的转向运动；在静场或准静场条件下，电偶极子发生转向运动，其运动形态类似于单摆绕轴线的周期运动，其角速度大小依赖于偶极子初始状态，并与电偶极矩与外场夹角有关。

[1] 李元杰.电动力学[M].北京:机械工业出版社，2014.

[2] DAVID J G.Introduction to Electrodynamics[M].北京:机械工业出版社，2016.

[3] 邹文栋，王立法.偶极子-偶极子库仑相互作用能及其电动力学特性[J].南昌航空大学学报，2008，22(4):32-35.

[4] MOGILATOV V S，ZOLBINSKY A V.A circular electric dipole:a transmitter for TEM surveys[J].Russian Geology and Geophysics，2014，55(1):1340- 1346.

[5] 吴才章，叶梅，叶虎年.扫描近场光学显微镜的光耦合偶极子模型[J].光子学报，2005，34(10):1546- 1549.

[6] 周艳丽，熊畅.电介质极化现象的微观机制讨论[J].大学物理，2015，34(6):9-12.

[7] CHEN Y，XIE S X，WANG H M，et al.Dielectric abnormality and ferroelectric asymmetry in W/Cr co-doped Bi4Ti3O12ceramics based on the effect of defect dipoles[J].Journal of Alloys and Compunds，2017，696:746-753.

[8] POZZI G，BELEGGIA M，KASAMA T，et al.Interferometric methods for mapping static electric and magnetic fields[J].Comptes rendus physique，2014，15(2):126-139.

[9] 晏光辉，刘志环，姜东光.匀速运动的电偶极子的电场与磁场分布[J].物理与工程，2006，3(5):22-26.

[10] 任恒峰，王清亮，连润明，等.外电场下电偶极子运动规律研究[J].商丘师范学院学报，2012，28(9):38-41.

[11] 高守恩，杨建宋.量子力学[M].北京:清华大学出版社，2014.

[12] 黄昆，韩汝琦.固体物理学[M].北京:高等教育出版社，2010.