螺栓连接薄壁柱壳结构固有特性分析*

张文胜 徐世俊 孟春晓 李坤 马辉† 秦朝烨

(1.上海航天设备制造总厂有限公司, 上海 200245) (2.东北大学 机械工程与自动化学院, 沈阳 110819) (3.清华大学 机械工程系, 北京 100084)

引言

机械装配中的连接形式种类繁多,有螺栓连接、胶结、焊接、销连接等形式[1],且连接结构的装配性能及其稳定性是目前国内外研究的热点之一,因此如何正确处理零部件之间的连接关系或装配关系是一个十分重要的技术问题[2].目前,螺栓连接作为机载设备设计制造中一种常用的连接方式,因其具有加工方便、可操作性好、承载能力强、便于装配、可靠性高、便于拆卸等优点[3],被广泛应用于转子系统的连接结构中.

在工程实际中,为改善螺栓连接结构的刚度、提高连接精度、防止松动的发生,多数情况下需要对装配螺栓进行适当预紧[4,5],并且预紧力和连接面的接触状态对连接结构的固有特性影响较大.为了研究包含螺栓连接结构的复杂机械力学特性[6],国内外很多学者对螺栓连接结构的建模进行了大量的研究和分析.

Maio等[7]将螺栓连接简化为刚性连接,但这种分析方法很难考虑连接件间的接触特性,会导致整个连接结构的振动模态计算结果偏大.Kim等[8]考虑了螺栓预紧效应和法兰之间的接触行为,采用预应力模态法分析螺栓连接结构,该方法具有较高的准确性.在有限元方法的基础上,Marc等[9]基于实验测试结果,采用线性弹簧、非线性弹簧单元、阻尼单元对螺栓连接结构进行了建模.姚星宇等[10,11]则将有限元和解析相结合,针对螺栓连接薄壁筒结构,推导了连接刚度理论表达式,进而采用薄层单元来模拟螺栓连接界面,探究了螺栓预紧力对结构固有特性的影响.文献[12,13]认为螺栓连接结构的预紧力夹紧区域为类圆锥形,并提出将预紧力夹紧区域进行粘接可应用于螺栓建模中,但其仅适用于大预紧力情况.工程实际中,由于预紧力的施加,螺栓连接结构界面接触摩擦问题不可避免[14-17].因此,针对螺栓连接薄壁结构应考虑预紧力对其固有特性的影响.文献[18,19]分析了螺栓连接结构在不同预紧力下的固有特性,结果表明,预紧力对系统的固有特性影响较大,且预紧力越大,系统的固有频率越高.此外,在对螺栓连接结构的固有特性进行研究时,Wei等[20]研究了螺栓数目及螺栓位置对系统固有频率的影响,研究结果表明随着螺栓数目的增加,系统固有频率不断增加,且螺栓间距越大,螺栓数量对固有频率的影响越明显.

根据上述文献可知,在螺栓连接结构方面,对于螺栓连接结构的建模方法的研究比较系统,对于连接结构界面接触特性的研究内容较为丰富,研究模型已经从集中参数模型逐渐发展到三维实体模型,研究内容已经从线性范围逐步扩展非线性范围.然而,在螺栓连接的薄壁柱壳结构方面,较少有文献考虑转速和预紧力联合作用下对系统固有特性的的影响.基于这一点,本文首先基于ANSYS仿真软件,建立了典型的螺栓连接薄壁柱壳结构；其次通过仿真与实验模态结果对比,验证了基于接触的预应力模态法求解系统固有频率的有效性；最后考虑离心刚化、旋转软化和科式力效应,探究了螺栓预紧力和系统转速对螺栓连接薄壁筒结构的固有特性的影响.

1 有限元模型及模型验证

1.1 接触力学模型

在螺栓连接结构中,接触区域的接触状态与载荷、材料、边界条件等因素相关,且对结构动力特性影响较大.因此,需要采用合理的接触算法来描述螺栓连接件间的接触问题.常见的接触算法包括罚函数法、拉格朗日乘子法和增广的拉格朗日乘子法[21].罚函数法在求解复杂接触问题时容易导致收敛困难,拉格朗日乘子法则会导致迭代次数的增加,而增广拉格朗日乘子法通过将罚函数中的罚项加入到拉格朗日乘子法中,提高了计算精度,改善了收敛性.因此,本文采用增广拉格朗日乘子法来处理连接件间的接触问题.

基于Hamilton原理得到系统的能量泛函表达式如下：

(1)

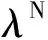
基于有限元法的基本理论,将式(1)中进行变分和离散化处理后,可得到含接触问题的系统自由振动微分方程如下：

(2)

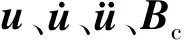
值得说明的是,本文仅进行含螺栓连接的旋转薄壁柱壳结构的固有特性分析,因此,式(2)可进一步简化为如下表达式：

(3)

此外,由于系统涉及到接触问题,因此,接触点对间还应满足接触界面的非穿透和库伦摩擦条件：

(3)

‖tTi‖≤μλNi(α)

(4)

其中,上标i表示第i个接触对,q表示接触对数,λNi(α)是拉格朗日乘子；tTi表示界面摩擦力；gNi表示第i个接触对的正常间隙；μ表示摩擦系数.

相关求解含接触的系统刚度矩阵K的计算流程图如图1所示.基于所获得的K和M,便可求得预应力状态下系统的固有频率和振型.

1.2 有限元模型建立与验证

图2为螺栓连接薄壁柱壳结构示意图,薄壁柱壳结构几何参数如下：左盘半径为R=150 mm,长为L1=20 mm,右盘直径为R=150 mm,长为L2=25 mm,左右筒结构相同,内半径R1=117 mm,外半径R2=120 mm,长为L=160 mm,法兰螺栓孔中心圆半径R3=126 mm,外圆半径R4=132 mm,法兰厚h=3 mm,螺栓孔直径d=5 mm.其中,两薄壁柱壳结构通过24个M4标准螺栓、螺母进行连接.

真实试验件结构中增加了厚度(H=25 mm)和外径(D=240 mm)相同的两个法兰盖板,其中法兰盖板和两筒盖通过24个M20螺栓完全拧紧,因此,在建立有限元模型时,忽略了法兰盖板和两筒盖之间的接触非线性,将法兰盖板和筒盖进行一体化建模.建模时,基于ANSYS软件,采用实体单元(Solid185单元)建立螺栓连接的薄壁柱壳精细有限元模型,其中材料参数设置如下：弹性模量210 GPa,泊松比0.3,密度7800 kg/m3；接触设置如下：采用接触单元Targe170和Conta174模拟螺栓头与左筒、螺母与右筒、左右筒之间的接触与摩擦,摩擦系数设置为0.15；采用预紧力单元Prets179模拟螺栓预紧力,通过查询机械设计手册确定螺栓预紧力大小为800 N.

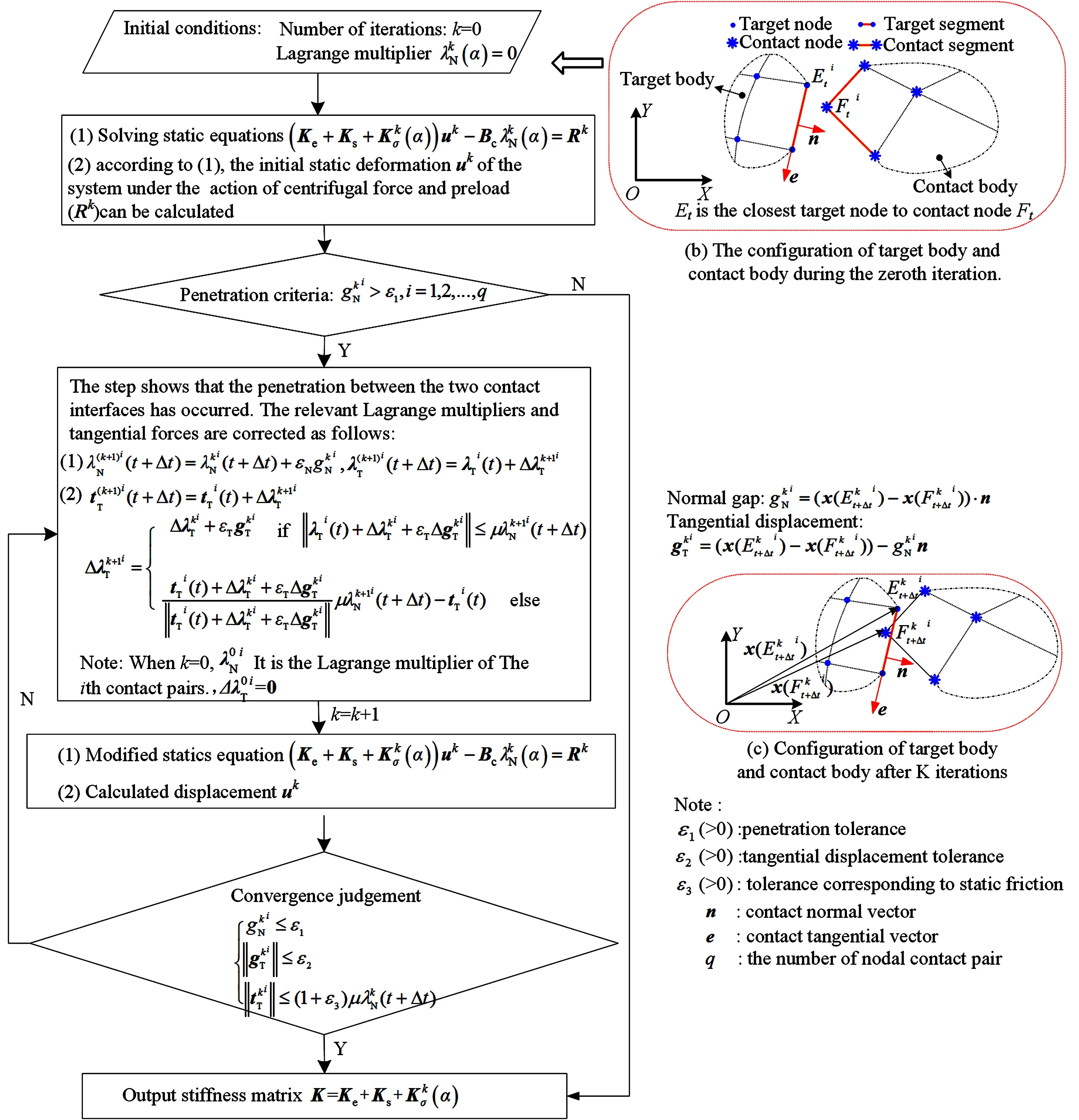
图1 基于接触动力学的接触求解流程图Fig.1 Flow chart of solution based on contact dynamics

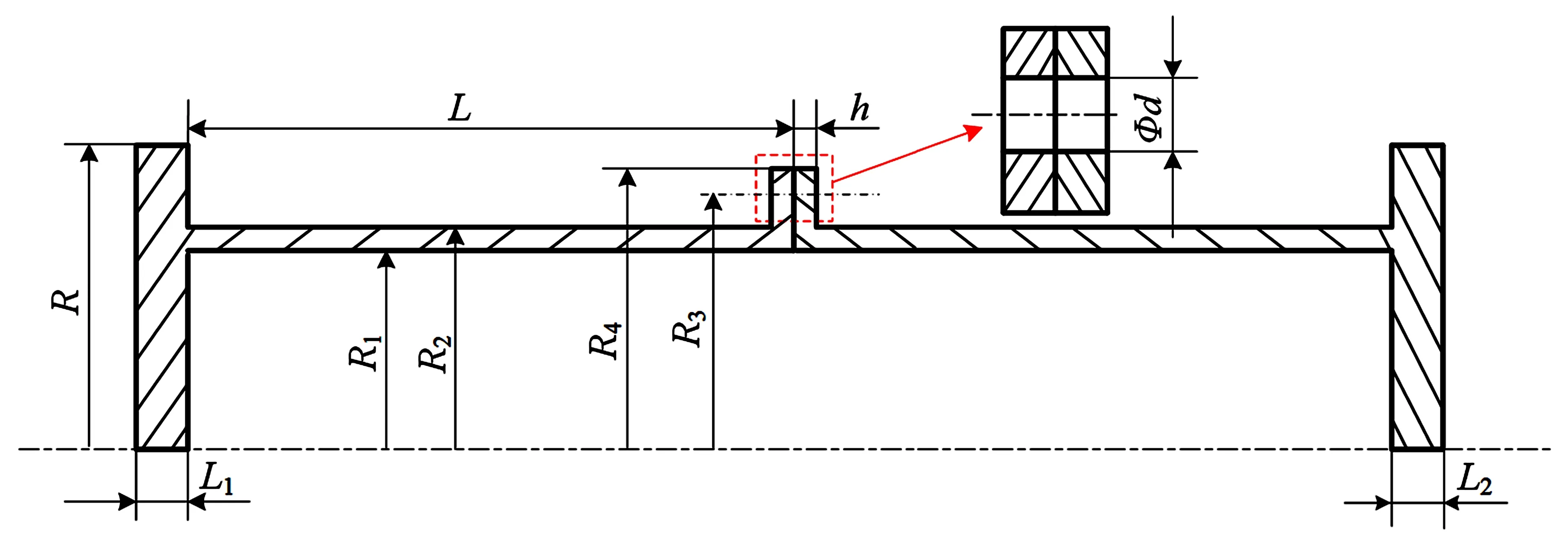
图2 螺栓连接薄壁柱壳结构示意图Fig.2 Schematic diagram of bolted thin-walled cylindrical shells

图3 试验件和分析系统Fig.3 Test piece and analysis system

为了验证所建模型的正确性,本节对该螺栓连接的薄壁柱壳结构进行实验验证.实验过程中采用LMS SCADASⅢ型振动测量系统及其配套的TestLab软件进行数据的测试和分析,采用PCB公司的力锤进行敲击,扭矩扳手施加预紧力和三向加速度传感器进行数据采集.具体的测试系统、实验件、测试工具和辅助设备,如图3所示.

实验件安放在未充满的轮胎上面以此来模拟自由边界条件.螺栓连接的薄壁柱壳结构共分布24个测试点(见图4),在上下筒连接处中间圆周方向均布8个测点,在上下筒圆周方向各均布8个测点,三向加速度传感器安装在中间连接处和上筒面.测量时,仪器的设定频率测量范围为0～4096 Hz,采用锤击法测量螺栓连接薄壁柱壳结构的固有频率及振型图.

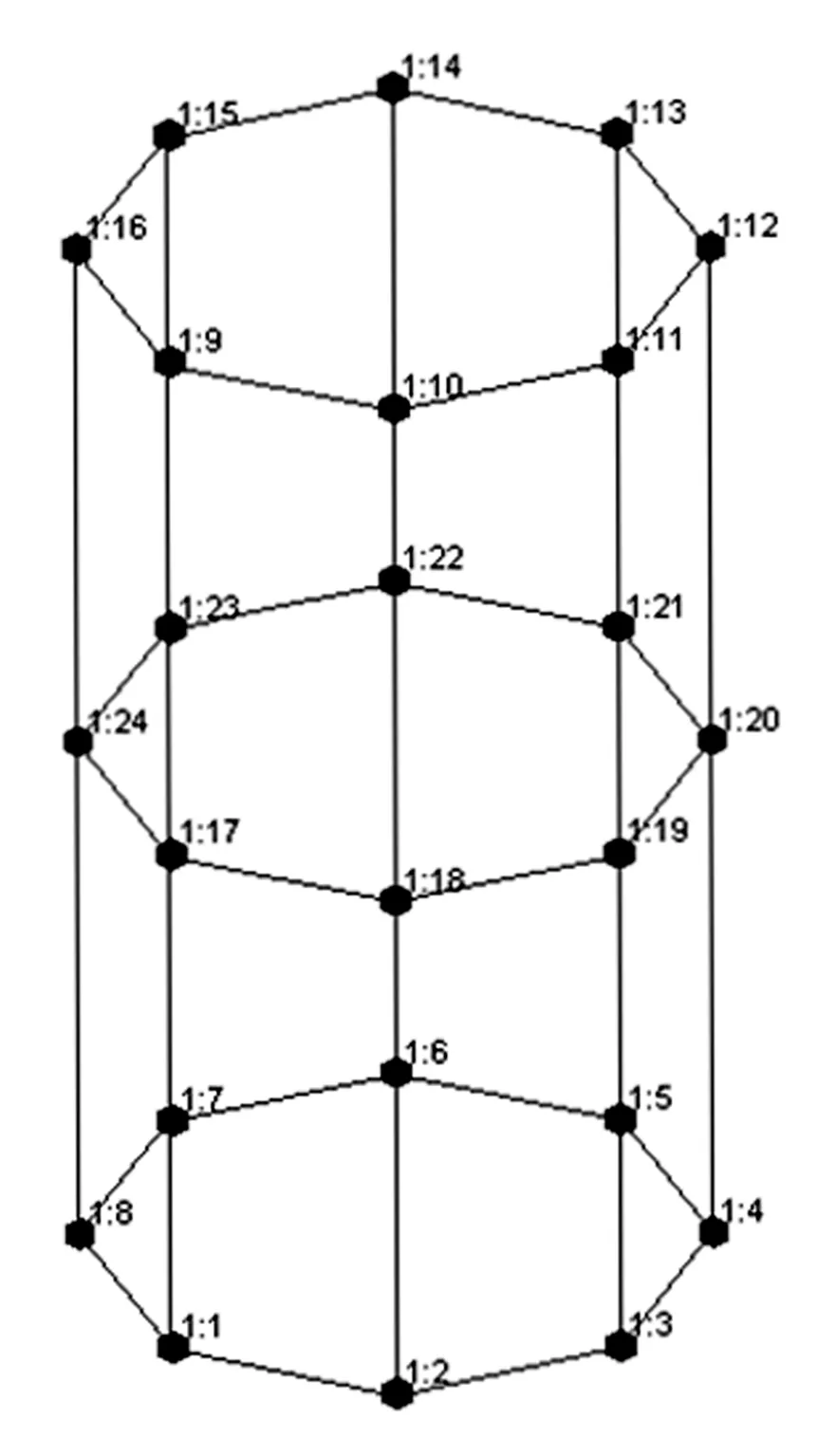
图4 试验件敲击点Fig.4 Knocking point of test piece

基于上文的建模方法和实验方案,得到螺栓连接的薄壁柱壳结构在自由边界条件下的前6阶固有频率和振型,并将有限元结果与实验结果进行对比.具体频率对比结果和振型对比结果分别如表1和图5所示,其中,第1阶、第2阶、第4阶和第6阶模态为结构向波数振型,第3阶模态为结构扭转振型,第5阶模态为结构剪切搓动振型.需要说明的是,本文采用fni代表第i阶固有频率.

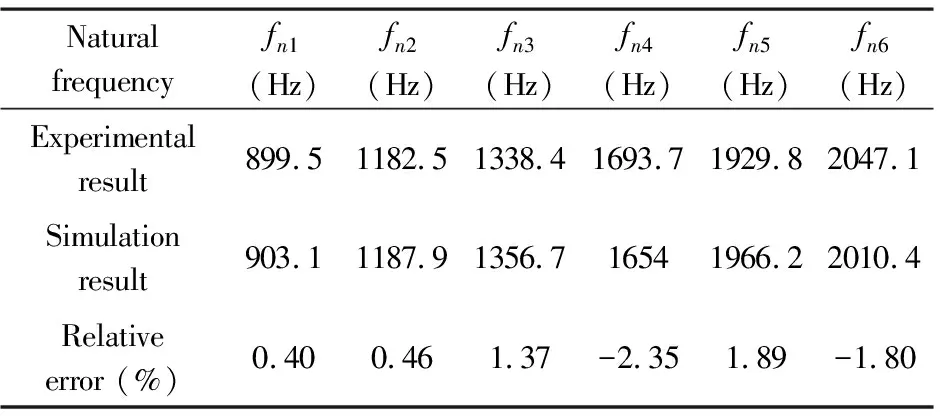
表1 前6阶仿真与实验结果固有频率对比Table 1 Comparison of the first 6 order natural frequencies between simulation and experimental results

Note: error=(simulation-experiment)/experiment

2 螺栓连接旋转薄壁筒固有特性分析

本小节考虑旋转软化、离心刚化和陀螺效应,对螺栓连接薄壁柱壳结构施加转速效应,分析螺栓预紧力和转速耦合作用下对系统固有特性的影响.仿真参数设置如下：预紧力的变化范围为800～3000 N,转速分别为0 r/min、3000 r/min、6000 r/min.通过ANSYS仿真软件,得到系统的前6阶固有频率随预紧力和转速的变化曲线如图6所示.

观察图6可知：

(1)随着螺栓预紧力的增加,系统的前6阶固有频率不断增加,预紧力越大,系统的前6阶固有频率增加程度越小,这是因为,螺栓预紧力越大,左右两筒结合的越牢固,结合面的连接刚度越大,从而导致系统的固有频率不断增大.

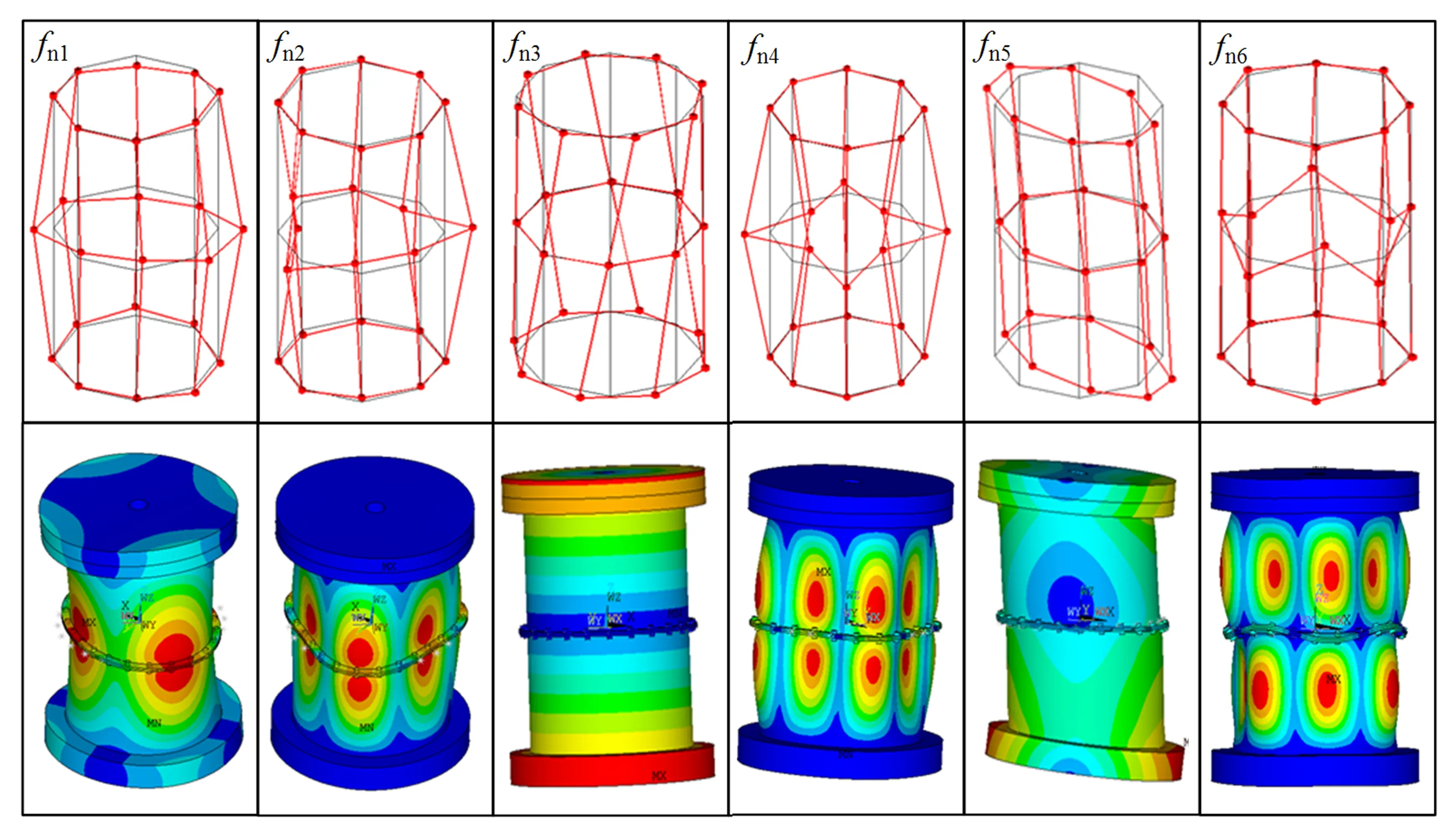
图5 仿真与实验振型图对比Fig.5 Comparison of simulation and experiment mode shapes

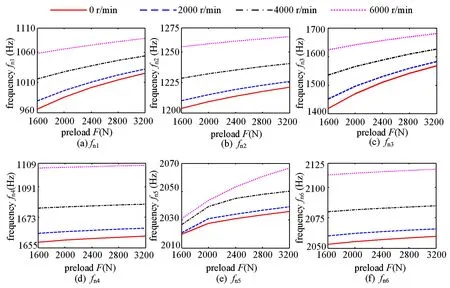
图6 不同预紧力和转速下系统前6阶固有频率Fig.6 The first 6 natural frequencies of the system under different preload and speed

(2)随着系统转速的增加,系统的前6阶固有频率不断增加,转速越高,结合面的接触面积增大,系统的刚化效应越明显,从而导致结合面的接触刚度和系统的整体结构刚度越大,系统的固有频率不断增大.

(3)预紧力足够大时,系统的固有频率的变化主要是由于转速引起的,也间接说明转速对其固有特性的影响程度要大于预紧力对其固有特性的影响.

3 结论

本文以螺栓连接薄壁柱壳结构为研究对象,首先基于ANSYS有限元分析软件,建立精细有限元模型,其次通过与自由边界条件下实验得到的振型和固有频率对比,验证仿真模型的准确性和有效性,最后,探究了螺栓预紧力和系统转速耦合作用下对结构固有特性的影响规律.结论如下：

(1)在对螺栓连接薄壁柱壳结构进行模态求解时,基于接触的预应力模态法计算精度较高,仿真与实验结果最大误差约为-2.35%,证明本文建立的螺栓连接薄壁筒结构精细有限元模型的准确性和合理性.

(2)随着转速和预紧力的增加,结合面的连接刚度和系统的结构刚度不断增加,系统的前6阶固有频率不断增加,转速较低时,预紧力对系统的固有特性的影响占主导；当预紧力足够大时,系统的固有频率的变化主要是由转速引起.