轴承预紧力对转子系统静动态特性的影响*
赵耿 刘保国 冯伟 王攀
(河南工业大学 机电工程学院, 郑州 450000)
引言
精密角接触球轴承因其旋转精度高、承载能力强等特点而广泛应用于各类机床主轴以及精密旋转机构中. 对于角接触球轴承,常采用轴向预紧的方式来提高其支撑刚度,合适的预紧力不仅能够提高轴承支撑刚度,对改善轴承-转子系统的性能也十分有利[1,2].
角接触球轴承的动力学特性分析一直都是众多研究人员的研究热点,Jones[3]、Harris[4]最早建立了角接触球轴承的五自由度分析模型,并考虑了轴承高速运转时滚珠离心力和陀螺力矩的影响.Houpertt[5]、Hernot[6]提出了角接触球轴承的五自由刚度矩阵形式,这使得借助有限元方法来解决轴承-转子系统的耦合问题成为可能. 曹宏瑞[7]、Cao[8]、王保民[9]、黄伟迪[10]等在拟静力学模型基础上建立了角接触球轴承的五自由度刚度计算模型,分析了预紧力对轴承刚度的影响.Jedrzejewski[11]通过建立轴承-转子模型研究了主轴转速以及轴承的预加载对轴承刚度所产生的影响. 饶成晨[12]、支汉立[13]等通过建立轴承-转子系统的有限元模型,针对影响电主轴工作性能的轴承-转子系统静动态特性进行了专门分析.
目前基于轴承理论模型先后开发了CYBEAN、ADORE等多款专门的分析软件,然而,采用计算程序分析角接触球轴承动力学特性,存在使用复杂、计算效率低等问题[14]. Romax软件不仅能够详尽分析角接触球轴承的刚度、寿命以及其内部载荷、接触应力等,也能够对轴承-转子系统进行动力学特性分析,包括振型分析、临界转速分析以及不平衡响应分析等. 本文基于Romax软件建立了5自由度轴承-转子系统动力学模型,研究了角接触球轴承刚度、工作接触角以及寿命等在轴承预紧力作用下的变化规律,并分析了预紧力对轴承-转子系统静变形以及振动响应的影响,可为轴承-转子系统的设计分析提供参考.
1 分析模型建立
对轴承进行动力学特性分析时将轴承-转子系统一起研究,能够更加真实可靠地反映轴承的工作性能[15]. 在Romax环境中对轴承-转子系统进行静动态特性分析不仅能够研究转子系统的动力学问题,也能够研究支撑轴承的动力学问题,分析更加符合工程实际. Romax中对轴承模型的建立需要输入轴承的结构参数对其进行实体建模,而后将轴承模型导入到转子系统建立完整的轴承-转子分析模型,系统模型结构如图1所示.

图1 Romax中轴承-转子系统二维模型Fig.1 2D model of bearing-rotor system in Romax
在Romax中可以考虑轴承5个方向的自由度,并能对轴承-转子系统在不同工况下的静动态特性进行分析. 图2给出了轴承在外载荷作用下五个方向的相对位移示意图. 本文以SKF公司角接触球轴承7004CD/P4DB为例进行研究,轴承主要结构参数如表1所示.

图2 轴承受力后内外圈五个方向相对位移示意图Fig.2 Diagram of relative displacement in five directions of inner and outer ringsunder loading force

表1 7004CD/P4DB轴承主要参数Table 1 Main parameters of SKF 7004CD/P4DB
2 预紧力对球轴承特性的影响
以SKF公司角接触球轴承7004CD/P4DB为例在Romax软件建立轴承-转子模型,研究主轴工作转速为12000r/min时,预紧力对角接触球轴承支撑刚度以及工作接触角的影响规律,并分析在动不平衡载荷作用下预紧力对轴承工作寿命的影响.
2.1 预紧力对角接触球轴承刚度的影响
图3给出了角接触球轴承径向刚度、轴向刚度以及角刚度随轴承预紧力的变化曲线. 随着轴承预紧力的增大,轴承径向、轴向以及角刚度均是增加的,表明增加预紧力对提升轴承支撑刚度是有利的.

图3 轴承刚度随轴承预紧力的变化曲线Fig.3 Variation curve of the bearing stiffness with bearing preload
2.2 预紧力对角接触球轴承工作接触角的影响
图4、图5给出了轴承内外圈的工作接触角随轴承预紧力的变化曲线. 随着轴承预紧力的增大,轴承内外圈的工作接触角均增大. 从图中可以看出,轴承内外圈的工作接触角在轴承滚道内随着滚珠位置角的变化呈现出正弦变化趋势,产生原因为在滚动轴承运转过程中因径向载荷作用引起滚珠产生周期性振动[16];在预紧力一定情况下,轴承内圈的工作接触角要大于其外圈的实际工作接触角.
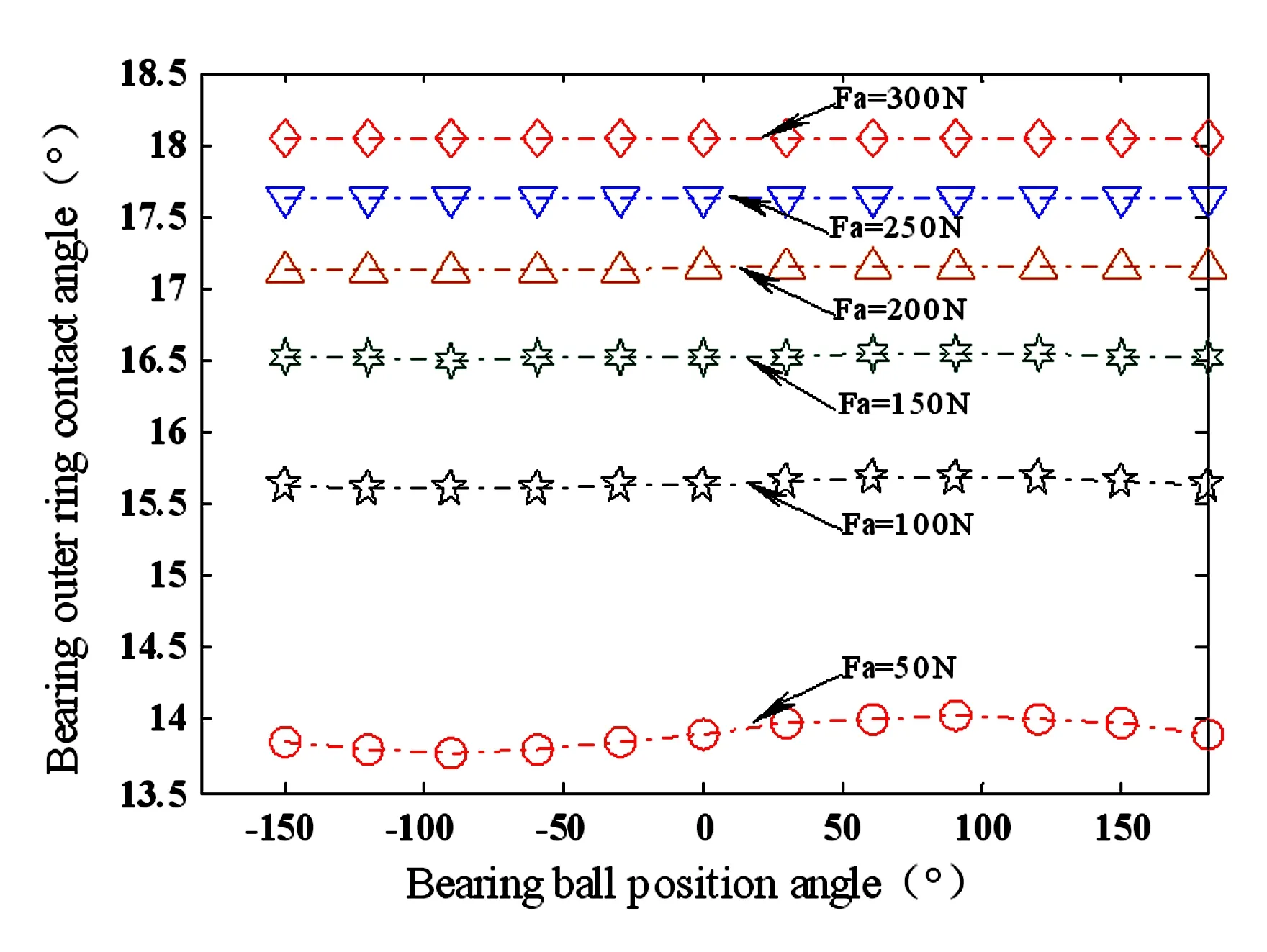
图4 轴承外圈接触角随轴承预紧力的变化曲线Fig.4 Variation curve of contact angle of the bearing outer ring with bearing preload
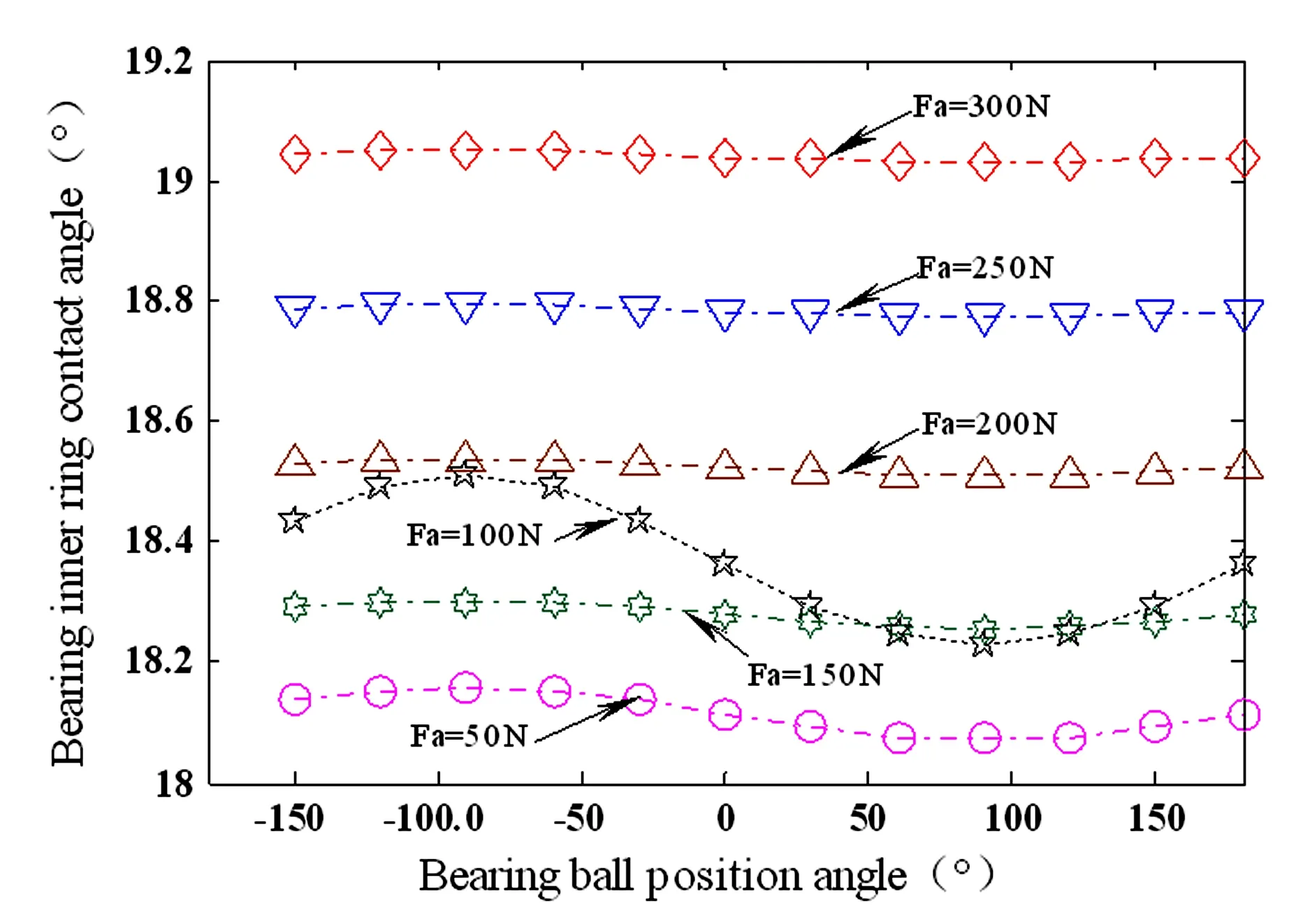
图5 轴承内圈接触角随轴承预紧力的变化曲线Fig.5 Variation curve of contact angle of the bearing inner ring with bearing preload
2.3 预紧力对角接触球轴承工作接寿命的影响
在 Romax中,轴承寿命包括模拟寿命和修正寿命,对应两种计算公式:一种是基于ISO的标准轴承寿命计算(模拟寿命),假设轴承中无内部间隙、轴承位置完全校准和一定比例的轴向和径向载荷等;另一种是基于真实工况的轴承寿命计算(修正寿命),考虑了轴承内部的间隙、轴承位置的错位误差和轴向及径向误差等.
图6给出了轴承工作寿命随轴承预紧力的变化曲线. 随着轴承预紧力的增大,轴承的工作寿命明显减小,且轴承的修正寿命要大于其模拟寿命,轴承的修正寿命更接近于其实际寿命[14].
从以上分析可以得出:增加预紧力虽然能够提升轴承支撑刚度,但会导致轴承寿命的减小. 故在实际工程中不能为提升轴承支撑刚度而一味增大其预紧力,应综合考虑选择合适的轴承预紧力.

图6 轴承寿命随轴承预紧力的变化曲线Fig.6 Variation curve of the bearing life with bearing preload
3 轴承-转子系统静动态特性分析
图7所示为搭建的轴承-转子测试试验台,信号采集装置为电涡流位移传感器系统. 结合本试验台研究了轴承预紧力对转子系统静刚度、固有频率的影响以及在动不平衡载荷作用下,转子系统在不用预紧力下的振动响应情况.

图7 轴承-转子测试试验台Fig.7 Test bench for bearing-rotor testing
该试验台通过螺栓紧固轴承端盖对轴承施加轴向预紧力,预紧装置如图8所示. 综合考虑预紧装置空间结构尺寸、装置的简易性以及操作的便捷性等,轴承预紧力通过标定好的压力传感器来确定,具体步骤为:当紧固螺钉时,用万用表测出安装在轴承端盖与隔套接触端面间的压力传感器的电阻值,然后对比其标定曲线确定对应的压力值.
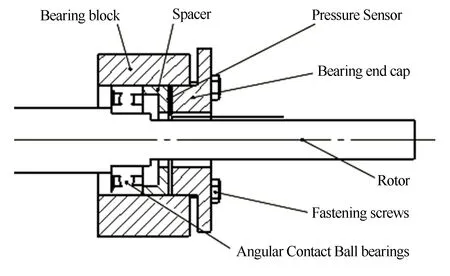
图8 轴承预紧结构示意图Fig.8 Bearing preload structure
3.1 预紧力对轴承-转子系统静刚度影响
在径向加载力为100N时,转子系统在不同预紧力作用下轴端静变形量的变化曲线如图9所示. 随着轴承预紧力的增大,轴端变形量减小,转子系统静刚度增大;轴端变形的仿真结果和试验结果存在一定误差,误差范围在13%以内(包含试验台零部件的加工误差和装配误差等),表明仿真结果是可靠的.

图9 转子系统轴端静变形量随轴承预紧力的变化曲线Fig.9 Variation curve of the static deformation of the shaft end of the rotor system with bearing preload
3.2 预紧力对轴承-转子系统振动响应影响
图10给出了转速为3000r/min时,不同预紧力作用下转子振动响应幅值随预紧力的变化曲线. 随着轴承预紧力的增大,转子的径向响应幅值呈减小趋势,表明增大轴承预紧力能够提高转子系统动刚度. 从图中看出,测试结果与仿真结果能够很好地匹配,误差范围在15%以内,表明所建模型的模拟仿真结果是可靠的.
3.3 预紧力对轴承-转子系统固有频率影响
图11给出了用Romax计算的轴承-转子系统固有频率随轴承预紧力的变化曲线. 如图所示,随着预紧力的增大,系统的1阶固有频率变化很小,2阶固有频率增幅较小,3阶固有频率有明显增大趋势. 结果表明,增加预紧力有利于提升转子系统的固有频率,这对于其动态性能的提升是有利的.

图10 转子系统径向响应幅值随轴承预紧力的变化曲线Fig.10 Variation curve of radial response amplitude of the rotor system with bearing preload

图11 轴承-转子系统固有频率随轴承预紧力的变化曲线Fig.11 Variation curve of natural frequency of the bearing-rotor system with bearing preload
4 结论
本文基于Romax建立了5自由度轴承-转子系统动力学模型,研究了轴承预紧力对角接触球轴承动力学特性的影响;结合所搭建的轴承-转子测试试验台,研究了轴承预紧力对轴承-转子系统静动态特性的影响,得到如下结论:
1)随着预紧力的增大,轴承的轴向刚度、径向刚度以及角刚度均显著增加,但其工作寿命急剧减少. 所以在对轴承预紧时,应在保证其工作寿命的情况下施加预紧力,以达到刚度和寿命的兼顾平衡;
2)预紧力对轴承的工作接触角影响十分明显,内外圈的工作接触角均随着预紧力的增加而增大;轴承内圈的实际工作接触角要大于外圈的实际工作接触角;
3)在径向静载荷作用下,随着轴承预紧力的增大,转子系统的轴端静变形量均呈减小趋势,且仿真结果和试验结果误差在13%以内;
4)在动不平衡载荷作用下,轴承-转子系统的振动响应幅值随着预紧力的增加而减小,且仿真结果和试验结果的误差在15%以内;增加轴承预紧力有利于提高系统的固有频率,且阶数越高其增幅越大;
通过本文研究,表明Romax能够很好地解决轴承-转子系统的耦合问题,为轴承-转子系统的耦合问题研究提供参考.

