低速轴向气流中曲壁板的稳定性及分岔分析*
李晋 李鹏 张德春 杨翊仁
(西南交通大学 力学与工程学院, 成都 610031)
引言
随着高速列车设计及运行速度的增加,之前在列车设计中被合理忽略的气动力问题已经逐渐凸显出来[1-3].为满足流线型设计要求,在高速列车设计及制造中会大量采用具有一定初始曲率的壁板结构,如列车蒙皮和车窗等.依照目前高速列车的设计速度推算,气流马赫数大约在0.3左右,基本上处于低亚音速范围.壁板受气流激扰而产生振动并会影响结构的安全服役[3,4],因此有必要对这类结构在低亚音速轴向流中的气动弹性问题进行一些基础性的研究.
针对曲壁板气动弹性问题的研究,已有的工作主要集中在航空航天领域,并且是以超音速气流中的壁板为主[5-8].文献[7-8]采用了活塞气动力理论,应用Von Karman非线性应变位移关系,研究了超音速曲壁板颤振的临界动压、极限环响应及混沌运动.而针对低亚音速气流中的壁板,相关研究还多局限于平板结构,对曲壁板的研究还相对不够完善[9-11].文献[9]基于势流理论及线化边界条件推导了平壁板上的气动力分析了壁板的失稳特性.文献[10]基于势流点源基本解并利用微分求积法研究了平壁板在不同边界条件下的失稳问题.文献[11]基于壁板模态采用级数方法获取了曲壁板上的气动力,研究了曲壁板的分岔特性及多平衡点的吸引域问题,但文中的气动力计算方法缺乏风洞实验验证.
本文考虑结构的几何大变形,利用能量方法建立了曲壁板的非线性振动方程.基于薄翼理论推导了曲壁板表面气动力的近似表达式,并设计风洞实验验证了该气动力公式的准确性.随后应用该气动力着重研究了曲壁板系统在气流作用下的稳定性及分岔特性.
1 力学模型及控制方程
考虑如图1所示的两端简支二维曲壁板,其密度、长度、厚度分别为ρ、l、h,壁板中点的初始拱高为He,且h≪l,He≪l.定义x方向为系统的轴向方向,沿着该方向在壁板上作用有面内力Fx;壁板上表面有均匀的低速轴向气流流过,气流的密度和速度分别为ρ∞和U∞;壁板材料为Kelvin型粘弹性材料,其弹性模量为E,粘性阻尼系数为gs.
考虑板的梁式变形并基于能量法可建立如下的曲壁板运动微分方程[7,8,11,12]:
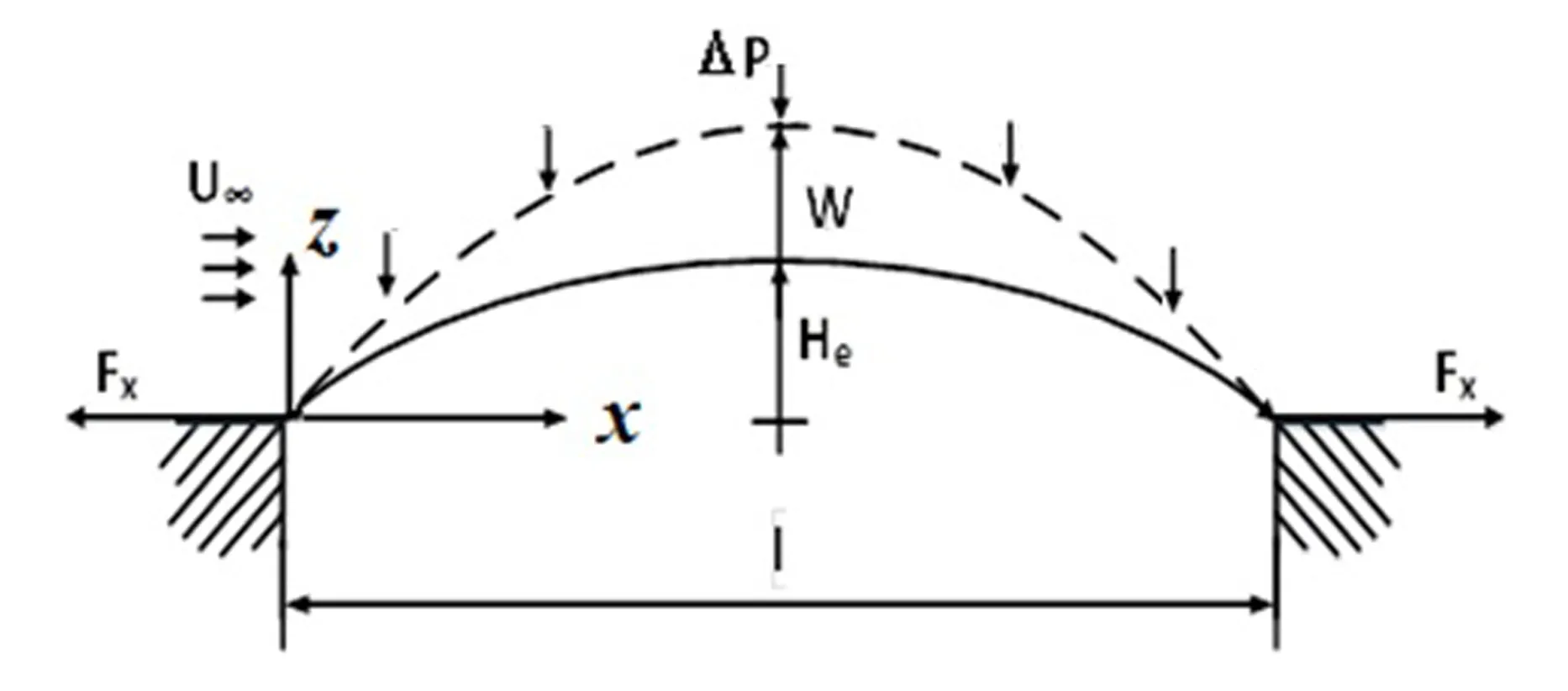
图1 轴向流中的二维曲壁板Fig.1 A two-dimensional curved plate in an axial flow
(1)
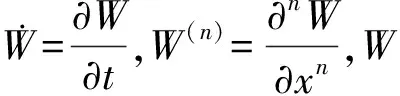
(2)
而ΔP=ΔPd+ΔPs为作用在壁板表面的气动压力,包括分别与曲壁板动扰度及初始变形相关的动态压力ΔPd及静态压力ΔPs两部分.
考虑无粘无旋不可压缩气流,基于薄翼理论,气流的扰度速度势函数[9,10]可写作:
(3)
由伯努利方程可得壁板表面的动态压力:
(4)
将(3)带入(4)可得:
(5)
对式(5)的第二项进行分部积分后可得:
(6)
将式(6)的前半部分在x0=x处进行泰勒展开并取第一项可得压力ΔPd:
(7)
其中,
(8)
式(7)最后一项表征了壁板边界条件对气动力的影响.考虑壁板的初始变形W0,忽略(7)中的时变项可得相应的静态气动力ΔPs:
(9)
从上式可知,壁板上的静态压力主要与壁板初始变形的曲率相关.
2 气动力的实验验证
为了验证式(7)给出的气动力计算公式的准确性,本节设计并完成了相关的风洞实验.为保证验实验的一般性,实验中并未采用图1所示的简支壁板及其初始构型,而是采用具有变曲率初始构型的铝合金板进行吹风实验并测试壁板表面的静态压力.沿着壁板中轴线(来流方向)开有5个直径为2mm的小孔用于安装压力传感器(型号:XCQ-093),开孔位置如图2所示.为保证单侧受流,壁板安装在导流装置上,该导流装置安装在刚性支架上,由一个近似封闭的空腔构成(空腔内填充有海绵,内部流体可视为静止).导流装置的前导流面与前缓冲区域可保证流场在受扰动后流经壁板模型处的气流仍是均匀的.壁板两端固支并采用胶布封闭其上下两侧,其安装方式如图3所示.
吹风实验在直径1.2m的开口环流式风洞中完成,该风洞优质稳定的风速范围为15~30m/s.对实验模型在此风速范围内进行三组吹风实验,测试各点的压力值并计算平均值.测试得到的壁板表面各点的压力系数如图4所示.
从图4可知,曲壁板表面主要为负压区,压力值随风速的增加而增加;靠近曲壁板的前后缘处存在较小的正压区;各测试点的压力系数Cp随风速变化基本保持平稳.由于测点1与5,2与4呈近似对称分布,因此这些点的压力系数也近似相等.图5展示了实验用曲壁板的初始构型及其对应的拟合函数曲线,从图可知该实验曲壁板模型具有变曲率的初始构型.将构型拟合函数W1带入式(9)计算得到气动力ΔPs1.文献[11]考虑无限长波形壁板,利用模态展开法得到了近似气动力(本文记为ΔPs2).由图6可知,与文献[11]相比,本文的计算结果与实验吻合地更好,能够准确反映壁板上的压力分布(每个风速下的压力值均已除以其最大值).
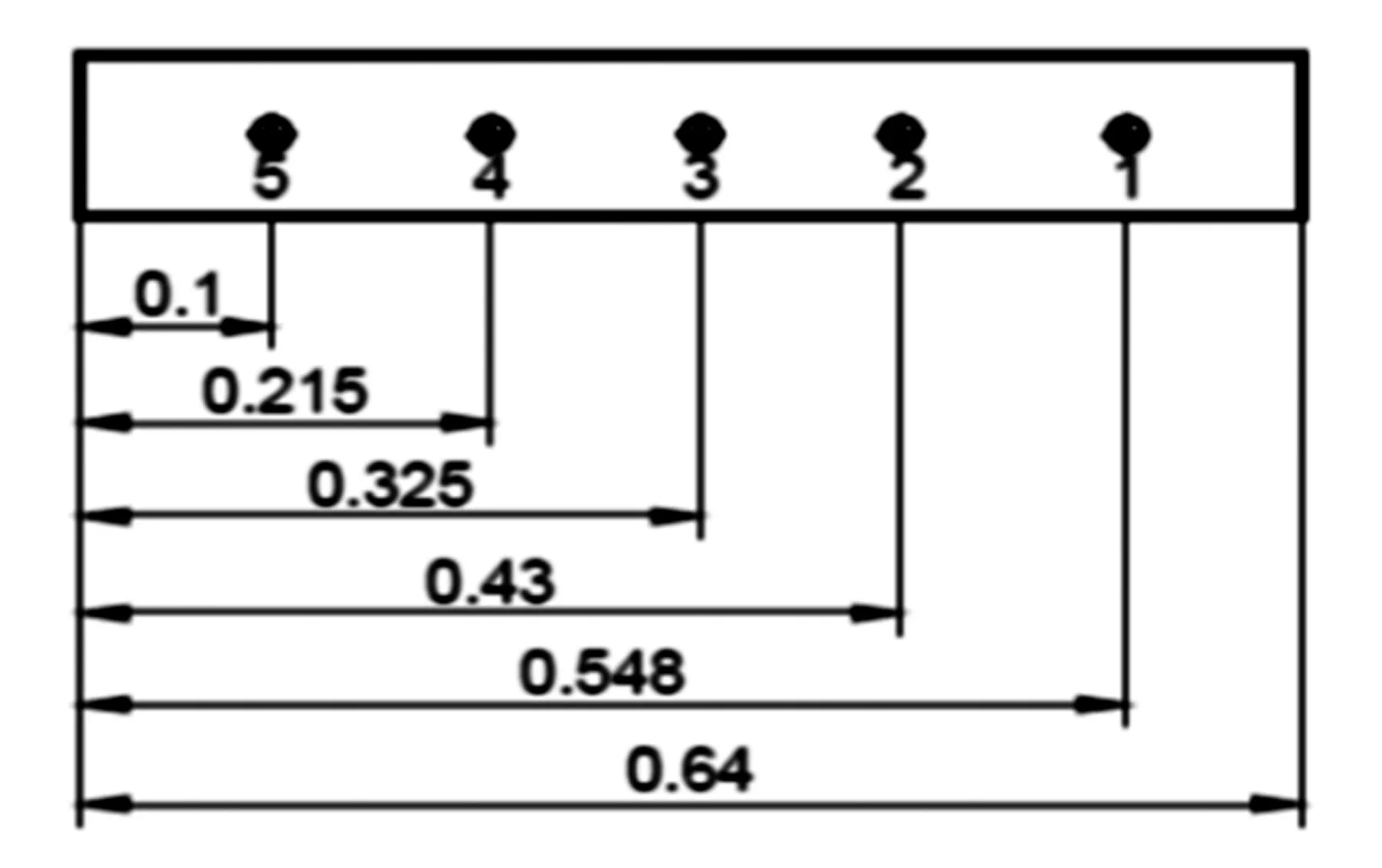
图2 压力传感器安装位置示意图(单位:m)Fig.2 Installation sketch of the location of pressure sensors

图3 曲壁板试验安装图Fig.3 Installation sketch of a curved plate in wind tunnel
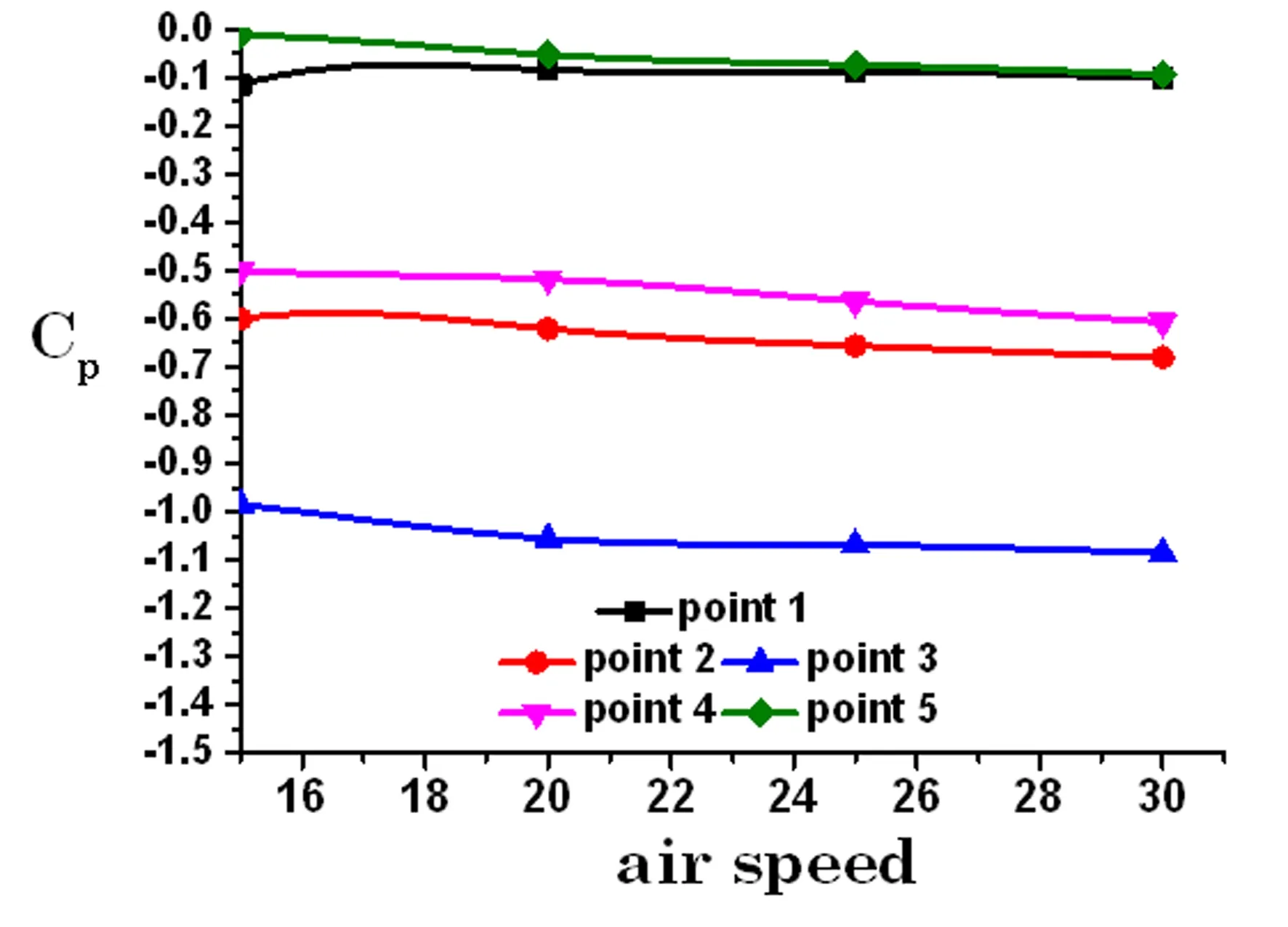
图4 实验曲壁板各测点压力系数随风速变化图Fig.4 The pressure coefficients of the curved plate
需要指出的是:1)由于实验壁板的宽度不足而未完全满足二维流场假设,会导致壁板背风面气动力理论计算与实验结果存在一些误差,但已有结果表明沿实验(三维)壁板中轴线布置的测点可以相对准确地描述二维流场的特性. 2)由于理论计算中并未计及壁板前后刚性导流段的影响,因此会导致在壁板前后缘处气动力的理论计算与实验结果存在一些偏差. 但在本文以下的计算中,由于曲壁板前后缘均有固定的位移约束,其对系统稳定性并不会产生明显影响[11].上述这两点正是作者们拟开展的工作内容.
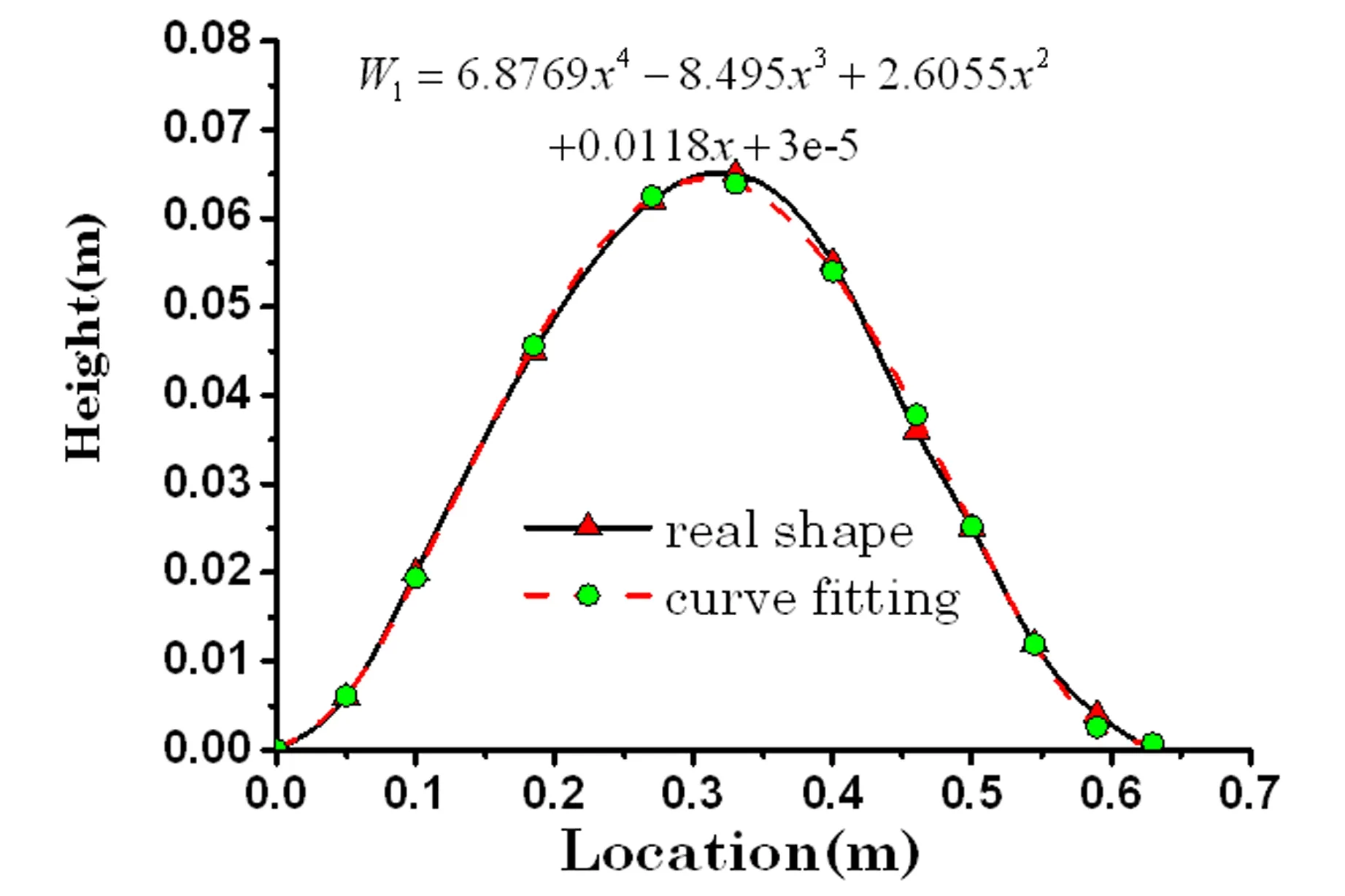
图5 实验曲壁板初始构型及拟合曲线图Fig.5 The initial configuration of the curved plate and its fitting curve
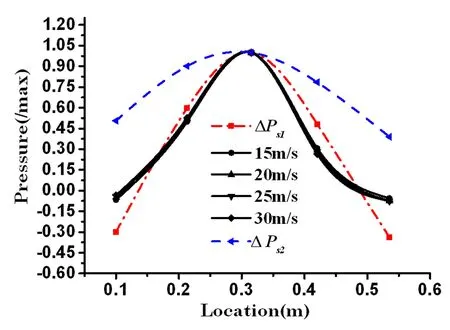
图6 气动压力理论计算及实验结果对比图Fig.6 Comparison of the theoretical and experimental pressure
3 静变形及静态分岔
在上节中已采用具有变曲率初始构型的实验曲板验证了本文气动力的准确性.下面采用式(7)、(9)计算式(1)中的气动力并分析曲壁板的稳定性问题.为方便理论计算并与已有文献[7,8]进行对照,下面的理论分析中将选择具有常曲率的圆柱面作为曲壁板的初始变形,该初始构型构型可描述为:
(10)
进一步考虑该曲壁板的两端简支条件,选用N个正弦模态,利用Galerkin方法离散式(1)后可得如下的常微分方程组:
(i=1,2,…,N;j=1,2,…,N;k=1,2,…,N)
(11)
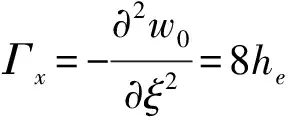
(12)
Mf,Kf,Cf分别为流体产生的附加质量矩阵、刚度及阻尼矩阵,Kt为由壁板边界条件引起的流体附加刚度矩阵.
选取高速列车常用的铝合金板为算例[2,3]:
E=69Gpa,υ=0.3,h=2.5mm,
ρ=2705kg/m3,l=0.8m,ρ∞=1.29kg/m3
在式(11)中取n=2进行计算可获得系统的动力特性.
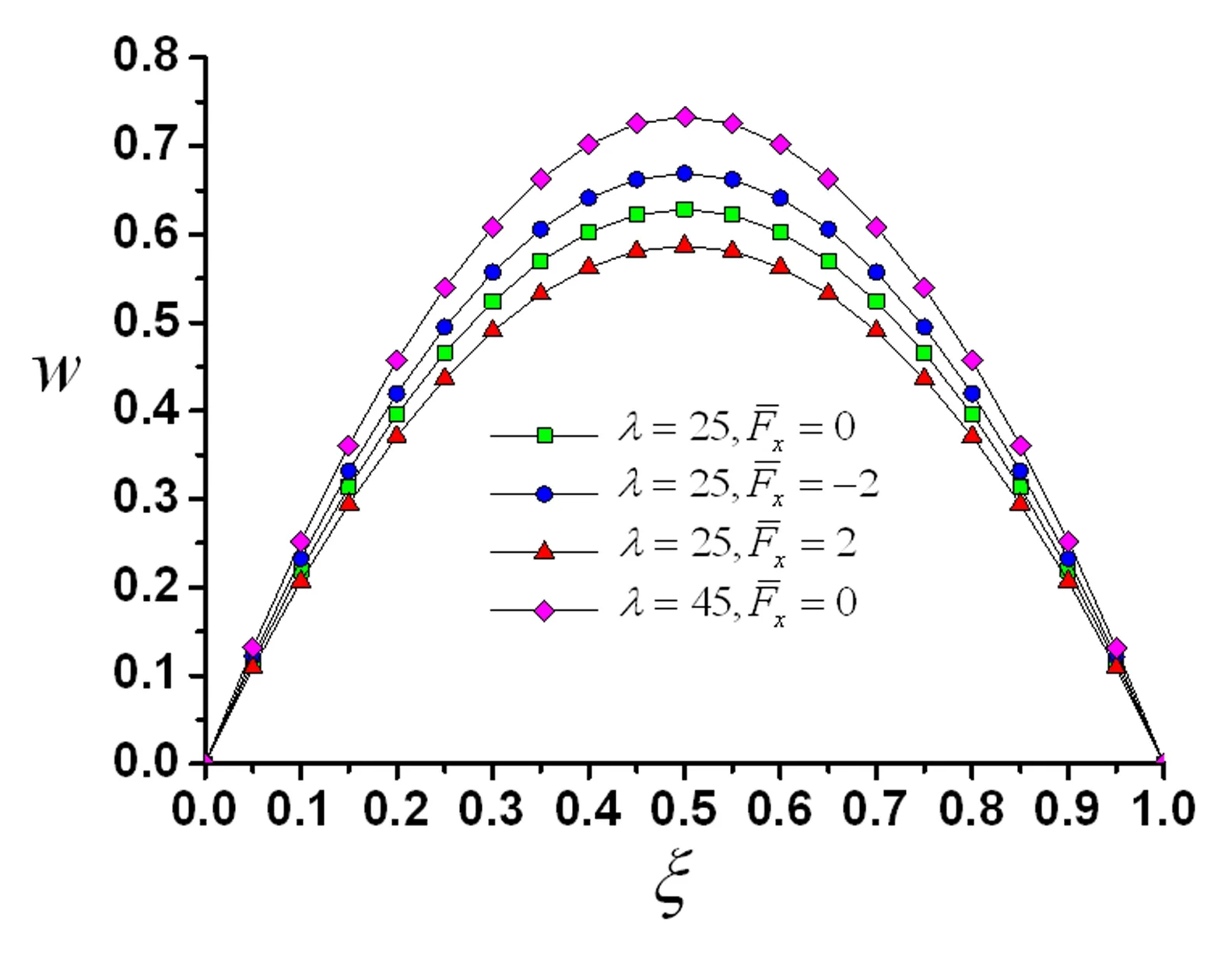
图7 曲壁板静变形图Fig.7 The static deformation of the curved plate
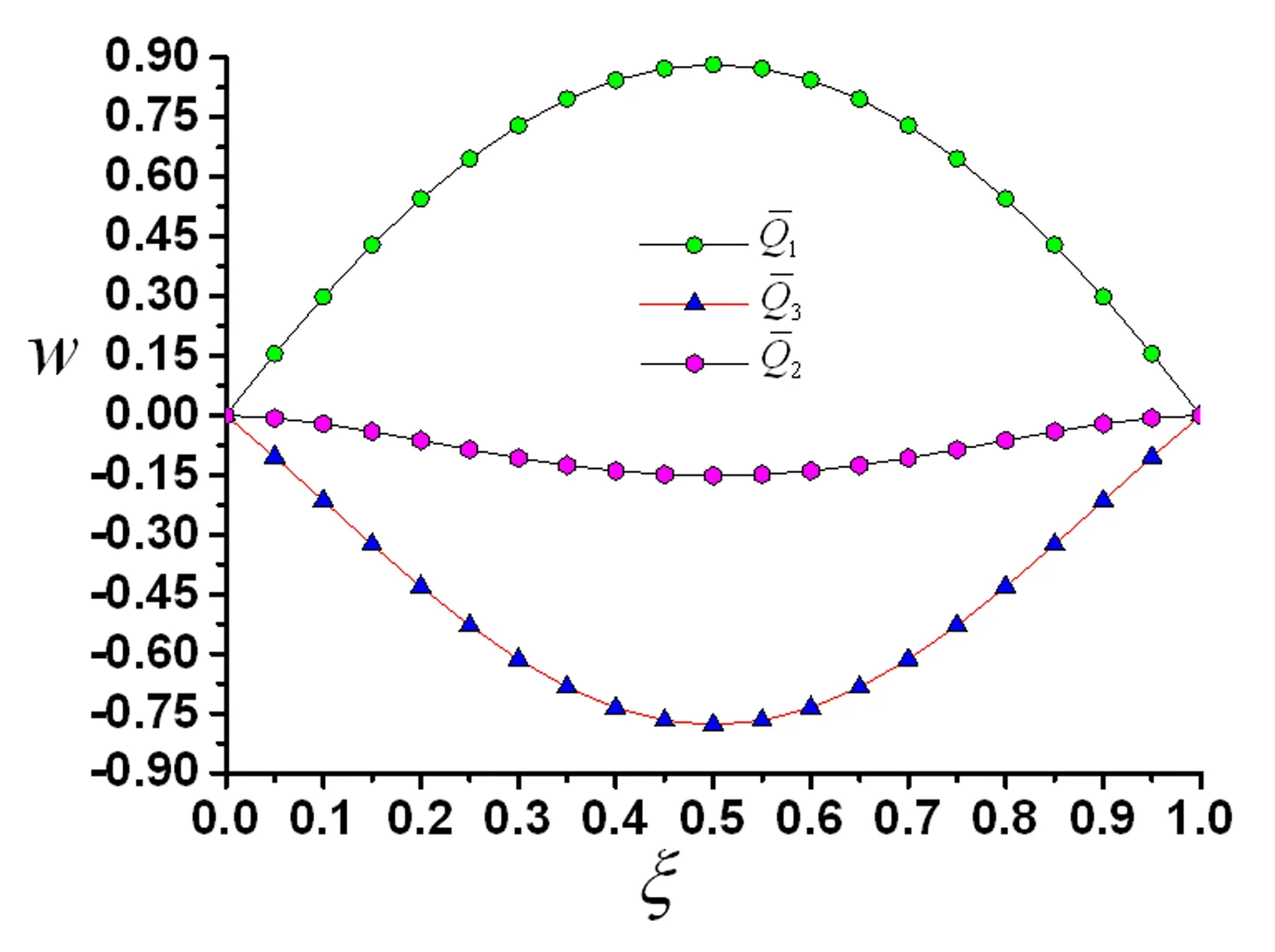
图8 当时曲壁板静变形图Fig.8 The static deformation of the curved plate for λ=75,
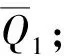
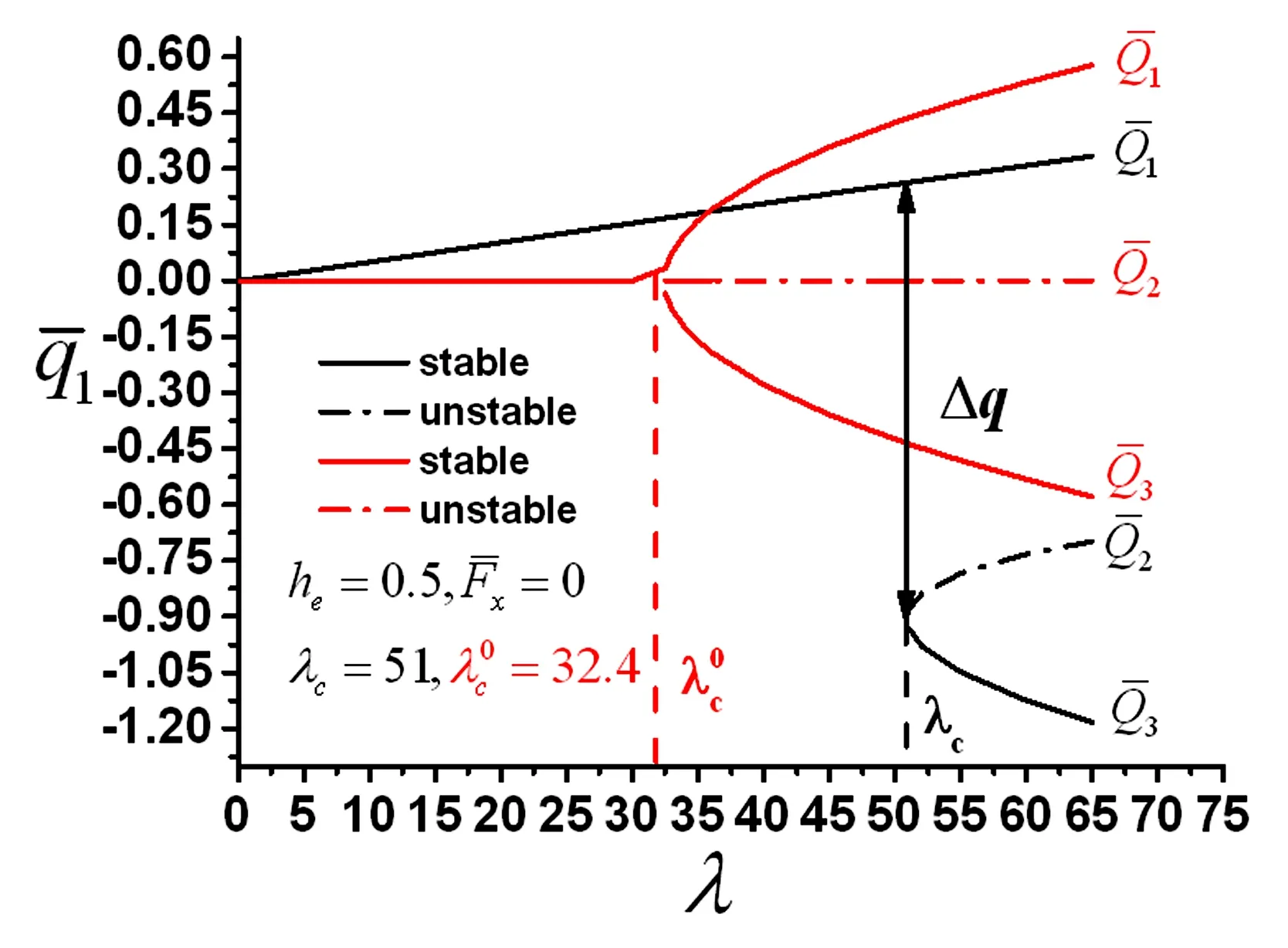
图9 平衡点随动压的变化Fig.9 The varying of equilibrium points as λ increasing
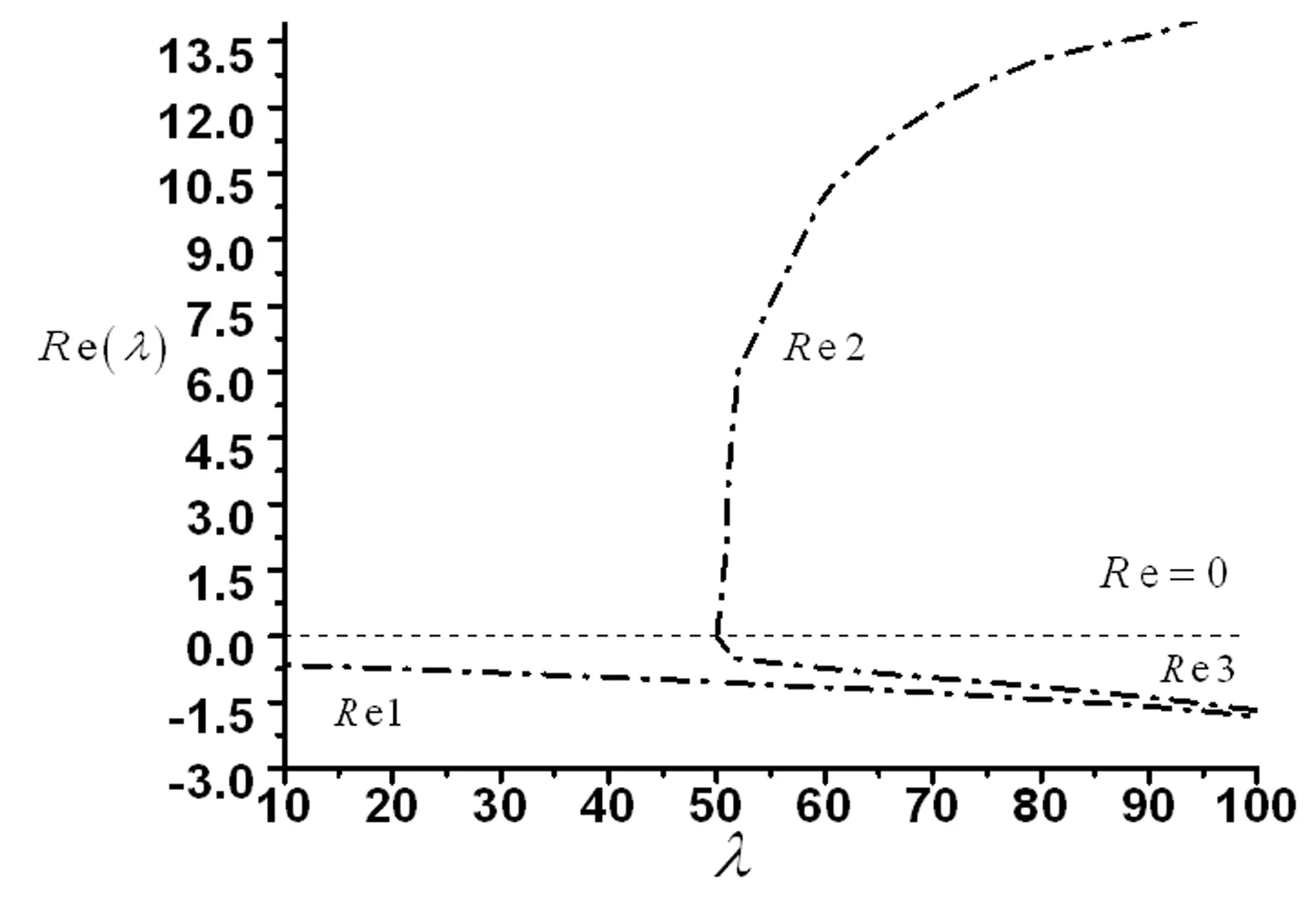
图10 特征值实部随动压变化Fig.10 The varying of eigenvalues as λ increasing
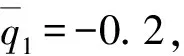
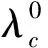
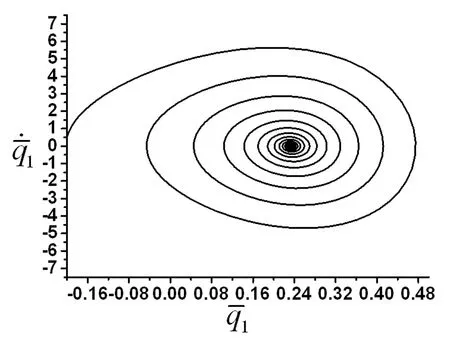
图11 λ=45时系统的响应相图Fig.11 Phase-plots of the system for λ=45
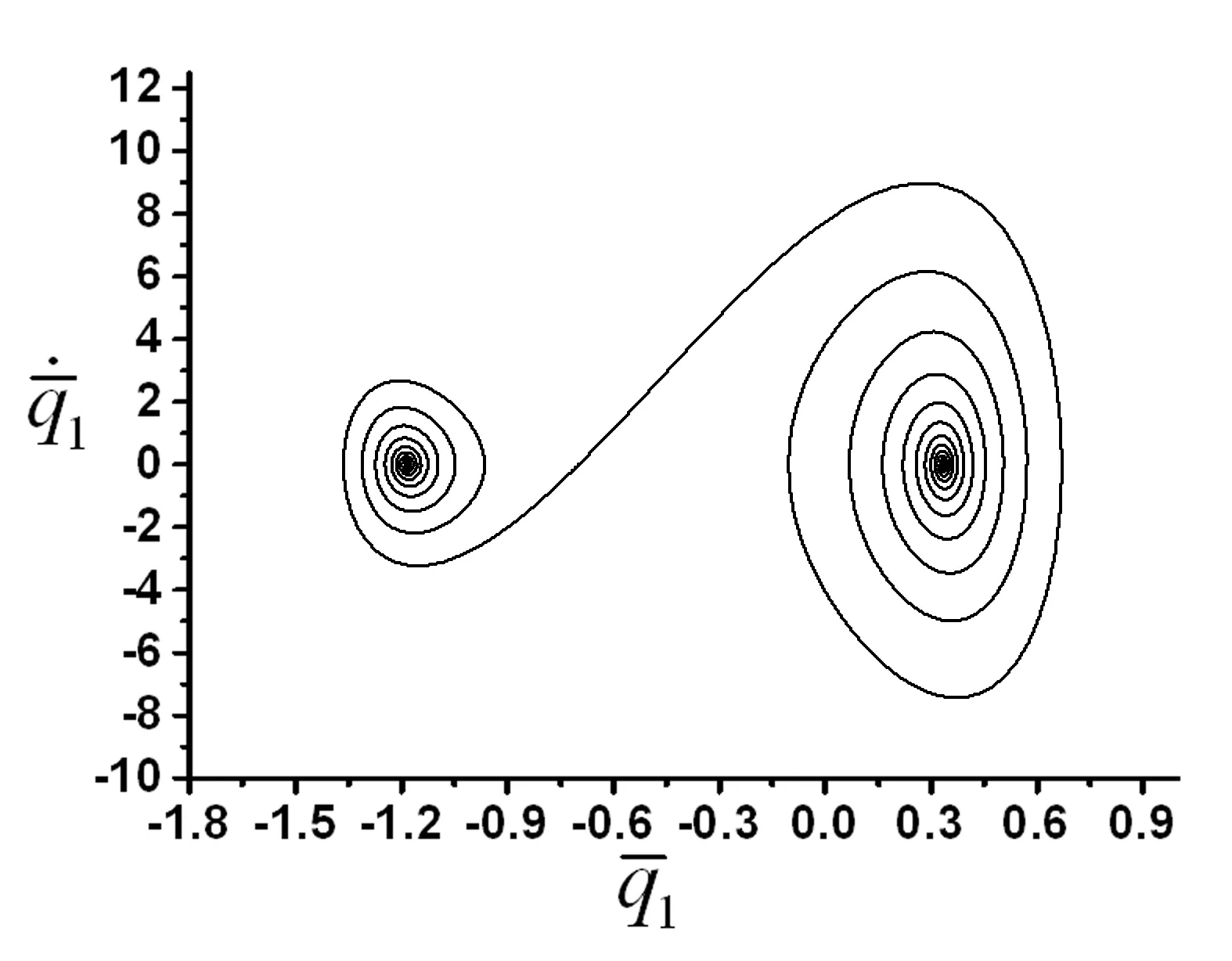
图12 λ=65时系统的响应相图Fig.12 Phase-plots of the system for λ=65
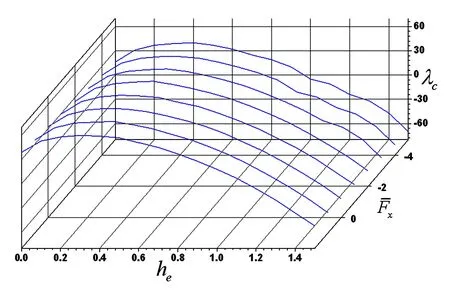
图13 λc随he及变化图Fig.13 The dependence of λcon heand
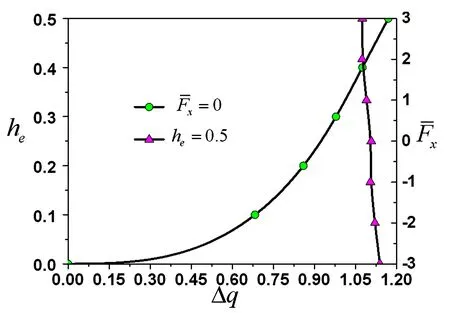
图14 跳跃值随参数的变化图Fig.14 The evaluation of Δ q as a function of heand
4 分岔结构分析
下面在参数空间内对系统的分岔结构进行分析.记曲壁板系统达到临界失稳状态时各参数满足方程:
(11)
而平板系统对应的临界动压则可表示为:
(12)
(13)
这三条曲线将该参数平面分成了如下的4个区域:
(14)
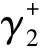
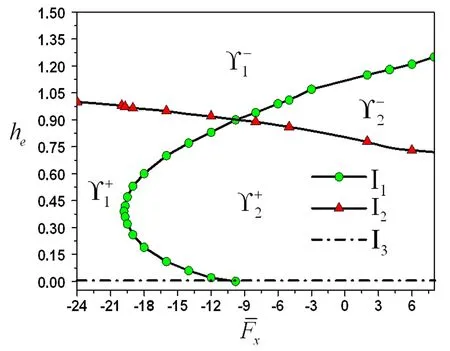
图参数平面图
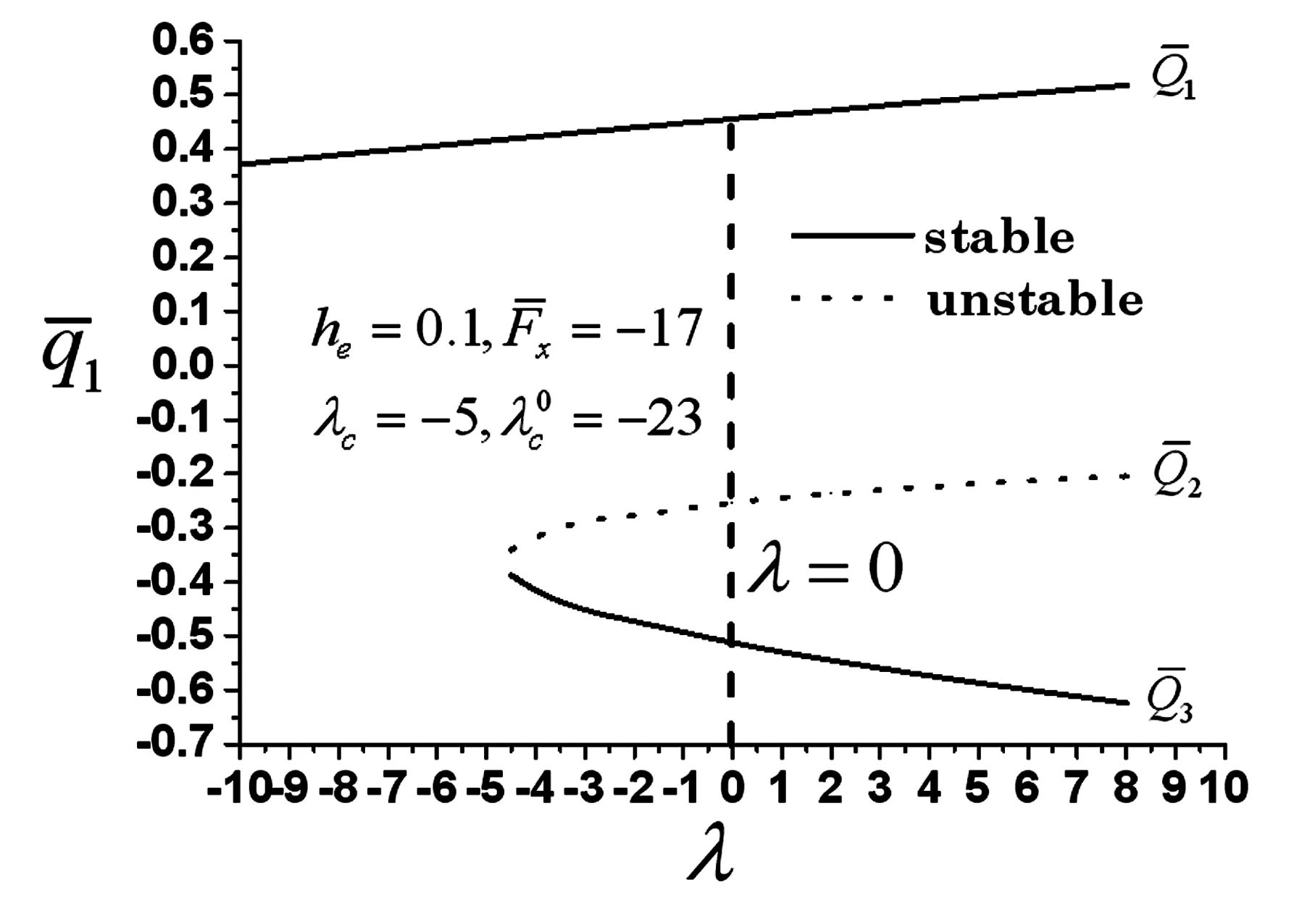
图区域中的分岔图Fig.16 Bifurcation diagram in region
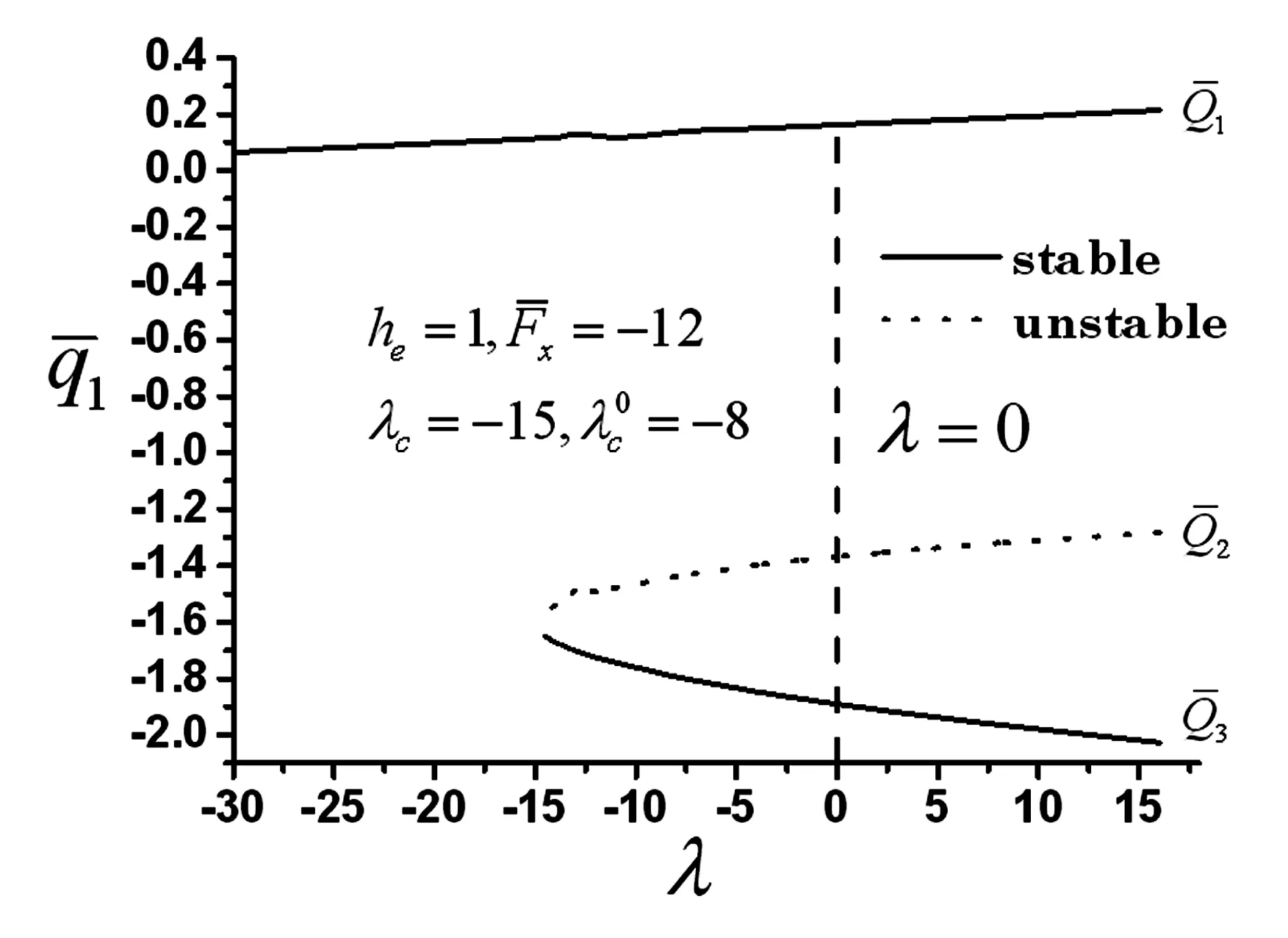
图区域中的分岔图Fig.17 Bifurcation diagram in region
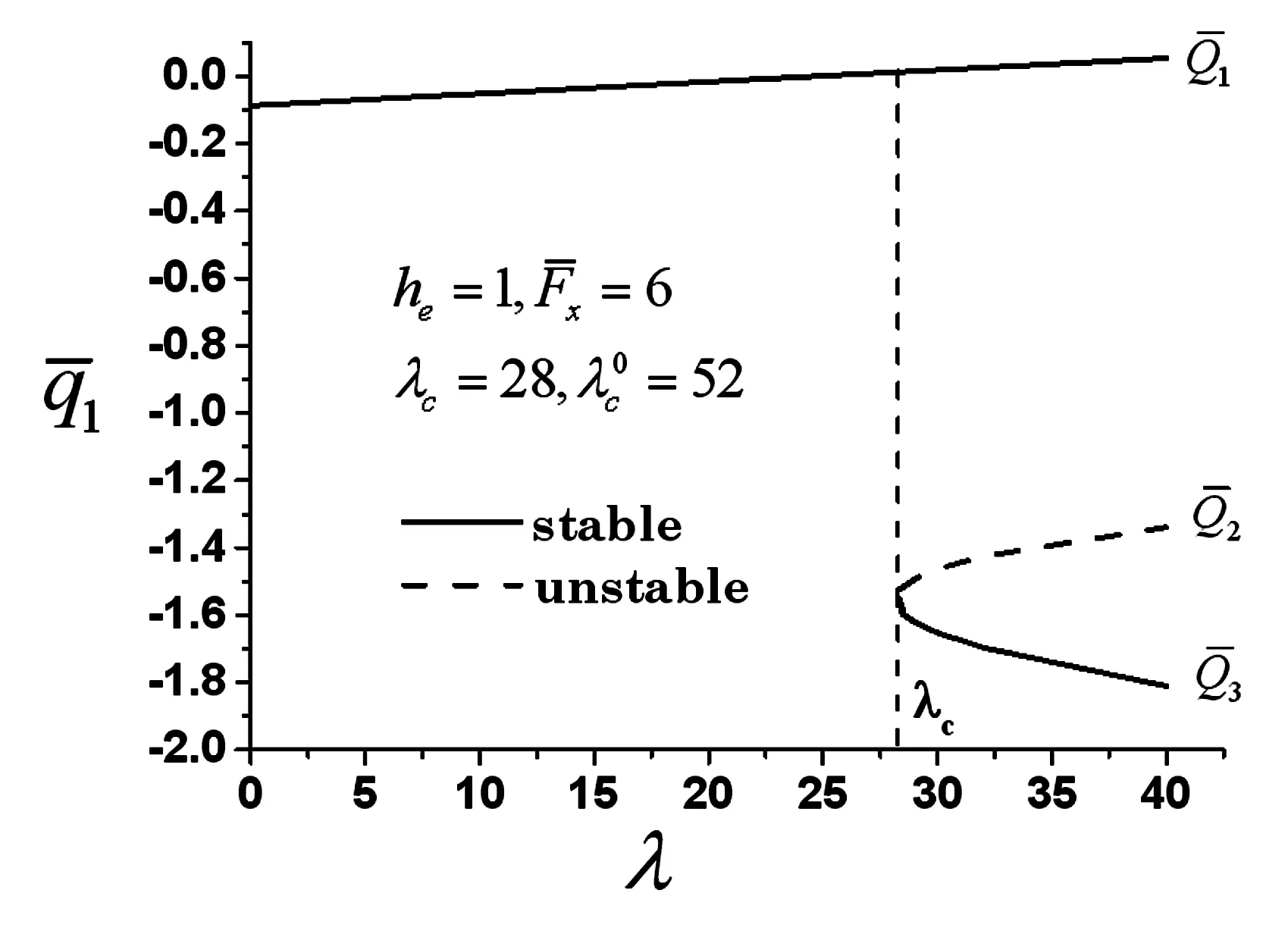
图区域中的分岔图Fig.18 Bifurcation diagram in region
5 结 论
(1)本文提出的气动压力计算方法与风洞实验吻合良好,表明了本文方法的准确性.曲壁板的变形量随来流速度的增加而增大,而随面内拉力(压力)的增加而减少(增大).
(2)由于静态气动力对系统对称性的破坏,曲壁板系统会发生非对称的静态分岔.该分岔同时伴随着平衡态的跳跃,跳跃值随初始几何曲率的增大而增大,而对面内力的变化并不敏感.系统的临界来流速度随面内拉力(压力)的升高而增大(减小),而随着初始拱高的增加呈现先增加后减小的规律.
(3)相对于平板而言,初始几何曲率及面内力的联合作用使得曲壁板系统的分岔行为更为丰富,会在不同参数区域出现四种分岔;增加面内拉力及适当增加曲壁板的初始拱高会提高系统稳定的参数区域,而面内压力及过大的拱高却不利于系统的稳定.

