不平行接触下的螺栓连接刚度及其转子动态特性*

闫平 邹存健 张伟 韩清凯 孙伟

(大连理工大学 机械工程学院, 大连 116024)

引言

航空发动机结构复杂,发动机转子的各阶固有频率和振型是结构承受动态载荷的重要参数,模态分析可以有效地预估这些参数并作为其他动力学分析的研究基础.螺栓连接结构是航空发动机转子中的常用结构,其广泛应用于低压涡轮轴、高压压气机等关键部件的连接,而其连接刚度对转子静动态力学性能有着至关重要的影响.要研究转子系统动力特性尤其是临界转速、振型、不平衡响应以及传递特性等都需要知道准确的刚度值[1].一个完整的螺栓连接结构是由螺栓、螺母以及被连接件组成的,由于制造和装配过程中产生的几何偏差会使得连接结构中的各结合面并不是理想的平面,往往会形成倾斜的平面,尤其是被连接件与螺母下部的结合面,其不平行接触对连接刚度和应力分布产生非常显著的影响[2-5].

在航空发动机转子模态分析方面,弓可[6]等提取了某型号航空发动机转子前六阶固有频率和振型,分析计算并判断出转子在工作转速内具有足够的振动安全裕度,不会产生共振.申苗[7]等对发动机双转子系统进行了固有频率及振型计算,通过改变轴承刚度来影响系统固有频率,使得临界转速避开工作区域,定性地研究了轴承刚度的改变对于双转子系统振动特性的影响.各国学者们对于螺栓连接刚度的理论计算及有限元分析也进行了大量的研究工作,Motosh[8]将螺栓假设为一个简化、等价的弹性体形状,以使常规的刚度和变形计算变得简单,并对一个无垫圈刚性节点的8种刚度估计方法进行了讨论,提出了刚度计算的理论模型；德国工程师协会[9]对被连接件的刚度计算做了反复修订并已经出版了用于估算偏心节点刚度的计算公式；Bickford[10]将被连接件的压应力分布区域等效为空心圆柱体、圆锥体与球体等形状,为刚度计算提供新的方法；杨国庆[11]等构建了半解析模型,分析了不同弹性模量、泊松比、装配间隙和厚度等因素对被连接件刚度的影响规律,提出了一种新的刚度计算半解析方法；王海涛[12]利用有限元方法得到了机匣弯曲刚度与螺栓预紧力的关系曲线,分析了机匣刚度的影响因素；Sethuraman[13]等把螺栓头和螺母支撑面简化为两种不同的结合面,施加均匀轴向位移及压力,预估被连接件的刚度范围.

在上述研究中,计算连接刚度以及变形时,各部分串联弹簧被假设为线性及完全弹性,但是实际工况下连接刚度并非如此,尤其在结构偏差存在的情况下,支撑面不平行接触下螺栓张紧的过程中,螺母会逐渐贴合被连接件端面,螺杆发生弯曲,节点中的各接触面将传递弯矩,使得原有刚度的计算方法误差增大,并使得螺栓连接结构的实际模态与理论计算结果误差较大.本文通过建立螺栓支撑面不平行接触下的拧紧过程有限元模型和模拟转子模态有限元模型,揭示了其对连接结构应力分布的影响机理,建立了结合面几何偏差与连接刚度以及结构模态的映射关系.

1 螺栓连接刚度有限元仿真

1.1 有限元模型

螺栓连接是通过螺栓-螺母夹紧被连接件,几何模型如图1所示(图中,d为螺栓公称直径；dh为螺栓孔直径；dw为支承面直径；θ为不平行角度；dm为被连接件外部直径；L为被连接件总厚度),这个部件组合的刚度按下式计算：

式中,KT为螺栓连接刚度,KL为被连接件刚度,KB为螺杆的刚度,KN为螺母的刚度.

在计算螺栓连接刚度和变形时,施加预紧力F,计算被连接件压缩量Δl,得到被连接件刚度.被连接件刚度表达式：KL=F/Δl.

在上、下被连接件接触面部分施加外加载荷T,接触反力为FN,如图1所示圆柱体单元所构成的体系中接触面分离距离为σ.螺栓连接刚度表达式：

KT=ΔFN/σ

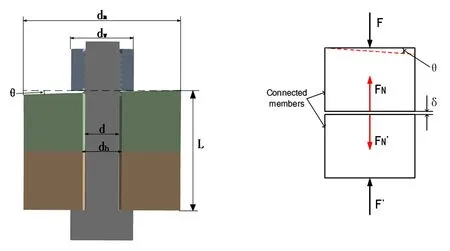
图1 螺栓连接结构几何模型Fig.1 Geometric model of bolted joint

为了分析不同平行度对螺栓连接刚度大小的影响,计算了7 种不同角度下的螺栓连接刚度,螺栓预紧力选取为30000N,接触面分离距离为0.01mm,被连接件外径为40mm,被连接件厚度为30mm.

为了分析不平行度偏差对于螺栓连接刚度大小的影响,建立了螺栓连接参数化有限元模型,如图2所示.模型由螺栓及上、下两被连接件组成,采用真实螺纹连接,设定被连接件厚度、内外螺纹中径、牙厚、螺距、牙型角、螺栓孔孔径,螺母外径、螺杆大径、不平行角度等.

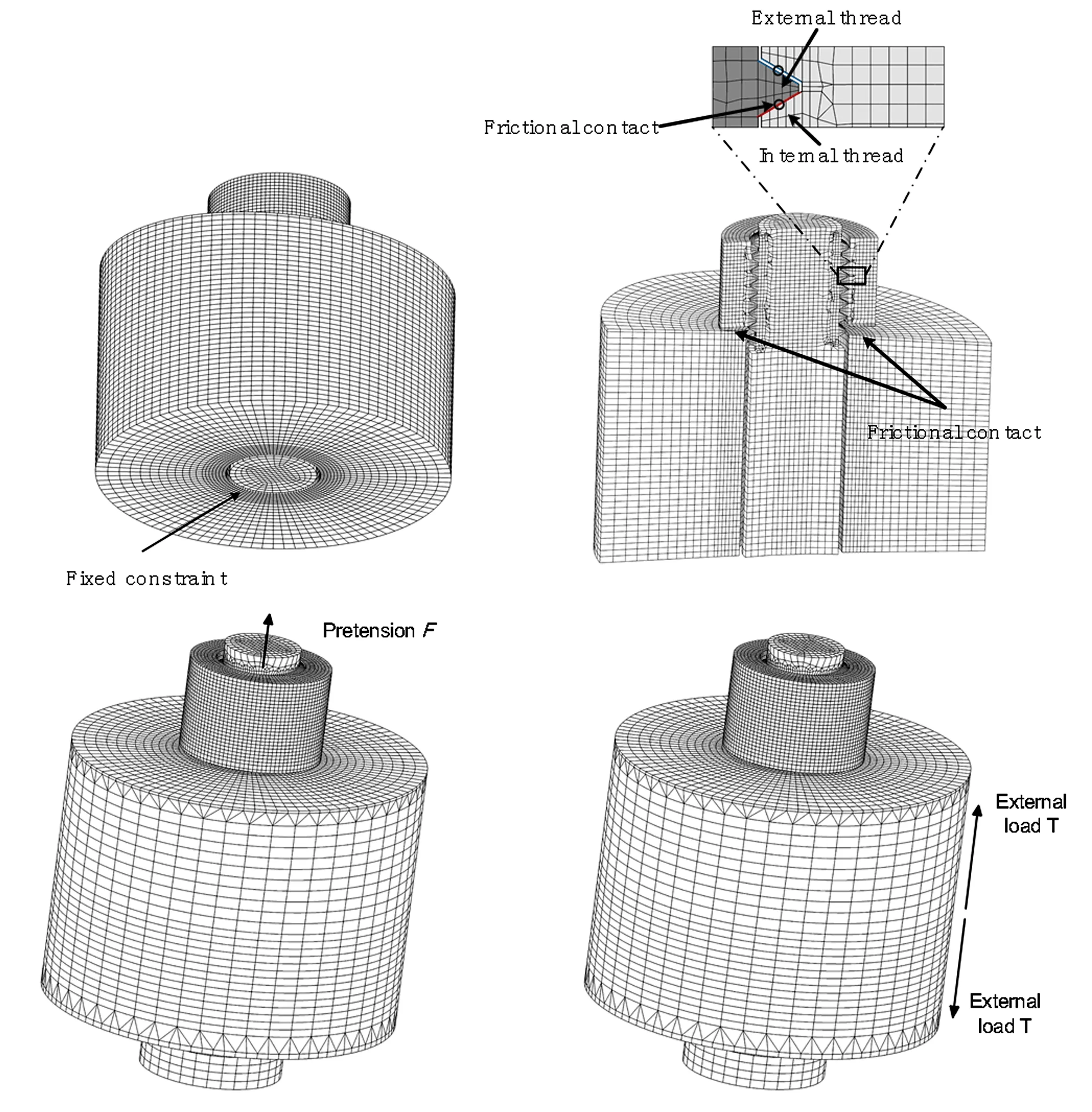
图2 螺栓连接结构有限元模型Fig.2 Finite element model of bolted joint

为了比较准确地分析出不平行度对螺栓连接刚度的影响,在划分网格时,通过手动控制网格,使螺栓端面与被连接件的支撑面的网格细化.网格划分采用solid186单元,其中,平行状态下模型共计124963个单元,447615个节点.模型中材料为镍基高温合金GH4169：弹性模量200GPa、泊松比0.3.模型中坐标系x轴为螺栓轴向.

在载荷施加方面,将拉伸载荷作用在螺栓连接部件的接触面上,是将螺栓看作拉伸弹簧,上下被连接件看作受压弹簧.拉力载荷的施加减小了上、下被连接件之间的作用力大小,而没有增加连接部件上的总载荷,并非部件完全受力,施加位移载荷同时增加了螺栓与节点部件的初始变形,让螺栓变长,被连接件进一步受压,所以计算螺栓连接刚度施加位移载荷较为合理.

在螺栓连接参数化有限元模型中,分步施加载荷.螺栓拧紧过程中,在螺杆上分步施加预紧力至30000N.拧紧完成后施加外载荷,上、下被连接件接触面施加0.01mm的x轴方向远端位移约束.第一载荷步为螺栓拧紧过程,第二载荷步为拉伸载荷施加过程,然后分别计算两个载荷步完成时的上、下两被连接件接触面的接触反力.

1.2 螺栓拧紧过程仿真分析结果

利用ANSYS WORKBENCH非线性算法计算不平行接触状态下各子步螺栓拧紧过程中被连接件的压缩量ΔL及对应预紧力值F,利用胡克定律F=k·x,计算出拧紧过程被连接件刚度,被连接件刚度表达式：

分别计算不平行角度θ为0°、0.8°、1.6°、2°下拧紧过程中各子步完成时的被连接件压缩量值及对应的预紧力值.图3 为预紧力施加30%、70%和100%时的拧紧过程应力云图,可见随着预紧力值的增加应力锥逐渐形成,预紧力值达到30%时,不平行度的影响已经显现,应力分布左右不均,应力集中现象产生,螺杆已经弯曲偏斜；预紧力值达到70%至拧紧完成时,应力集中现象明显,螺杆明显弯曲且应力锥偏心,随着不平行角度增大变化趋势更为剧烈.图4为不同平行度下被连接件的载荷-位移曲线,可见在拧紧过程中随着预紧力的增加,被连接件压缩量逐渐增大.曲线斜率变化较小,证明拧紧过程中被连接件刚度发生变化但是波动较小.随着不平行角度增大,曲线斜率下降表明被连接件刚度也在减小.

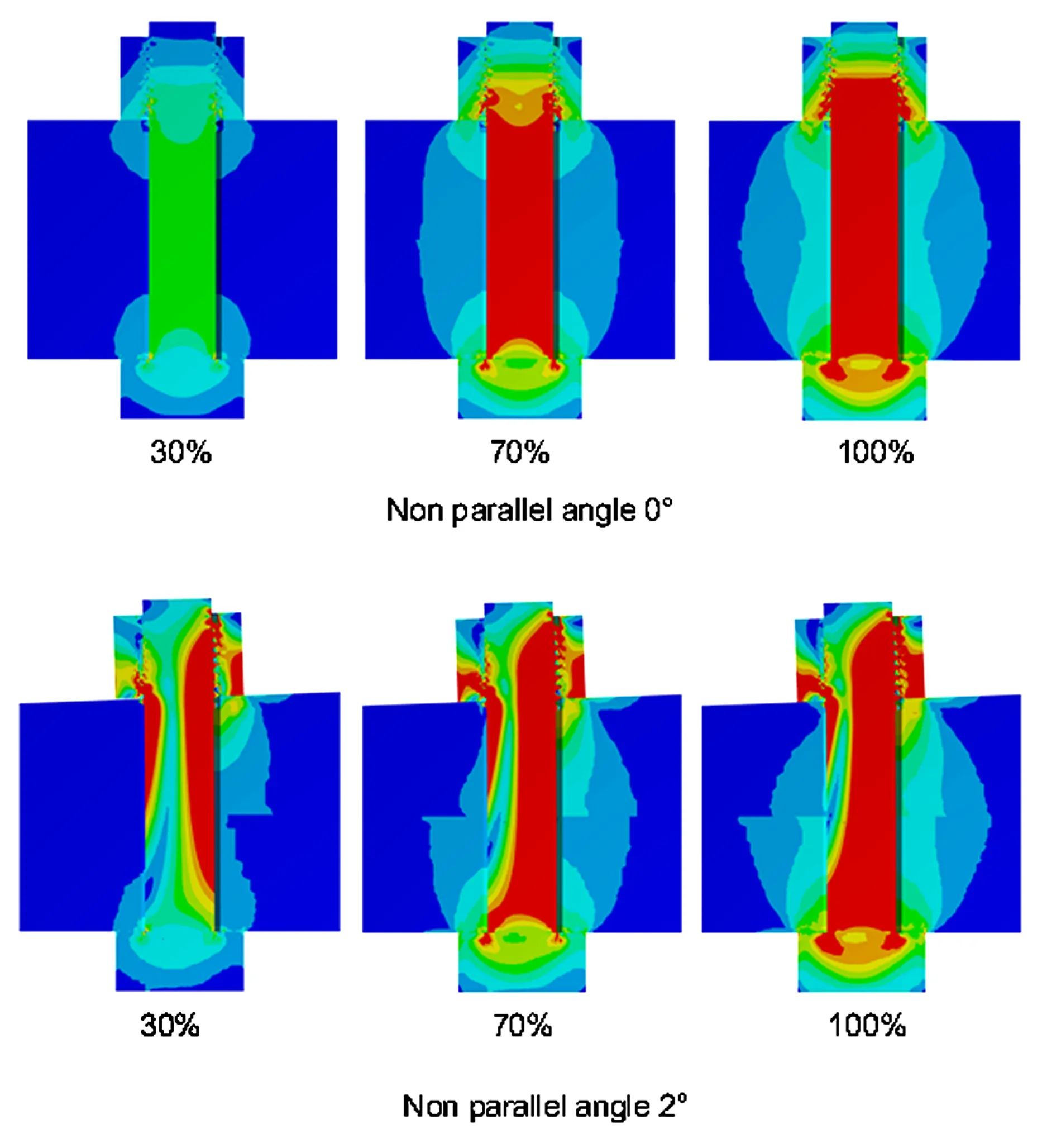
图3 不同平行度下的拧紧过程应力云图Fig.3 Contour figures of tightening process under different parallelism

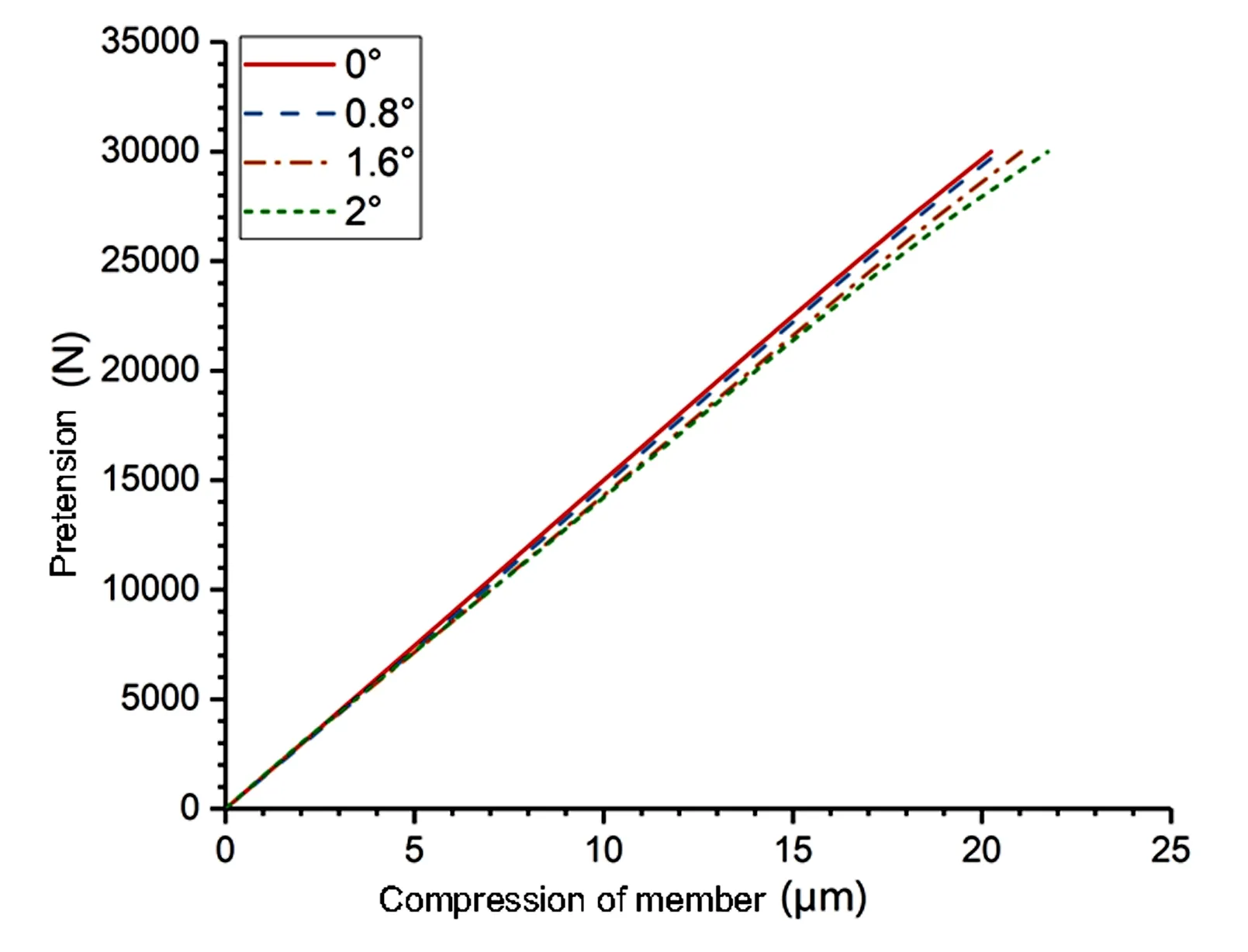
图4 不同平行度下的被连接件载荷-位移曲线Fig.4 Load-displacement curve of members under different parallelism

1.3 螺栓连接刚度仿真分析结果

利用ANSYS WORKBENCH非线性算法计算两个载荷步完成时上、下被连接件接触面的接触反力值FN1、FN2,利用胡克定律F=k·x,计算出螺栓连接刚度,螺栓连接刚度表达式：

X轴方向接触反力值FN1、FN2由有限元仿真计算得出,σ为接触面分离距离,这里取0.01mm.分别计算出不平行角度θ为0°、0.4°、0.8°、1.2°、1.6°、1.8°、2°时的螺栓连接刚度.不同角度下螺栓节点的刚度值见表1.

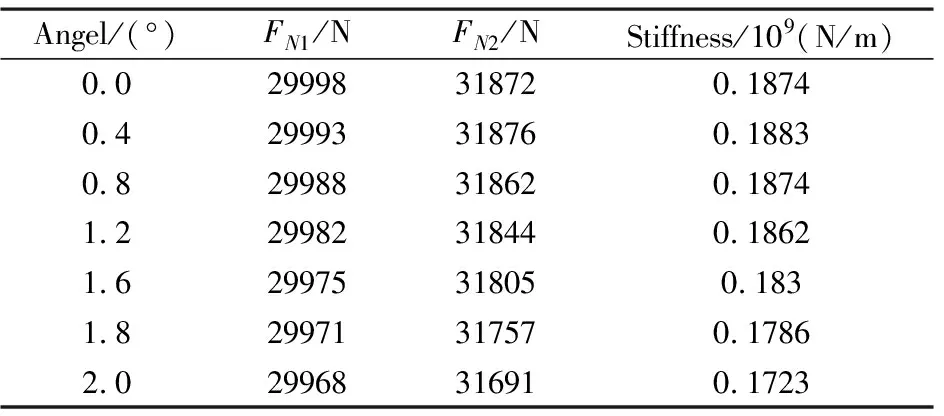
表1 不同平行度下螺栓连接刚度Table 1 Stiffness of bolt joint under different parallelism

不同平行角度下,螺栓连接刚度的计算分为两个载荷步,第一载荷步螺栓拧紧完成时,被连接件应力云图如图5所示.第二载荷步拉伸载荷施加完成时,螺栓连接部件应力云图如图6所示.从图中可以清晰看到平行状态下节点部件应力分布呈对称状圆锥体,这也与Motosh提出的等价中空截头圆锥体模型相符.不平行偏差对于应力分布影响较大,可以看到应力锥发生了明显的偏心形变,且有应力集中现象发生.不平行状态下螺栓张紧过程中,螺母会逐渐贴合被连接件端面,螺杆发生弯曲,部件中的各接触面将会传递弯矩,这些结构上的变化都是影响螺栓连接刚度的因素.

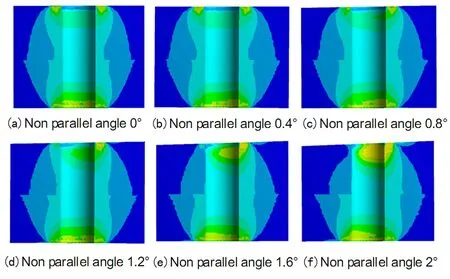
图5 不平行角度下拧紧状态被连接件应力云图Fig.5 Contour figures of members of tightening process under different parallelism

螺栓连接刚度随着不平行角度的增加呈先增后减状态,当不平行角度在0°～0.4°范围内变化时,连接刚度变化小于0.48%,增大趋势不明显,随着不平行角度继续增大连接刚度呈下降趋势且越来越剧烈,角度达到1.5°左右时,螺母与被连接件贴合状态转变为非完全接触,刚度值下降速度突然增大,当不平行度达到2°时,与平行状态相比连接刚度变化了8.1%.被连接件刚度随着不平行角度增加呈下降趋势且变化趋势越来越剧烈,如图7所示.

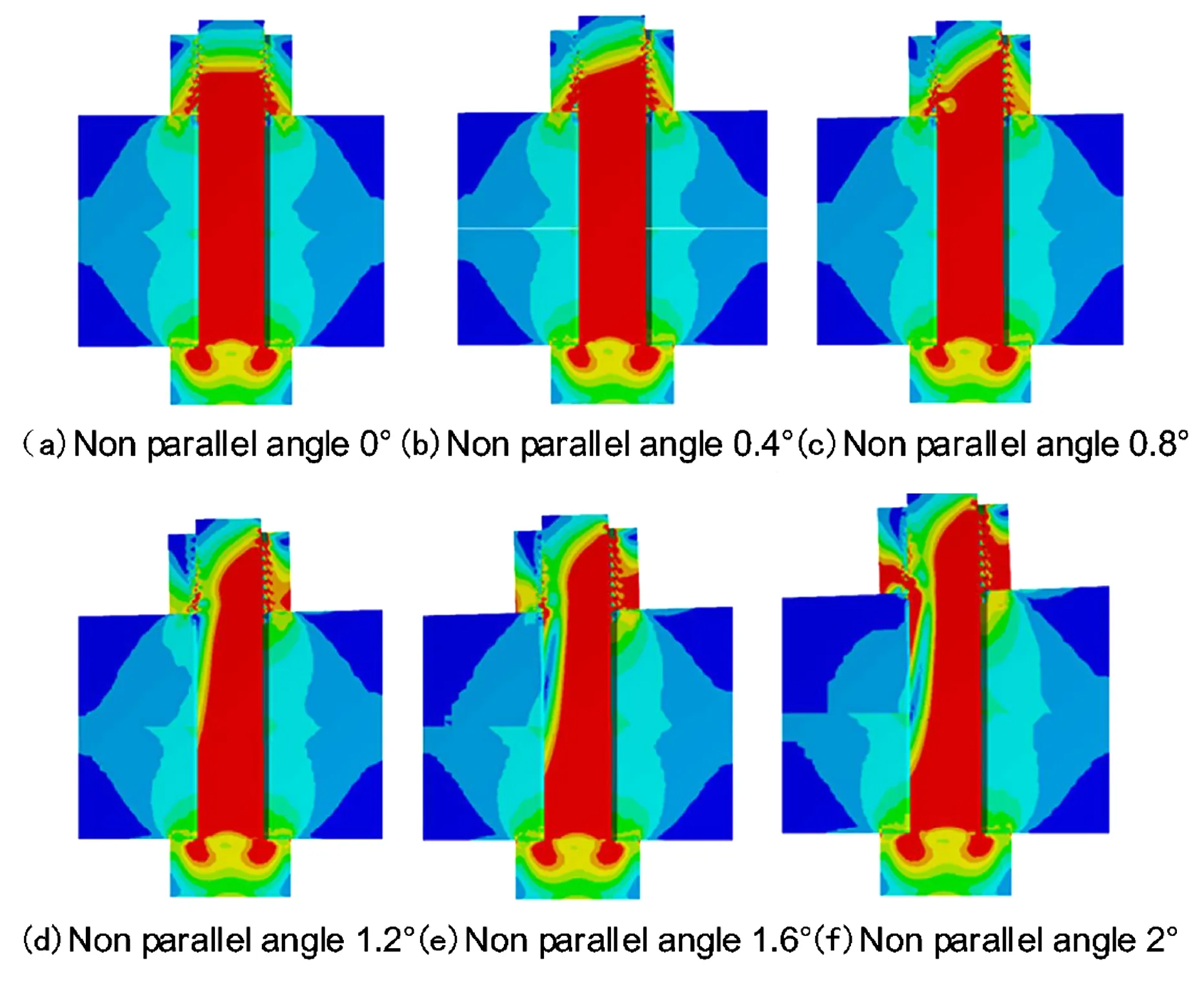
图6 不平行角度下拉伸状态螺栓部件应力云图Fig.6 Contour figures of bolted joints of stretching process under different parallelism

2 不平行接触下的转子模态仿真分析

2.1 有限元模型

为了分析由被连接件不平行接触导致的螺栓预紧力偏差对于法兰件动态特性的影响规律,建立模拟转子连接结构有限元模型.模型由一对安装边、8个M8螺栓螺母组成,如图8所示.为高效地分析出法兰件动态特性的变化规律,网格划分采用solide186单元,自动划分网格,控制网格尺寸为3mm.模型中被连接件材料为45#钢,螺栓材料为镍基高温合金GH4169.

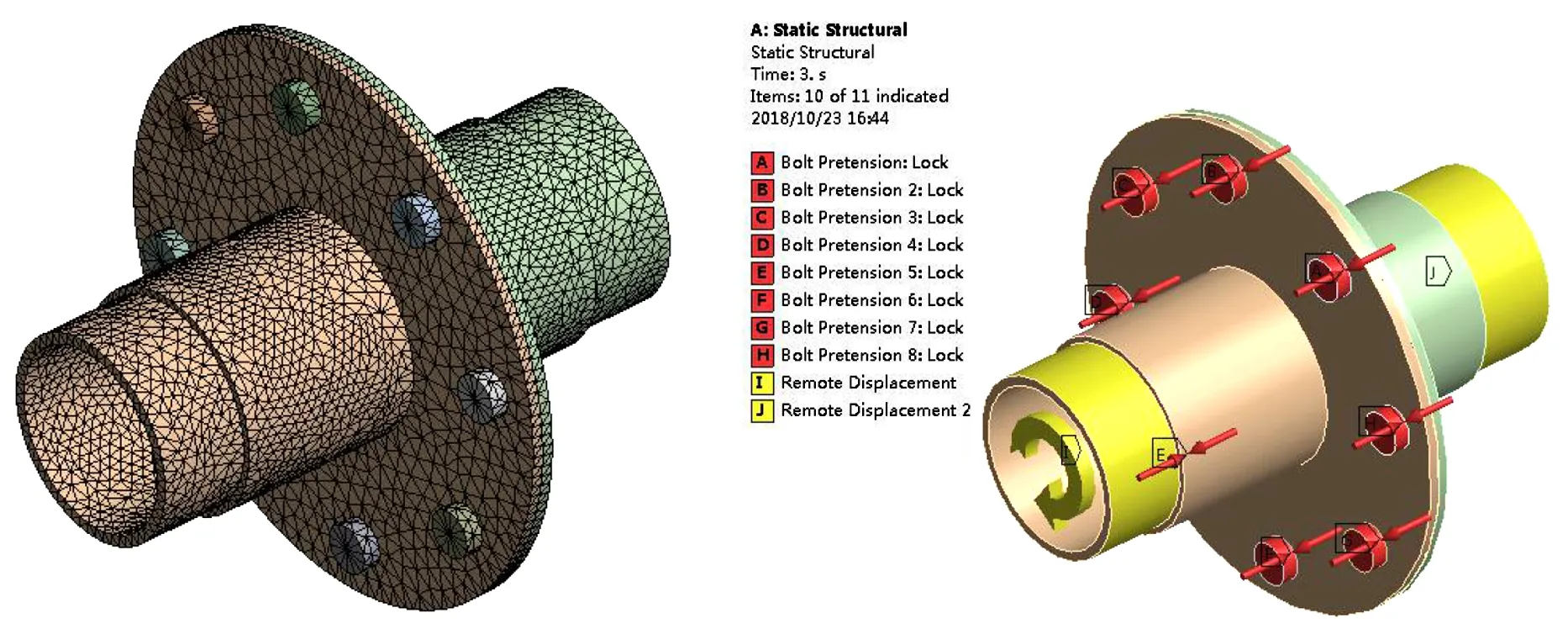
图8 模拟转子连接结构有限元模型Fig.8 Finite element model of rotor connection structure

在载荷施加方面,对螺杆施加预紧力,默认理想值为7500N.由于被连接件的不平行度存在会导致螺栓预紧力不均匀分布,故考虑上下20%的预紧偏差作用.1#～8#螺栓的值分别为6485、7920、8465、7085、7135、8236、6962和7069N(12点钟方向为1#螺栓,按逆时针排序).被连接件结合面之间设置为摩擦接触,摩擦系数定为0.2,其余设为绑定接触.应用圆柱面支撑模拟轴承支撑,采用远端位移约束,放开x轴的旋转自由度.运用ANSYS Workbench中的模态模块(Modal)进行静止态模态分析,不考虑刚化效应,不考虑旋转.先施加预紧力做静力学分析,导入模态分析,再进行带预应力的模态分析.

2.2 模态仿真分析结果

由于低阶模态对振动系统的影响较大,阶次越低,影响越大,阶次越高,误差越大,通常提取前5～10阶足够,但是对于不平行接触状态的装配体,具体到本文的模型仿真并不足以分析出整个系统的相应情况,因此提取转子系统前40阶固有频率和振型进行分析,频率结果见表2.前40阶次理想接触状态与不平行接触状态下转子固有频率的对比中,第35阶转子系统的固有频率变化值最大,达到91.5Hz；第31、32阶固有频率变化值也达到29.9Hz和20.7Hz,其余阶次变化不明显,动态特性较稳定.

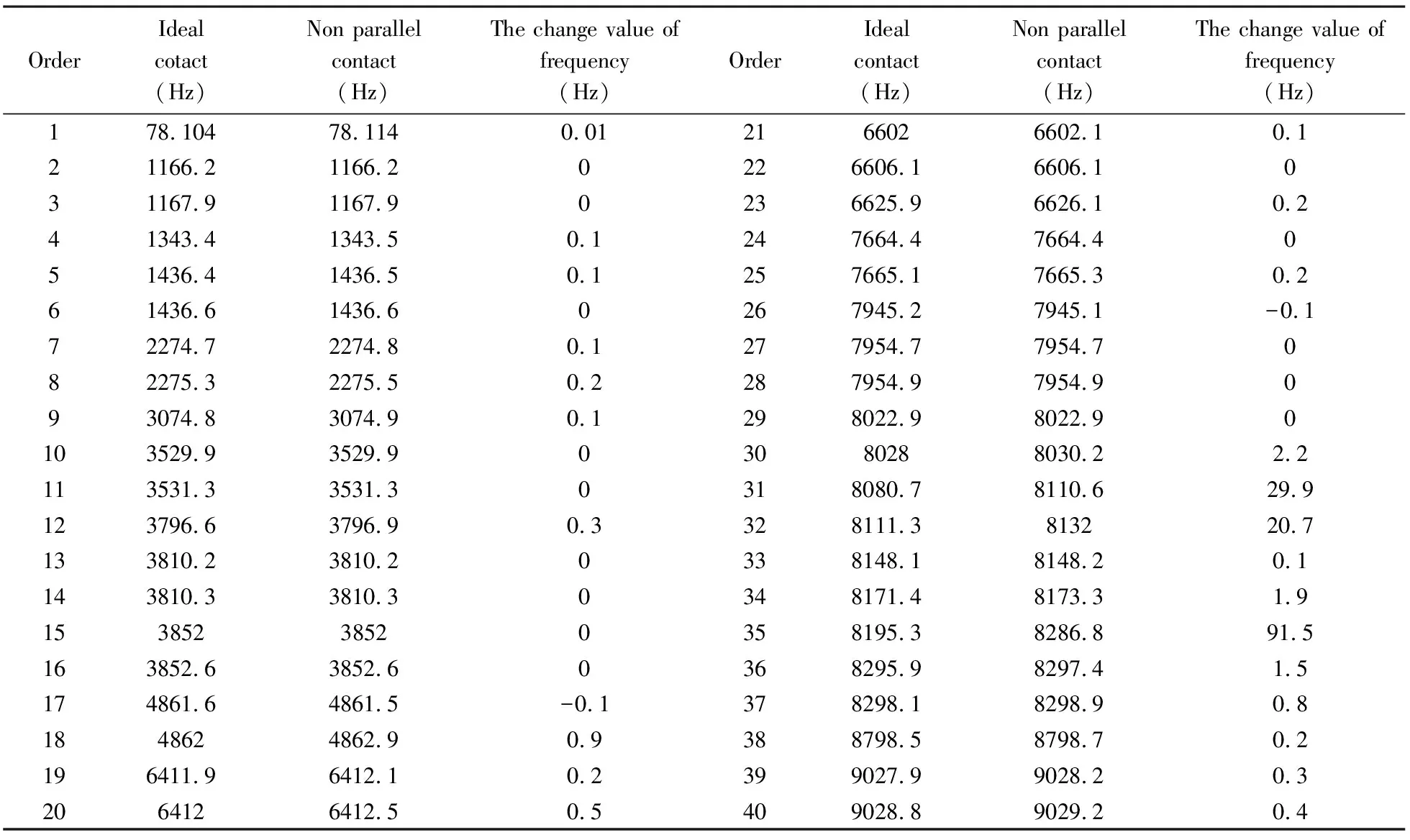
表2 转子系统固有频率Table 2 Natural frequency of rotor system

如图9所示为模拟转子连接结构低阶模态和敏感阶模态,对于低阶模态来说,其振型在理想接触和不平行接触下基本一致,这是因为低阶模态主要是对应转子的整体变形,与连接结构的整体刚度有关.不平行接触下的连接刚度非均匀分布虽然使得局部刚度产生变化,但对连接结构的整体刚度影响较小,因此对低阶模态的影响较小.对于高阶模态来说,其振型产生原因主要为螺栓间被连接件结合面的分离,由于各个螺栓附近的局部连接刚度的非均匀分布,导致各个螺栓间的振幅并不相同,同时,不同的敏感阶次下振型中最大振幅出现的位置也不相同.

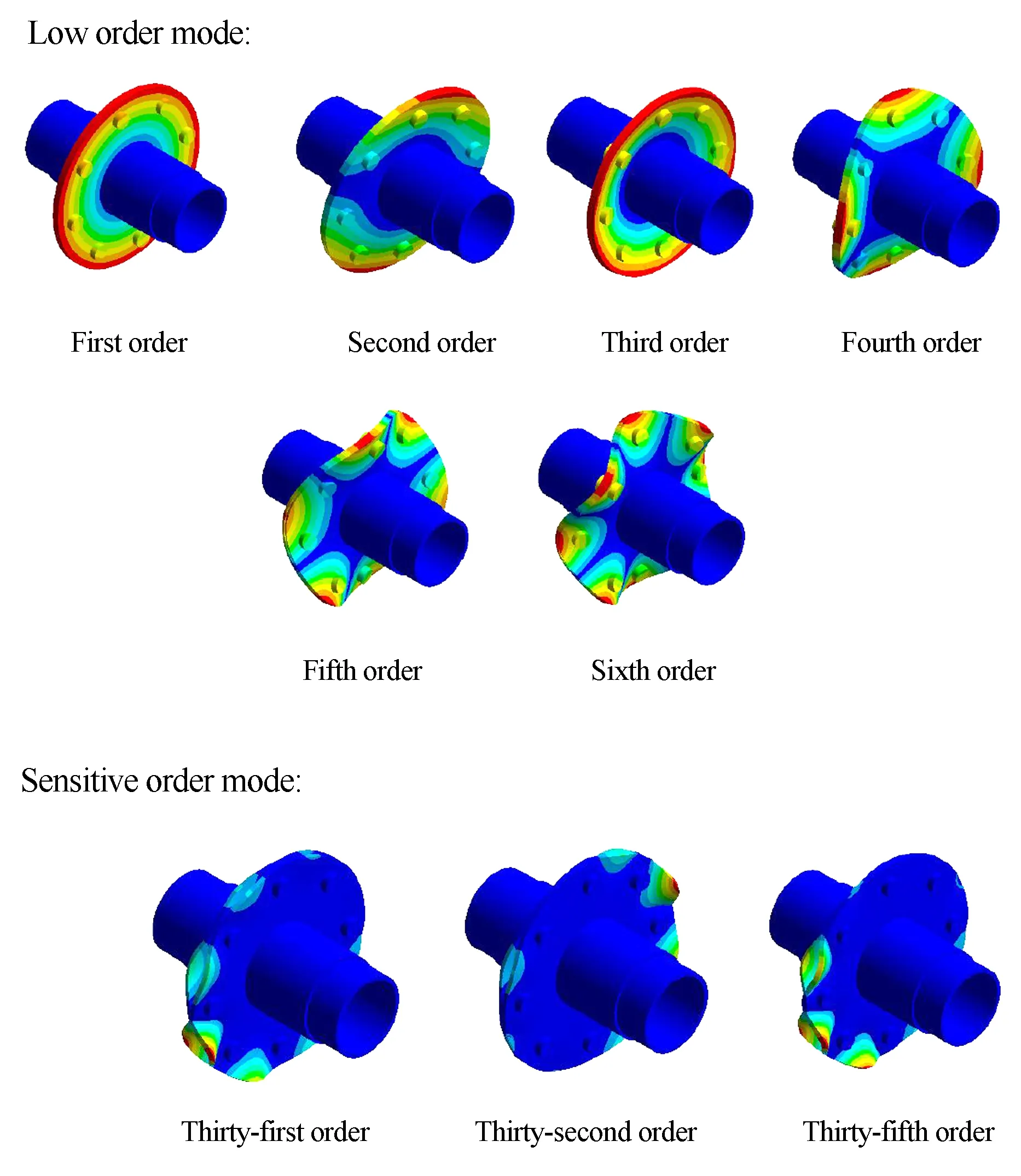
图9 模拟转子连接结构各阶次模态Fig.9 Various modes of simulation of rotor connection structure

3 总结

在螺栓的拧紧过程中,螺母会逐渐贴合被连接件端面,被连接件与螺母、螺栓端头接触部分应力集中明显尤其是螺杆弯曲方向一侧,平行状态下被连接件应力分布呈锥形分布,不平行接触状态下应力锥发生偏心形变且螺杆弯曲一侧变化明显,随角度增大其变形更为显著.

随着不平行角度的增加,被连接件刚度总体趋势为下降状态,达到某临界值后,螺母贴合状态转变为非完全接触,导致刚度值快速下降.在拉伸载荷施加阶段,随着不平行角度的增加,螺栓连接刚度的总体趋势也为下降状态且下降速度逐渐增大,结合面几何偏差的存在对螺栓连接刚度影响较为显著.

转子连接结构的不平行接触会引起局部连接刚度的非均匀分布,导致其动态特性发生变化,主要表现在某些高阶处的固有频率值发生很明显的变化,而较低阶固有频率基本不受不平行度的影响,敏感阶次的振型主要以螺栓间结合面的开合为主.