舰炮对岸区域射击最优表尺分配模型研究

卢发兴, 贾正荣, 吴 威

(海军工程大学电子工程学院,湖北 武汉 430033)

0 引 言

舰炮对岸射击作战任务中,岸上目标一般按照一定误差分布于一个范围内[1],为有效覆盖岸上目标,舰炮可以采用同距效力射、距离梯次效力射、方向梯次效力射、面积效力射等。在实施上述射击策略的过程中,需要解决的关键问题是表尺梯次差的求解以及射击弹丸数量的求解:包括求解距离表尺数、方向表尺数、距离梯次差、方向梯次差、射击弹丸总数量等参数。合理的舰炮对岸射击方案可以明显提高舰炮对岸射击的毁伤概率,同时节约射击弹丸消耗,具有重要军事意义[2-3]。

目前,在舰炮对岸射击方案问题的求解方法中。文献[4]分析了对岸上集群目标的舰炮对岸射击问题,给出了解析形式的舰炮对岸射击方案求解模型,但是其中射击弹丸数量的求解模型为经验模型,无法适应于多变的舰炮对岸射击题设。文献[5]分析了舰炮对海上集群小目标的毁伤问题,而在表尺梯次差求解过程中,该文献仍然采用了简化工程模型,方案还有进一步优化的空间。文献[6]分析了舰炮对岸射击表尺梯次差求取问题,给出了表尺梯次差问题的求解工程模型,该模型避免了对毁伤概率模型的优化分析,而是直接采用已有的优化问题求解方法进行数值求解。另外,该文献总结了舰炮对岸射击方案求解的流程,具有一定的工程实践意义。

综上,现有研究[4-8]对于舰炮对岸射击问题有了较为深入的认识,提出了多种用于表尺梯次差求解的方法,这些方法普遍认为表尺梯次差的最优求解具有较高的难度,因此避免以毁伤概率为指标直接对表尺梯次差进行优化求解,而是求取表尺梯次差的较优可行解。另外,在射击弹丸数量求解问题中,虽然根据文献[4-5]方法得到的结果能够满足毁伤概率要求,但是结果精度还有待提高。

本文分析舰炮对岸上集群目标的射击方案求解问题,直接以舰炮对岸射击毁伤概率为指标,通过变分法求解最优射击密度[9-12],基于该密度给出舰炮对岸射击方案,包括表尺梯次差求解及基于预定毁伤概率的射击弹丸数量求解。

1 舰炮对岸射击毁伤概率模型

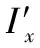
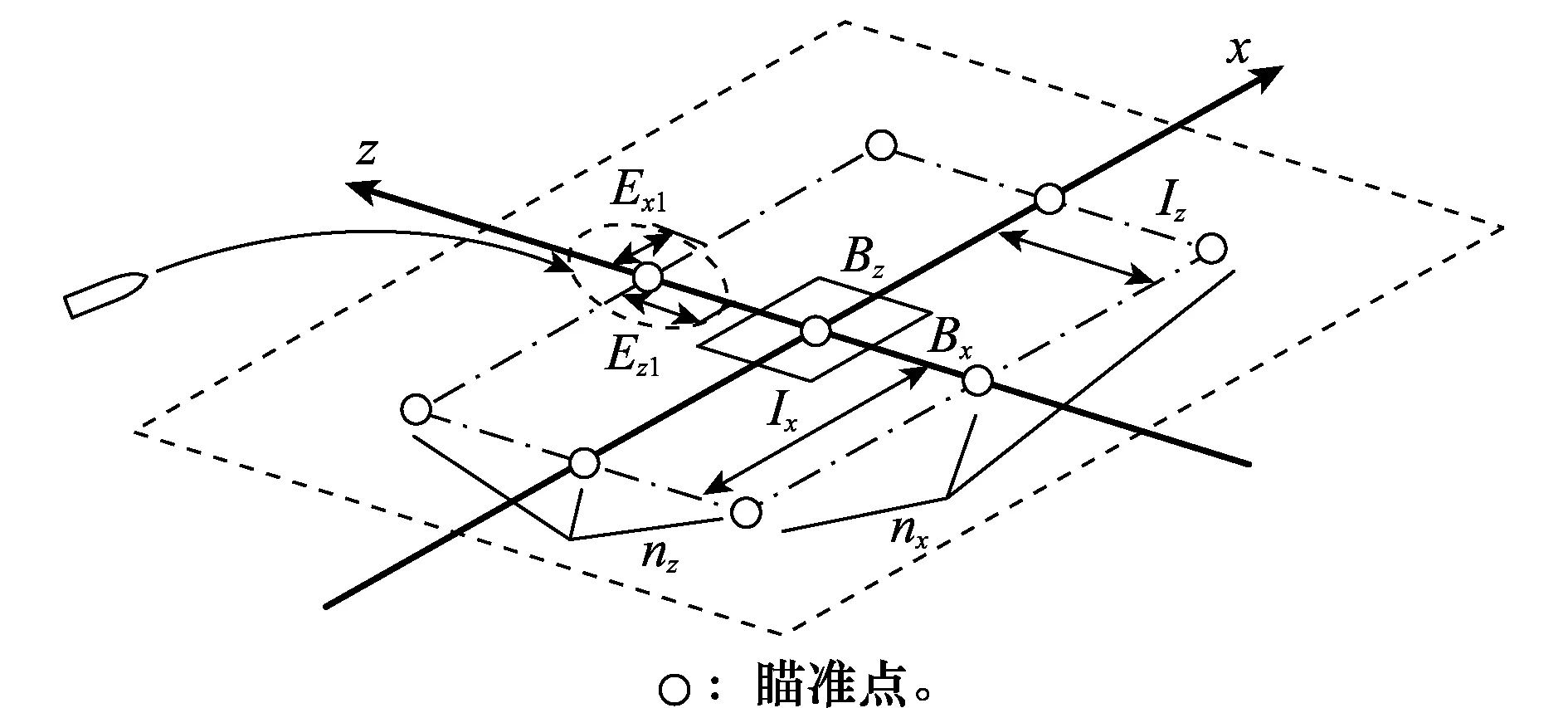
图1 舰炮对岸射击示意图Fig.1 Naval gunfire support against targets on land

设目标分布概率密度为f(x,z),则舰炮对岸射击毁伤概率模型为

(1)

式中,(xi,zj)为根据方向表尺数、距离表尺数及表尺梯次差得到的射击瞄准点等效坐标,即

(2)

p(x,z)为单发命中条件概率。

岸上集群目标可能服从不同的概率分布,当服从正态分布时,射击相关误差为Ex2与Ez2,归一化等效射击相关误差εx=Ex2/Ez1、εz=Ez2/Ez1,当目标服从均匀分布时,设目标散布区域为[-Lx,Lx]×[-Lz,Lz],归一化为[-lx,lx]×[-lz,lz]。

2 舰炮对岸射击最优中间函数

采用变分法,通过引入中间函数,可以直接以毁伤概率为指标求解毁伤概率的极值,即最优毁伤概率,而此时最优毁伤概率对应的中间函数为最优中间函数,该函数能够用于求解表尺梯次差。下面分别对目标服从正态分布以及目标服从均匀分布两种情况进行求解。

2.1 目标正态分布时的最优中间函数

引入中间函数Un(x,z):

(3)

通过变分求解[11-13],可以得到最优中间函数Un,o(x,z):

(4)

其中

(5)

式中,τn为

(6)

中间函数取最优时,可以解得最优毁伤概率为

(7)

目标正态分布时的最优毁伤概率Pn,o能够反映给定目标幅员、射击相关误差、不相关误差情况下舰炮对岸射击所能达到的毁伤概率上界,在实际求取舰炮对岸射击方案时,需要使用最优中间函数。

2.2 目标均匀分布时的最优中间函数

目标均匀分布时,仍然引入中间函数Ue(x,z),Ue(x,z)具有与Un(x,z)相同的形式,因而τe=τn。通过变分求解,可以得到目标均匀分布时的最优中间函数Ue,o(x,z)形式为

(8)

当中间函数取最优时,有目标均匀分布时的最优毁伤概率Pe,o为

(9)

3 表尺梯次差求解方法

结合第2节中的舰炮对岸射击最优射击密度,可以给出相应的表尺梯次差求解方法,下面分别针对目标服从正态分布与均匀分布两种情况进行分析。

3.1 目标正态分布时的表尺梯次差求解方法

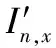
(10)

同理可得

(11)

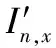
(12)

3.2 目标均匀分布时的表尺梯次差求解方法

(13)

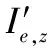
(14)

(15)

4 基于预定毁伤概率的射击弹丸数量求解

舰炮执行对岸射击作战任务时,一般需要在射前指定射击弹丸数量,射击弹丸数量与毁伤概率密切相关。由于执行作战任务一般会预先给出期望达到的毁伤概率,可以以此概率为基础,结合本文表尺梯次差求解方法,提出求解射击弹丸数量的方法,从而使实际毁伤概率达到预定要求。

4.1 射击弹丸数量求解思路

这里给出一种迭代方法求解射击弹丸数量。进行舰炮对岸射击时,射击瞄准点由距离表尺数nx、方向表尺数nz确定,向每个瞄准点发射h发炮弹,射击弹丸数量总数为n=nxnzh。

为方便射击指挥与实施,距离表尺数与方向表尺数一般为奇数,并且数值不超过某一常数。而当表尺数量超过这一常数时,则需要采用分段射击的方法。对于单个舰艇,通常取nx∈{1,3,5}以及nz∈{1,3,5}。当nx与nz固定时,改变射击弹丸数量n的参数为h。

对于每一种给定的(nx,nz),构建迭代序列hk,k∈N+,求解参数每个瞄准点发射的弹丸数量,其步骤[14-16]为:首先根据预定毁伤概率Pc求解得到射击弹丸数量初值h1,然后根据射击弹丸数量迭代函数ϑ(hk)求解后续hk+1。因此,射击弹丸数量求解的迭代方法可以表示为

(16)

迭代的终止条件为

(17)

式中,δ为允许的计算误差。

在进行舰炮对岸射击方案求解时,由于(nx,nz)的取值有限,即(nx,nz)∈{1,2,3}×{1,2,3},并且(nx,nz)≠(1,1),所以可以针对每一种(nx,nz)分别计算对应的h及n,选取其中所需射击弹丸数量n最小的舰炮对岸射击瞄准点(nx,nz)取值,即穷举求取最优方案。

下面根据目标不同的分布情况给出具体的初值计算函数、射击弹丸数量迭代函数的具体形式。

4.2 初值计算函数

(1) 目标正态分布

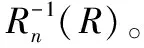
(18)

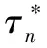
(19)

构建迭代[19]过程

(20)

即可得到满足要求的h。

(2) 目标均匀分布

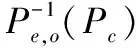
(21)

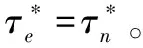
4.3 射击弹丸数量迭代函数

采用牛顿迭代法。给定(nx,nz),对于序列中的任意值hk,可以根据第3节中的方法求解得到表尺梯次差,进而求解得到对应的毁伤概率P(hk),从而可以构建射击弹丸数量迭代函数

(22)

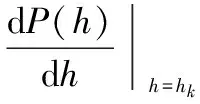
(23)

5 算例分析

为验证本文方法,分别进行典型算例的求解,与现有方法进行对比,以及在目标分布特性未知的情况下进行求解。

5.1 舰炮对岸射击方案求解流程

首先给出舰炮对岸射击方案的求解流程,如图2所示。

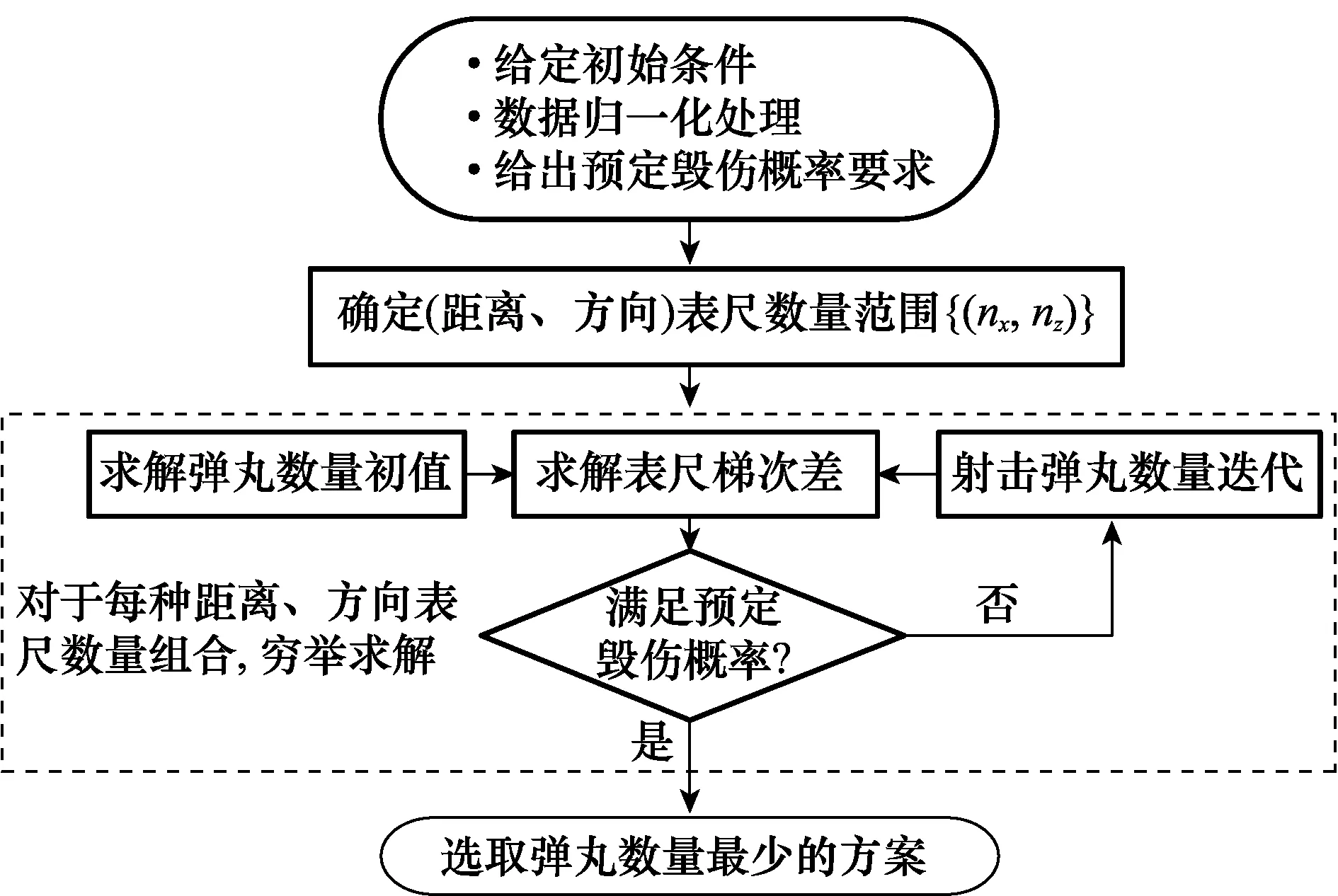
图2 舰炮对岸射击方案求解流程Fig.2 Flow chart of NGSTL plan solving

5.2 典型算例

对于目标散布服从正态分布与均匀分布两种情况,分别求解两种目标相关误差条件下的舰炮对岸射击方案。取预定毁伤概率Pc为0.450 0,最大表尺数不超过5个,射击不相关误差(Ex1,Ez1)、目标幅员(Bx,Bz)、毁伤目标所需弹药数量期望ω等条件如表1所示。

表1 算例初始条件

(1) 目标正态分布

相关误差(Ex2,Ez2)取值(90 m,36 m)与(40 m,25 m)时,得到计算结果如表2所示。

表2 舰炮对岸射击方案(目标正态分布)

(2) 目标均匀分布

目标散布区域特征(Lx,Lz)取值(216 m,130 m)与(120 m,60 m)时,得到的计算结果如表3所示。

表3 舰炮对岸射击方案(目标均匀分布)

根据表2和表3的计算结果,可以看出:对于不同的方向和距离表尺数,本文方法计算得到的表尺梯次差及射击弹丸数量都能够满足预定毁伤概率的要求。

5.3 与现有方法对比

文献[4]给出了完整的表尺梯次差求解方法及弹药消耗量计算方法,但是并没有计算舰炮对岸射击方案对应的毁伤概率,现将文献[4]中的方法与本文方法进行对比。

文献[4]中以舰炮对岸上集群目标射击为例,设定预定毁伤概率为0.225,并计算了具体的表尺距离梯次差、方向梯次差与弹药消耗量,计算初始条件如表4所示。

表4 算例初始条件(对比)

文献[4]针对该例计算得到了舰炮对岸射击方案,(由于283不能被9整除,因而增加射击弹丸数量至288发,从而有h取32)。根据该方案,通过式(1)计算毁伤概率,结果如表5所示。

表5 现有方法舰炮对岸射击方案

在相同预定毁伤概率要求(0.225)下,采用本文方法,得到的舰炮对岸射击方案如表6所示。

表6 本文方法舰炮对岸射击方案

可见,采用本文方法,方向表尺数与距离表尺数取(3,3)时,只需要72发弹丸即可达到毁伤概率0.226 1,相比文献[4]的方法减少了211发,能精确地满足0.225的毁伤概率要求；而当方向表尺数与距离表尺数取(5,5)时,需要225发弹丸即可达到毁伤概率0.470 7,相比于文献[4]中方法,射击弹丸数量减少了58发,方法的优化程度更高。

5.4 目标分布特性未知的情况

实战中可能无法确定目标分布特性,因而需要对目标分布特性进行一定的假设。一般而言,均匀分布是一种较为恶劣的分布情况,可以假设目标服从均匀分布求解舰炮对岸射击方案。

设目标实际服从正态分布,并且进行方案求解时目标分布特性未知。因此,假设目标服从均匀分布,根据目标相关误差进行舰炮对岸射击方案的求解,对于得到的方案,计算该方案在目标实际分布特性(正态分布)下的毁伤概率。

设相关误差为(Ex2,Ez2),根据相关误差得到均匀分布假设条件下等效的目标散布区域,有

(24)

根据式(24)等效后,有

(25)

即在散布区域[-Lx,Lx]×[-Lz,Lz]内,目标实际的散布概率(正态分布)与假设条件(均匀分布)的散布概率几乎相等。

采用第5.1节中的题设,(Lx,Lz)取(120,60),得到目标均匀分布假设下的毁伤概率Pe,并计算目标实际分布(正态分布)下的毁伤概率Pn,结果如表7所示。

表7 均匀分布假设条件下的舰炮对岸射击方案对比

为对比达到同等毁伤概率所需的射击弹丸数量,分别取预定毁伤概率为0.670 0与0.450 0,计算已知目标正态分布条件下的舰炮对岸射击方案,如表8所示。

表8 已知正态分布条件下舰炮对岸射击方案对比

由表7和表8可得:

(1) 假设目标服从均匀分布,求解舰炮对岸射击方案,得到的方案对于目标实际服从正态分布的情况,都能够得到高于预定要求的毁伤概率,因此假设目标均匀分布在战术上是可行的；

(2) 相比于已知目标服从正态分布的情况,假设目标服从均匀分布时,达到相同的毁伤概率所需的射击弹丸数量更多,即均匀分布是一种较为恶劣的目标分布情况。

因此,在实际应用中,当无法确定目标分布特性时,可以假设目标服从均匀分布并求解舰炮对岸射击方案。虽然这样做会增大射击弹丸消耗,但是可以保证毁伤概率达到预定要求。

6 结束语

舰炮能够提供快速的对岸火力压制,充分发挥舰炮这一优势,需要结合区域射击方法具体分析并优化表尺梯次差、射击弹丸数量求解方法。本文提出了包含表尺梯次差求解及射击弹丸数量求解在内的舰炮对岸射击方案求解模型,流程简洁,结果准确,相比于现有方法在优化程度方面有一定提升,能够为对岸射击指挥提供更好的辅助决策。

[1] ROB B M. Naval gunfire support to amphibious operations across the spectrum of conflict[R]. Fort Leavenworth, Kansas: United States Army Command and General Staff College, 1998.

[2] RENE T. Raising the IOWA: reactivating the iowa class battleships to fill the current naval surface fire support vacancy[R]. Quantico, VA: Marine Corps University, 2009.

[3] AMY E. Integrating naval surface fire support into an improved joint close air support architecture[R]. Monterey, CA: Naval Postgraduate School, 2006.

[4] 邵鹏举, 潘红华, 王志民. 舰炮对岸应召射击最优火力分配[J]. 指挥控制与仿真, 2008, 30(5): 40-46.

SHAO P J, PAN H H, WANG Z M. Optimal firing distribution of navy gun’s surface-to-shore calling fire[J]. Command Control & Simulation, 2008, 30(5): 40-46.

[5] 田峰,白江,孙续文.舰炮对海上集群小目标射击的毁伤概率[J].指挥控制与仿真,2013,35(1):62-66.

TIAN F, BAI J, SUN X W. Research on the damage probability of group small targets at sea of naval gun firing[J]. Command Control & Simulation, 2013, 35(1): 62-66.

[6] 汪德虎,关庆云.编队舰炮对岸破坏射击标尺分配实用优化[J].舰船电子工程,2009,29(11):66-69.

WANG D H, GUAN Q Y. Applied optimization of destroy firing’s backsight distribution in the formation-guns fire to the shore[J]. Ship Electronic Engineering, 2009,29(11): 66-69.

[7] 王连柱,王龙涛,申战胜.空域窗射击舰炮火力分布方法[J].指挥控制与仿真,2016,38(3):97-107.

WANG L Z, WANG L T, SHEN Z S. Firing distribution method for naval gun to shoot at future airspace window[J]. Command Control & Simulation, 2016, 38(3): 97-107.

[8] 邱志明, 曹渊, 郭勇. 舰炮武器对岛礁上集群目标射击效力指标算法研究[J]. 兵工学报, 2016, 37(1): 37-41.

QIU Z M, CAO Y, GUO Y. Research on the algorithm for firing efficiency of naval gun weapon system against group targets on island[J]. Acta Armamentarii, 2016, 37(1): 37-41.

[9] 卢发兴,贾正荣,吴玲,等.未来空域窗弹丸瞄准点配置方法[J].兵工学报,2015,36(8):1541-1545.

LU F X, JIA Z R, WU L, et al. Configuration method of aiming points for Future Airspace Window[J]. Acta Armamentarii, 2015, 36(8): 1541-1545.

[10] 卢发兴,贾正荣,吴玲,等.最优未来空域窗模型[J]. 系统工程与电子技术, 2015, 37(5): 1072-1075.

LU F X, JIA Z R, WU L, et al. Optimal model of future airspace window[J]. Systems Engineering and Electronics, 2015, 37(5): 1072-1075.

[11] KOUIBIA A, PASADAS M. Optimization of the parameters of surfaces by interpolating variational bicubic splines[J]. Mathematics & Computers in Simulation, 2014, 102(4): 76-89.

[12] MORDUKHOVICH B S, SARABI M E. Stability analysis for composite optimization problems and parametric variational systems[J]. Journal of Optimization Theory & Applications, 2016: 1-24.

[13] KE Y, MA C. Iterative algorithm of common solutions for a constrained convex minimization problem, a quasi-variational inclusion problem and the fixed point problem of a strictly pseudo-contractive mapping[J]. Fixed Point Theory & Applications, 2014, 2014(1):1-15.

[14] ÉSIK Z, RONDOGIANNIS P. A fixed point theorem for non-monotonic functions[J]. Theoretical Computer Science, 2015, 574: 18-38.

[15] KIRKBY R. Convergence of discretized value function iteration[J]. Computational Economics, 2015, 49:1-37.

[16] CHANG S H. Convergence of variational iteration method applied to two-point diffusion problems[J]. Applied Mathematical Modelling, 2016, 40(15/16):6805-6810.

[17] CHIDUME C E, OKPALA M E. Fixed point iteration for a countable family of multi-valued strictly pseudo-contractive-type mappings[J]. Springerplus, 2015, 4(1):1-12.

[18] GANG E K. Strong convergence for an implicit iteration process in Hilbert spaces[J]. Applied Mathematics & Computation, 2014, 239(2): 434-437.

[19] NAKAO M T. A numerical verification method for nonlinear functional equations based on infinite-dimensional Newton-like iteration[M]. Elsevier Science Inc. 2016.