基于HHT的高频雷达机动目标参数估计

张冰瑞, 雷志勇, 周海峰, 周 毅

(中国电子科技集团公司第十四研究所, 江苏 南京 210039)

0 引 言

高频雷达工作频段在3～30 MHz,具有超视距、覆盖范围大、性价比高的独特优势,在反走私稽查、电离层环境监测、早期战略预警、隐形飞机探测等多个领域具有重要的民用和军事价值[1-3]。高频雷达通过长时间相干积累增加目标信噪比,对于高速机动的飞机或导弹目标,多次回波中其运动状态变化较大,导致目标多普勒扩展影响能量聚集[4-6]。对这类机动目标的检测,需要通过一定手段进行运动补偿来提高检测效率,如何估计目标运动参数是其中的关键技术,逐渐成为该领域的研究热点。

目前的研究中,机动目标参数估计主要根据回波信号的相位信息,通过建立相应数学模型,利用不同数学工具对其进行解析和估计,从而获得目标速度和加速度等信息。常用算法有多通道补偿法[7]、多项式相位法[8-10]和基于时频分析技术[11-13]等算法。多通道补偿法将目标近似为匀加速运动,取若干加速度值分别对回波进行相位补偿,根据不同补偿通道的信噪比改善效果估计出目标加速度。文献[7]提出的多通道补偿算法综合应用了频率校正、通道合成和峰值检测,具有计算复杂度和虚警率低的优势。然而此类算法近似为穷举法,受实际通道数的限制难以实现目标运动参数的高精度估计。多项式相位法利用多项式为目标相位建模,通过高阶模糊函数估计出多项式的各阶系数,进而获得运动参数估计。文献[8]提出的方法通过高阶模糊函数估计出目标的高阶运动参数,并在回波中补偿掉该阶分量,循环执行直到目标所有运动分量都补偿掉,以此来估计各阶运动参数。该类方法计算量小、精度高,但对信噪比要求较高,在强杂波和多目标的情况下稳定性差。基于时频分析的方法将目标信号变换到时频域,通过时频域的能量积累进行目标参数估计。文献[11]提出的时频分析技术通过构造时间-频率变化率的联合域,并沿时间轴的不同直线路径进行积分来估计目标参数,在低信噪比下取得了较好效果。由于高频雷达地海杂波能量较大(通常比目标大10～50 dB),常规时频分析方法均需先利用海杂波循环对消法[14]和奇异值分解法[15-16]等抑制杂波,不仅增加了算法的运算量而且参数估计精度受制于杂波抑制效果的影响。同时,高频雷达距离分辨率低,经常会遇到同一距离单元存在多个目标的场景,常规算法需要逐个目标进行参数估计、加速度补偿和目标剔除的循环操作,导致运算量大且算法稳定性差。

针对现有算法存在的问题,本文研究基于希尔伯特黄变换(Hilbert-Huang transform,HHT)的机动目标运动参数估计方法,HHT是文献[17]提出的时频分析方法,该算法是数据驱动的自适应信号分析方法,能够很好地处理非平稳和非线性信号。经验模态分解(empirical mode decomposition,EMD)是其核心算法,通过将信号从时域分解为若干本征模态函数(intrinsic mode function,IMF)分量之和,每个IMF分量具有不同的时频特性,并利用希尔伯特变换计算出每个IMF分量的瞬时频率,从而获得信号的时频分布特性。为便于分析雷达信号,将EMD扩展到复数域,提出了复数经验模态分解(complex empirical mode decomposition, CEMD)方法[18-20]。本文将其用于高频雷达的机动目标参数估计,运用CEMD将目标慢时间维信号分解为多个IMF分量,根据目标和杂波的时频特性将其分解为不同的IMF分量,利用目标瞬时多普勒频率的变化特性,通过线性拟合估计出目标运动参数。与常规机动目标参数估计方法相比,该方法无需抑制杂波,可同时对多目标进行参数估计,数据分析结果表明该方法可以有效应用于目标参数估计。

1 希尔伯特黄变换

HHT包括2个阶段:第一阶段为 EMD,将信号按照一定规则自适应地分解成若干IMF分量;第二阶段为Hilbert谱分析,即获得每个IMF分量的瞬时频率和能量随时间的分布。CEMD方法借助了“旋转”这一概念,将复数信号描述为快速旋转IMF分量和慢速旋转IMF分量的叠加,通过计算复信号s(t)在不同旋转方向φn上的投影s'(t)[18],即

s'(t)=Re[s(t)e-iφnt]

(1)

φn=2nπ/N,n=1,2,…,N

(2)

将各旋转方向上投影包络的均值作为复信号包络(即慢速旋转分量),通过多次迭代从而将快速旋转分量提取出来。CEMD算法的详细流程如图1所示,其中复数IMF分量需满足2个条件:①在任意旋转方向φn上,复信号投影分量实部的零点与极值点相等或至多相差一个;②任意时刻,复信号在所有旋转方向上的投影分量确定的切线均值为零。

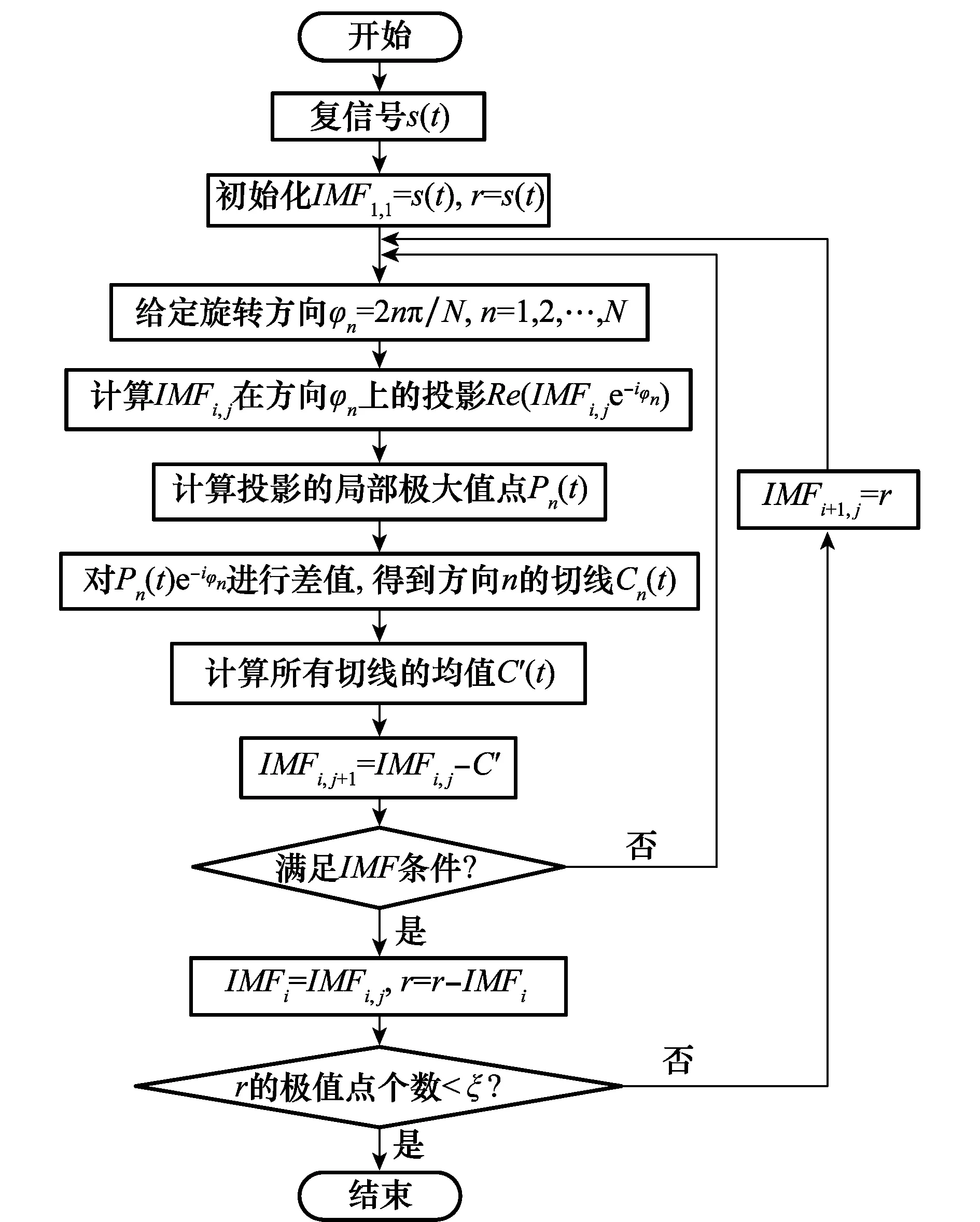
图1 CEMD算法流程图Fig.1 Flowchart of CEMD algorithm

传统傅里叶变换中,频率的定义主要针对平稳信号而言,即在时域上具有恒定幅度和频率的正弦或余弦函数。频率被定义为整个信号长度中具有恒定幅度的正弦或者余弦函数。而对于非平稳信号,频率是随时间不断变换的,因此用瞬时频率来描述更为合适。复数信号经过CEMD分解为若干单频(或窄带)瞬态信号A(t)ejω(t),瞬时频率定义为

(3)

其中

(4)

此时原信号s(t)可表示为时间、频率和幅度的函数，即若干IMF分量之和的形式为

(5)

式中，IMFi为第i个IMF分量；r为分解余量；fi(t)和Ai(t)分别为第i个IMF分量的瞬时频率和幅度。将其表示在时频平面上便得到s(t)的HHT时频谱H(f,t)。

2 机动目标模型及参数估计方法

高频雷达慢时间维回波信号s(t)的模型可表示为

s(t)=x(t)+c(t)+w(t)

(6)

式中,x(t)为目标信号;c(t)为地海杂波;w(t)为噪声。当高频雷达照射海上目标时,回波中就含有大量海杂波,回波频谱中海杂波在一阶Bragg峰fb处有很强的能量,其模型可以表示为[1]

(7)

式中,f0为雷达载频；θ为电磁波相对于海平面的入射角。机动目标速度模型可用n阶多项式表示为

v(t)=v0+a1t+…+antn

(8)

式中,v0为目标初始速度;an为n阶加速度。雷达机动目标检测中通常只需补偿一阶加速度[6],此时回波信号模型可表示为

x(t)=ej4π/λ(v0t+0.5a1t2)

(9)

高频雷达中根据杂波和目标的不同频谱特性,可采用CEMD算法将目标回波从杂波中分解出来,进而计算出目标时频谱,根据目标瞬时多普勒频率与时间的线性关系拟合出运动参数。具体步骤如下。

步骤1雷达在某一方位和距离单元上的慢时间维回波信号为S={s(1),s(2),…,s(N)},N为相干积累点数。采用CEMD对回波S进行分解,可得到若干IMF分量。

步骤2为抑制CEMD分解中的端点效应,即信号两端极值点的不确定导致的信号包络线拟合偏差,这里采用镜像延拓法[21-22]以靠近端点处的极值点为对称轴,将原始信号映射成一个周期信号,从而尽可能消除端点的影响。

步骤3合理的CEMD分解停止原则也是算法的关键。本文采用仿柯西收敛准则控制EMD的分解次数,即两个连续IMF的标准差SD小于一定阈值时判定分解过程结束[23]。

(10)

步骤4计算IMF分量的瞬时频率和幅度,获得目标HHT的时频谱,采用最小二乘法对瞬时频率随时间的变化曲线进行多项式拟合,获得目标初速度和加速度的估计。

3 算法性能分析

3.1 单目标场景

对高频雷达某一距离单元的慢时间维数据进行HHT算法处理,距离-多普勒谱如图2所示。

图2 回波信号距离-多普勒谱Fig.2 Distance-doppler spectrum of the echo signal

由图2可知，数据中加入一初始速度v0=100 m/s、加速度a1=30 m/s2的目标,目标信噪比20 dB,杂噪比47 dB。

信号时域图和频域图如图3所示,虽然目标能量较强,但由于目标加速度大,频谱展宽严重,采用常规CFAR检测困难。利用HHT算法对信号进行处理。首先对原始信号进行CEMD计算,形成2个IMF分量和1个剩余项，如图3所示。

图3 单目标CEMD计算结果Fig.3 CEMD results of the single target

由图3(a)中信号实部的时域波形可知,IMF分量的波动速率从大到小逐步降低,对这些信号做FFT;由图3(b)频谱图可知，原始回波是海杂波、目标和噪声成分的叠加。CEMD处理后第1个IMF分量主要为目标分量,第2个IMF分量和剩余信号主要为海杂波分量,而噪声存在于所有信号成分中,可见CEMD有效地将目标和杂波分离开来。

计算第1个IMF分量的瞬时频率和幅度,绘制成HHT时频谱如图4所示。图中用颜色变化表示瞬时频率随时间的分布情况,红色曲线为采用最小二乘法线性拟合的结果。

图4 单目标HHT时频谱Fig.4 HHT Spectrum of the single target

图5 单目标Dechirp计算结果Fig.5 Dechirp results of the single target

为研究算法鲁棒性,分析信噪比大小对目标速度和加速度估计精度的影响,在100个不同距离单元回波中加入不同信噪比的目标信号,计算HHT算法对目标速度和加速度的估计误差,并对100次计算结果取平均,获得统计结果如图6所示。

图6 不同信噪比下单目标参数的估计误差Fig.6 Estimation errors of single target parameters under different SNRs

由图6可知，Dechirp算法受制于SVD抑制海杂波的性能,低信噪比下速度和加速估计误差较大;采用HHT算法时,随着目标信噪比的增大,速度和加速估计误差呈快速减小的趋势,当信噪比大于13 dB时,两种方法的参数估计误差均小于1%。

3.2 多目标场景

考虑到高频雷达距离分辨率低,经常会遇到同一距离单元存在多个目标的情况,下面对多目标场景下的算法性能进行分析。在回波数据中加入初始速度100 m/s、加速度30 m/s2的目标1,同时加入速度80 m/s、加速度0 m/s2的目标2,两目标信噪比均为20 dB,对该场景下的数据进行HHT分析,结果如图7所示。

图7 多目标CEMD计算结果Fig.7 CEMD result of multi-targets

由图7可知,原始信号为海杂波、目标1、目标2和噪声的叠加,经CEMD处理信号被分解为3个IMF分量和1个剩余项,第1个IMF分量主要为目标1回波,第2个IMF分量主要为目标2回波,第3个IMF分量和剩余项主要为杂波。

第1个IMF分量的HHT时频谱如图8所示。

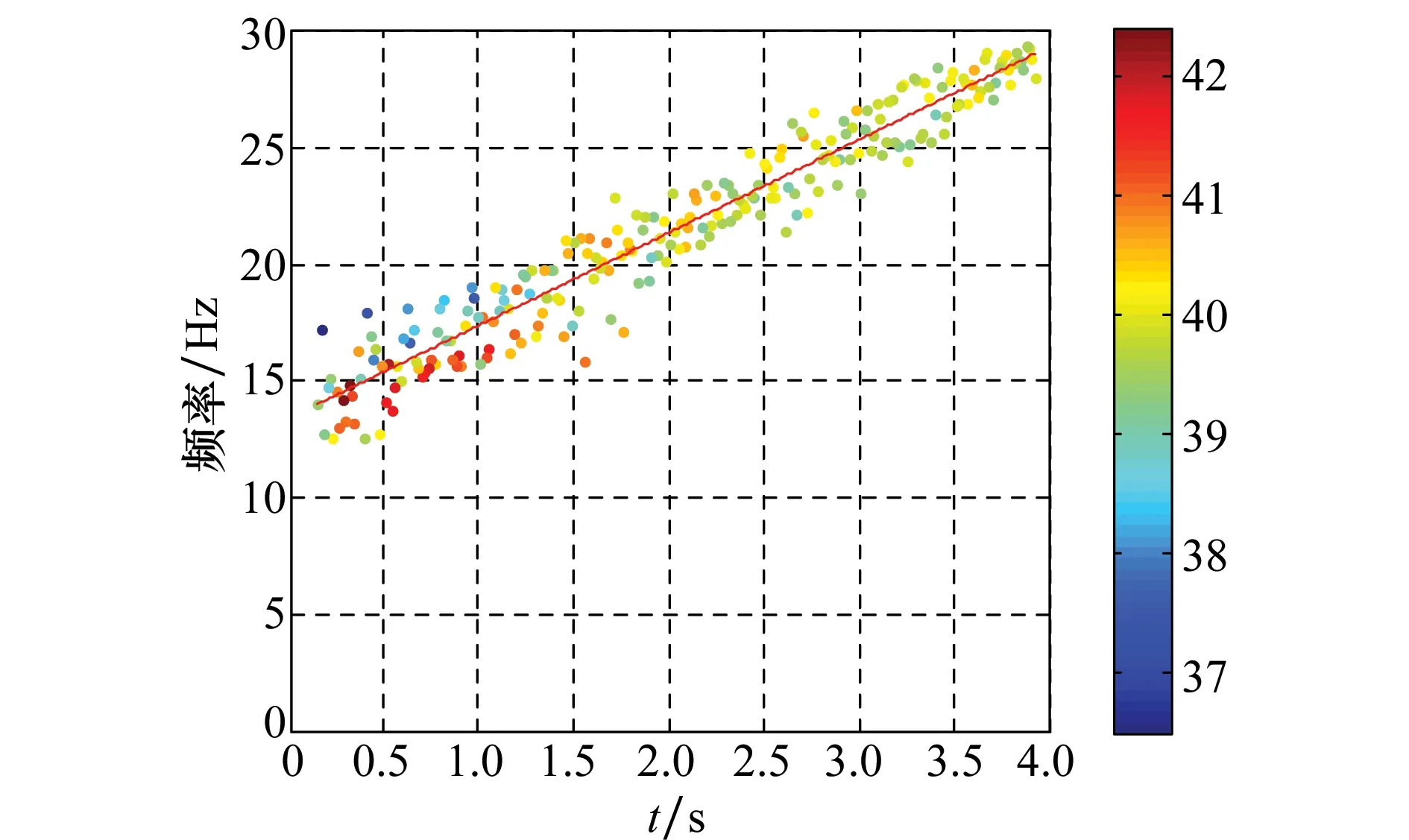
图8 目标1的HHT时频谱Fig.8 HHT spectrum of target 1

尝试Dechirp算法处理该数据,结果如图9所示。

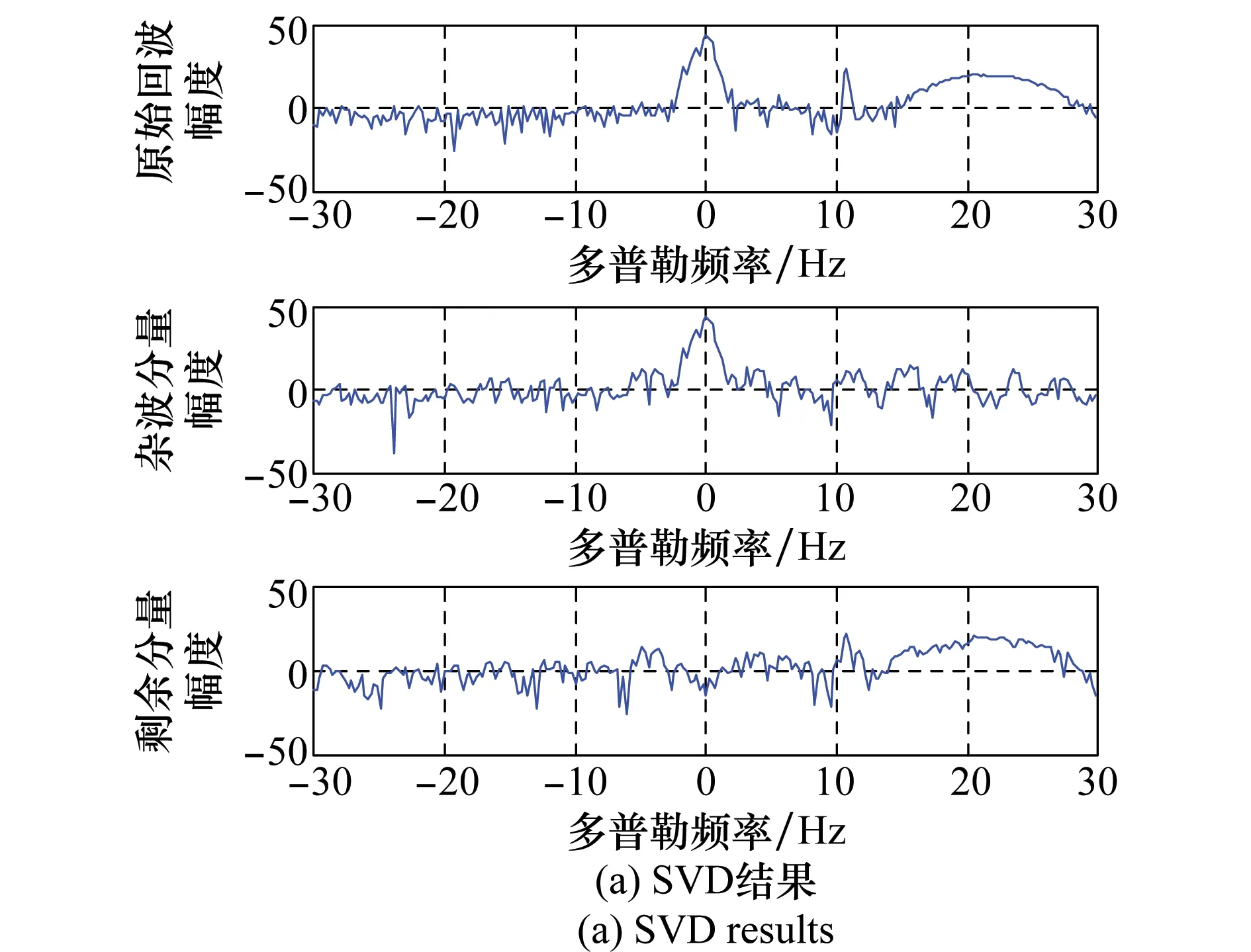
图9 多目标Dechirp计算结果Fig.9 Dechirp results under multi-objectives

由图9可知，SVD将杂波剔除后,根据信号频谱随补偿系数的变化获得目标速度和加速度的估计值,分别为100.7 m/s和29.7 m/s2。

采用与第3.1节相同的方法,分别计算HHT和Dechirp两种算法下,分析信噪比变化对目标1参数估计精度的影响(目标2信噪比始终保持为20 dB),结果如图10所示。

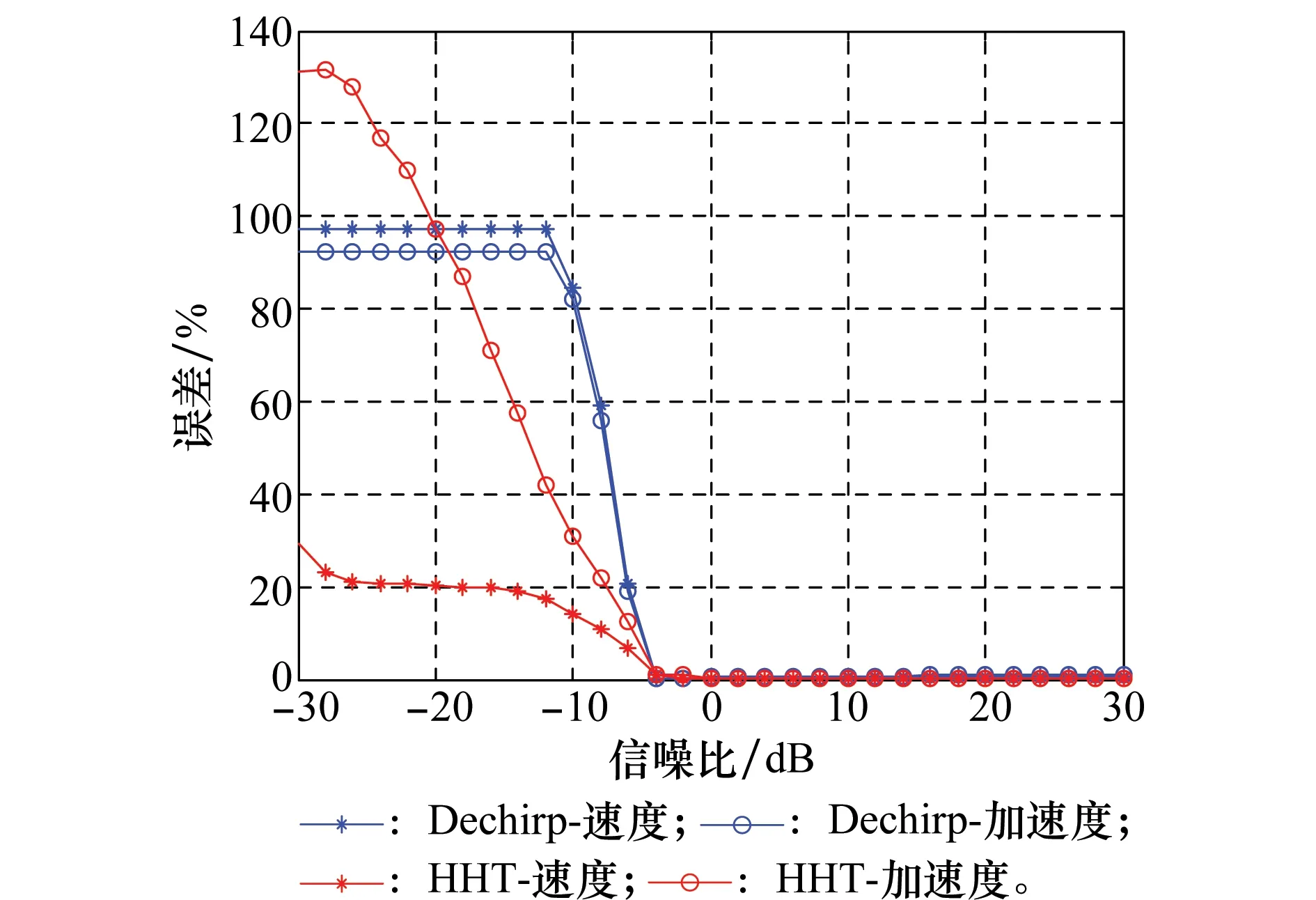
图10 不同信噪比下目标1的参数估计误差Fig.10 Estimation errors of target 1 parameters under different SNRs

由图10可知，估计误差随目标信噪比的变化趋势与单目标场景下的统计结果相似。表明算法在多目标场景下具有较强鲁棒性。

4 结 论

针对高频雷达强杂波背景下的机动目标检测问题,给出了基于HHT的机动目标参数估计算法。该算法利用CEMD从回波中分离出地海杂波和目标信号,进而计算目标不同时刻下的瞬时频率获得HHT时频图,最终通过线性拟合获得目标运动参数的估计。数据分析结果表明,该算法可以有效从强杂波背景中分离出目标信号,直接对分离出的目标信号进行参数估计,从而避免了常规算法为消除地海杂波而采取的复杂处理过程;多目标场景下的处理结果显示,该算法可以将不同目标信号分离开,进而同时对多目标进行运动参数估计,对后续检测而言可同时对多目标进行速度补偿和检测,有助于简化机动目标检测的处理流程;对不同信噪比目标的运动参数估计结果显示,随着目标信噪比的增大,速度和加速估计误差呈快速减小的趋势,信噪比大于13 dB时估计误差小于1%。

[1] 周万幸.天波超视距雷达发展综述[J].电子学报,2011,39(6):1373-1378.

ZHOU W X. An overview on development of skywave over-the-horizon radar[J].Acta Electronica Sinica,2011,39(6):1373-1378.

[2] FRAZER G J. Application of MIMO radar techniques to over-the-horizon radar[C]∥Proc.of the IEEE International Symposium on Phased Array Systems and Technology, 2016:1-3.

[3] LIU Z, SU H, HU Q. Transient interference suppression for high-frequency skywave over-the-horizon radar[J]. Iet Radar Sonar & Navigation, 2017, 10(8):1508-1515.

[4] XU J, ZHOU X, QIAN L C, et al. Hybrid integration for highly maneuvering radar target detection based on generalized radon-fourier transform[J]. IEEE Trans.on Aerospace & Electronic Systems, 2017, 52(5):2554-2561.

[5] QUAN Y, ZHANG L, LI Y, et al. OTHR spectrum reconstruction of maneuvering target with compressive sensing[J]. International Journal of Antennas & Propagation,2014,2014(10): 1-10.

[6] WANG G, XIA X G, ROOT B T, et al. Moving target detection in over-the-horizon radar using adaptive chirplet transform[J]. Radio Science, 2016, 38(4):1-24.

[7] 雷志勇, 黄银河, 周海峰, 等. 改进的通道补偿法检测高频雷达机动目标[J]. 系统工程与电子技术, 2009, 31(4): 822-825.

LEI Z Y, HUANG Y H, ZHOU H F, et al. Improved channel compensation method for maneuvering target detection in OTH radar[J]. Systems Engineering and Electronics, 2009, 31(4): 822-825.

[8] LU K, LIU X Z. Enhanced visibility of maneuvering targets for high-frequency over-the-horizon radar[J]. IEEE Trans.on Antennas and Propagation, 2005, 53(1): 404-411.

[9] XIN Z, LIAO G, YANG Z, et al. A fast ground moving target focusing method based on first-order discrete polynomial-phase transform[J]. Digital Signal Processing, 2017, 60(1):287-295.

[10] KANG B, BAE J, LEE S, et al. Isar rotational motion compensation algorithm using polynomial phase transform[J]. Microwave & Optical Technology Letters,2016,58(7):1551-1557.

[11] 胡进峰,李万阁,艾慧,等.基于改进时频分析方法的高频雷达机动目标检测算法研究[J].电子与信息学报,2015,37(8):1843-1848.

HU J F, LI W G, AI H, et al. Maneuvering target detection algorithm based on improved Ttime-frequency analysis method in skywave radar[J]. Journal of Electronics & Information Technology, 2015, 37(8): 1843-1848.

[12] XIA X G. Discrete chirp-Fourier transform and its application to chirp rate estimation[J].IEEE Signal Process，2008,48(11): 3122-3133.

[13] SURESH P, THAYAPARAN T, VENKATARAMANIAH K. Fourier-Bessel transform and time-frequency-based approach for detecting manoeuvring air target in sea-clutter[J]. Iet Radar Sonar & Navigation, 2015, 9(5):481-491.

[14] 李雪, 郭晓彤, 王岳松,等. 基于已知传播模式数目的海杂波抑制方法研究[J]. 电波科学学报, 2016, 31(4):700-705.

LI X, GUO X T, WANG Y S, et al. Sea clutter suppression algorithm based on ionospheric propagation mode number[J]. Chinese Journal of Radio Science, 2016, 31(4):700-705.

[15] CHEN Z, HE C, ZHAO C, et al. Using SVD-FRFT filtering to suppress first-order sea clutter in HFSWR[J]. IEEE Geoscience & Remote Sensing Letters, 2017, PP(99):1-5.

[16] 薄超, 顾红, 苏卫民. 基于高阶奇异值分解的 OTHR 海杂波抑制算法[J]. 系统工程与电子技术, 2014, 36(5):872-878.

BO C, GU H, SU W M. OTHR sea clutter suppression algorithm based on higher order singular value decomposition[J]. Systems Engineering and Electronics, 2014, 36(5):872-878.

[17] HUANG N E, SHEN Z, LONG S R, et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A, 1998, 454(1971): 903-995.

[18] TANAKA T, MANDIC D P. Complex empirical mode decomposition[J]. IEEE Signal Processing Letters, 2007, 14(2): 101-104.

[19] ALTAF M U, GAUTAMA T, TANAKA T, et al. Rotation invariant empirical mode decomposition[C]∥Proc.of the IEEE International Conference Acoustics, Speech, Signal Processing, 2007, 3: 1009-1012.

[20] GÜNTÜRKÜN U. Bivariate empirical mode decomposition for cognitive radar scene analysis[J]. IEEE Signal Processing Letters, 2015, 22(5):603-607.

[21] 杜陈艳,张榆锋,杨平,等. 经验模态分解边缘效应抑制方法综述[J]. 仪器仪表学报, 2009, 30 (1): 55-60.

DU C Y, ZHANG Y F, YANG P, et al. Ap-proaches for the end effect restraint of empirical mode decom-position algorithm[J].Chinese Journal of Scientific Instrument,2009,30(1): 55-60.

[22] ZHAO J, ZHAO P, CHEN Y. Using an improved BEMD method to analyse the characteristic scale of aeromagnetic data in the gejiu region of Yunnan, China[J]. Computers & Geosciences, 2016, 88(7):132-141.

[23] ZHENG J, CHENG J, YANG Y. Partly ensemble empirical mode decomposition: an improved noise-assisted method for eliminating mode mixing[J].Signal Processing,2014,96(3):362-374.