基于不完备信息的粗糙集初始备件品种确定方法
董骁雄, 陈云翔, 蔡忠义, 孟祥飞
(空军工程大学装备管理与安全工程学院,陕西 西安 710051)
0 引 言
确定初始备件品种是制定装备初始备件清单的主要任务之一,其合理与否直接影响装备部署初期的可用度。若初始备件品种不足会导致装备故障后不能进行更换修理,从而降低装备使用可用度;若初始备件品种过剩,则会增加大批不必要备件的管理工作,加重保障压力与寿命周期费用。目前国内外对备件的研究大多集中在备件需求确定和库存配置方面[1-4],而确定备件品种是确定备件需求和库存配置的必要前提,只有科学地确定备件品种,才能保证备件需求和库存的合理性,所以备件品种确定方法具有重要研究价值。
传统的备件品种确定方法包括逻辑决断法、价值系数法、模糊理论和灰色理论等[5-8]。上述方法主要有以下不足:①主观性较强,受评价人员自身影响较大;②以价值系数作为备件设置的评判标准可能导致部分价格高的专用件,因其价值系数较低,就没有进行设置;③上述方法均适用于备件属性信息全部明确的情形,对备件属性信息不完备的情形难以解决。针对备件信息不完备的情况,文献[9]提出基于不完备信息的粗糙集备件品种确定方法,文献[10]提出飞机初始备件品种优化的集对-粗糙集方法,但上述方法使用经典粗糙集的相容关系,认为备件品种属性值未知时和任意属性值均相等,会造成实际无相同属性值的备件品种被归为一类,导致决策不准确;其次,上述方法均未考虑备件品种的属性权重,在备件品种的决策过程中,属性的重要度往往不同,不考虑属性权重是不符合实际情况的。
针对上述情况,首先系统分析影响初始备件品种的主要因素;然后针对初始备件信息不完备的特点,构建基于加权阈值相容关系的不完备信息系统粗糙集模型,提出基于系统信息量的属性权重确定方法,避免主观因素的影响。为解决初始备件品种确定问题,提供了可靠有效的方法。
1 初始备件品种影响因素分析
初始备件品种决策受多方面因素影响,应进行综合考虑[11],包括装备的研制方案、使用保障方案和寿命周期费用等。备件品种确定影响因素如图1所示。
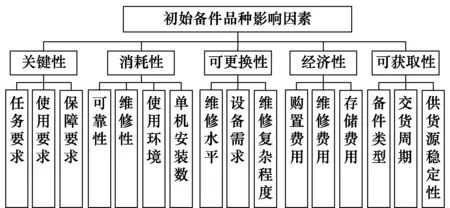
图1 初始备件品种决策影响因素集Fig.1 Factors that affect the determinants of the initial spare parts
(1) 关键性
关键性表现为备件品种在装备中发挥的作用和对装备性能的影响程度,装备完好率、任务成功率指标要求越高,该备件品种越关键,越有必要储备。关键性因素的一项指标是严酷度类别,它是故障模式所产生后果严重程度的度量表示,可通过故障模式影响分析获取。严酷度等级越严重,越应该考虑备件的配置。
(2) 消耗性
消耗性主要指在装备保障期间,备件失效可能性的大小或消耗的多少。分为正常消耗和故障消耗,正常消耗件通常指一次使用备件,出现故障或用到规定使用寿命后即应报废而不可修复的备件;故障消耗件通常指多次使用备件,出现故障后能够修复或用到规定使用寿命后经检修可以再次使用的备件。实际中,备件消耗性需要综合考虑装备的可靠性、使用环境、单机安装数、修理能力等因素。一般备件消耗越大,越有必要储备。
(3) 可更换性
可更换性主要指备件在相应修理级别能够拆装更换的特性,由外场可更换单元(line replaceable unit, LRU)、内场可更换单元(shop replaceable unit, SRU)和修理级别决定。备件消耗性还需要综合考虑修理能力和维修复杂程度等因素。
(4) 经济性
经济性主要指备件的成本,包括备件的采购费、修理费以及库存费等。价值越高的备件,采购价格和库存费用都较高,越应谨慎考虑是否储备该品种。在战时还需要考虑军事意义,对于关键备件,即便十分贵重,也要适量存储。一般备件品种的价值越高,越要谨慎考虑是否储备。
(5) 可获取性
可获取性指产生备件需求时,获得备件的时效性。主要有3个影响因素:①备件是否为标准件;②备件的交货周期;③货源是否为进口。如初始备件中的标准件市面上容易采购,获取周期较短;而如发动机叶片等贵重件、非标准件供应商一般无存货,需要提前订购,采购周期较长;如果是进口件,受国际形势影响可能采购周期很长,应在装备保障预案中予以重点考虑。
2 不完备信息系统
在初始备件品种多属性决策中,由于装备处于初始部署阶段,其运行状态、故障规律、维修难度等状况难以掌握,属性通常未知,所以初始备件品种决策是不完备的信息系统,该系统相关定义如下。
定义1[12]S=(U,A,V,f),U为对象的非空有限集合;A=C∪D为属性的非空有限集合,C为条件属性的非空有限集,D为决策属性的非空有限集合;V是A的属性值集合,Va是属性a∈A的值域;Va可以为实数值的连续型数据,也可以为语言描述型数据。f是信息函数,f:U×A→V,即f(x,a)∈Vaf,表示指定U中每一个对象x的属性值。若S中至少有一个属性a∈A,使Va含有空值(*),则称S是不完备信息系统。
定义2[13](上、下近似)Pawlak近似空间AS=(U,A),∀X⊆U,∀R∈A,X的R下近似集R-X和R上近似集R+X分别为U上的普通集合,则
R-X={x∈U|[x]R⊆X}
R+X={x∈U|[x]R∩X≠Ø}
(1)
posR(X)=R-X称为X的R正域,negR(X)=U-R+X称为X的R负域,bnR(X)=R+X-R-X称为X的R边界域。上、下近似粗糙集理论刻画不确定性的基础。由上述定义可知,X的R下近似是包含在X中的最大可定义集;X的R上近似是包含X的最小可定义集。
定义3假设决策属性d把U分成有限的类,C1={C1t,t∈T},T={1,2,…,l},则对象中的任意x∈U只属于一个C1t∈C1,假设该分类有序,即对于全部r,s∈T,若r>s,则C1r优于C1s中的对象,为了处理多属性的偏好信息,定义决策类C1t的向上累积集和向下累积集[14]为
(2)
3 粗糙集方法
传统粗糙集方法运用经典相容关系对问题的论域分类得到粗糙近似,获取决策规则。本文改进经典相容关系决策条件过于宽松的不足,提出加权阈值相容关系代替经典相容关系进而获取决策规则,作为初始备件品种不完备信息粗糙集方法的核心。
3.1 经典相容关系
定义4给定信息系统S=(U,A,V,f),kryszkiewic[15]给出“相容关系”定义∀φ⊂P⊆A确定了U上的一个二元关系TP,即
TP(x,y)⟺∀a∈P,f(x,a)=f(y,a)∨
f(x,a)=*∨f(y,a)=*x,y∈U
(3)
由定义可知,相容关系认为未知值和任意属性值均相同,可能造成实际无相同属性值的对象被误归为同类,条件过于宽松。
3.2 联系度相容关系
定义5给定信息系统S=(U,A,V,f),在定义4的基础上引入阈值α1与α2(0≤α1≤α2≤1)。将非“*”的属性数目在B中所占比例小于α1的对象剔除,由剩余对象构成新论域U′,将取值相同属性比例不小于α2且无不同属性值的两个对象归为一类[16]。
(x)={y∈U′|u(x,y)=
a+bi,a+b=1,α≥α2}
(4)
式中,a、b分别为x、y在属性子集B上属性取值相同、不同的比例。
定义5结合阈值及决策者的主观要求对归类的严格程度进行改进,且保持了自反性和对称性,但将非“*”的属性数目在B中所占比例小于α1的对象剔除,会造成联系度相容类不完整。
3.3 τ限制相容关系
定义6引入阈值τ(0≤τ≤1),τ限制相容关系定义[17]为
ILR(B,τ)={(x,y)|∈U×U|∀b∈B(b(x)=b(y))
∨(PB(x)∩PB(y)≥|A|×τ)∧∀b∈B(b(x)≠*)
∧(b(y)≠*)→(b(x)=b(y)}
(5)
τ限制相容关系ILR(B,τ)包括两类情况:①B中全部属性值均对应相同(取值相等或都是“*”);②B中取值相同属性比例不小于τ且没有不同属性值。
由定义可知,τ限制相容关系第一类情况可能使所有属性值为“*”,而实际无相同属性值的对象归为同类,条件依然宽松。
吸取上述粗糙集模型的优点、改进不足,提出加权阈值相容关系,更符合实际情况,具有更强的适应能力。
3.4 加权阈值相容关系
定义7给定信息系统S=(U,A,V,f)。B⊆A,0≤w(b)≤1为属性b在B中的权重,加权阈值相容关系定义为
(6)
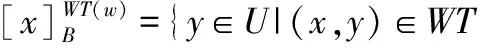
由式(6)可知,对象x与y仅在属性子集B中取值相同的属性权重和大于w且无不同属性值时,会被归为一类。避免了没有相同属性值的对象被归为一类的现象。
阈值w起到了约束条件的作用,w越大,加权阈值相容关系要求两个对象之间共同的非空属性越多,这时对象归入某优势类的确定性越大,误分类的概率越小,对不完备信息系统的分类更符合实际,得到的决策规则可信度也越高。同时,阈值w是决策者依据实际情形设定的,这使得决策分析方法具备一定的灵活性和适应性。
定义8给定信息系统S=(U,A,V,f),B:B⊆A,对象集X关于属性子集B的加权阈值相容关系的上近似BWT(w)(X)和下近似BWT(w)(X)[18]分别为
(7)
3.5 提取决策规则
依据式(7)获得确定性决策规则[19]为
iff(x,q1)≥rq1,f(x,q2)≥rq2,…,f(x,qp)≥rqp
其中
(8)
根据定义7中的上下近似,可以得到确定性决策规则,即
iff(x,q1)≤rq1,f(x,q2)≤rq2,…,f(x,qp)≤rqp
其中
(9)
4 基于系统信息量的属性权重确定
定义9给定信息系统S=(U,A,V,f),U={x1,x2,…,x|U|},B⊆C的信息量定义[20]为
(10)
其中,|X|表示集合X的基数。
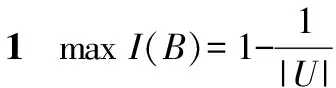
由性质1知,若通过属性集B可以划分U中的每个对象,则B所提供的信息量最大;若B无法划分U中任意两个对象,则B所提供的信息量为零。
定义10给定信息系统S=(U,A,V,f),定义属性b∈B⊆C在属性集B中的重要度为
SigB{b}(b)=I(B)-I(B{b})
(11)
由定义2可知,属性集B中的属性b在B中的重要性由去掉该属性引起的信息量变化程度进行度量。特别地,单个属性的重要性Sigφ(b)=Sig(b)=I({b}),b在B中的权重通过重要度归一化后确定,即
(12)
5 算例分析
设某新型装备的初始备件品种决策表如表1所示。U={u1,u2,u3,u4,u5,u6,u7,u8,u9,u10}。根据第1节,初始备件品种决策有5个条件属性b={b1,b2,b3,b4,b5}和1个决策属性d。各属性值为b1={关键,重要,一般}={2,1,0},b2={消耗,易损,不损}={2,1,0},b3={可更换,不可更换}={1,0},b4={订货周期大于3个月,订货周期1~3个月,订货周期1个月以内}={2,1,0},b5={昂贵,一般,低廉}={2,1,0};决策属性d={不设置,设置}={1,0},未知属性记为“*”。
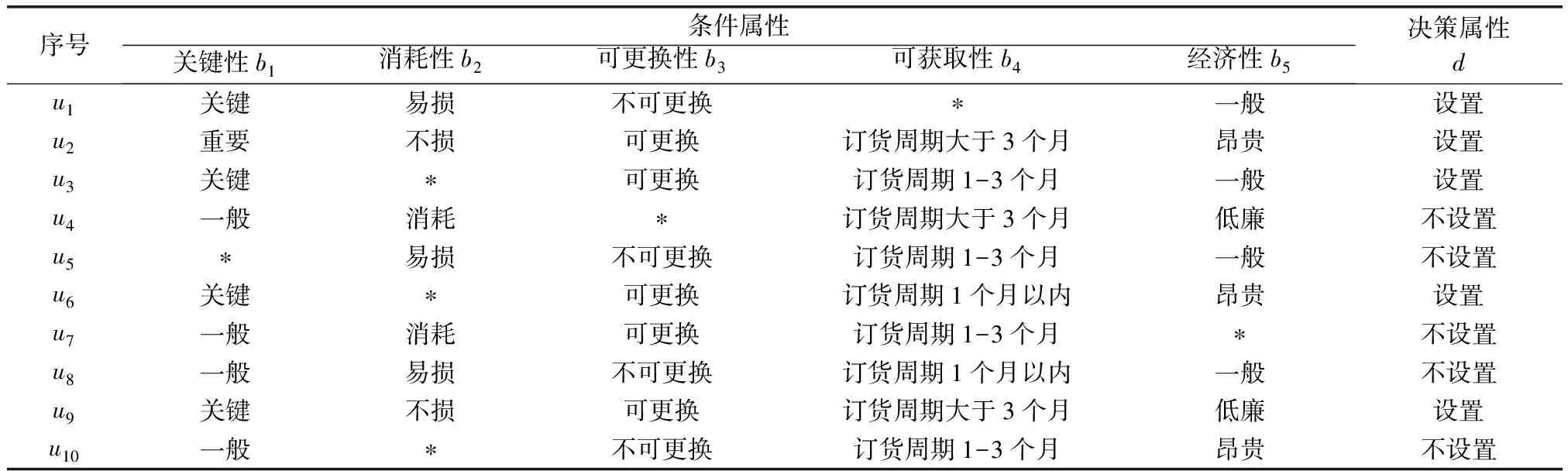
表1 某新型装备初始备件品种决策表
由表1可知,初始备件品种属性的空值较多,这是由于新型装备的工作状态、故障规律、维修难度等情况不易掌握所致,符合实际情况。根据式(10)~式(12)求得属性权重为
I(B)=0.88
SigB(b1)=I(B)-I(B{b1})=0.04
SigB(b2)=I(B)-I(B{b2})=0.02
SigB(b3)=I(B)-I(B{b3})=0.03
SigB(b4)=I(B)-I(B{b4})=0.04
w(b1)=0.27,w(b2)=0.13,w(b3)=0.2,
w(b4)=0.27,w(b5)=0.13
在加权阈值相容关系下,取阈值ω=0.4时,根据式(6)得到
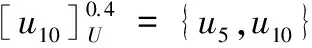
决策属性d将U划分为设置对象集合M={u1,u2,u3,u6,u9}和不设置对象集合N={u4,u5,u7,u8,u10},根据式(7)得到
BWT(w)(M)={u2,u6,u9}
BWT(w)(M)={u1,u2,u3,u5,u6,u7,u8,u9}
BWT(w)(N)={u4,u10}
BWT(w)(N)={u1,u3,u4,u5,u7,u8,u10}
根据式(8)和式(9)得到确定性决策规则如表2所示。

表2 偏好决策规则集
由表2可知:
(1) 若备件品种的关键性至少为重要,可更换,且订货周期大于3个月,则设置该备件品种。
(2) 若备件品种关键,可更换且昂贵,则设置该备件品种。
(3) 若备件品种的关键性一般且价格昂贵,则不设置该备件品种。
(4) 若备件品种的关键性一般,可更换且不耗损,则不设置该备件品种。
由上述分析过程可知,相对于文献[9-10]使用经典粗糙集的相容关系,使实际没有相同属性值的备件品种被归为一类,导致决策不准确;本文采用加权阈值相容关系,更符合实际情况,具有更强的适应能力。相对于文献[9-10,21]没有考虑备件品种的属性权重,本文提出基于系统信息量的属性权重确定方法,无需引入系统外知识,权重确定更科学客观,提高了初始备件品种决策精度。
6 结 论
针对初始备件品种确定问题,提出基于不完备信息的粗糙集初始备件品种确定方法,该方法能够科学合理地确定初始备件品种,为装备制定初始备件清单提供决策依据,保证备件需求和库存配置的准确性。为进一步提高方法的适用性,需要针对以下问题作更深入的研究:①需要进一步量化备件品种的条件属性,提高决策的准确性;②加权阈值粗糙集关系下,需要进一步研究科学确定阈值取值的方法,确定阈值的最优取值。
[1] HU Q, CHAKHAR S, SIRAJ S, et al. Spare parts classification in industrial manufacturing using the dominance-based rough set approach[J].European Journal of Operational Research,2017,262(3):1136-1163.
[2] GUO F, GIAO J, ZHAO Q H, et al. A double-level combination approach for demand forecasting of repairable airplane spare parts based on turnover data[J]. Computers and Industrial Engineering, 2017, 110(8): 92-108.
[3] ROSIENKIEWICZ M, CHLEBUS E, DETYNA J. A hybrid spares demand forecasting method dedicated to mining industry[J]. Applied Mathematical Modelling, 2017, 49(9): 87-107.
[4] ZHU Q, LIU S Y, HUANG Z J, et al. Prediction model of spare parts consumption based on engineering analysis method[J]. Procedia Engineering, 2017, 174(3): 711-716.
[5] REN X, ZHAO J J, LI B. Spare parts varieties level configuration based on grey situation decision[C]∥Proc.of the 26th Chinese Control and Decision Conference, 2014: 2241-2243.
[6] JIANG M, MA S S, YANG S Y. Research on the confirm method for new system radar spare parts based on gray AHP[C]∥Proc.of the Modern Engineering Solutions for the Industry, 2015:735-744.
[7] ZHANG Z, KANG R, QU L, et al. Method of determining spares varieties based on AHP and DEA[C]∥Proc.of the 8th International Conference on Reliability, Maintainability and Safety, 2009: 590-593.
[8] 崔国伟,王正,张登滨.场站转场条件下备件携行品种研究[J].航空装备与技术, 2016,12(1): 113-116.
CUI G W, WANG Z, ZHANG D B. Spare parts variety determination for liquid rocket engine with zero-failure data[J]. Aviation Equipment and Technology,2016,12(1): 113-116.
[9] 黄建新, 杨建军, 张志峰. 基于不完备信息的粗糙集确定备件品种[J]. 装备指挥技术学院学报, 2005, 16(3): 45-47.
HUANG J X, YANG J J, ZHANG Z F. Defining the class of spare parts based on the rough set of incomplete information[J]. Journal of the Academy of Equipment Command and Technology, 2005, 16(3): 45-47.
[10] 车飞,陈云翔.飞机初始备件品种优化的集对一粗糙集方法[J]. 数学的实践与认识,2011, 41(9): 202-206.
CHE F,CHEN Y X.Optimized method of aircraft initial spares variety based on set pair analysis and rough set[J]. Mathematics in Practice and Theory, 2011, 41(9): 202-206.
[11] MUCKSTADT J A. Analysis and algorithms for service parts supply chains[M]. Beijing: National Defense Industry Press, 2016: 31-42.
[12] LIANG J Y, XU Z B. The algorithm on knowledge reduction in incomplete information systems[J]. International Journal of Uncertainty, Fuzziness and Knowledge-based Systems, 2002, 10(1): 95-103.
[13] STEFAMOW J, TSOUKEAS A. On the extension of rough sets under incomplete information[J]. International Journal of Intelligent System, 1999, 16(1): 29-38.
[14] GRECO S, MATARAZZO B, SLOWINSKI R. Rough sets theory for multicriteria decision analysis[J]. European Journal of Operational Research, 2001, 129(1): 1-47.
[15] KRYSCKIEWICZ M. Rough set approach to incomplete information system[J]. Information Sciences, 1998, 112(1): 39-49.
[16] PAWLAK Z, BUSE J G, SLOWINSKI R. Rough sets[J]. Communications of the ACM, 1995, 38(11): 89-135.
[17] STEFANOWSKI J. Incomplete information tables and rough classification[J]. Computational Intelligence, 2001, 17(3): 546-564.
[18] FANG B W, HU B Q. Probabilistic graded rough set and double relative quantitative decision-theoretic rough set[J]. International Journal of Approximate Reasoning,2016,74:1-12.
[19] GRECO S, INUIGUCHI M, SLOWINSKI R. Fuzzy rough sets and multiple-premise gradual decision rules[J]. International Journal of Approximate Reasoning, 2006, 41(2): 179-211.
[20] GUAN J W, BELL D A, GUAN Z. Matrix computation for information systems[J]. Information Sciences, 2001, 131(1): 129-156.
[21] 池阔, 康建设,王广彦,等.基于完备相容Rough决策表的备件品种确定方法[J].火力与指挥控制,2015,40(10): 107-110.
CHI K, KANG J S, WANG G Y, et al. Method for varieties of spare parts based on complete compatible rough decision table[J]. Fire Control and Command Control, 2015, 40(10): 107-110.

