基于相位的岸基雷达地海杂波分割方法

夏晓云, 黎 鑫,2, 张玉石, 万晋通

(1. 中国电波传播研究所，电波环境特性及模化技术重点实验室, 山东 青岛 266107; 2. 西安电子科技大学雷达信号处理国家重点实验室, 陕西 西安 710071)

0 引 言

海杂波作为不可避免的雷达回波,常常严重制约雷达对舰船、飞机、导弹等目标的探测能力[1]。相关研究表明[2-3],海杂波不仅受雷达参数的影响,如雷达频率、极化、擦地角、带宽等,还受气候、环境等不确定自然因素的影响,如风速、风向、地理环境等,导致了海杂波的复杂多变特性。为了分析海杂波的特性,需要采集和积累完备的海杂波数据。国内外已经开展了大量海杂波测量实验和海杂波特性研究工作[4],如著名的加拿大McMaster大学的X波段IPIX雷达海杂波测量实验[5]、澳大利亚国防科技署(DSTO)的海杂波测量实验[6-9]等。利用岸基雷达对海面进行长期观测和数据采集是一种积累不同测量条件下海杂波数据的有效手段。目前岸基预警雷达仍然是我国近海监视力量的主体[10],因此,岸基雷达杂波数据的有效处理也成为杂波特性认知、岸基雷达目标探测性能提升的必要条件。

然而,对于岸基对海观测雷达来说,一方面,由于雷达旁瓣和后瓣的存在,海杂波数据的采集受雷达架设位置及周围地理环境的影响较大,另一方面,由于近海岸线复杂地理特征及海水涨退潮等自然现象的存在,雷达测得的近岸杂波数据相比开放海域的杂波数据要复杂得多[11]。对近岸海域杂波特性的研究[12-14]表明了近岸杂波的复杂性。文献[15-16]指出近海岸是由不同种类的杂波组成的复杂环境,这对杂波特性的认知及对海雷达的检测性能有很大影响。

在遥感图像处理中海岸线位置提取是重要的一步,对海上目标的提取和识别有重要作用[17]。而对于岸基雷达来说,如何通过杂波数据的分析来提取海岸线信息,对杂波特性分析具有重要意义。本文通过对岸基S波段雷达回波数据分析,提出基于相位的岸基雷达地海杂波分割方法。由于岸基雷达与地物杂波呈相对静止状态,地物杂波的多普勒偏移为零,海面具有相对于雷达的运动,因此海杂波具有非零的多普勒偏移和明显的多普勒展宽,这些差异在相参雷达回波的相位上有明显的不同。本文利用回波的相位信息可以快速有效地区分具有不同频移特性的地物杂波和海杂波。对近岸不同距离门杂波的幅度分布特性的分析结果也从侧面表明了该分割方法的有效性,为岸基雷达杂波数据的处理提供了方法依据。

1 实测数据分析

本文分析数据为某岸基S波段全相参脉冲体制雷达测得的杂波数据。雷达架设在海拔大于400 m的山顶上,工作方式为扫描模式,距离分辨率为60 m。雷达工作环境示意图如图1所示,图中曲线DABC为根据地图刻画的海岸线位置,其中ABC为雷达中心波束照射范围,D点位置为雷达中心波束照射范围外距雷达最远的岛礁。

图1 雷达工作环境示意图Fig.1 Radar working environment sketch map

雷达工作中,在中心波束指向由OA位置扫描到达OC位置的过程中进行数据采集,一个扫描周期结束后,雷达中心波束指向重置到OA位置,再次开始从OA位置到OC位置的数据采集,如此重复获得多个扫描周期的数据。由于受雷达工作平台的限制,雷达回波中存在地物杂波。由图1可知,地杂波不仅存在于雷达主瓣的照射范围,还存在于雷达旁瓣中,且旁瓣地杂波存在的距离不同于主瓣。因此在进行海杂波特性分析之前,必须对雷达回波中的地物杂波和海杂波进行有效划分。实验中已知雷达正视方向的临海处有一座小山,雷达波束照射到该位置时会产生很强的回波,在杂波幅度(所有波位回波幅度的平均值)随距离门变化的曲线中会出现明显的尖峰,如图2所示。

图2 雷达回波幅度值随距离门的变化Fig.2 Variation of radar echo amplitude with range cells

由图2可知，尖峰位置出现在第27个距离门,从第30个距离门开始幅度值趋于缓变状态,因此,在实际杂波数据处理过程中,通常以此为依据对地物杂波和海杂波进行简单划分,即粗略地将第30个距离门开始的回波数据用作海杂波特性的分析。由图1可知,雷达正视方向为地形的凹口位置,雷达整个观测范围的海岸线与雷达距离的动态范围较大,因此根据典型地形特征得到的地海杂波分割结果往往存在较大偏差。可以通过对雷达回波数据的具体分析说明这一问题。

1.1 幅度强度分析

雷达回波幅度值的大小代表了散射体散射特性的强弱,同时也反映了不同散射体之间的特性差异。一组海杂波数据的幅度图如图3所示,每个扫描周期194个波位,图中显示为3个扫描周期的数据,距离门范围为30～129,图中显示颜色越亮表示回波幅度值越大。

图3 雷达回波幅度图Fig.3 Map of radar echo amplitude

由图3可知,距离门30～50左右的回波幅度值明显偏大,这些回波幅度值较大的强回波信号跨越多个距离门多个波位且在每个扫描周期具有相似的结构,说明这些引起强回波信号的散射点不是随机出现而是固定存在的。在每个扫描周期中,强散射点的回波幅度值在不同波位之间存在较大变化且不具有规律性,由此可以排除雷达本身对回波数据带来的影响。进一步对比图1与图3发现,图3中回波幅度值较大的区域轮廓与图1中海岸线轮廓形状上是相似的,且由于地物杂波相比海杂波的强度要大得多,因此推测这些强回波是地物杂波,是由雷达观测区域的地理环境引起的。

1.2 多普勒谱分析

海表面存在各种各样的特征,如浪谷、浪楔、波浪、泡沫、漩涡、浪花以及海浪下落时形成的大大小小的水花等,这些变化的特征使得海表面相对雷达来说是一个动态的、不断变化的粗糙面[1]。海表面各种各样的特征不同运动状态导致海杂波多普勒谱存在频移与展宽。而对于地面、浅滩、礁石等特征来说,其与岸基雷达呈相对静止状态,因此地物杂波多普勒谱表现为在零频处有一个很窄的尖峰。基于地物杂波与海杂波多普勒谱特性的差异,对图3所示雷达回波数据的多普勒谱作进一步分析。

雷达工作在扫描模式,每个波位发射100个连续的相参脉冲,因此文中利用每个雷达分辨单元对应的100个相参脉冲回波数据进行谱估计。雷达回波多普勒谱如图4所示。

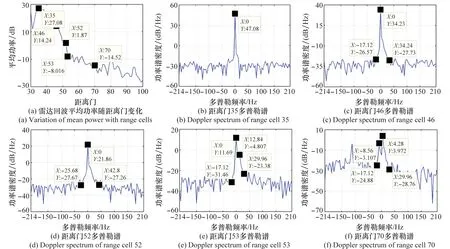
图4 雷达回波多普勒谱Fig.4 Doppler spectrum of radar returns

由图4(a)可知第33个波位雷达回波平均功率随距离门的变化,前52个距离门的回波功率明显高于其他距离门的回波功率。计算第33个波位每个距离门的多普勒功率谱进行观察,选择具有代表性的距离门35(强回波单元处)、46、52(强回波单元回波功率下降过程中)、53(强弱回波单元交界处)和距离门70(弱回波单元处)进行多普勒谱显示分析。由图4(b)可知距离门35杂波单元的多普勒功率谱,杂波谱为较窄的单峰且多普勒中心频率为0 Hz,与地杂波谱特性吻合。由图4(c)和图4(d)分别可知距离门46和52杂波单元的多普勒功率谱,杂波谱仍为单峰且多普勒中心频率为0 Hz,但谱峰两侧出现谱展宽,展宽是由海杂波引起的,说明地、海杂波混合在一起,但由于地物杂波比海杂波强得多,因此该杂波单元中地物杂波是占优的。由图4(e)可知距离门53杂波单元的多普勒功率谱,杂波谱多普勒中心频率仍为0 Hz,但在12.84 Hz处出现小的谱峰,有明显的频谱展宽,表现出了海杂波的谱特性。由图4(f)可知距离门70杂波单元的多普勒功率谱,杂波谱多普勒中心频率为4.28 Hz,另一个谱峰的频移为-8.56 Hz,杂波谱出现明显的双峰和频谱展宽现象,与海杂波谱特性吻合。实验结果展现了近海岸杂波多普勒谱特性随距离门的变化过程,表明了前52个距离门杂波单元中地物杂波的存在,验证了近岸的强回波信号是由地物杂波引起的这一推测。进一步对第96个波位、第138个波位回波数据的多普勒谱进行相同分析,得出的结论是一致的。

2 基于相位的地海杂波分割方法

在第1节中通过对雷达回波数据的分析,认为近岸回波数据中的强回波信号是由地物杂波引起的。由于地物杂波与海杂波特性存在较大差异,因此在近岸杂波数据处理过程中首先对地海杂波进行分割处理是非常必要的。本文从岸基雷达地海杂波的多普勒特性差异着手,基于雷达回波数据进行地海杂波分割处理。

频率f、角频率w与相位θ的关系可以表示为

(1)

对于岸基雷达,地物杂波的多普勒频率为零,也就是说其回波相位的变化量为零。假设某一雷达分辨单元的N相参脉冲回波为z1,z2,…,zN,均为复数。复数可以表示为模值和辐角的形式,在0～2π之间的辐角称为辐角主值,而对于雷达回波数据zn(n=1,2,…,N)来说,其模值代表回波的幅度,辐角主值则代表回波解缠绕后的相位。相参脉冲串与散射体的相互作用形成回波脉冲串,对于岸基雷达来说,静止散射体回波脉冲串中每个脉冲解缠绕后的相位是相同的,即回波复数的辐角主值是相等的。在复平面上,复数可以用向量来表示,因此两复数的辐角主值相等可以表示为两向量的夹角为0°,基于此可以利用相位信息来判断回波散射体相对雷达的运动状态,具体实现为

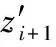
(2)

(3)

(4)

式(2)中，(·)′表示复数取共轭。式(3)中,Δi表示某雷达分辨单元中第i个脉冲与第i+1脉冲回波的相位变化量;abs(·)表示取绝对值;arctan(·)表示反正切函数;imag(·)表示取复数的虚部;real(·)表示取复数的实部。式(4)中,ε表示某雷达分辨单元中相邻脉冲间相位的平均变化量;简称为相位平均变化量,δ表示判决门限。

根据式(2)和式(3),对实测数据第20～29距离门的地杂波单元和第71～80距离门的海杂波单元相邻脉冲间的相位变化量进行计算,其中地杂波单元相邻脉冲间相位变化量的均值为0.033,海杂波单元相邻脉冲间相位变化量的均值为0.505,这表明通过相位平均变化量ε的大小可以明显区分地海杂波。根据实测数据的分析结果取δ=0.04作为门限值,若ε小于给定的门限表示该雷达分辨单元的散射体相对雷达是静止的,否则反之。判断为静止状态的雷达分辨单元用1表示,代表地物杂波或地物杂波占优的单元;判断为运动状态的雷达分辨单元用0表示,代表海杂波或海杂波占优的单元。

对分割处理得到的0/1矩阵进行八邻域中值滤波处理,以滤除孤立点。对于0/1结果矩阵中的任意元素A(x,y),对其进行八邻域中值滤波处理,可以表示为

A′(x,y)=median{A(x-1,y-1),A(x-1,y),

A(x-1,y+1),A(x,y-1),A(x,y+1),

A(x+1,y-1),A(x+1,y),A(x+1,y+1)}

(5)

八邻域中值滤波处理后得到最终的地海杂波分割结果,如图5所示。

图5 地海杂波分割结果图 Fig.5 Result of sea-land clutter segmentation

由图5地海杂波分割结果可知,分割为地杂波的单元为第30～52个距离门,因此进一步分析第30～52个距离门杂波幅度分布特性与第53～60个距离门杂波幅度分布特性的差异。

分别利用瑞利分布、威布尔分布和K分布模型进行幅度分布拟合,采用卡方拟合优度检验,每个距离门的幅度分布拟合结果均为K分布拟合效果更好,但不同距离门间的分布参数存在差异,每个距离门估计的K分布参数如表1所示,表中只显示了距离门30～51中部分距离门的参数。

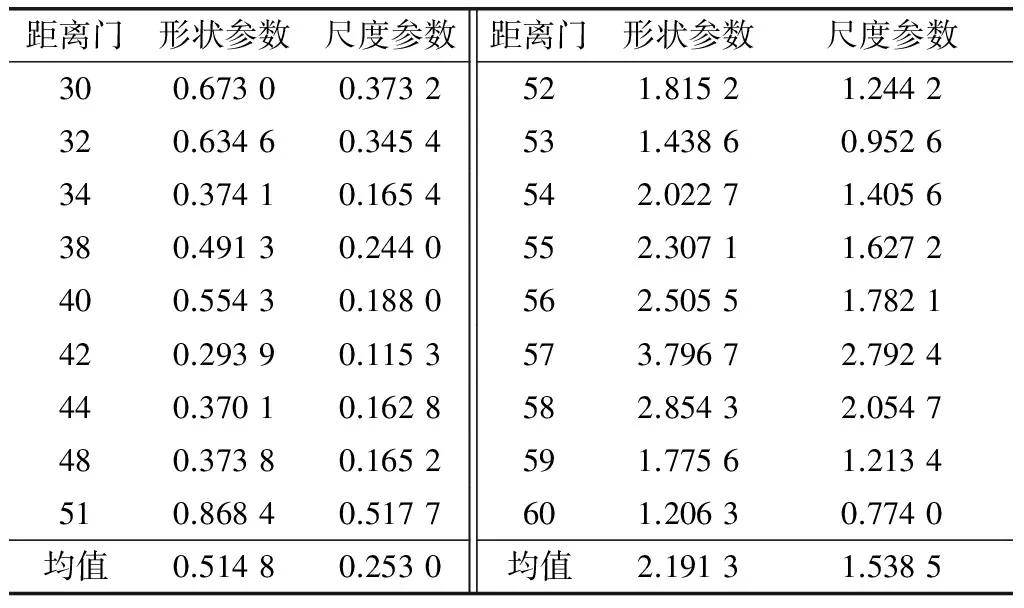
表1 K分布模型参数表

由表1可知，第30～51个距离门参数值很小且随距离门波动小,而第52～60个距离门参数值较大且随距离门波动大。这表明基于相位的地海杂波分割很好地对不同幅度分布特性的杂波进行了划分,从侧面验证了地海杂波分割结果的正确性。地海杂波分割结果作为对杂波环境的一种认知,为近岸杂波特性的分析及数据处理工作提供重要的参考依据。

3 结束语

岸基S波段雷达杂波的分析表明近岸回波中地物杂波的存在,地物杂波相对岸基雷达是静止的,而海杂波是动态变化的,基于此利用回波脉冲间相位差的大小判断散射体的运动状态,以此作为地海杂波分割的依据,实测数据分析结果表明该分割方法很好地划分了具有不同幅度分布特性的杂波。这对杂波特性的研究以及近岸海域目标检测性能的提升具有指导意义。

[1] MERRULL I S.雷达手册[M].第三版.南京电子技术研究所译.北京: 电子工业出版社, 2010: 579-584.

MERRULL I S. Radar Handbook[M]. 3rd ed. Nanjing electronic technology reseach institute. trans. Beijing: Publishing House of Electronics Industry, 2010: 579-584.

[2] 何友,黄勇,关键,等.海杂波中的雷达目标检测技术综述[J].现代雷达,2014,36(12):1-9.

HE Y, HUANG Y, GUAN J, et al. An overview on radar target detection in sea clutter[J]. Modern Radar, 2014, 36(12): 1-9.

[3] WARD K, WATTS S. Use of sea clutter models in radar design and development[J].IET Radar, Sonar & Navigation,2010,4(2):146-157.

[4] 丁昊,董云龙,刘宁波,等.海杂波特性认知研究进展与展望[J].雷达学报, 2016, 5(5): 499-516.

DING H, DONG Y L, LIU N B, et al. Overview and prospects of research on sea clutter property cognition[J]. Journal of Radars, 2016, 5(5): 499-516.

[5] DROSOPOULOS A.Description of the OHGR database[R]. Ottawa, Canada: Defence Research Establishment Ottawa, 1994.

[6] DONG Y, MERRETT D. Analysis of L-band multi-channel sea clutter[R]. Edinburgh, South Australia: Electronic Warfare and Radar Division, Defence Science and Technology Organisation, 2010：1-25.

[7] WEINBERG G. Investigation of the pareto distribution as a model for high grazing angle clutter[R]. Edinburgh, South Australia: Electronic Warfare and Radar Division, Defence Science and Technology Organisation, 2011：1-19.

[8] ROSENBERG L, WATTS S. High grazing angle sea-clutter literature review[R]. Edinburgh, South Australia: Electronic Warfare and Radar Division, Defence Science and Technology Organisation, 2013：1-31.

[9] ROSENBERG L. Sea-spike detection in high grazing angle X-band sea-clutter[R]. Edinburgh, South Australia: Electronic Warfare and Radar Division, Defence Science and Technology Organisation, 2013：1-19.

[10] 徐起. 海上战略预警能力与海工装备建设[J]. 中国工业评论, 2016, 9: 58-62.

XU Q. Maritime strategic early warning ability and the construction of marine engineering equipment[J]. China Industry Review, 2016, 9: 58-62.

[11] STOVE A G, ROBERTSON D A, MACFARLANE D G. Littoral sea clutter returns at 94 GHz[C]∥Proc.of the IEEE International Radar Conference, 2014: 1-6.

[12] WARD K D, TOUGH R J A. Modeling radar sea clutter in the littoral[C]∥Proc.of the IET Seminar on Radar Clutter Modeling, 2008: 25-31.

[13] STREMPEL M D, DE VILLIERS J P, CILLIERS J E, et al. A distribution analysis of segmented wave sea clutter in littoral environments[C]∥Proc.of the IEEE Radar Conference, 2015: 133-138.

[14] DANKLMAYER A, SIEGER S. Propagation experiment in the littoral at 94 GHz[C]∥Proc.of the IEEE International Symposium on Antennas and Propagation and USNC/URSI National Radio Science Meeting, 2015: 920-921.

[15] MONEY D G, BRANSON J, HOOKER M. Radar littoral environment pre-dictions and measurements[J].IEE Proceedings of Radar, 1997, 24(9):245-254.

[16] BRANSON J, WOODING S, DAWBER W N. Modeling of the littoral environment for real-time radar performance assessment[C]∥Proc.of the Radar,2002: 41-46.

[17] 万磊, 曾文静, 张铁栋, 等. 近海岸目标快速提取[J]. 哈尔滨工程大学学报, 2012, 33(9): 1158-1163.

WAN L, ZENG W J, ZHANG T D, et al. Fast extraction of offshore targets based on sea line detection[J]. Journal of Harbin Engineering University, 2012, 33(9): 1158-1163.