A Nontrivial Homotopy Element of Order p2Detected by the Classical Adams Spectral Sequence∗

Hao ZHAO Linan ZHONG

1 Introduction

Let p be an odd prime.Let A be the mod p Steenrod algebra and S be the sphere spectrum localized at p.Throughout the paper wefix q=2(p−1).To determine the stable homotopy groups of spheres π∗S is one of the central problems in homotopy theory.One of the main tools to approach it is the classical Adams spectral sequence(ASS)whose E2-term is given by(Z/p,Z/p)which is the cohomology of A.The Adams differential is given by

If a family of generators xi∈converges nontrivially in the ASS,then we obtain a family of homotopy elements fiin π∗S and we say that fihas filtration s and is represented by xi∈in the ASS.In order to compute π∗S by the ASS,it is critical to determine which element in the E2-terms survives to E∞.But so far not so much has been known about this.In known that only a0and h0in(Z/p,Z/p)survive to π∗S.They survive to the degree p map and the mod p Hopf invariant one element,respectively.By the Thom map(see[9]),it is shown that,,k0,a0h1(for p=3),bi(i≥0)and h0hn+2(n≥0)can survive to π∗S.Among them,,b0and k0survive to the degree p2map,thefirst periodic element α2,the secondary periodic elements β1and β2,respectively.In[2],R.Cohen showed that h0bn−1∈(Z/p,Z/p)survives to an element ζnin π∗S.

In[13],it was shown that the periodic elements detected by the Adams-Novikov spectral sequence are represented in the classical Adams spectral sequence as follows:

(1)For s/≡ 0 mod p,the first periodic elements αsis represented by

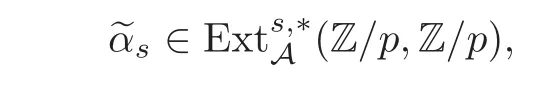
(2)For s/≡ 0,1 mod p,the second periodic elements βsis represented by

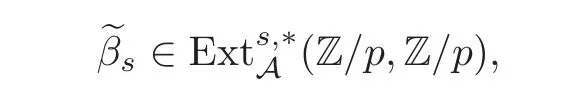
which is represented by s(s−1)h2,0h1,1in the May spectral sequence.

(3)For s/≡ 0,1,2 mod p,the third periodic elements γsis represented by

which is represented by s(s−1)(s−2)in the May spectral sequence.

Based on the representation of the periodic maps in ASS and R.Cohen’s elements ζnseveral non-trivial order p homotopy elements are detected(see[4–5,13]).But except for,all the non-trivial elements detected by the classical Adams spectral sequence are of order p.In this paper we will detect an order p2elementby the classical ASS.

Theorem 1.1Letpbe an odd prime.Then there exists a nontrivial element∈ π∗Sof orderp2,which is represented by(Z/p,Z/p)in the Adams spectralsequence andpis thefirst periodic elementαp.

Remark 1.1As shown in[9],when p=3,the element a0h1converges to an order p2homotopy elementof π∗S.Thus our result generalizes the case p=3 in[9]to the case of any odd prime.

This paper is organized as follows.In Section 2,we compute the generators of the E1-term of the May spectral sequence(MSS)which converge to the E2-term of the ASS.In Section 3,we give some higher May differentials related to Massey products.Then in Section 4 we give the proof of Theorem 1.1.

2 Computation via May Spectral Sequences

In this section we will recall the construction of cobar construction which connects the E2-terms of the ASS and the MSS.Let A∗denote the dual algebra of the mod p Steenrod algebra A.J.Milnor[10]showed that,as a Hopf algebra

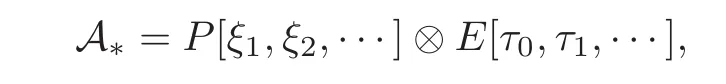
where P[]is the polynomial algebra and E[]is the exterior algebra.The secondary degrees of ξiand τiare 2(pi− 1)and 2(pi− 1)+1,respectively.The coproduct∆:A∗→ A∗⊗A∗is given by

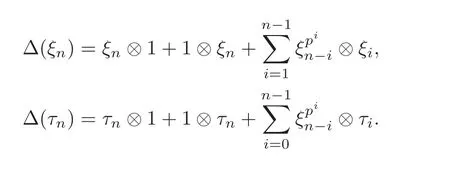
Let ε:A∗→ Z/p be the argumentation homomorphism and let A∗=Ker ε which is called the argumentation ideal of A∗.It then follows a bigraded cochain complex(C∗,∗(H∗S),d)=(C∗,∗(Z/p),d),where C∗,∗(Z/p)is the cobar construction with s-filtration

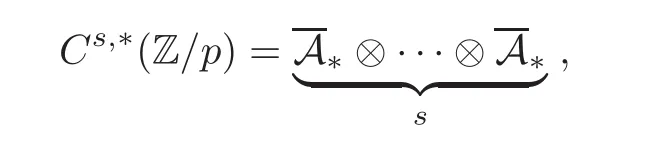
and the differential d:Cs,t(Z/p)→ Cs+1,t(Z/p)is given by

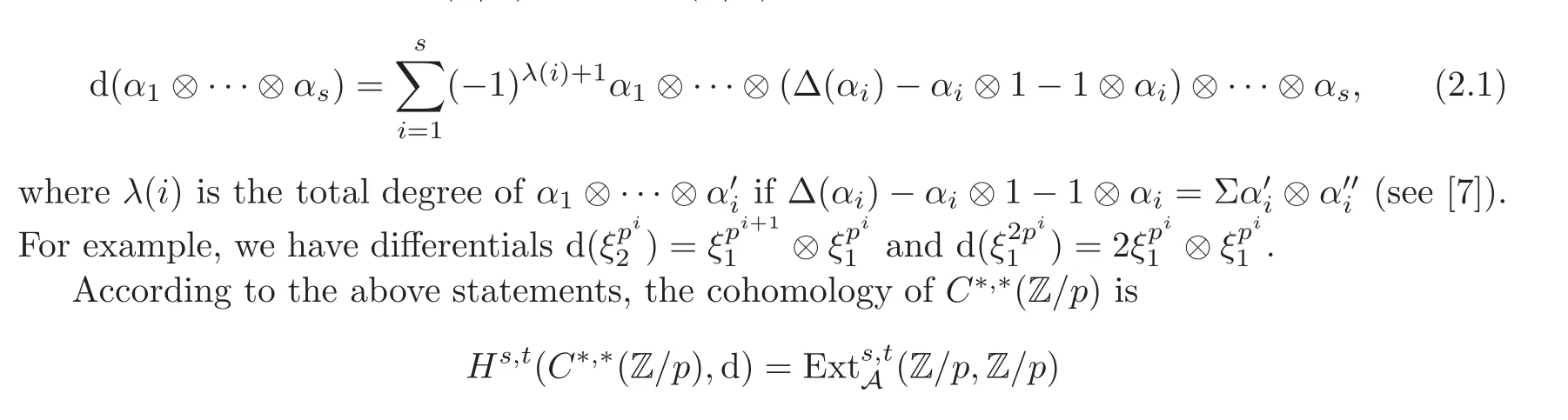
which is the E2term of the ASS. From [6], we know that

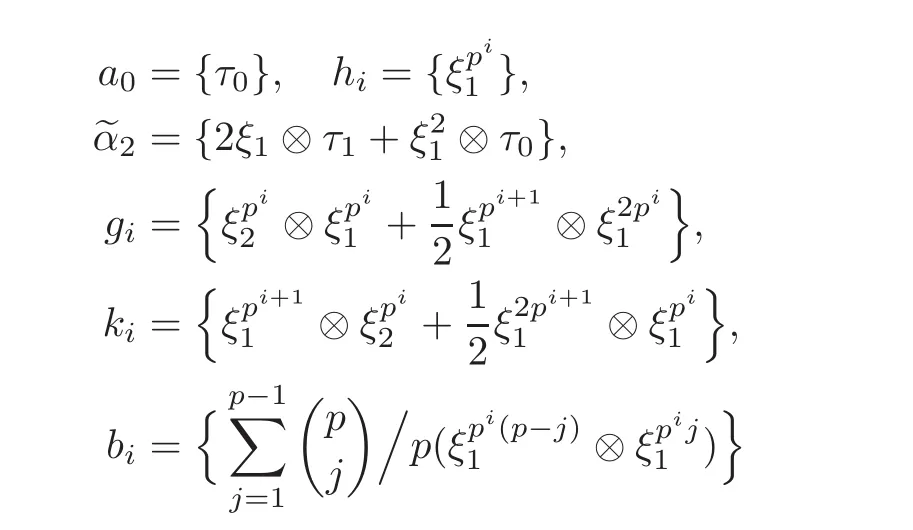
Based on [11, Theorem 3.2.5], we set a May filtration on A∗by M(τi−1)== 2i−1.It induces a corresponding filtration

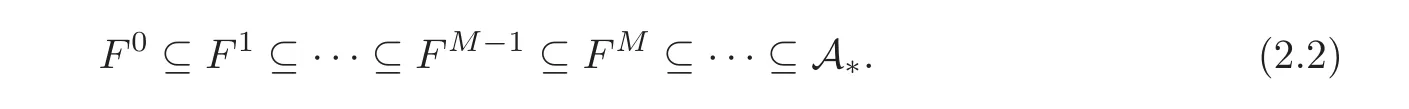
This shows that for the associated bigraded Hopf algebra

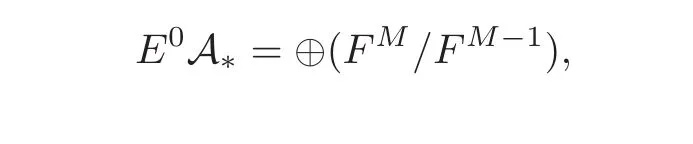
there is an isomorphism

where T[]denotes the truncated polynomial algebra of height p on the indicated generators,iand ξi,jare the projections of τiandrespectively. Applying the filtration (2.2) to the cobarconstruction C∗,∗(Z/p),we obtain a filtration

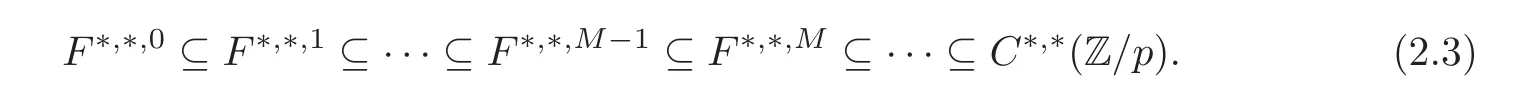
Then we have a tri-graded exact couple which induces the so-called May spectral sequence(MSS)

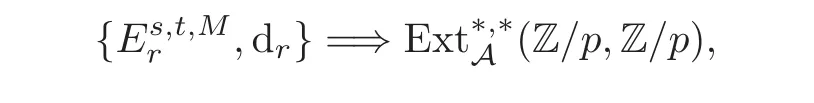
where dr:is the r-th differential of the MSS.Since the MSS converges to the E2-term of the ASS,to show the nontriviality of the elements in the Ext-group(Z/p,Z/p)is equivalent to showing that its representation in the MSS is an infinite cycle.This is the base of proving our main theorem.

The E0-term of the MSS is C∗,∗(E0A∗)= ⊕(F∗,∗,M/F∗,∗,M)and the E1-term E1=H∗(E0A∗,d0)is isomorphic to

where

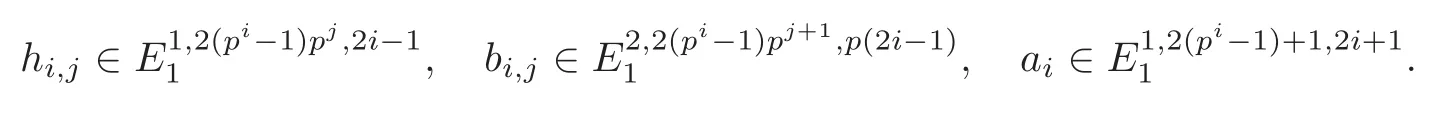
In thefiltrated cobar complexes,hi,j,bi,jand aiare represented by

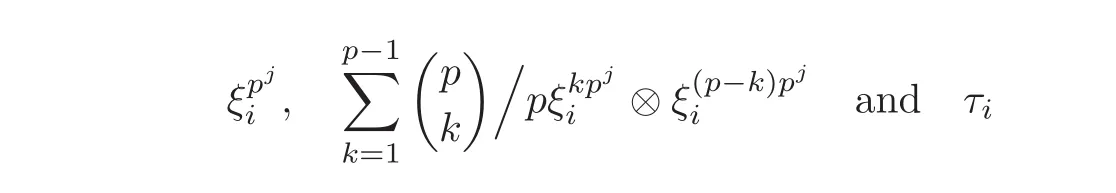
respectively.It is known that the generators h1,i,b1,iand a0converge to hi,bi,a0∈(Z/p,Z/p)respectively.

In the May spectral sequence,one has

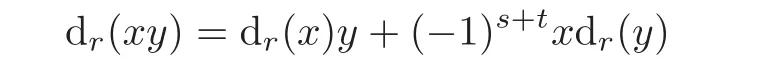
for x∈Es,t,∗r.The first May differential d1is given by

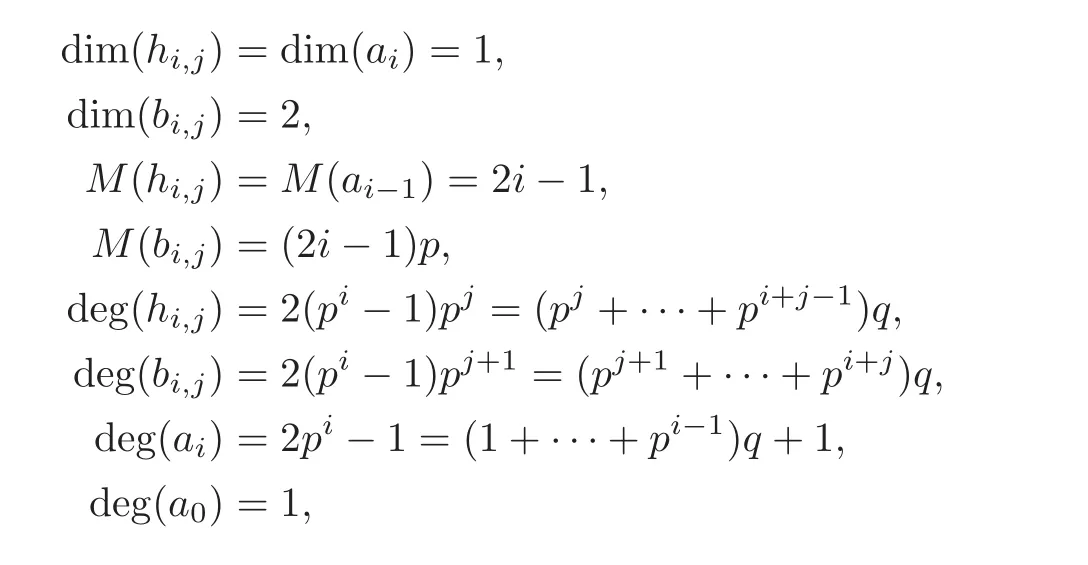
where i≥1 and j≥0.Now we consider the convergence of the elementSince a0converges to the degree p map in π∗S,in order to show thath1converges to a nontrivial element of order p2in π∗S,we plan to do it in two steps:(i)To show thath1andh1converge to two nontrivial elements in π∗S;(ii)To show thath1vanishes in the Adams spectral sequence.We will complete these two steps via the May spectral sequence.In what follows,we give some computation results which are needed to prove Theorem 1.1.

3 Higher May Differentials Related to Massey Products

Let us first recall the definition of Massey products.

Recalling from[8,Section 1],let R be a differential graded algebra.We assume that the differentials have degree+1 and d(x ·y)=d(x)·y+(−1)degxx ·d(y),where degx denotes the total degree of x.If V ∈ R,we define

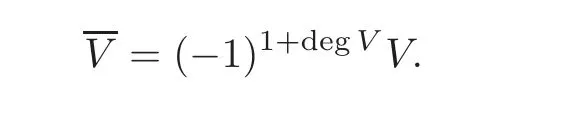
Let V and W be two elements in R or H(R).we have the following relations:

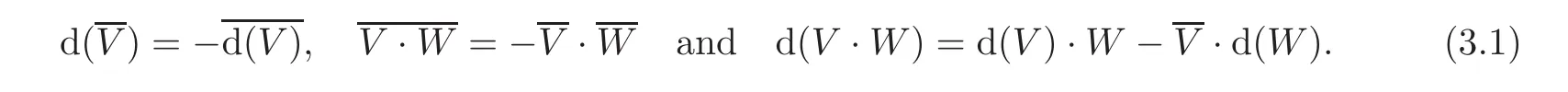
Let V1,V2,···,Vnbe a sequence of homologyclasses in H(R).Let Ai−1,i∈ R be a representative cycle for Vi,abbreviated{Ai−1,i}=Vi.Suppose thatVi+1=0.Then there exists Ai−1,i+1∈R such that d(Ai−1,i+1)=Ai−1,iAi,i+1and

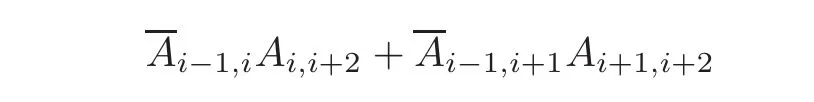
is a cycle in R,and we say that its homology class belongs to 〈Vi,Vi+1,Vi+2〉.

Inductively suppose that we get Ai,j∈R for 0≤i＜j≤n and(i,j)/=(0,n)such that

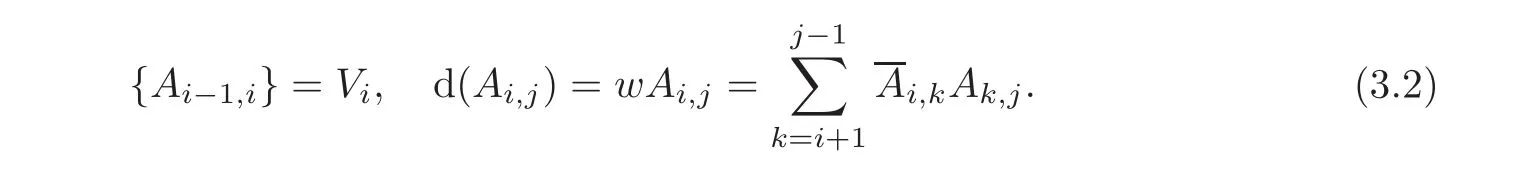
Then

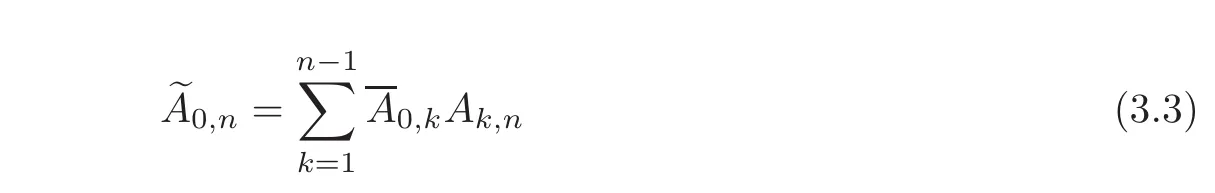
is a cycle in R.We say that{} ∈ 〈V1,V2···,Vn〉.

We say that the Massey product 〈V1,V2,···,Vn〉is defined if there exist Ai,j∈ R,0 ≤i＜ j ≤ n and(i,j)/=(0,n),which satisfies(3.2).The set of elements{Ai,j}is said to be a defining system for 〈V1,V2,···,Vn〉.We say that 〈V1,V2,···,Vn〉is strictly defined if each〈Vi,···,Vj〉,1 ≤ j−i≤ n−2 is defined and contains only the zero matrix.In particular,every defined triple product is strictly defined.

Consider the Massey product in the E1-term of the May spectral spectral sequence whereis a differential graded algebra.One has the following result.

Theorem 3.1 Ito nonzero scalar there is a nontrivial Maydifferentiald1:

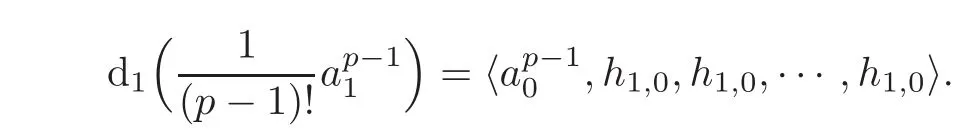
ProofAccording to the defining system of the Massey productin the E1-term of the May spectral sequence(see[7–8]),we obtainfrom d1(a1)=a0h1,0and h1,0·h1,0=0 in the E1-term of the May spectral sequence.Thus in the May spectral sequence,one has

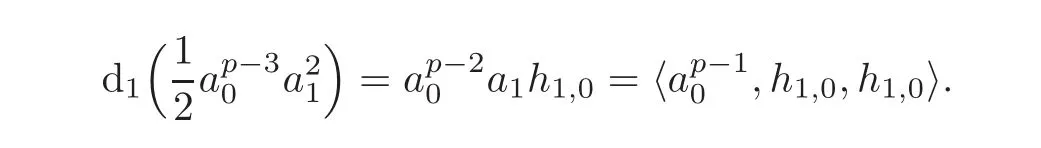
By induction one obtains

from the fact that the k-fold Massey product 〈h1,0,h1,0,···,h1,0〉=0 for k ＜ p.

4 Proof of Theorem 1.1

Before giving the proof of our main result,wefirst need two lemmas.

Lemma 4.1Letk=1or2.Then the elementnonzero.

Then it follows in Ext-group of the ASS that

Proof of Theorem 1.1For k=1 or 2,we have

which is nonzero due to Lemma 4.1.From Lemma 4.2,we see that the Adams differential

that converges to π∗S.By the method of infinite descent(see[3,11–12]),we get that

It is known that between the Brown-Peterson spectrum and the Eilenberg-MacLane spectrum,there is the Thom map Φ :BP → KZ/p which induces Φ:BP∗BP → A∗and the Thom map

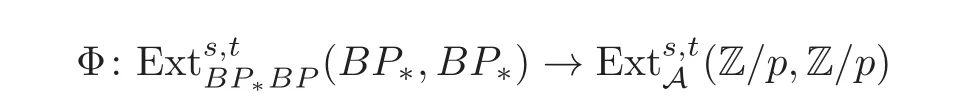
between the Adams-Novikov spectral sequence and the classical Adams spectral sequence.The map Φ:BP∗BP → A∗sends tiand vito ξiand zero,respectively.From the definition of thefirst periodic element,we know that

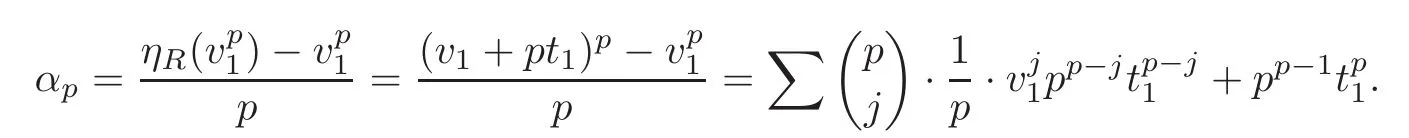
As we think:Except for the Thom map,there is a correspondence between the ANSS and the classical ASS where vi∈ BP∗corresponds to τiin the cobar complex of A.Based on this,we give a conjecture which is a general version of our results.

ConjectureIn the classical ASS,(Z/p,Z/p)converges to the pn+1order elementconverges to the first periodic element

AcknowledgementsThe authors would like to give their thanks to the referee for his/her many helpful suggestions on the original version of this paper,and they also acknowledge thefinancial support of the Institute for Mathematical Science during their stay at the National University of Singapore in August 2015.

[1]Aikawa,T.,3-dimensional cohomology of the mod p Steenrod algebra,Math.Scand.,47,1980,91–115.

[2]Cohen,R.,Odd Primary Families in Stable Homotopy Theory,Mem.Amer.Math.Soc.,30,Amer.Math.Soc.,Providence,1981.

[3]Hong,J.and Wang,X.,The secondary periodic element βp2/p2−1and its applications,Alg.Geom.Topol.,to appear.http://arxiv.org/pdf/1402.6074.pdf

[4]Liu,X.G.,A nontrivial product in the stable homotopy groups of spheres,Sci.in China,Ser.A,47,2004,831–841.

[5]Liu,X.and Wang,X.,A four-filtrated May spectral sequence and its applications,Acta Math.Sinica.,24,2008,1507–1524.

[6]Liulevicius,A.,The factorizations of cyclic reduced powers by secondary cohomology operations,Mem.Amer.Math.Soc.,42,1962,1–112.

[7]May,J.P.,The cohomology of restricted Lie algebras and of Hopf algebras,J.Algebra,3,1966,123–146.

[8]May,J.P.,Matric Massey products,J.Algebra,12,1969,533–568.

[9]Miller,H.R.,Ravenel,D.C.and Wilson,W.S.,Periodic phenomena in the Adams-Novikov spectral sequence,Ann.of Math.,106,1977,469–516.

[10]Milnor,J.,Steenrod algebra and its dual,Ann.of Math.,67,1958,150–171.

[11]Ravenel,D.C.,Complex Cobordism and Stable Homotopy Groups of Spheres,Academic Press,Orlando,1986.

[12]Ravenel,D.C.,The Adams-Novikov E2-term for a complex with p-cells,Amer.J.Math.,107,1978,933–968.

[13]Wang,X.and Zheng,Q.,The convergence ofh0hk,Sci.in China,Ser.A,41,1998,622–628.