A Boundary Schwarz Lemma for Holomorphic Mappings on the Polydisc∗

Yang LIUZhihua CHENYifei PAN

1 Introduction

The Schwarz lemma is known as one of the most important results in complex analysis.The Schwarz-Pick lemma is a variant of the Schwarz lemma,which essentially states that a holomorphic self-map of the unit disk decreases the distance of points in the Poincar´e metric.It has been generalized to the derivatives of arbitrary order in one complex variable(see[1–2]).Concerning several complex variables,Rudin[3]gave afirst derivative estimate for the bounded holomorphic functions on the polydisc,which is really a precursor to Schwarz-Pick estimate in high dimensions.Knese[4]studied the extremal problem for the holomorphic functions from the polydisk to the disk.Later,Liu[5]generalized the result of[1–2]to the holomorphic mappings on the unit ball and polydisc in Cn.

The Schwarz lemma at the boundary is another active topic in complex analysis(see[6]),which was applied to geometric function theory of one complex variable and several complex variables[7–10]as well as Hilbert space(see[11]).The following result is the classic boundary version of Schwarz lemma in one complex variable.

Theorem 1.1(see[6])LetDbe the unit disk inC,and letfbe the self-holomorphic mapping ofD.Iffis holomorphic atz=1withf(0)=0andf(1)=1,thenf′(1)≥ 1.

It is a well-known result that there are no biholomorphic mappings between Dnand Bn.Therefore,holomorphic mappings between Dnand Bnare interesting in several complex variables.There have been many results proved about such mappings since the 1970s(see[5,12–13]).Before giving the proof of the boundary version of Schwarz lemma for holomorphic mappings between Dnand BN,we give some notations and definitions first.

For a bounded domain V∈Cn,Cα(V)for 0＜α＜1 is the set of all functions f on V for which

is finite.Ck+α(V)is the set of all functions f on V whose kthorder partial derivatives exist and belong to Cα(V)for an integer k≥0.

Remark 1.1From the definition of the norm on Dn,the boundary points could be classified into several kinds.Let z0=(z1,···,zn)T∈ ∂Dn.If there are only r components of z0whose norm equals 1,then we denote the set of all this kind of boundary points by Er,1≤ r≤ n.It is easy to see that there are n different Erfor∂Dn,i.e.,

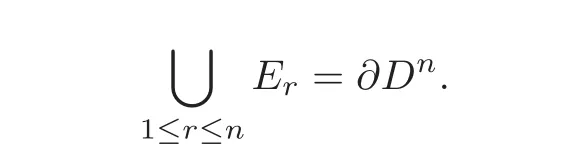
Especially,En=Tnwhich is the distinguished boundary of Dn.

In this paper,we study the mapping f∈H(Dn,BN)for any n,N≥1.Our main results are listed as follows.

Theorem 1.2Letf∈H(Dn,BN)for anyn,N≥1.Givenz0∈∂Dn,assumez0∈Erwith thefirstrcomponents at the boundary ofDfor some1≤ r≤ n.IffisC1+αatz0andf(z0)=w0∈ ∂BN,then there exist a sequence of nonnegative real numbersγ1,···,γr

whereλ =＞ 0,a=f(0)anddiagrepresents the diagonal matrix.

Remark 1.2Especially,when r=n,z0∈Tn.Denote bythe i-th column of identity matrix Inwith degree n.If z0∈Eris given by other expression such asare different from each other and ij∈ {1,···,n}for 1 ≤ j ≤ r.Then from the proof of the theorem,diag(γ1,···,γr,0,···,0)should be replaced by the diagonal matrix M with the ij-th row and ij-th column element M(ij,ij)= γij(j=1,···,r),otherwise being 0.

For r=1,we have the following corollary.

Corollary 1.1Letf∈H(Dn,BN)for anyn≥1.Givenz0∈E1⊂∂Dn,iffisC1+αatz0andf(z0)=w0∈ ∂BN,then there exists a real numberλ ∈ Rsuch that

whereλ ≥＞ 0anda=f(0).

For N=1,the following result is obtained.

Corollary 1.2Letf∈H(Dn,D)for anyn≥1.Givenz0∈∂Dn,assumez0∈Erwith thefirstrcomponents in the boundary ofDfor some1≤ r≤ n.IffisC1+αatz0andf(z0)=eiθ∈ ∂Dfor0 ≤ θ≤ 2π.Then there exist a sequence of nonnegative real numbers

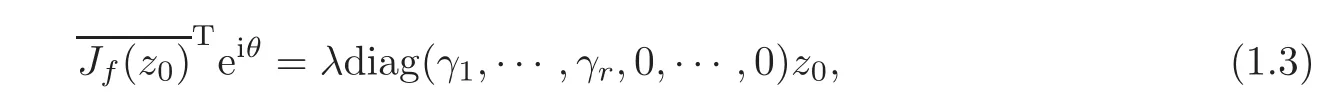
whereλ =＞ 0anda=f(0).

Remark 1.3This theorem is a general Schwarz lemma at the boundary for holomorphic mappings from the polydisc to the unit ball in any dimensions.For n=N=1,Corollary 1.1 gives Theorem 1.1 in[6].The smooth condition of f is C1+αat z0here.

The Kobayashi distances for the polydisc in Cnis given as follows(see[14]):

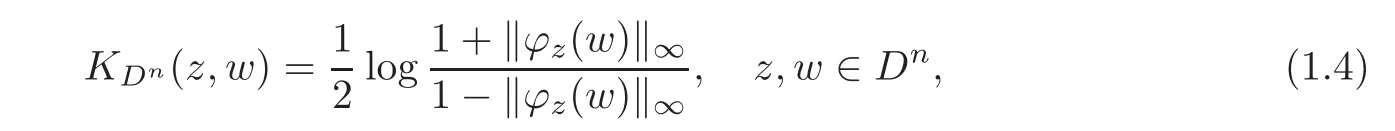
where ϕz(w)is the automorphism of Dngiven by

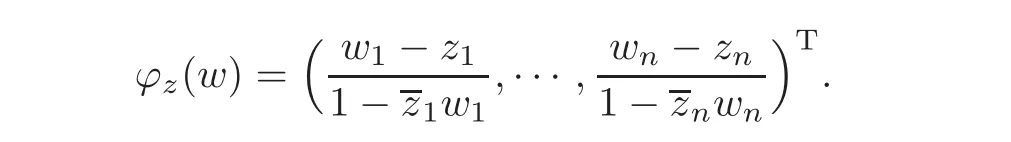
Meanwhile,the Kobayashi distances for the unit ball in CNcould be expressed by

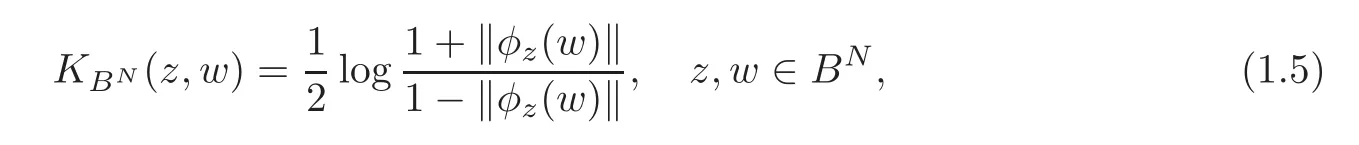
where φz(w)is the automorphism of BN,and

with Pzbeing the orthogonal projection of Cnby

and Qz(w)=w − Pz(w),as well as sz=It is found that φz(0)=z, φz(z)=0 and φz=.

It is the fact that the Kobayashi distance non-increases under holomorphic mappings(see[16]).Consider the mapping f ∈ H(Dn,BN)and f(0)=0.Then from(1.4)–(1.5),KBN(f(0),f(w))≤KDn(0,w),i.e.,

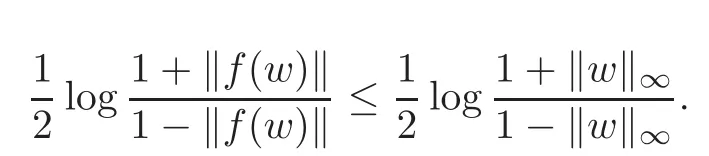
Lemma 1.1Assumef∈H(Dn,BN)for anyn,N≥1.Iff(0)=0,then

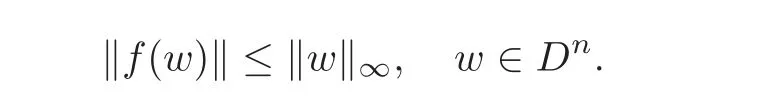
2 Proof of Theorem 1.2

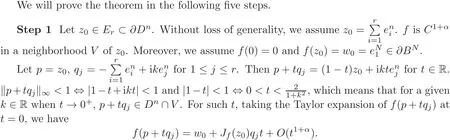
By Lemma 1.1,

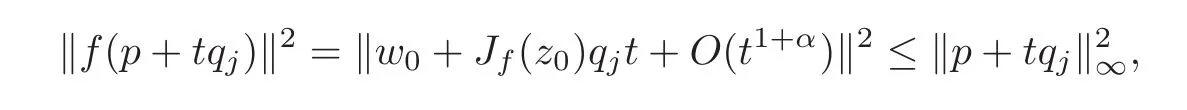
i.e.,

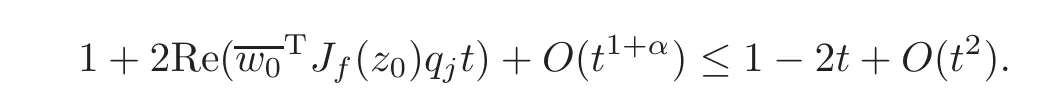
Substitute w0=and let t→0+,we have

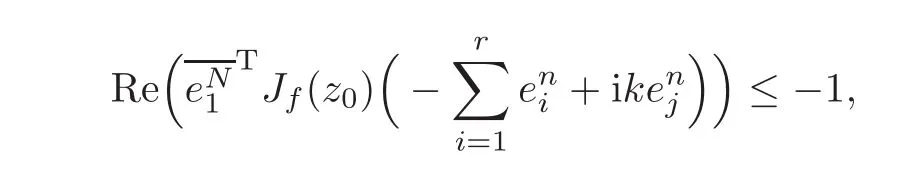
i.e.,

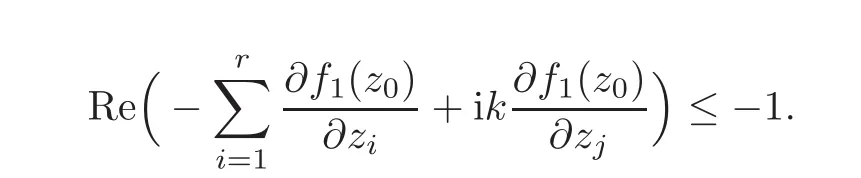
i.e.,

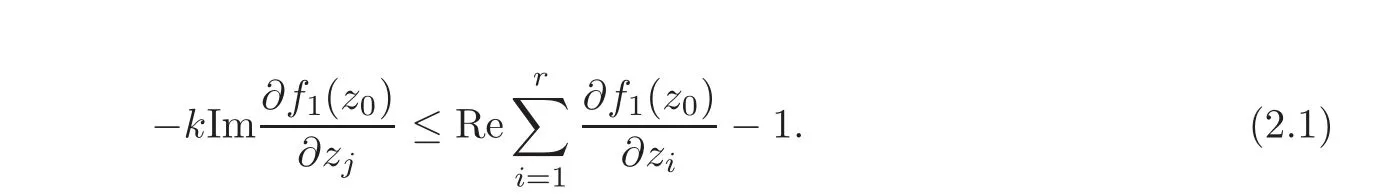
Since(2.1)is valid for any k∈R,so that

which gives

and

Step 2Let p=z0,qj=for 1≤j≤r and k≤0.Then p+tqj=(1−t)z0+for t∈ R.‖p+tqj‖∞＜ 1⇔ |1−t+kt|＜ 1 and|1−t|＜ 1⇔ 0＜ t＜which means that for any given k≤0,there are t→0+such that p+tqj∈Dn∩V.Taking the Taylor expansion of f(p+tqj)at t=0,we have

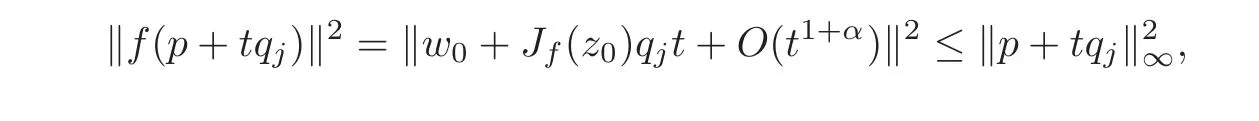
i.e.,

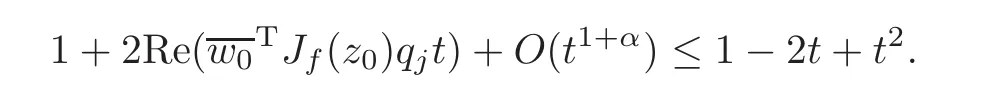
Substituting w0=and letting t→0+,we have

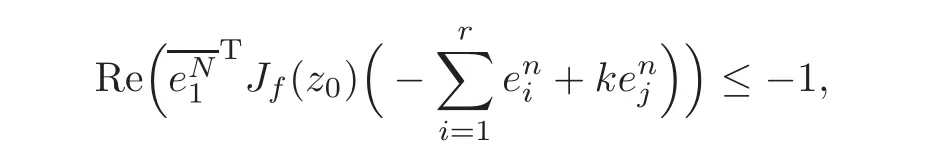
i.e.,

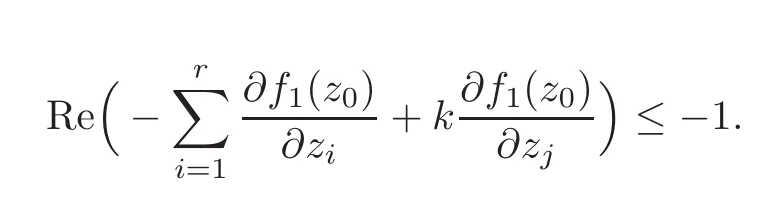
From(2.3),one gets

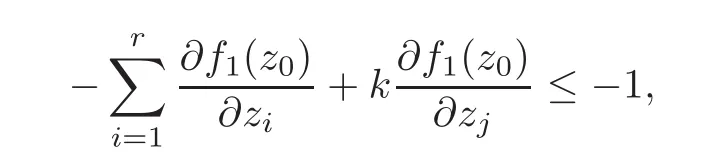
which is equal to

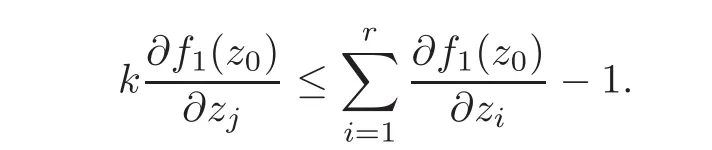
The right-hand side of the above inequality is nonnegative from(2.2)–(2.3).Since k ≤ 0 is arbitrary,it is obtained that

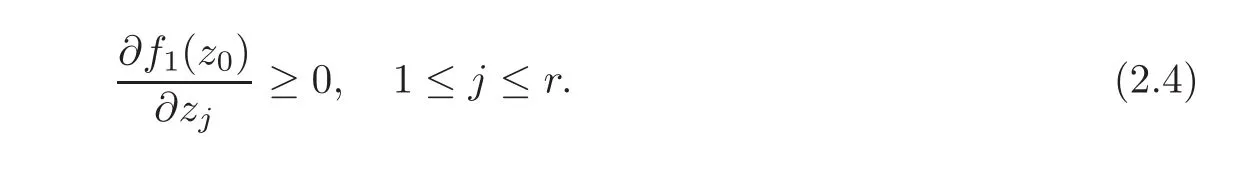
Step 3Let ql=for r+1≤l≤n and k/=0∈R.Then p+tql=for t∈ R.‖p+tql‖∞＜ 1⇔|1−t|＜1 and|ikt|2＜ 1⇔0＜ t＜ min,2.Therefore,given a k(/=0)∈R,there exist t→0+such that p+tq∈Dn∩V.Similarly,taking the Taylor expansion of f(p+tql)at t=0,we have

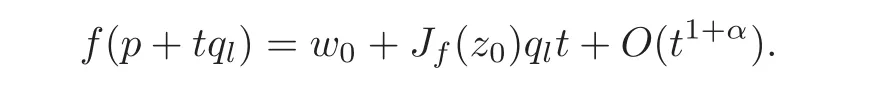
By Lemma 1.1,

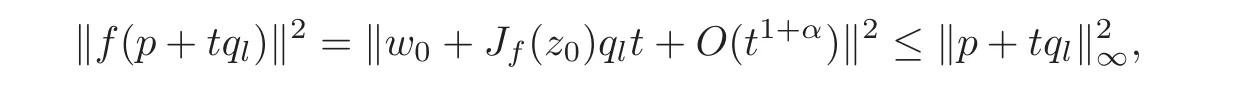
i.e.,

Substituting w0=and letting t→0+,we have

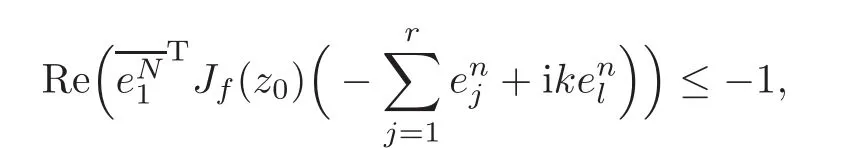
i.e.,

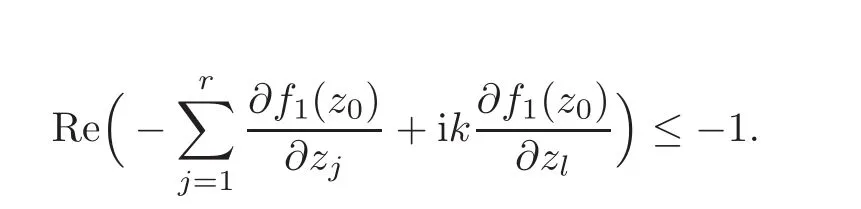
From the above inequality as well as inequality(2.3),one has

Since the right-hand side of the above inequality is a nonnegative scalar,with the similar argument to Step 1,we have

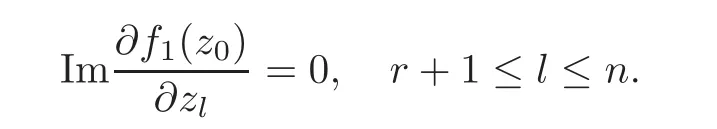
Meanwhile,if we assume p=z0,q=−for r+1≤l≤n and any k/=0∈R.It is easy tofind

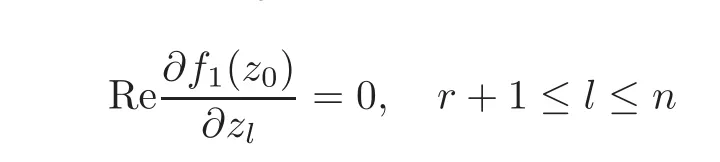
as well.Therefore,

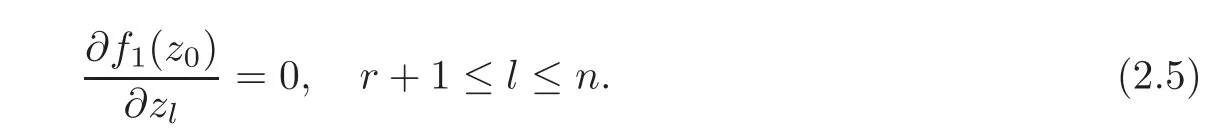
As a result of(2.2)and(2.4)–(2.5),we have

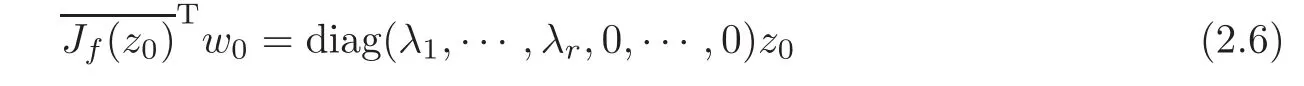
for w0=

Step 4Now let z0∈ Erbe any given point at∂Dnwith thefirst r components in the boundary of D,i.e.,z0is not necessaryThen there exists a special kind of diagonal unitary matrix Uz0such that Uz0(z0)=Assume f(0)=0,f(z0)=w0and w0is not

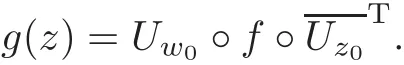
From Steps 2 and 3,we have

Step 5Let f(z0)=w0with z0∈ ∂Dn,w0∈ ∂BN.If f(0)=a/=0,then we use the automorphism of BNto get the result.Assume that φa(w)is an automorphism of BNsuch that φa(a)=0.Then φa(w0) ∈ ∂BNas well.With similar analysis to Step 3,there exists a Uφasuch that Uφa(φa(w0))=w0.Let

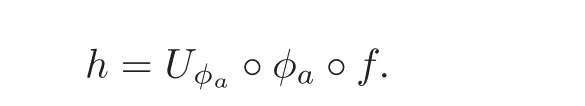
Then h(0)=0,h(z0)=w0.As a result from Step 4,there is a sequence of real numbers γj≥ 0≥ 1 such that

According to the expression of h,it is obtained that

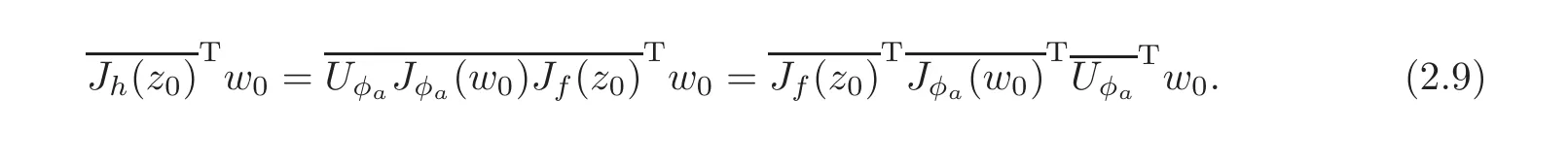
Since Uφa(φa(w0))=w0,we haveFrom the expression of the automorphism φagiven by[15],we have the following equality:

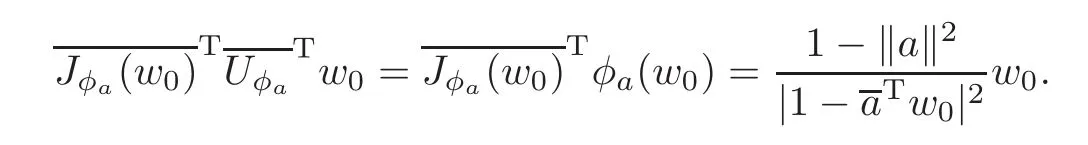
Therefore,combining with(2.9)we get

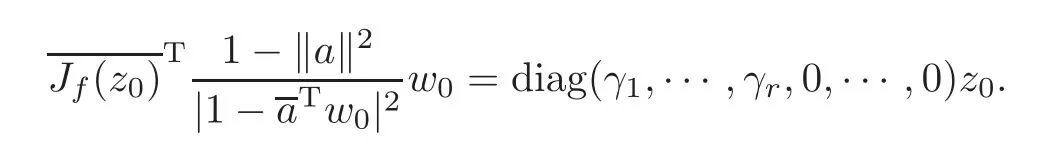
Consequently,

[1]Ruscheweyh,S.,Two remarks on bounded analytic functions,Serdica,11(2),1985,200–202.

[2]Dai,S.and Pan,Y.,Note on Schwarz-Pick estimates for bounded and positive real part analytic functions,Proceedings of the American Mathematical Society,136(2),2008,635–640.

[3]Rudin,W.,Function Theory in Polydiscs,W.A.Benjamin,New York,1969.

[4]Knese,G.,A Schwarz lemma on the polydisk,Proceedings of the American Mathematical Society,135(9),2007,2759–2768.

[5]Liu,Y.and Chen,Z.,Schwarz-Pick estimates for holomorphic mappings from the polydisk to the unit ball,Journal of Mathematical Analysis and Applications,376(1),2011,123–128.

[6]Garnett,J.,Bounded Analytic Functions,Academic Press,New York,1981.

[7]Krantz,S.,The Schwarz lemma at the boundary,Complex Variables and Elliptic Equations,56(5),2011,455–468.

[8]Liu,T.,Wang,J.and Tang,X.,Schwarz lemma at the boundary of the unit ball in Cnand its applications,Journal of Geometry Analysis,25(3),2015,1890–1914.

[9]Tang,X.,Liu,T.and Lu,J.,Schwarz lemma at the boundary of the unit polydisk in Cn,Science China Mathematics,58(8),2015,1639–1652.

[10]Liu,Y.,Dai,S.and Pan,Y.,Boundary Schwarz lemma for pluriharmonic mappings between unit balls,Journal of Mathematical Analysis and Applications,433(1),2016,487–495.

[11]Chen,Z.,Liu,Y.and Pan Y.,A Schwarz lemma at the boundary of Hilbert balls,Chin.Ann.Math.Ser.B,to appear.

[12]Alexander,H.,Holomorphic mappings from the ball and polydisc,Mathematische Annalen,209(3),1974,249–256.

[13]Alexander,H.,Extremal holomorphic imbeddings between the ball and polydisc,Proceedings of the American Mathematical Society,68(2),1978,200–202.

[14]Jarnicki,M.and Pflug,P.,Invariant distances and metrics in complex analysis,Walter de Gruyter,9,Berlin,1993.

[15]Rudin,W.,Function Theory in the Unit Ball of Cn,Springer-Verlag,New York,2009.

[16]Kobayashi,S.,Intrinsic metrics on complex manifolds,Bulletin of the American Mathematical Society,73(3),1967,347–349.