New Homogeneous Einstein Metrics on SO(7)/T∗

Yu WANGTianzeng LIGuosong ZHAO

1 Introduction

An important class of homogeneous manifolds is the orbits of the adjoint action of a semisimple compact Lie group,called generalizedflag manifolds.Such manifolds can be described by a quotient M=G/C(T),where C(T)is the centralizer of a torus T of the Lie group G.If C(T)=T,then M=G/T is called a fullflag manifold.

Invariant Einstein metrics on fullflag manifolds corresponding to classical Lie groups were studied by several authors(see[1–3]).Nevertheless when the isotropy summands of the fullflag manifolds increase,it is very difficult to find all the G-invariant Einstein metrics.Since the system of the Einstein equations is very complex,it is a non-trivial problem to get all the positive real solutions of the system of the Einstein equations.In this paper,we give the classification problem of homogeneous Einstein metrics on the fullflag manifold SO(7)/T,which admits precisely five Einstein metrics(up to isometry),where one is Kähler Einstein metric and four are non-Kähler Einstein metrics.

This paper is organized as follows.In Section 2 we recall the Lie theoretic description of a generalizedflag manifold G/K of a compact and connected semisimple Lie group G.In Section 3 we compute the non-zero structure constants of the fullflag manifold SO(7)/T and consider the isometric problem,then prove that SO(7)/T admitsfive(up to isometry)SO(7)-invariant Einstein metrics.

2 Generalized Flag Manifold

In this section we recall the Lie-theoretic description of M=G/K.

Let k and g be the Lie algebras of K and G respectively,and(·,·)be the Cartan Killing form on the Lie algebra g.Let gCand kCbe the complexifications of g and k respectively.The complexification ηCis a Cartan subalgebra of gC,where η is the Cartan subalgebra of g.

We denote by(ηC)∗the dual space of ηC,and let R ⊂ (ηC)∗be the root system of gCrelative

Set

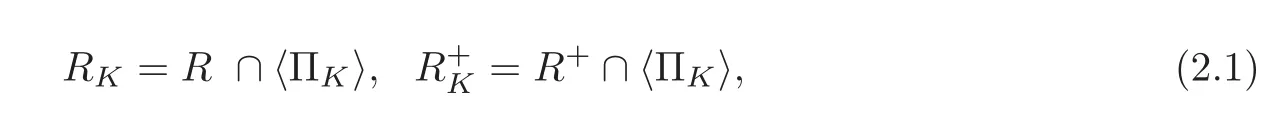
where〈ΠK〉denotes the set of roots generated by ΠK.Let RMbe a set such that R=RK∪RM,which is called the set of complementary roots of M.Then one can get

We choose a Weyl basis{Eα,Hα:α ∈ R}of gCwith(Eα,E−α)=1,[Eα,E−α]=Hαand

where the constants Nα,βsatisfy Nα,β= −N−α,−βand Nβ,α= −Nα,β.Then we obtain that

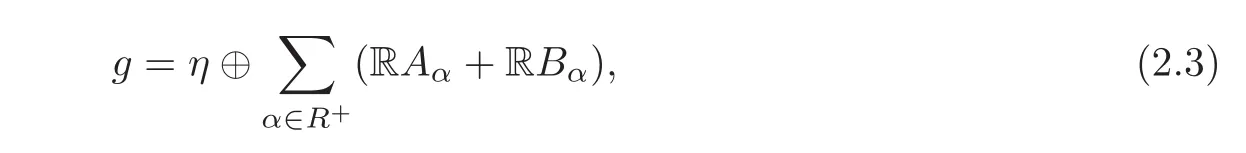
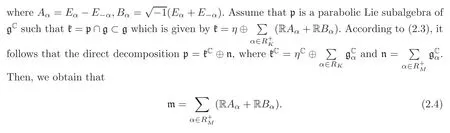
For convenience,we fix a system of simple roots Π ={α1,···,αr,φ1,···,φk}of R,so that ΠK={φ1,···,φk}is a basis of the root system RKand ΠM= ΠΠK={α1,···,αr}(r+k=l).We consider the decomposition R=RK∪ RM,and define the set

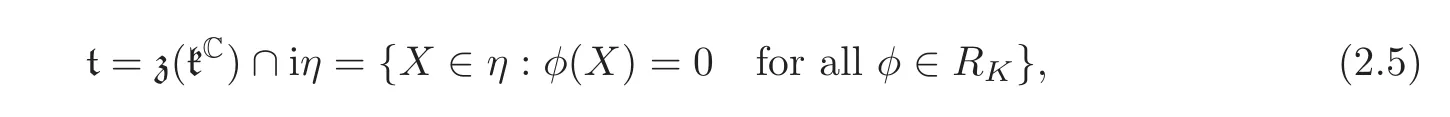
where η is the real ad-diagonal subalgebra η = ηC∩ ik,z presents the center of kC.Consider the linear restriction map κ :η∗→ t∗defined by κ(α)= α|t,and set Rt= κ(R)= κ(RM).The elements of Rtare called t-roots.Note that κ(RK)=0 and κ(0)=0.

Proposition 2.1(see[4–5])There is a one-to-one correspondence betweent-roots and complex irreduciblead(kC)-submodulesmξofmC.This correspondence is given by

ThusmCmξ.Moreover,these submodules are inequivalent asad(kC)-modules.

Since the complex conjugation τ:gC→gC,X+iY →X−iY(X,Y ∈ g)of gCwith respect to the compact real form g interchanges the root spaces,i.e.,τ(Eα)= −E−αand τ(E−α)=Eα,a decomposition of the real ad(k)-module m=(mC)τinto real irreducible ad(k)-submodule is given by

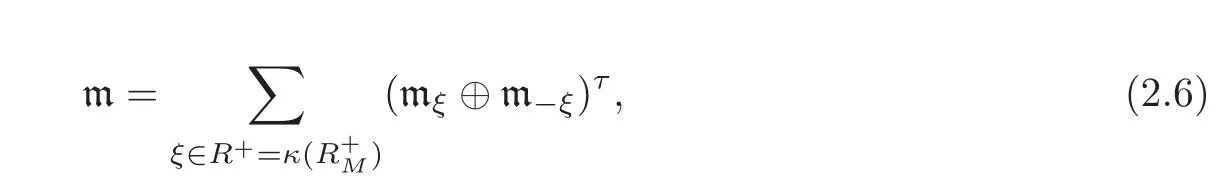
where nτdenotes the set of fixed points of the complex conjugation τ in a vector subspace n⊂gC.If,for simplicity,we setthen according to(2.6)each real irreducible ad(k)-submodule mi=(mξi⊕ m−ξi)τ(1 ≤ i ≤ s)corresponding to the positive t-roots ξiis given by

A t-root is called simple if it is not a sum of two positive t-root.Let ΠM= Π ΠK={α1,···,αr}.Then the set{αi= αi|t:αi∈ ΠM}is a t-base of t∗.

A G-invariant Riemannian metric g on M is identified with an Ad(K)-invariant inner product〈·,·〉on m,which can be written as〈X,Y 〉= −(ΛX,Y)(X,Y ∈ m),where Λ :m → m is an Ad(K)-invariant positive definite symmetric endomorphism on m.Due to the decompositionwhere each element in{xξ:ξ∈}is an eigenvalue of Λ.Due to decomposition(2.7),Λ is given by

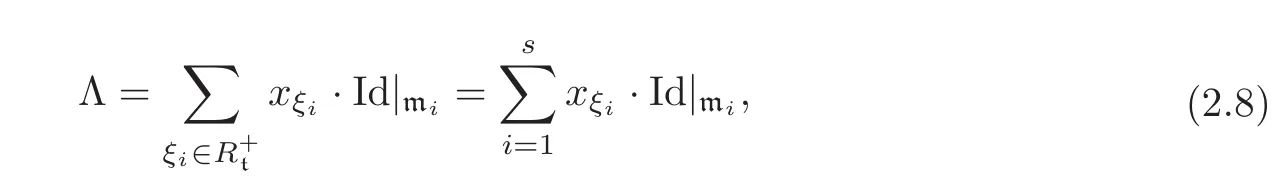
where xi≡ xξifor any

It is obvious that the vectors{Aα,Bα:α ∈}are eigenvectors of Λ corresponding to the eigenvalue xi≡ xξi.We also denote this eigenvalue by xα∈ R+,where α ∈is such that κ(α)= ξifor any 1 ≤ i≤ s.We extend Λ to mCwithout any change in notation.Hence the inner product g= 〈·,·〉admits a natural extension to an ad(kC)-invariant bilinear symmetric form on mC.Then the root vectors{Eα:α ∈ RM}are eigenvectors of Λ :mC→ mCcorresponding to the eigenvalues xα=x−α＞ 0.If we denote by{ωα}the basis of the dual space(mC)∗,which is dual to the basis{Eβ,β∈RM},i.e.,ωα(Eβ)=,then we obtain the proposition below.

Proposition 2.2(see[4,6])Every realad(kC)-invariant inner productg= 〈·,·〉onmChas the form

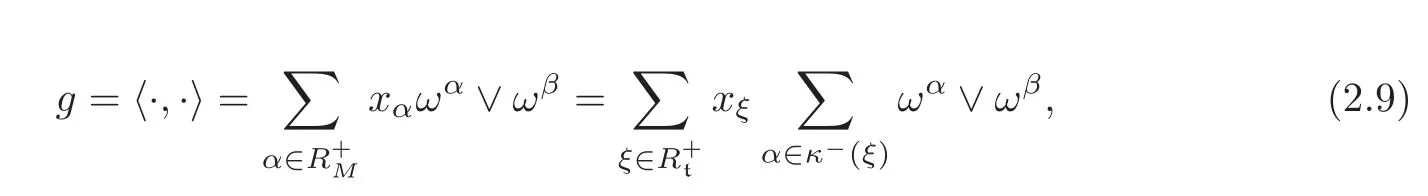
whereand the positive real numbersxαsatisfyxα=xβifα|t= β|tfor anyα,β ∈.

The space of G-invariant Riemannian metric g= 〈·,·〉= −(Λ·,·)on M is given by

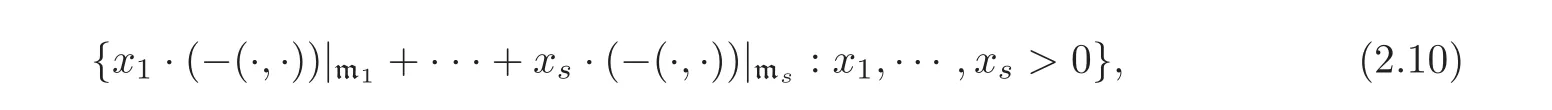
where x1≡ xξ1＞ 0,···,xs≡ xξs＞ 0.

Then the Ricci tensor Ricgof G/K(as a G-invariant symmetric covariant 2-tensor on G/K)is identified with an Ad(K)-invariant symmetric bilinear form on m given by

Here γ1,···,γsare the components of the Ricci tensor on each mi.

Proposition 2.3(see[7])Letg= 〈·,·〉be aG-invariant metric given by(2.10),andJbe aG-invariant complex structure induced by an invariant ordering.Then,gis a Kählerian metric with respect to the complex structureJ,if and only if the positive real numbersxξsatisfyxξ+ζ=xξ+xζfor anyξ,ζ,ξ+ ζ∈= κ().Equivalently,gis Kähler,if and only ifxα+β=xα+xβ,whereα,β,α + β ∈satisfyκ(α)= ξandκ(β)= ζ.

Let{eα}be an orthogonal basis with respect to −(·,·)adapted to the decomposition of m:eα∈ miand eβ∈ mjwith i＜ j then α ＜ β.Following[8],Aγα,β:= −([eα,eβ],eγ),thus

where the sum is taken over all indices α,β,γ with eα∈ mi,eβ∈ mj,eγ∈ mkand i,j,k ∈{1,···,s}.Hence ck

ijis nonnegative,symmetric in all the three entries,and is independent of the orthogonal basis chosen for mi,mjand mk(but it depends on the choice of the decomposition of m).

Now we introduce the notion of symmetric t-triples of t-roots.

Definition 2.1A symmetrict-triple int∗is a tripleΩ =(ξi,ξj,ξk)oft-rootsξi,ξj,ξk∈ Rtsuch thatξi+ ξj+ ξk=0.

Lemma 2.1(see[9])Let(ξi,ξj,ξk)be symmetrict-triples.Then there exist rootsα,β,γ ∈RMwithκ(α)= ξi,κ(β)= ξj,κ(γ)= ξksuch thatα + β + γ =0.

The calculus of the coefficientscan be laborious.However the next result shows exactly which of them are non-zero.

Lemma 2.2(see[7,Corollary 1.9])LetG/Kbe a generalizedflag manifold of a compact simple Lie groupGandRtbe the associatedt-root system.Assume thatm=m1⊕ ···⊕ msis a−(·,·)-orthogonal decomposition ofminto pairwise inequivalent irreduciblead(k)-module,and letξi,ξj,ξk∈ Rtbe thet-roots associated to the componentsmi,mjandmkrespectively.Then,/=0,if and only if(ξi,ξj,ξk)is a symmetrict-triples,i.e.,ξi+ ξj+ ξk=0.

3 Invariant Einstein Metrics on SO(7)/T

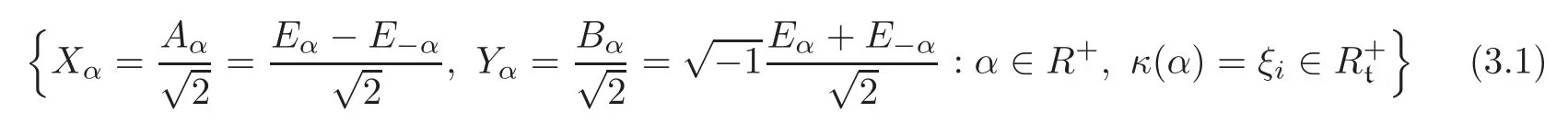
is a −(·,·)-orthogonal basis of mi.

Lemma 3.1(see[10,Proposition 1.3])The non-zero structure constantfor a fullflagmanifoldG/Tis given by

whereα,β ∈ R+withκ(α)= ξi, κ(β)= ξj, κ(α + β)= ξk.

Lemma 3.2(see[11])LetM=G/Kbe a reductive homogeneous space of a compact semisimple Lie groupGand letm=m1⊕ ···⊕ msbe a decomposition ofminto mutually inequivalent irreduciblead(k)-submodules.Then the componentsγ1,···,γsof the Ricci tensor of aG-invariant metric(2.10)onMare given by

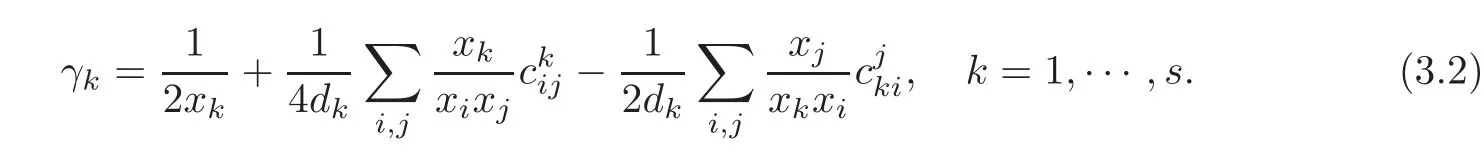
Next,we consider invariant Einstein metrics on the fullflag manifold of SO(7)/T with painted Dynkin diagraph

Lemma 3.3The non-zero structure constants of the fullflag manifoldSO(7)/Tare given byc412=c715=c816=c523=c928=c734=c635=c837=c946=c957=15.

ProofFrom the theory of Lie algebra,we can getwhere p,q are the largest nonnegative integers such that β+kα∈R with−p≤k≤q(see[12]).

假定一种利用人工智能技术进行肿瘤筛查的方法，包括以下步骤：获取影像数据、数据预处理、图像分割、边缘检测、肿瘤区域标记、基于预先训练的模型进行分类预测、自动生成筛查报告，为患者提供建议。这一方案显然满足疾病诊断方法的第一个构成要件“以有生命的人体为对象”，但是如果申请人在撰写专利申请文件时，为了规避疾病诊断方法的第二个构成要件而有意省略“自动生成筛查报告”的步骤，或者将这一步骤改写为：输出医学图像指标和相关预测参数以供医生进行诊断，此时，权利要求请求保护的方案是否属于以获得诊断结果为直接目的，结论就可能存在一定的争议。

By Lemma 3.1,we can calculate the non-zero structure constants of M as follows:

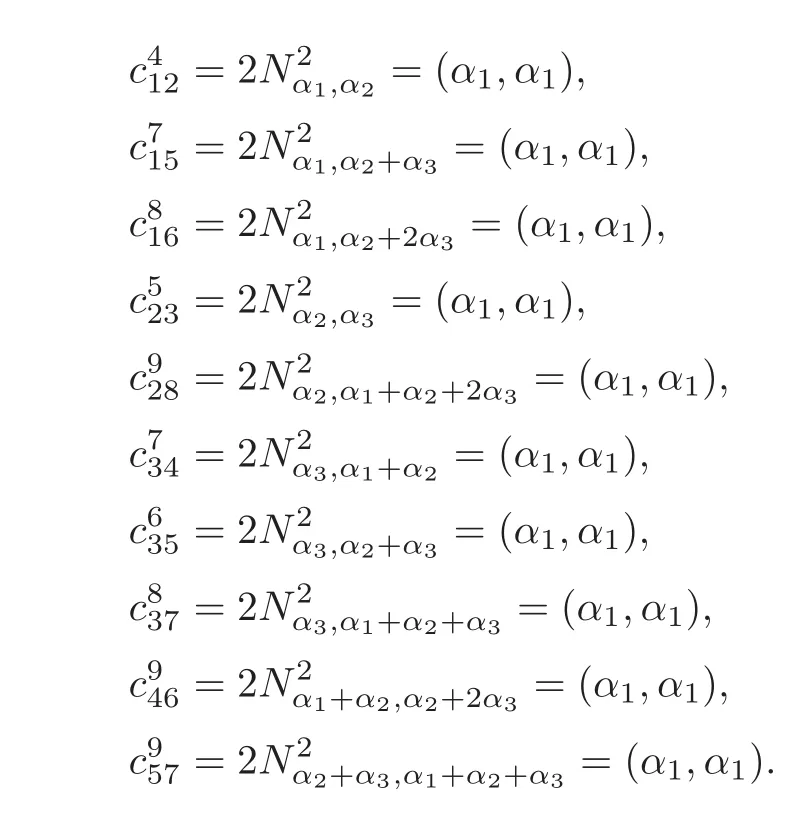
As(α1,α1)c957=15.

Lemma 3.4The componentsγi(i=1,···,9)of Ricci tensor associated to theSO(7)-invariant Riemmanian metricgonSO(7)/Tare the following:

ProofBy substituting the dimension di=dim(mi)=2 and the non-zero structure constantsinto(3.2),we can get the results.

A G-invariant Riemmanian metric g on M=SO(7)/T is Einstein,if and only if,there is a positive constant e such that γ1= γ2= γ3= γ4= γ5= γ6= γ7= γ8= γ9=e,or equivalently,

γ1− γ2= γ2− γ3= γ3− γ4= γ4− γ5= γ5− γ6= γ6− γ7= γ7− γ8= γ8− γ9=0. (3.3)By Lemma 3.4 and system(3.3),one can obtain the following polynomial system(we apply the normalization x1=1):

Every positive real solution x2＞0,x3＞0,x4＞0,x5＞0,x6＞0,x7＞0,x8＞0,x9＞0 of the system above determines a SO(7)-invariant Einstein metric(1,x2,x3,x4,x5,x6,x7,x8,x9)∈on M=SO(7)/T.With the help of computer we get all the forty-eight positive solutions(up to a scale)for above system,i.e.,there are forty-eight G-invariant Einstein metrics(up to a scale)on the fullflag manifold SO(7)/T.

Next we talk about the isometric problem about the metrics,in general,this is a non-trivial problem.

Let G/K be a generalized flag manifold with isotropy decomposition m=m1+···+ms,and d==dimM.For any G-invariant Einstein metric g=(x1,···,xs)on M,we determine a scale invariant given by Hg=Vd1Sg,where Sgis the scalar curvature of g,V=Vg/VBis the quotient of the volumesof the given metric g,and VBis the volume of the normal metric induced by the negative of the Killing form of G.We normalize VB=1,so

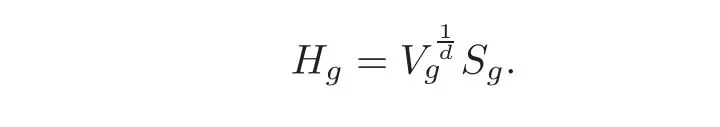
The scalar curvature Sgof a G-invariant metric g on M is given by the following well-known formula(see[8]):

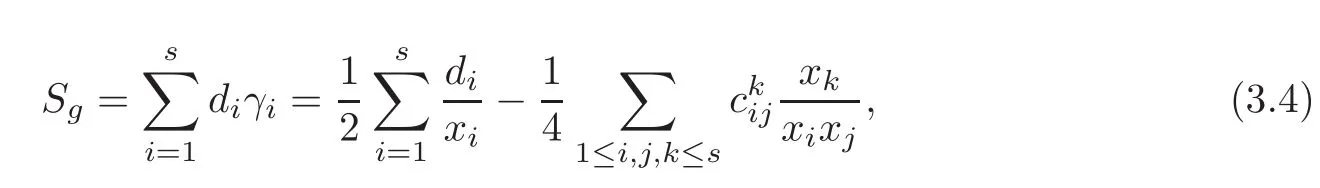
where the components γiof the Ricci tensor are given by(3.2).The scalar curvature is a homogeneous polynomial of degree− 1 on the variables xi(i=1,···,s).The volume Vgis a monomial of degree d,so Hg=Sgis a homogeneous polynomial of degree 0.Therefore,Hgis invariant under a common scaling of the variables xi.As

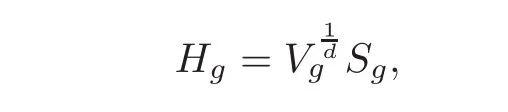
according to(3.4)we obtain

If two metrics are isometric,then they have the same scale invariant,so if the scale invariant Hgand Hg′are different,then the metrics g and g′can not be isometric.However,if Hg=Hg′,we can not immediately conclude if the metrics g and g′are isometric or not.For such a case we have to look at the group of automorphisms of G and check if there is an automorphism which permutes the isotopy summands and takes one metric to another.

Theorem 3.1The fullflag manifoldM=SO(7)/Tadmits(up to a scale)forty-eightSO(7)-invariant Einstein metrics,which approximately are given as follows:

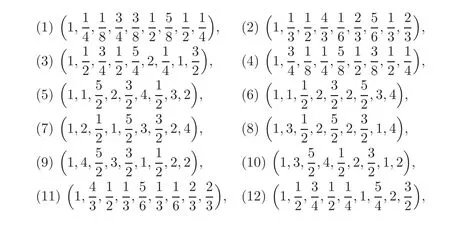
where(1),···,(24)are Kähler Einstein metrics.Then,the approximateHgcorresponding to every metricgfrom(1)to(48)are as follows:

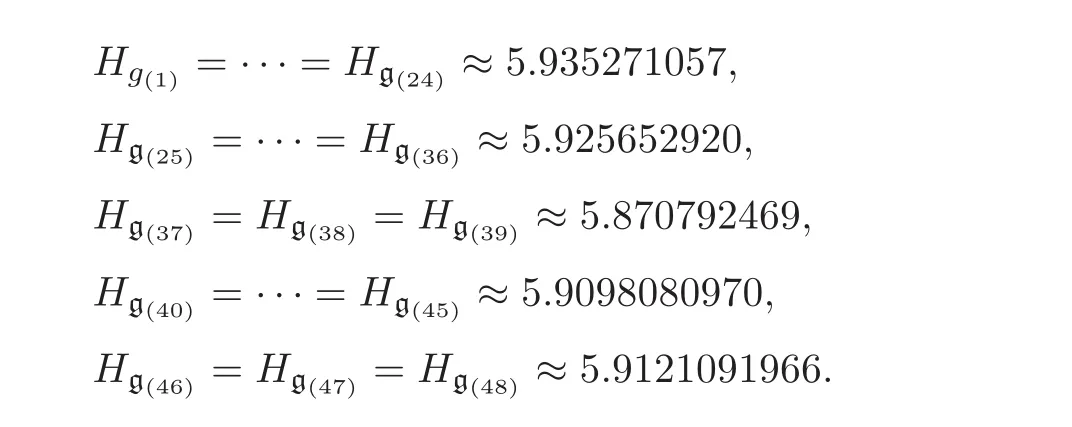
As it is known that there is a one-to-one correspondence between non-equivalent G-invariant complex structures and the non-isometric Kähler Einstein metrics on a flag manifold.Since there is only one G-invariant complex structure on any fullflag manifold,so there is only one non-isometric Kähler Einstein metric on fullflag manifold SO(7)/T,thus the Kähler Einstein metrics from(1)to(24)in Theorem 3.1 are all isometric.

By Theorem 3.1 we obtain that there are four non-equal values of Hgcorresponding to non-Kähler-Einstein metrics from(25)to(48).Thus there are at least four non-isometric non-Kähler Einstein metrics.Next,we prove there are exactly four non-isometric non-Kähler Einstein metrics.

Let

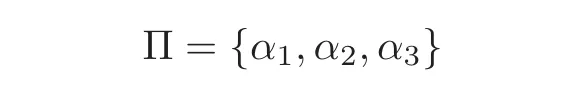
be the simple root system of the Lie algebra of SO(7).then the Weyl group W of SO(7)is generated by rα1,rα2,rα3,where

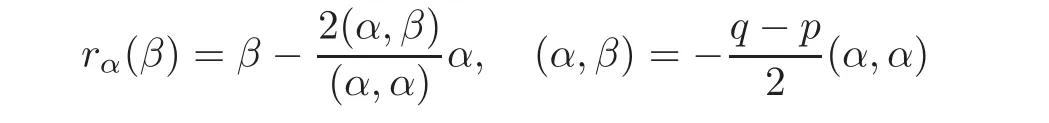
and p,q are the largest nonnegative integers such that β +kα ∈ R with

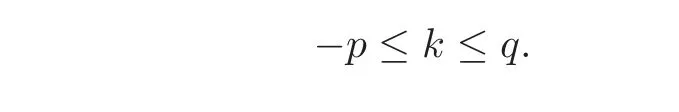
Let

be the positive roots of the Lie algebra of SO(7).Then we obtain

Since the action of the Weyl group of SO(7)on the root system of the Lie algebra SO(7)induces an action on the components of the SO(7)-invaraint metric

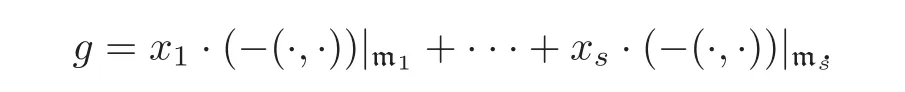
In particular,if

is a positive solution of the system of the Einstein equations of SO(7)/T,then

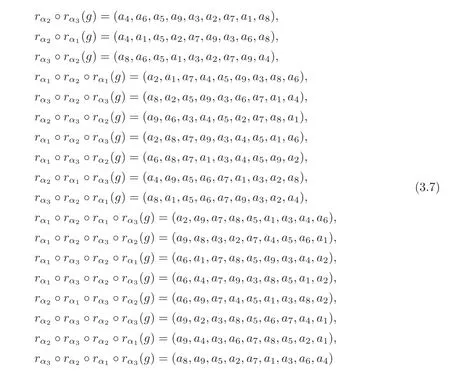
are also positive solutions of the system of the Einstein equations of the fullflag manifold SO(7)/T.These metrics in system(3.7)are all isometric,and they are all isometric to the metric g=(x1,x2,x3,x4,x5,x6,x7,x8,x9).

As for any G-invariant Einstein metric g,we have

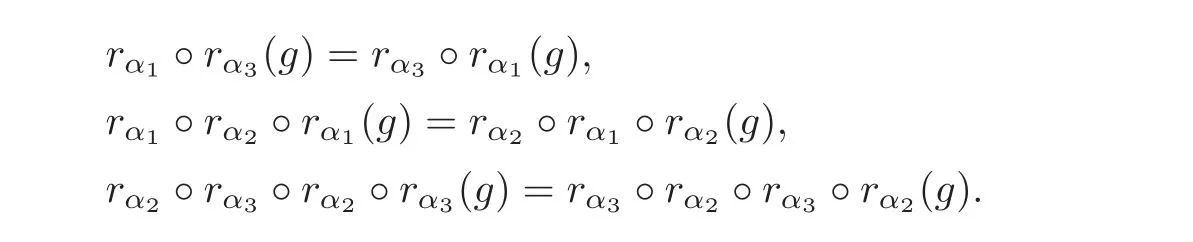
Thus,if g=(x1,x2,x3,x4,x5,x6,x7,x8,x9)is a G-invariant Einstein metric,w(g)is one of in system(3.7)for any w∈W(except the identity element Id).

As Hg(25)=Hg(26)= ···=Hg(36)=5.925652920,we prove that the metrics from(25)to(36)are isometric.

Because

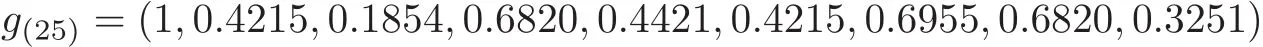
is a G-invariant Einstein metric,by the action of the elements of the Weyl group of SO(7)on g(25)(except the identity element Id),we can obtain 23 positive solutions in system(19).But some of them are equal,except the equal solutions we can get the metrics from(26)to(36),and they are all isometric to g(25)=(1,0.4215,0.1854,0.6820,0.4421,0.4215,0.6955,0.6820,0.3251).

As Hg(37)=Hg(38)=Hg(39)=5.870792469,we prove that the metrics from(37)to(39)are isometric.

Because g(37)=(1,0.6083,1.0188,1,1.0188,0.6083,0.2736,1,1)is a G-invariant Einstein metric,by the action of the elements of the Weyl group of SO(7)on g(37)(except the identity

map Id),we can obtain 23 positive solutions in system(3.7),but only two of them are not equal to each other.Thus we obtain the metrics(38)and(39),and they are all isometric to g(37)=(1,0.6083,1.0188,1,1.0188,0.6083,0.2736,1,1).

As Hg(40)= ···=Hg(45)=5.9098080970,we prove that the metrics from(40)to(45)are isometric.

Because

is a G-invariant Einstein metric,by the action of the elements of the Weyl group of SO(7)on g(40)(except the identity map Id),we can obtain 23 positive solutions in system(3.7),but onlyfive of them are not equal to each other.Thus we obtain the metrics from(41)to(45),and they are all isometric to g(40)=(1,0.6638,0.2309,0.6638,0.6826,0.6638,0.6826,0.6638,0.5983).

As Hg(46)=Hg(47)=Hg(48)=5.9121091966,we prove that the metrics from(46)to(48)are isometric.

Because g(46)=(1,0.7739,0.2818,0.7739,0.7978,0.7739,0.7978,0.7739,1)is a G-invariant Einstein metric,by the action of the elements of the Weyl group of SO(7)on g(46)(except the identity map Id),we can obtain 23 positive solutions in system(3.7),but only two of them are not equal to each other.Thus we obtain the metrics(47)and(48),and they are all isometric to g(46)=(1,0.7739,0.2818,0.7739,0.7978,0.7739,0.7978,0.7739,1).

By the analysis above it follows that there are exactlyfive non-isometric Einstein metrics on the fullflag manifold SO(7)/T,of which one is Kähler Einstein metric and four are non-Kähler Einstein metrics.

Theorem 3.2The fullflag manifoldSO(7)/Tadmits exactlyfiveSO(7)-invariant Einstein metrics(up to isometry).There is a unique Kähler Einstein metric(up to a scale)given byg=1,1,,2,,2,,3,4and other four are non-Kähler Einstein metrics(up to a scale)given by as follows:

(a)(1,0.4215,0.1854,0.6820,0.4421,0.4215,0.6955,0.6820,0.3251),

(b)(1,0.6083,1.0188,1,1.0188,0.6083,0.2736,1,1),

(c)(1,0.6638,0.2309,0.6638,0.6826,0.6638,0.6826,0.6638,0.5983),

(d)(1,0.7739,0.2818,0.7739,0.7978,0.7739,0.7978,0.7739,1).

[1]Arvanitoyeorgos,A.,New invariant Einstein metrics on generalizdflag manifolds,Trans.Amer.Math.Soc.,337(2),1993,981–995.

[2]Sakane,Y.,Homogeneous Einstein metrics on flag manifold,Lobachevskii J.Math.,4,1999,71–87.

[3]Dos Santos,E.C.F.and Negreiros,C.J.C.,Einstein metrics onflag manifolds,Revista Della,Uni´on Mathem´atica Aregetina,47(2),2006,77–84.

[4]Alekseevsky,D.V.and Perelomov,A.M.,Invariant Kähler-Einstein metrics on compact homogeneous spaces,Funct.Anal.Appl.,20(3),1986,171–182.

[5]Siebenthal,J.,Sur certains modules dans une alg´ebre de Lie semisimple,Comment.Math.Helv.,44(1),1964,1–44.

[6]Alekseevsky,D.V.,Homogeneous Einstein metrics,Differential Geometry and Its Applications(Brno Conference Proceedings),1987,1–21.

[7]Chrysikos,I.,Flag manifolds,symmetric t-triples and Einstein metrics,Differential Geom.Appl.,30(6),2012,642–659.

[8]Wang,Y.and Ziller,W.,Existence and non-excistence of homogeneous Einstein metrics,Invent.Math.,84,1986,177–194.

[9]Graev,M.M.,On the number of invariant Eistein metrics on a compact homogeneous space,Newton polytopes and contraction of Lie algebras,Int.J.Geom.Methods Mod.Phys.,3(5–6),2006,1047–1075.

[10]Arvanitoyeorgos,A.,Chrysikos,I.and Sakane,Y.,Homogeneous Einstein metrics on G2/T,Proc.Amer.Math.Soc.,14(7),2013,2485–2499.

[11]Park,J.S.and Sakane,Y.,Invariant Einstein metrics on certain homogeneous space,Tokyo J.Math.,20(1),1997,51–61.

[12]Varadarajan,V.S.,Lie Group,Lie Algebra and Their Representations,Springer-Verlag,New York,Berlin,Heidelberg,Tokyo,1984.

[13]Onishchik,A.L.and Vinberg,E.B.,Lie Groups and Lie Algebras III,Structure of Lie Groups and Lie Algebras,Springer-Verlag,Berlin,Heideberg,1994.