Quenching Phenomenon for a Parabolic MEMS Equation

Qi WANG

1 Introduction

We consider the parabolic problem

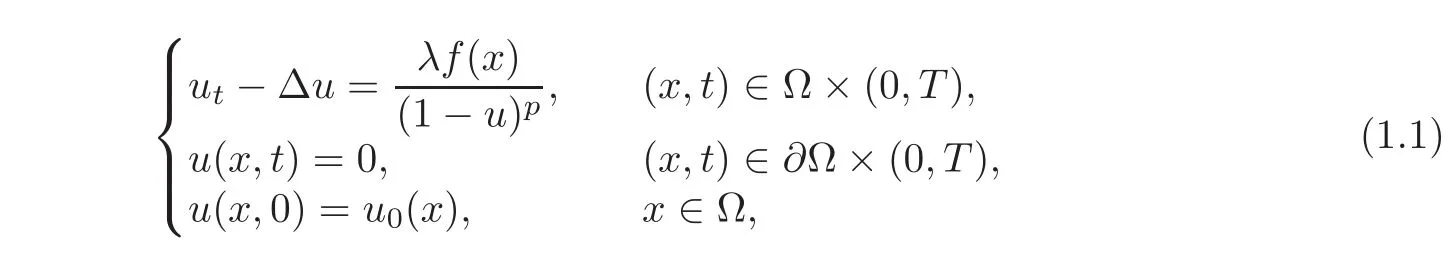
where p＞1,λ＞0,Ω is a smooth bounded domain in RN,f is a nonnegative bounded smooth function,u0(x)∈ [0,1)is a smooth function and u0(x)=0 on∂Ω.The associated stationary equation is as follows:

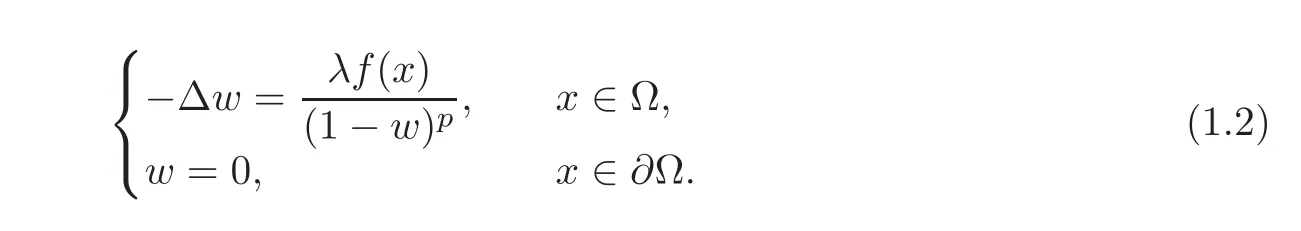
The problem(1.1)arises in the study of micro-electromechanical system devices.The parameter λ＞0 is a constant which is increasing with respect to the applied voltage(see[13,19]for more details).These systems are microsize integrated devices or tiny systems that combine mechanical and electrical components.They are used in systems ranging across automotive,medical,electronic,chemistry,biology,communication and defence applications.Recently,a mathematical modeling proposed by Pelesko and Bernstein[18]in 2002 leads to elliptic and parabolic PDEs of second or fourth order.In these lectures,some interesting problems,results and open questions have been presented on the MEMS modeling.We can refer to[7–8,13,16,18–19]and the references therein for detailed discussions on MEMS devices modeling.

We say that the solution w to(1.2)is regular or classical,if‖w‖∞＜ 1;the solution w to(1.2)is singular,if‖w‖∞=1.It is well known(see[3,10–11,22]and the references therein)that for any given f,there exists a critical value λ∗＞ 0 such that if λ ∈ (0,λ∗),the problem(1.2)has a unique stable classical solution wλand the solution to(1.1)is global with u0=0.Moreover,wλis the minimal solution and λ → wλis increasing.Here the minimal solution means that wλ≤ v for any solution v to(1.2).For λ = λ∗,the problem(1.2)admits a unique weak solution w∗:wλ,called the extremal solution,in the sense that

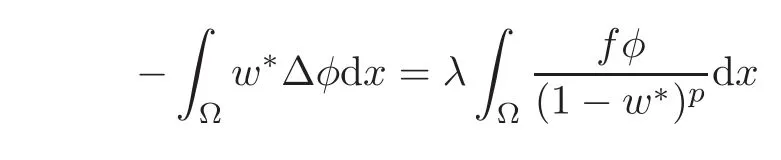
is nonnegative.While for λ ＞ λ∗,no solution to(1.2)exists,and with any u0satisfying‖u0‖∞＜ 1 the solution u to(1.1)reaches the value 1 at a finite time T∗,called quenching time;i.e.,the so called quenching or touchdown phenomenon occurs.More precisely,‖u(·,t)‖∞＜ 1=1.We say that the solution u to(1.1)quenches if it reaches 1 at a finite time.The more precise definition of the quenching time T∗is

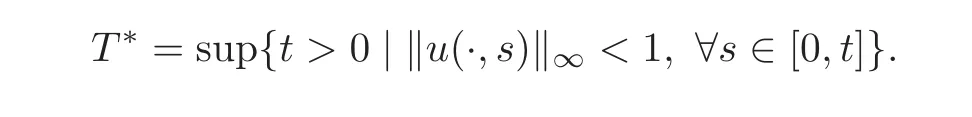
The corresponding quenching set is defined as

From[22],it can be deduced that

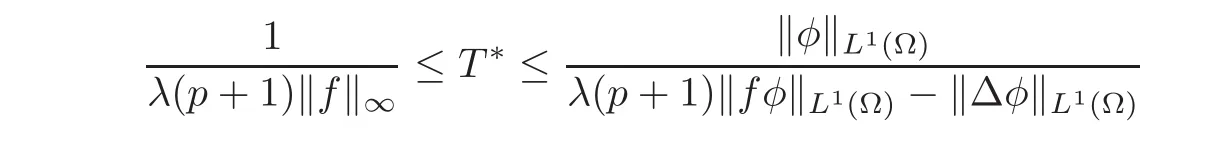
for large λ,where φ is any nonnegative C2function such that fφ /≡ 0 and φ =0 on ∂Ω.

In general,we know that w∗could be regular or singular.Usually,w∗is a regular solution in lower dimension and becomes singular in higher dimension(see[7,10]).

For general u0/≡ 0,it is known in[3,20]that if λ ＜ λ∗, ‖u0‖∞＜ 1,then there exists a unique solution u(x,t)to(1.1)which converges pointwise to its unique minimal steady-state w as t→+∞,provided that u0≥0 is a subsolution of(1.2).Furthermore,u(x,t)is monotone nondecreasing for t＞0.It is essential to understand the quenching phenomenon,such as the quenching set,the rate or asymptotic behavior of the quenching time T∗.Some interesting results have been obtained in several recent works(see for instance[9,11–12,21]and the references therein).In[9,21],we know that if w∗is regular,there exists an eigenfunction φ∗of Lw∗,λ∗,satisfying

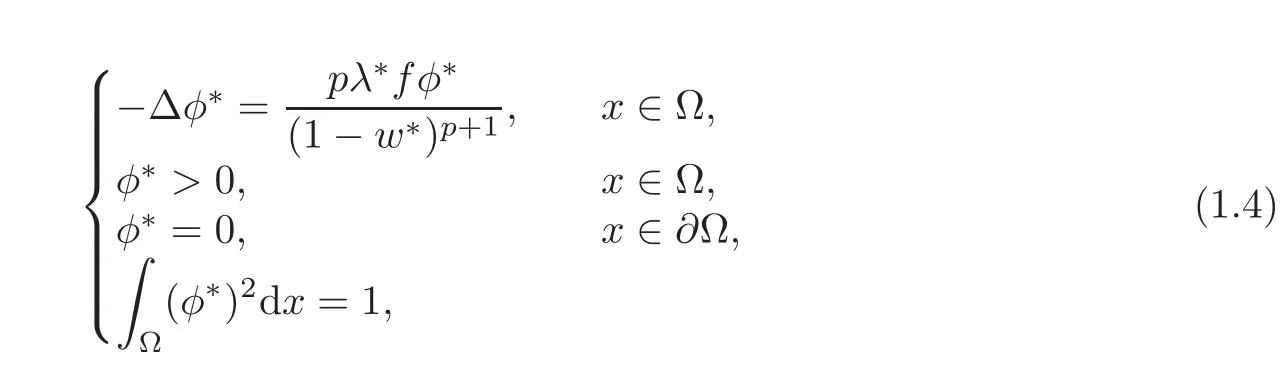
and there is an estimate for the quenching time T∗if u0(x)=0,that is

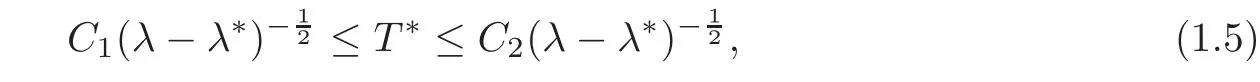
as λ ＞ λ∗and close to λ∗,where C1and C2are independent of λ.This tells us that

Our purpose is to deal with the problem(1.1),and this paper will be organized as follows.In Section 2,motivated by the bounds(1.5)on the quenching time T∗,we find an asymptotic approximation for T∗in the limiting case when w∗is regular,u0(x)=0,λ ＞ λ∗and λ → λ∗.In Section 3,we consider what conditions λ and initial data u0(x)satisfy can lead to the quenching of u.In Section 4,wefind conditions on the initial data u0which are sufficient to lead to the nonexistence of u after a finite time,for λ ＜ λ∗.The case of that w∗is singular is considered in Section 5.In Section 6,we discuss the global existence of the solution to(1.1).In Section 7,we will give some comments of our results.

2 Asymptotic Estimate for T∗for Small λ−λ∗＞ 0 if w∗is Regular

In this section,assume that u0=0,and w∗is a regular solution to(1.2)with λ = λ∗.Motivated by(1.5),we shall consider the limit of λ − λ∗→ 0+to estimate the quenching time T∗,as an asymptotic expression for λ − λ∗≪ 1.We shall adapt and improve some of the arguments in[15]to get the following theorem.

ProofFirst recall from[22]that since Ω =BR(0),f(x)=f(|x|),f′≤ 0,we have that the quenching set is just{0}.

Let u∗(x,t)be a solution to(1.1)with λ = λ∗.Since u0=0,by the standard parabolic comparison principle,we have u∗(x,t)≤ w∗(x).Since w∗(x)is a solution to(1.2)with λ = λ∗,then u∗(x,t)converges to a regular solution to(1.2)with λ = λ∗.By the uniqueness of solution to(1.2),we get thatu∗(x,t)=w∗(x).

By(1.1)–(1.2),we obtain that u∗(x,t)and w∗(x)satisfy

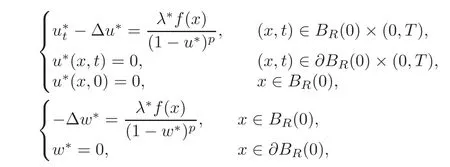
respectively.Hence similarly to(43)in[15],we canfind that

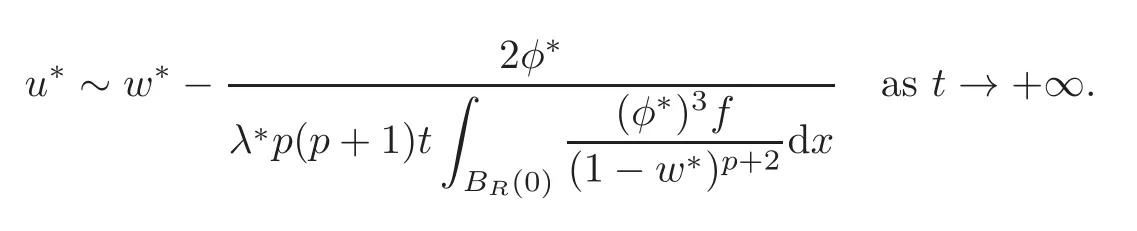
Now denote λ − λ∗by η.We first use the formal Taylor expansion on u,which means

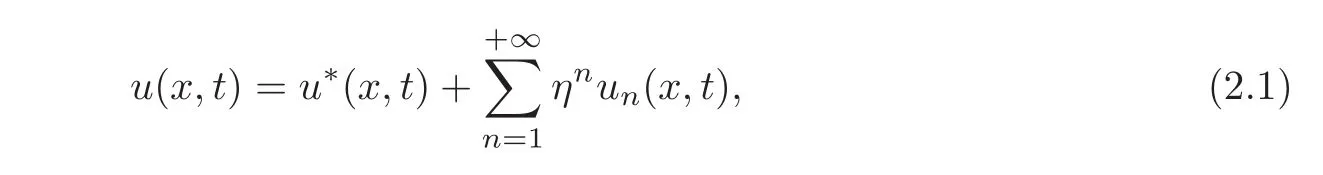
where u∗is a solution to(1.1)with λ = λ∗.According to the equation with u∗and u,we get that

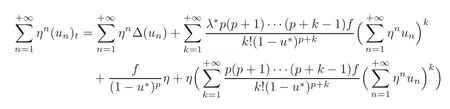
and

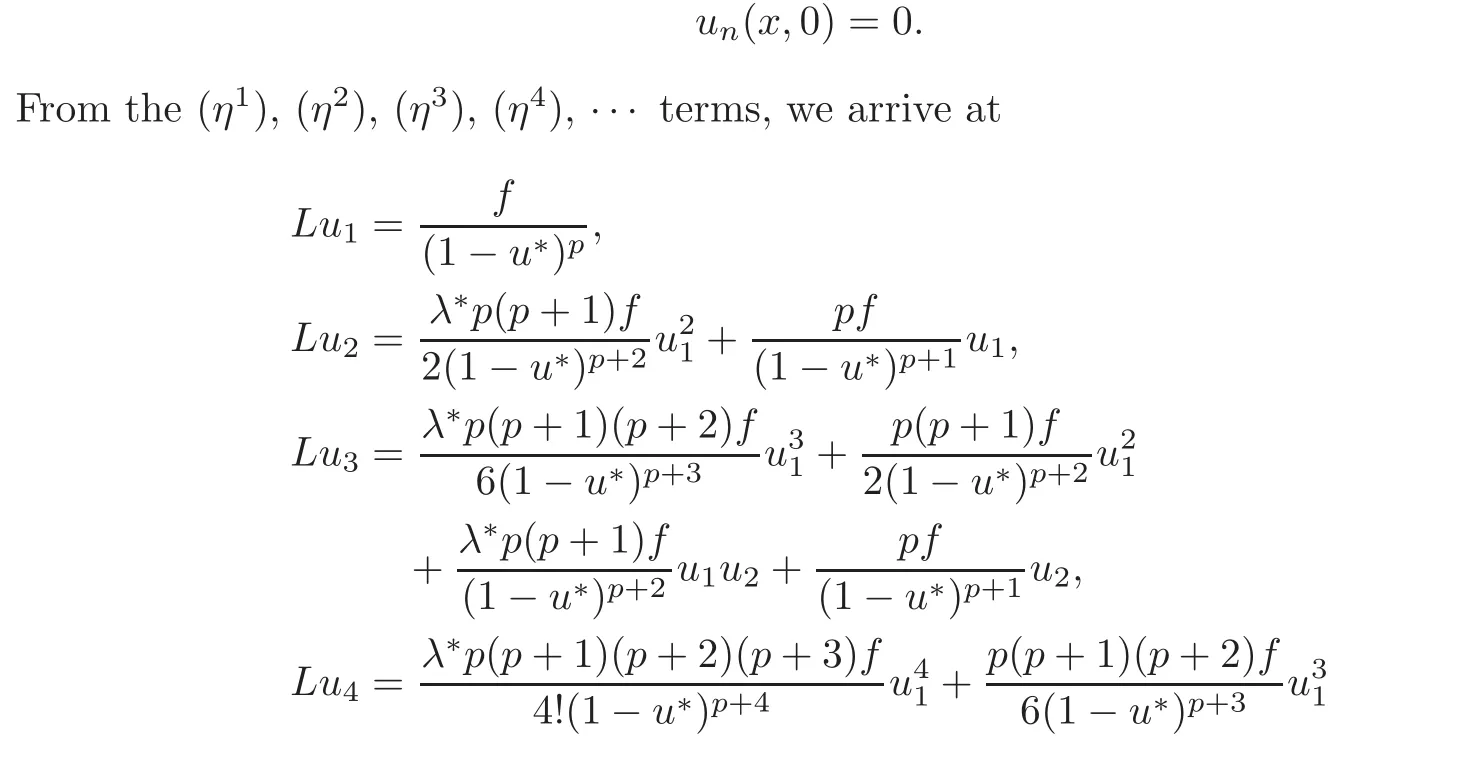
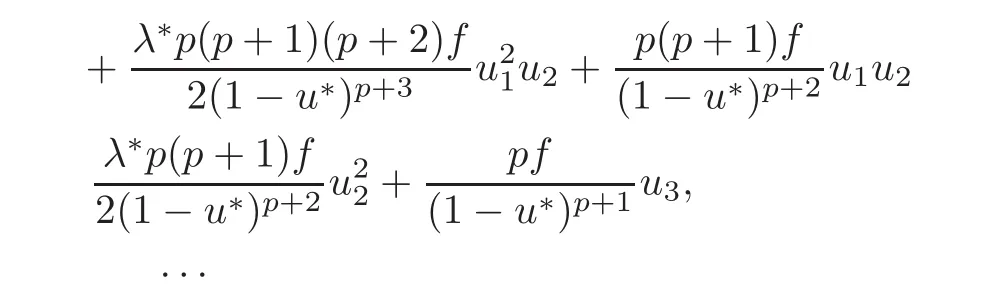
where the operator L is defined asBy the standard parabolic regularity theory(see[14]),as‖u∗‖∞≤ ‖w∗‖∞,we obtain that for any T0＜ T∗,

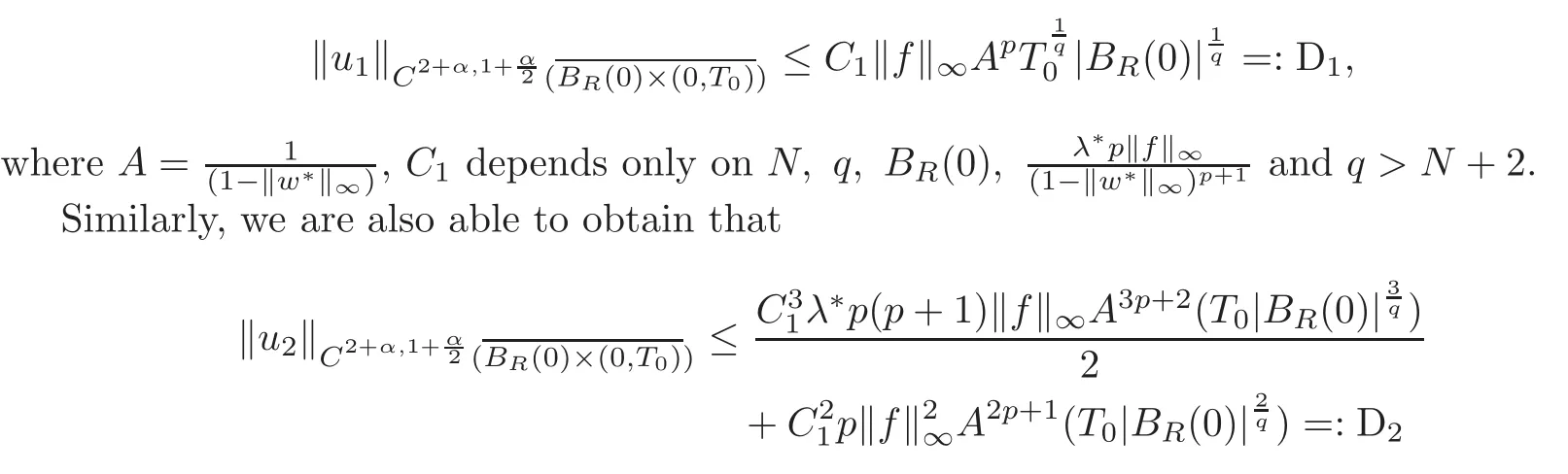
and

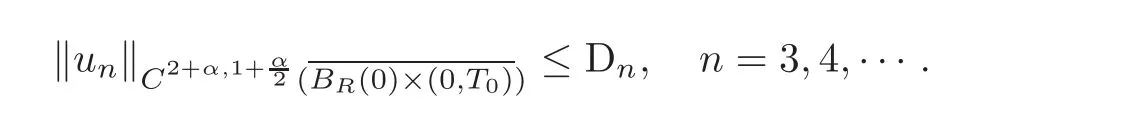
In fact by iteration we can get that the highest exponent of A in Dnis p+2(n−1)(p+1),the highest exponent of p in Dnis 2n,the highest exponent of(T0|BR(0)|)in Dnis 2n−1,the highest exponent of C1in Dnis 2n−1,the highest exponent of‖f‖∞in Dnis 2n−1.

So we can obtain that

which means the convergence domain of series(2.1)has a positive measure.Therefore,series(2.1)is convergent uniformly,provided that η is small enough.For the same reason,we get

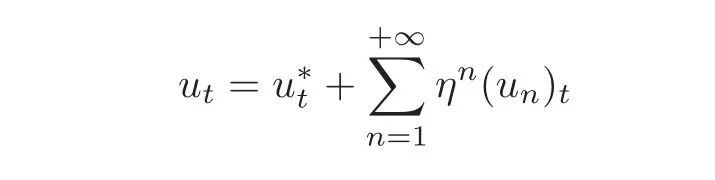
and

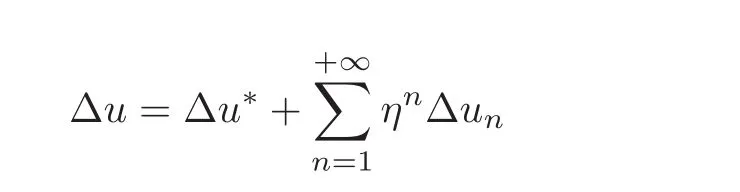
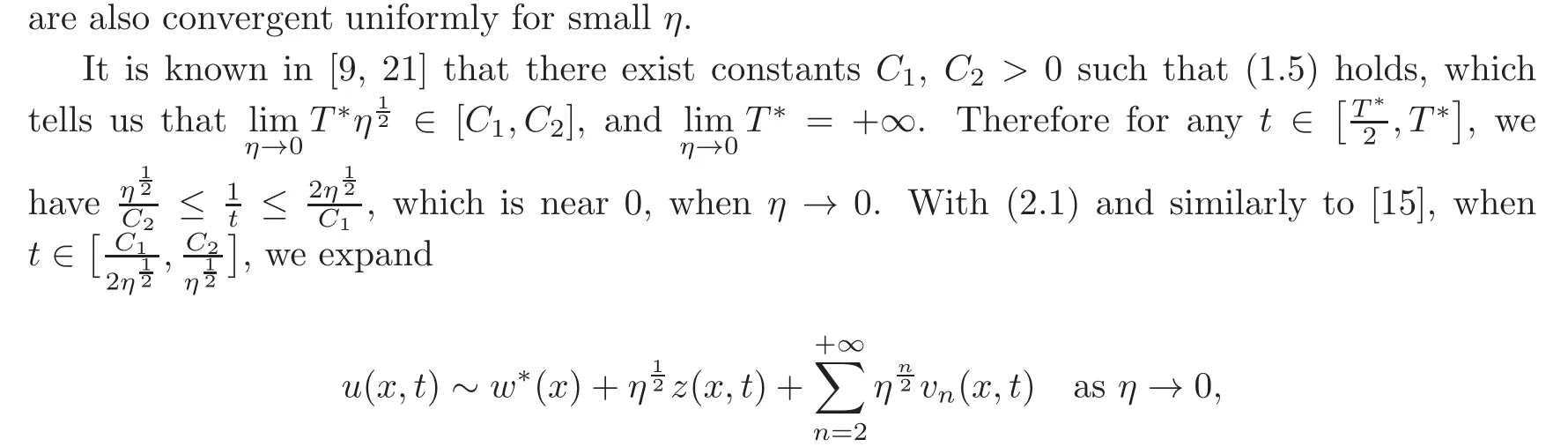
where z(x,t)is to be determined.On making a change in timescale t=the equation(1.1)gives

where we have used Taylor expansion.

From the(η12)terms in(2.2),we have

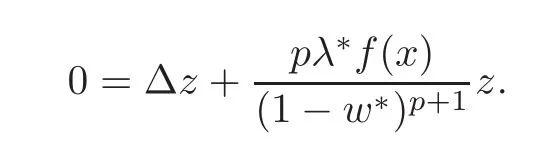
Since the problem above has the form of problem(1.4),for some continuous function a1(τ),we can write

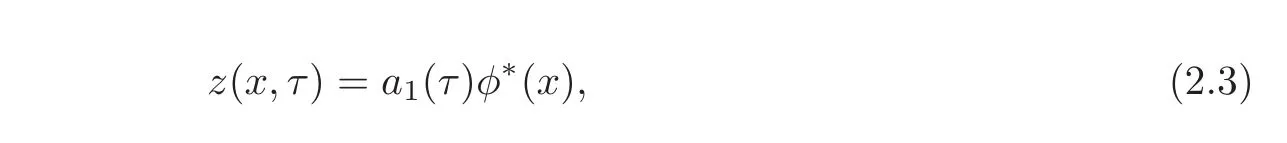
where φ∗satisfies the condition of this theorem.

From the(η1)terms in(2.2),by(2.3)we arrive at

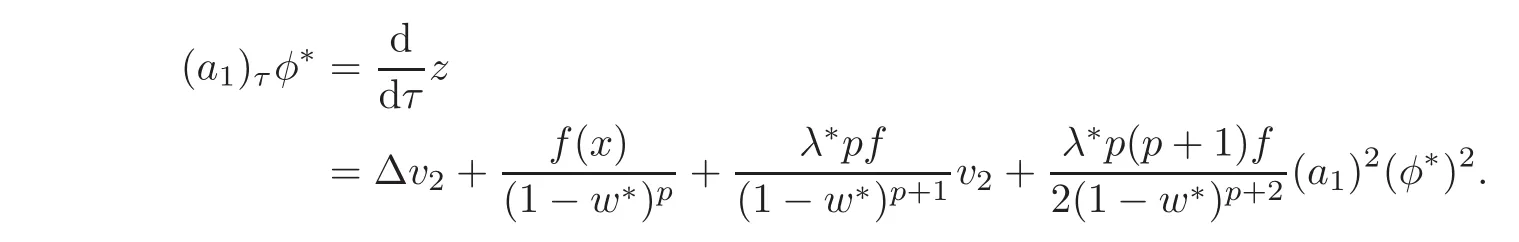
By multiplying φ∗on both side and integrating over BR(0),we get

3 Quenching Phenomenon of u for General λ and Initial Data u0(x)

In this section,we do not need to assume u0(x)≡0 any more.We are going to consider for which λ and u0(x)the solution to(1.1)will hit 1.We have the following theorem.

Theorem 3.1Ifλand initial datau0(x)satisfy

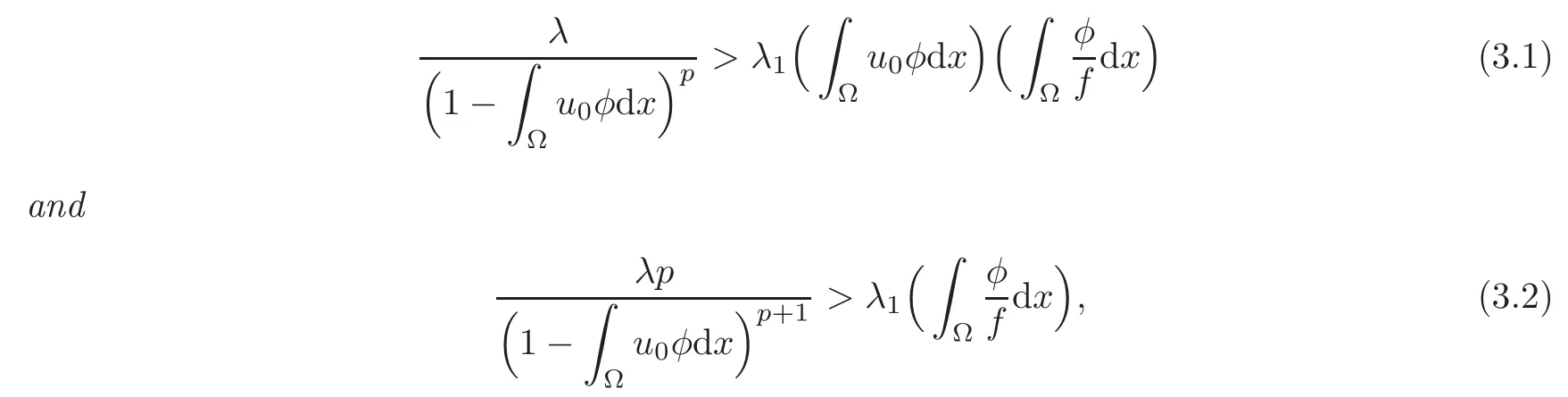
It is clear that G(t)is well defined on the existence interval of the solution u.

Differentiating G(t)yields that

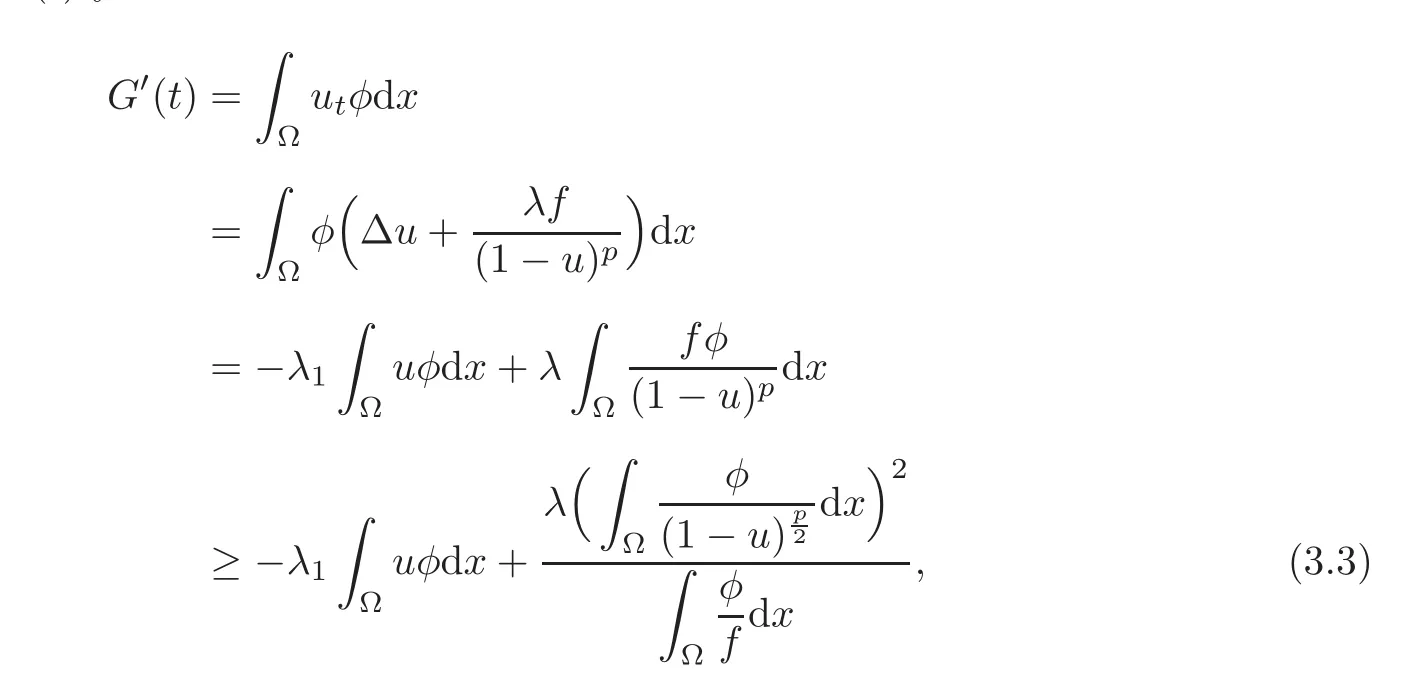
where Hö lder inequality is used in the last inequality.By Jensen’s inequality,if p ＞ 1,

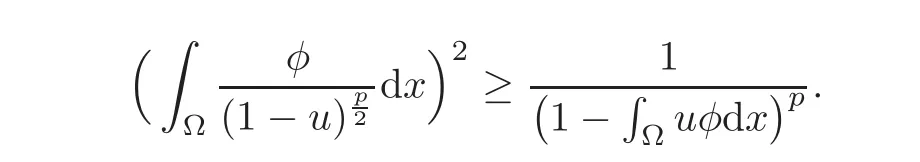
Substituting it into(3.3),we obtain

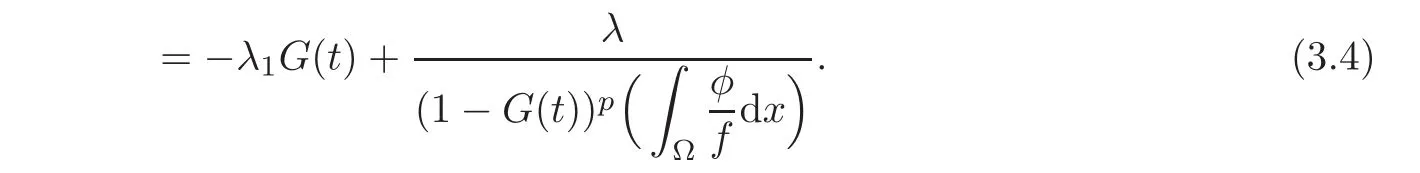
If u remains smaller than 1 for all t,then G(t)is defined and smaller than 1 for all t.However,from the ODE theory,G(t)will blow up(reach 1)at a finite time,provided that λ and the initial data u0satisfy(3.1)and(3.2),because−λ1G(t)+is increasing with respect to G(t)and G′(0)≥ −λ1G(0)+under the conditions(3.1)and(3.2).Then the proof of this theorem is complete.

4 Quenching Phenomenon of u for General 0＜λ＜λ∗

In this section,we are going to check when the solution u to(1.1)will quench even for λ ＜ λ∗.We will compare u0with some suitable function.

4.1 (1.2)has a second nonminimal solution w＞0

If w is a nonminimal solution to(1.2),from[10],we deduce that the principal eigenvalueµ1,λ(w)associated with the eigenfunction φ1,for the problem

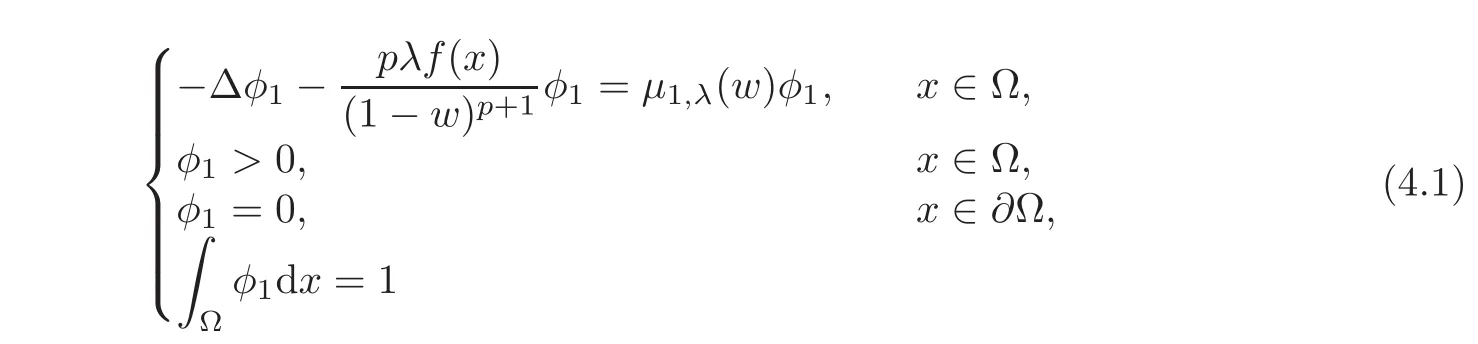
is negative.Then we have the following theorem.

Theorem 4.1Assume that(1.2)has a nonminimal solutionwforλ ＜ λ∗,and assume‖w‖∞＜ 1.Then forλ ＜ λ∗,the solutionuto(1.1)will quench at afinite timeT∗,provided thatu0(x)≥ w(x)andu0(x)/≡ w(x).

ProofSetting v(x,t)=u(x,t)−w(x),we have

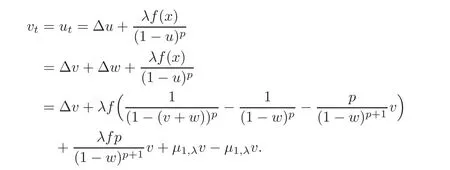
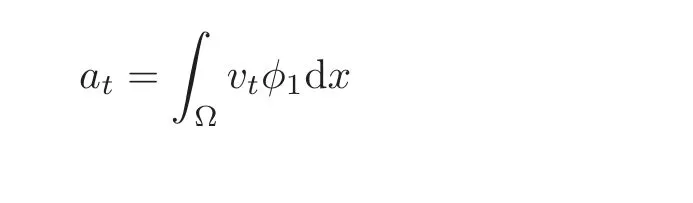
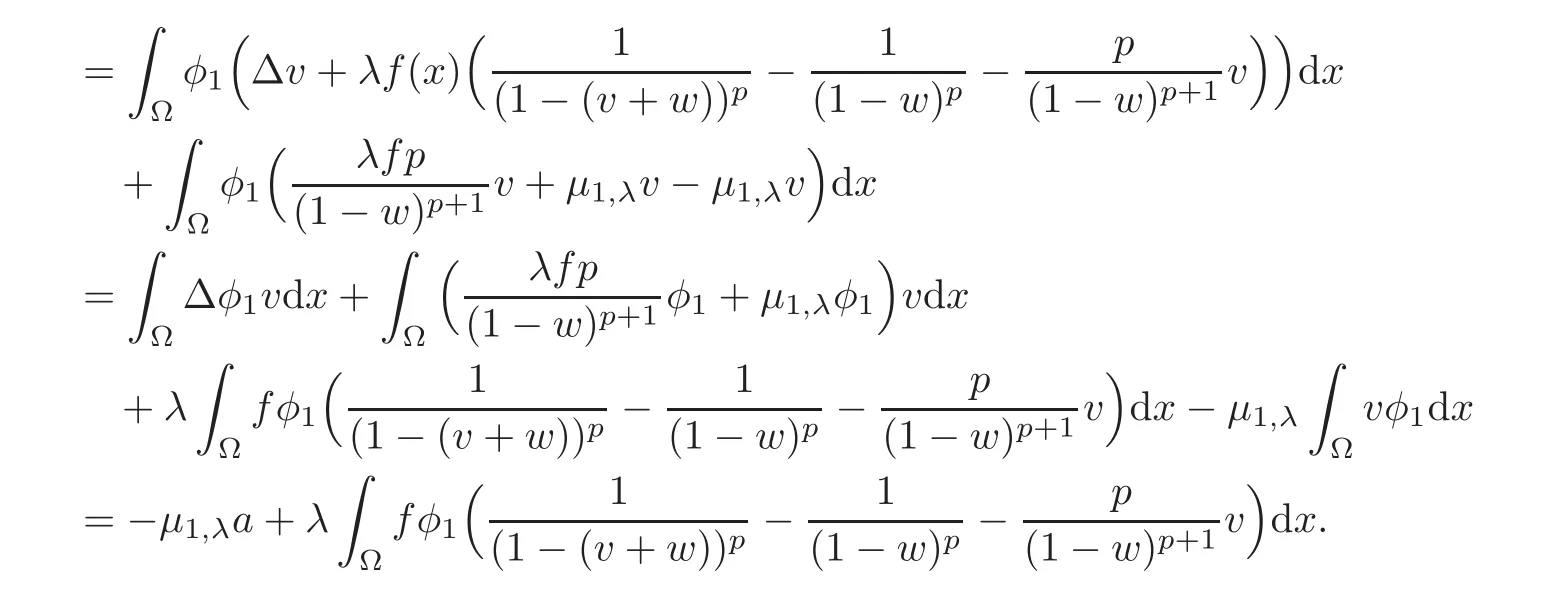
The inequalities

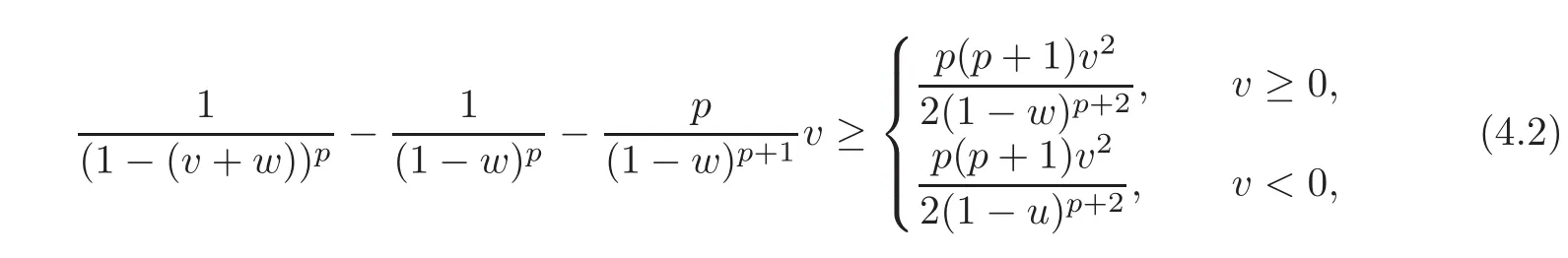
and Hö lder inequality yield that

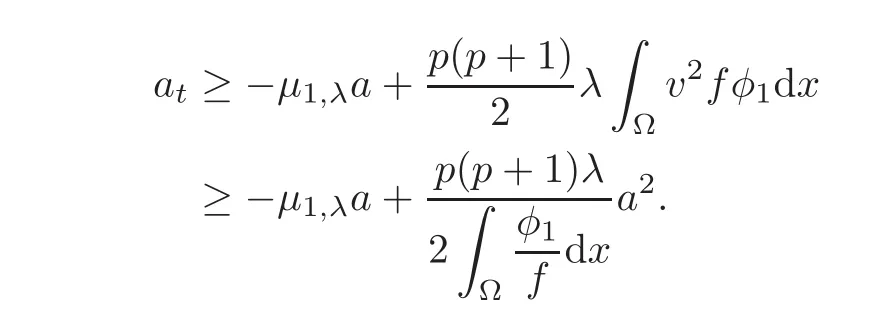
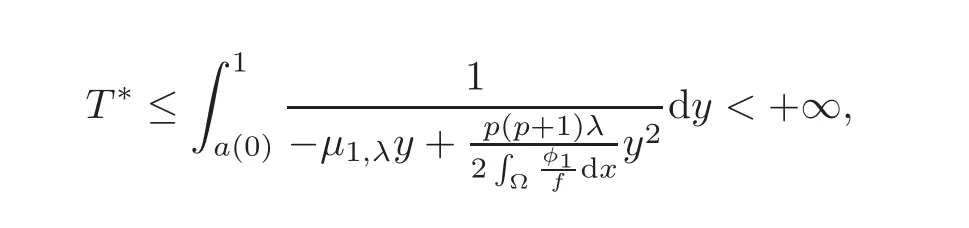
and the proof is complete.

Remark 4.1It can be deduced from[6]that when λ → (λ∗)−,there exists a nonminimal solution w to(1.2);and ifµk,λ(w) ≥ 0,then ‖w‖∞＜ 1,where µk,λ(w)is the k-th eigenvalue of problem(1.4),k≥2.

This remark says that the assumption in Theorem 4.1 is reasonable,provided that λ → (λ∗)−and there exists a k ≥ 2 such thatµk,λ(w)≥ 0.

4.2 (1.2)may admit a unique solution w for λ ∈ (0,λ∗)small enough

In[5,10],we know that when λ is small enough,(1.2)has only a unique minimal solution.Therefore,we need to choose another suitable function to compare with the initial data u0(x).In this part,let Ω =B1(0),f(x)≡ 1.And we need assume N=3,p=2 for simplicity.For general N,p,the idea is similar.Now we establish the theorem below.

Theorem 4.2LetN=3,p=2,f(x)≡1,Ω=B1(0).Then the solutionuto(1.1)willquench at afinite timeT∗,ifu0(x)≥ z(x)andu0(x)/≡ z(x),where

and

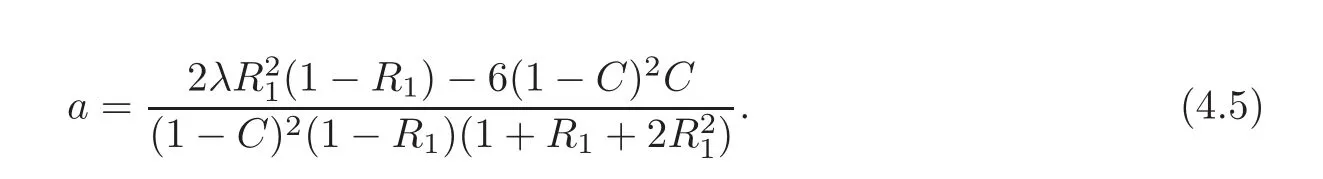
ProofLet z(x)satisfy(4.3)–(4.5).Then we have

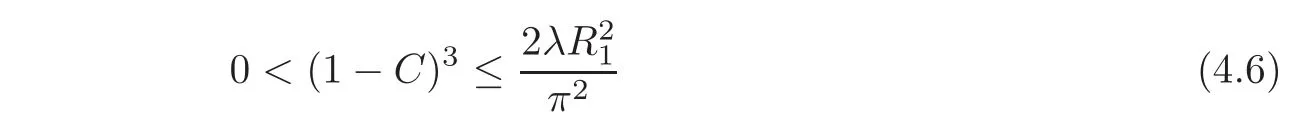
and z ∈ C1,α(B1(0)).

Consider now the following eigenvalue problem:

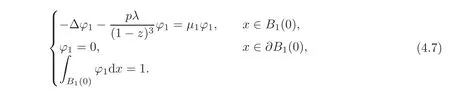
From(4.6)we reach thatµ1＜ 0.Moreover‖z‖L∞(B1(0))=z(0)＜ 1,a≤ λ.

Next,we set v(x,t)=u(x,t)−z(x),then v(x,0)=u0(x)−z(x)in B1(0).Let a2(t)=

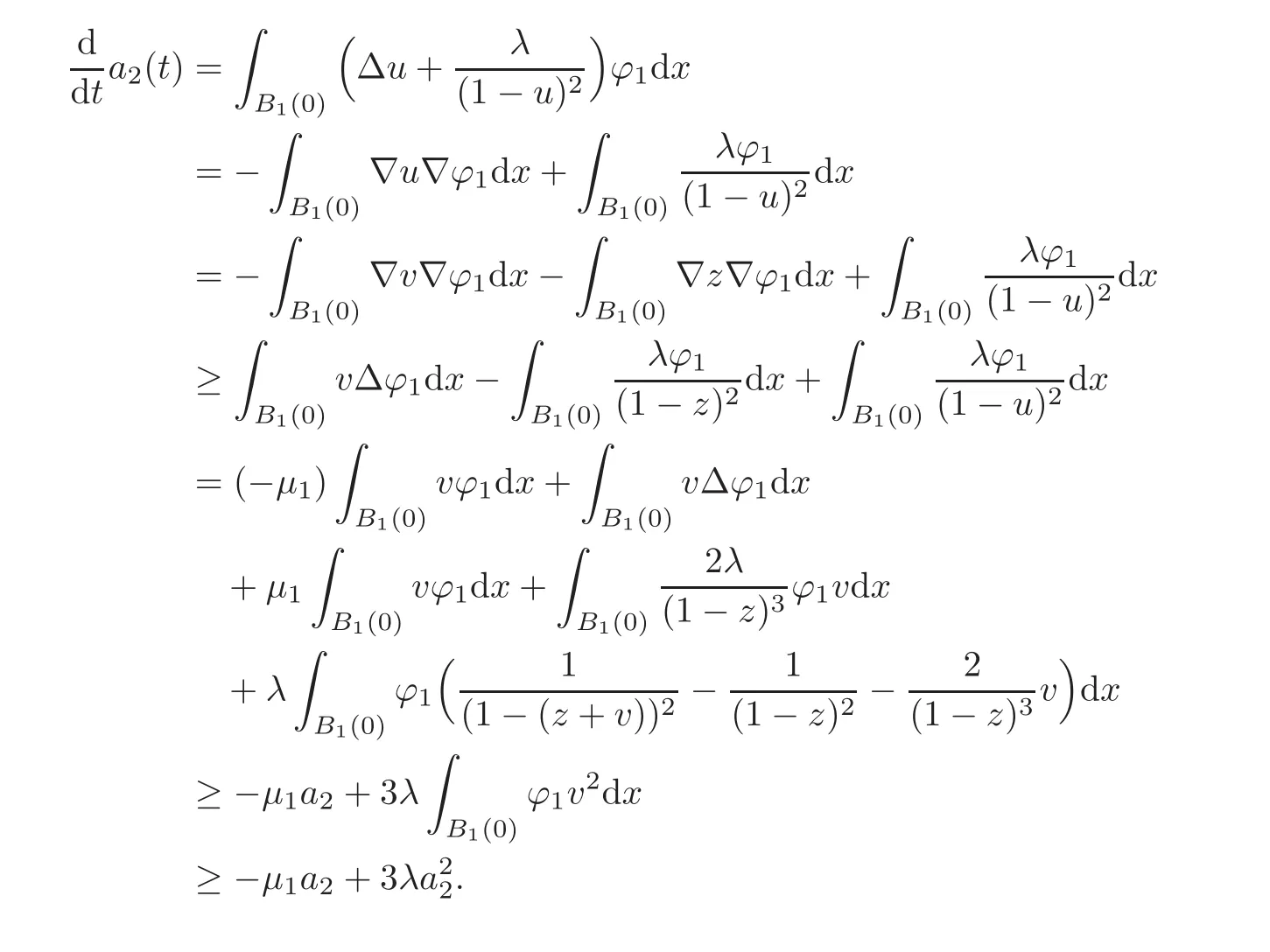
The last inequality is due to Hö lder inequality.As

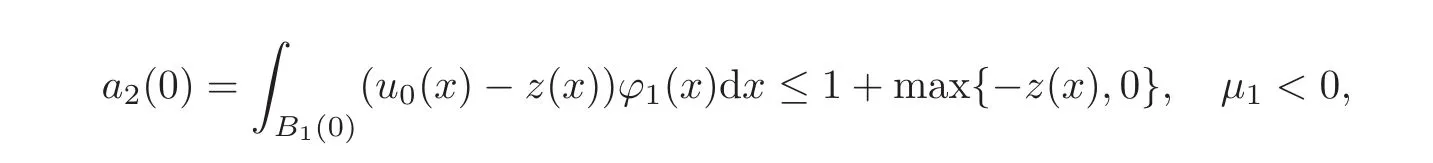
we conclude that if u0(x)≥ z(x)and u0(x)/≡ z(x),the quenching time T∗for the solution u verifies

where z(x)is as stated in(4.3).Thisfinishes the proof of the theorem.

5 Quenching Phenomenon of u for λ ＞ λ∗,if w∗ is Singular

Now we discuss the case where w∗is singular.For any minimal stable solution wΛto(1.2)with λ being replaced by Λ,0 ≤ Λ ＜ λ∗,we consider the problem

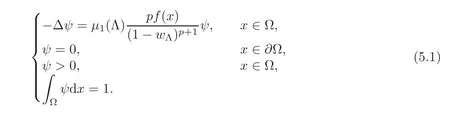
which is impossible,because wΛis stable.Hence our claim is concluded.

Take λ1∈ (µ0,µ1(0)),then there exists a unique λ2∈ (0,λ∗),such that µ1(λ2)= λ1,and λ2＜ λ∗≤ µ0＜ λ1.Now we give our theorem.

for anyλ ＞ λ∗,and

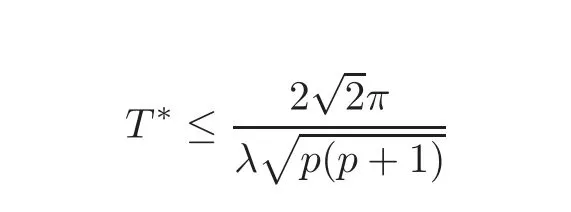
forλlarger than and close toλ∗.

ProofLet w be the minimal solution to

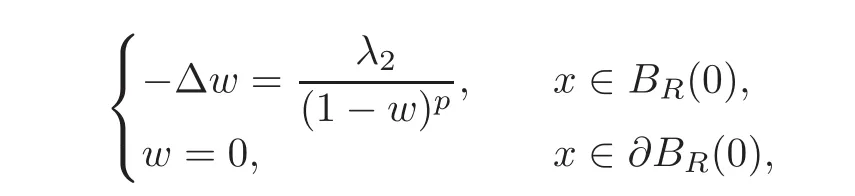
where µ1(0)＞ µ0≥ λ∗＞ λ2.Let v(x,t)=u(x,t)−w(x)and∈ [µ0,µ1(0)],then λ2＜and for any λ ＞we have

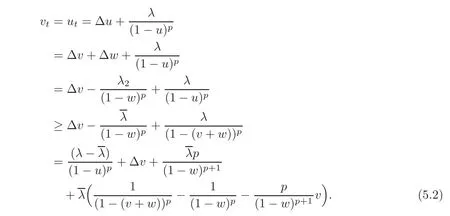
Multiplying(5.2)by ψ,where ψ satisfies(5.1)withand integrating over BR(0)yield that

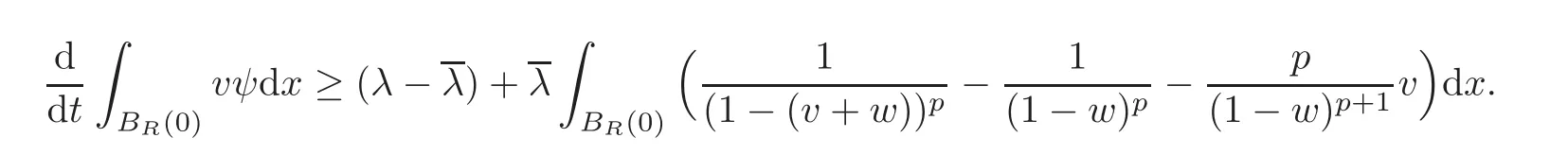
Hö lder inequality and(4.2)enable us that

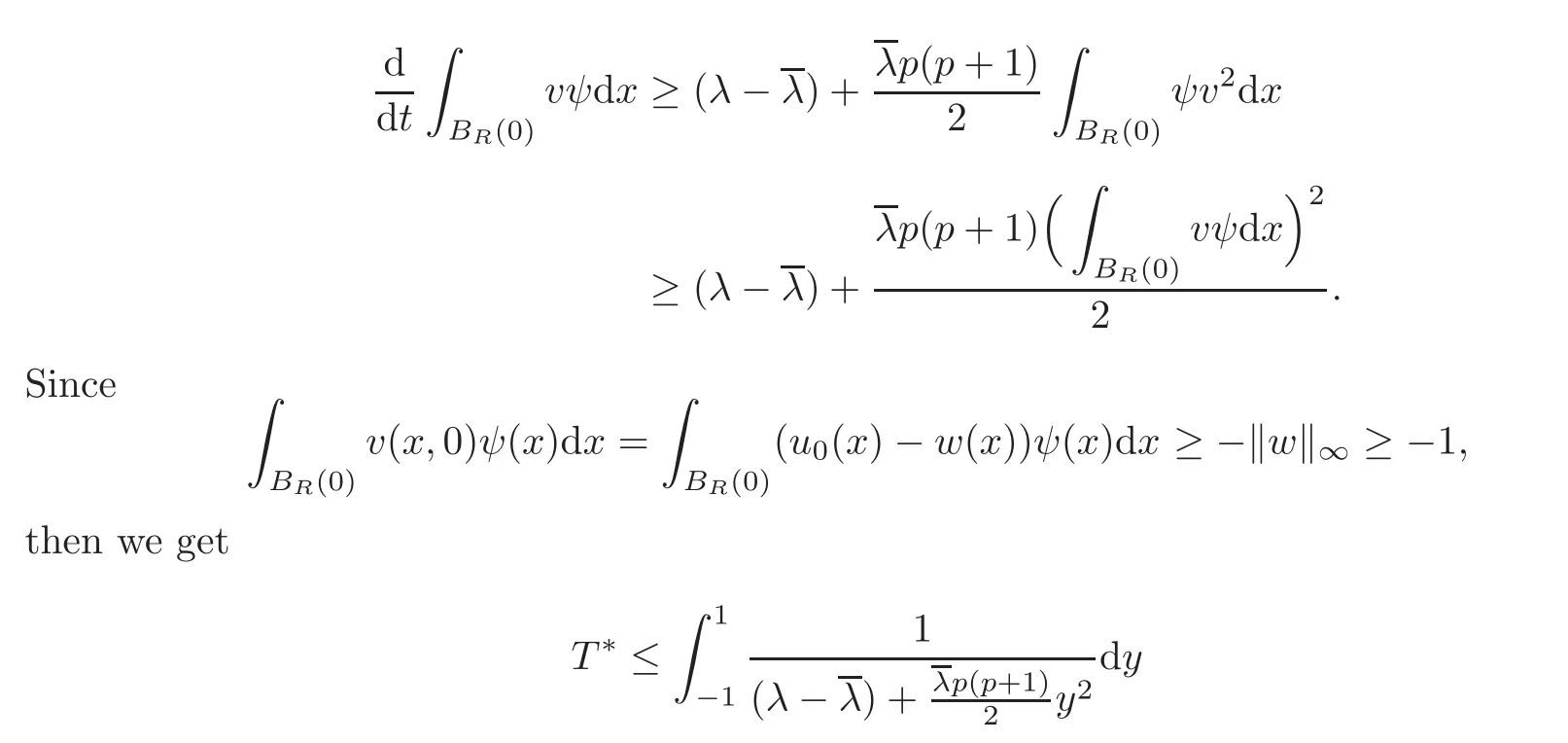
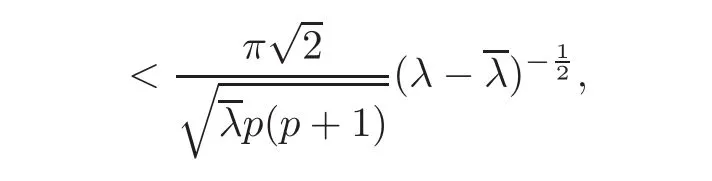
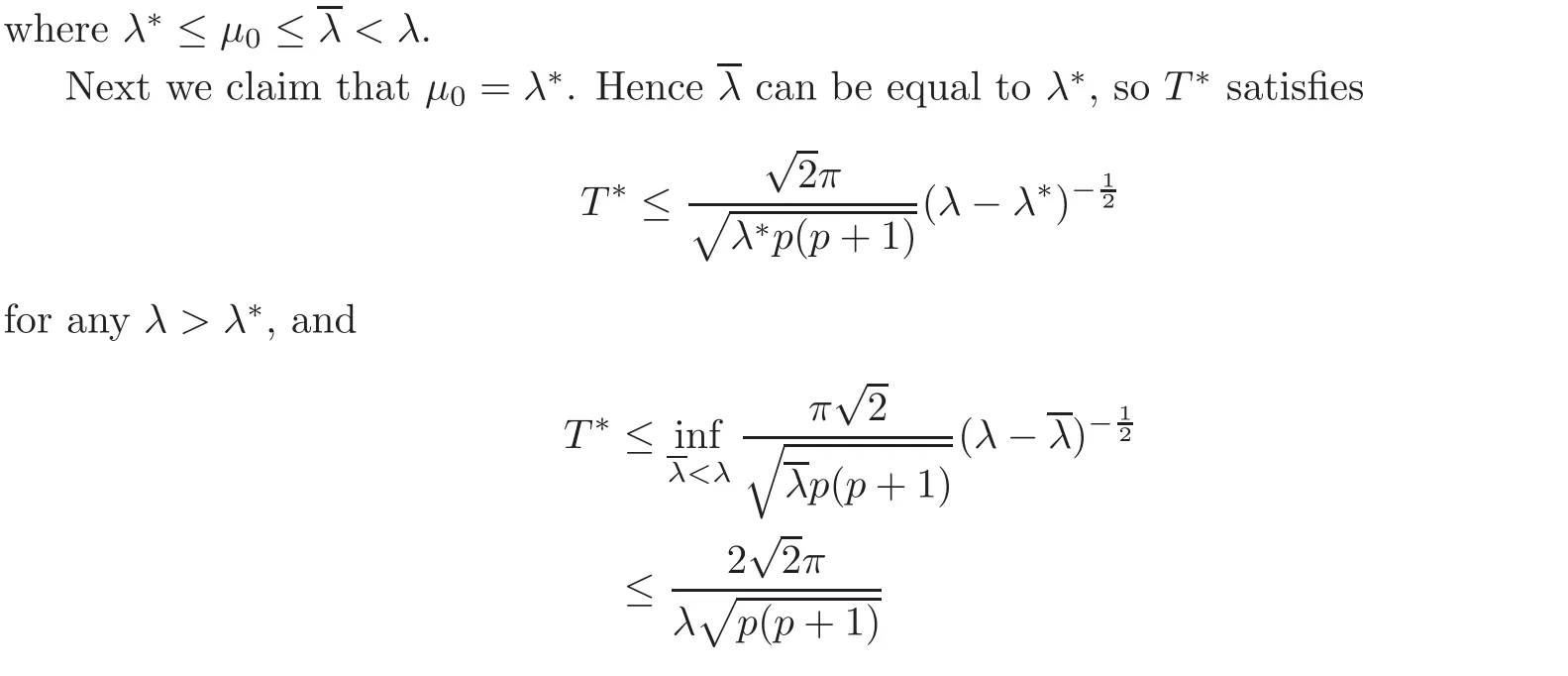
for λ larger than and close to λ∗.

Thereforeµ0= λ∗.Hence our claim is correct and the theorem is proved.

6 Global Existence for the Solution to(1.1)

In this section,we will check the global existence of the solution.In fact,under some circumstances the solution of(1.1)should exist globally.That means that we have the following theorem.

Theorem 6.1Suppose thatΩ =BR(0)andf(x)≡ fis a constant.Assume that the initial datumu0is a subsolution to(1.2),and let

Then if u0(x)≤z(x),applying the maximum principle,we reach that u(x)≤z(x)＜1,which means that u(x)exists globally.This completes the proof of this theorem.

7 Discussion of Results

We have found in Sections 2–5 the circumstances under which the solution to problem(1.1)exhibits the phenomenon of quenching.

In order to apply these results,we first need to decide the value of λ∗.Although there is not exact expression of λ∗,some people have given some estimates of λ∗.For example,from[22]we can easily deduce that

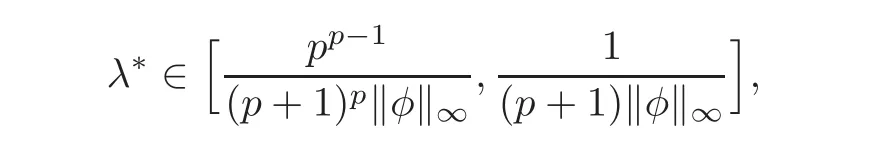
the extremal solution w∗to(1.2)is regular.

Hence,if w∗is regular,we apply the results of Section 2 to give

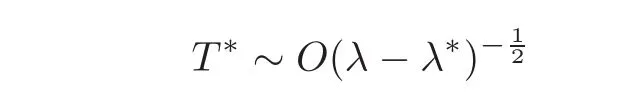
as λ → (λ∗)+.For general λ and initial data u0(x),Section 3 tells us the condition under which the solution u to(1.1)will quench.For λ ＜ λ∗,we consider two situations:(1.2)has a nonminimal solution;(1.2)may only admit a unique minimal solution.In both situations,we need u0(x)satisfy suitable condition,then in Section 4 we obtain T∗＜+∞.The rationa lity of these two situations is as follows:From[6],it follows that whenthere exists δ＞ 0 such that for any λ ∈ (λ∗− δ,λ∗),problem(1.2)has a nonminimal second solution w ≥ wλ.Meanwhile,it is well known that if Ω ⊂ RN(N ≥ 3)is star-shaped,or Ω is strictly convex in R2,then(1.2)admits a unique solution for λ＞0 small enough(see[5]).

If w∗is singular,in Section 5,we show that the quenching time T∗＜ +∞,for λ ＞ λ∗.

In Section 6,we make a short discussion about the situation of the global existence for the solution to(1.1).We can get that if the initial data is suitable small,then for λ ＜ λ∗,the quenching phenomenon will not occur.

[1]Ambrosetti,A.and Prodi,G.,A Primer of Nonlinear Analysis,Cambridge University Press,Cambridge,Massachusetts,1995.

[2]Brauner,C.M.and Nicolaenko,B.,Sur une classe de problemes elliptiques non lineaires,C.R.Acad.Sci.Paris A,286,1978,1007–1010.

[3]Brezis,H.,Cazenave,T.,Martel,Y.and Ramiandrisoa,A.,Blow-up for ut−∆u=g(u)revisited,Advances in Differential Equations,1,1996,73–90.

[4]Cantrell,R.S.and Cosner,C.,Spatial Ecology via Reaction-Diffusion Equations,Wiley,Chichester,2003.

[5]Esposito,P.and Ghoussoub,N.,Uniqueness of solutions for an elliptic equation modeling MEMS,Methods Appl.Anal.,15(3),2008,341–354.

[6]Esposito,P.,Ghoussoub,N.and Guo,Y.J.,Compactness along the branch of semistable and unstable solutions for an elliptic problem with a singular nonlinearity,Comm.Pure Appl.Math.,60(12),2007,1731–1768.

[7]Esposito,P.,Ghoussoub,N.and Guo,Y.J.,Mathematical analysis of partial differential equations modeling electrostatic MEMS,Courant Lecture Notes in Mathematics,20,Courant Institute of Mathematical Sciences,New York;American Mathematical Society,Providence,RI,2010.

[8]Flores,G.,Mercado,G.A.and Pelesko,J.A.,Dynamics and touchdown in electrostatic MEMS,Proceedings of ASME DETC’03,IEEE Computer Soc.,2003,1–8.

[9]Ghoussoub,N.and Guo,Y.J.,Estimates for the quenching time of a parabolic equation modeling electrostatic MEMS,Methods Appl.Anal.,15(3),2008,361–376.

[10]Ghoussoub,N.and Guo,Y.J.,On the partial differential equations of electrostatic MEMS devices:Stationary case,SIAM J.Math.Anal.,38,2007,1423–1449.

[11]Ghoussoub,N.and Guo,Y.J.,On the partial differential equations of electrostatic MEMS devices II:Dynamic case,NoDEA Nonlinear Differ.Equ.Appl.,15,2008,115–145.

[12]Ghoussoub,N.and Guo,Y.J.,On the partial differential equations of electrostatic MEMS devices III:Refined touchdown behavior,J.Differ.Equ.,244,2008,2277–2309.

[13]Guo,Y.J.,Pan,Z.G.and Ward,M.J.,Touchdown and pull-in voltage behavior of an MEMS device with varying dielectric properties,SIAM J.Appl.Math.,66(1),2005,309–338.

[14]Hu,B.,Blow-up Theories for Semilinear Parabolic Equations,Springer-Verlag,Berlin,2011.

[15]Lacey,A.A.,Mathematical analysis of thermal runaway for spatially inhomogeneous reactions,SIAM J.Appl.Math.,43,1983,1350–1366.

[16]Lin,F.H.and Yang,Y.S.,Nonlinear non-local elliptic equation modelling electrostatic actuation,Proc.R.Soc.A,463,2007,1323–1337.

[17]Mignot,F.and Puel,J.P.,Sur une classe de probleme non lineaires avec non linearite positive,croissante,convexe,Comm.P.D.E.,5(8),1980,791–836.

[18]Pelesko,J.A.and Berstein,D.H.,Modeling MEMS and NEMS,Chapman&Hall/CRC,Boca Raton,2002.

[19]Pelesko,J.A.,Mathematical modeling of electrostatic MEMS with tailored dielectric properties,SIAM J.Appl.Math.,62(3),2002,888–908.

[20]Sattinger,D.H.,Monotone methods in nonlinear elliptic and parabolic boundary value problems,Indiana Univ.Math.J.,21,1972,979–1000.

[21]Wang,Q.,Estimates for the quenching time of an MEMS equation with fringingfield,J.Math.Anal.Appl.,405,2013,135–147.

[22]Ye,D.and Zhou,F.,On a general family of nonautonomous elliptic and parabolic equations,Calc.Var.,37,2010,259–274.