Nongeneric Bifurcations Near a Nontransversal Heterodimensional Cycle∗

Xingbo LIU Xiaofei WANG Ting WANG

1 Introduction and Hypotheses

In recent years,bifurcation theory has attracted lots of attention due to its important role in applications(see[1–3]).Especially,different kinds of high co-dimensional homoclinic or heteroclinic bifurcations have been studied in detail.[4]studied the inclination-flip homoclinic orbit together with two other codimension 2 homoclinic bifurcations,which are cases of resonant bifurcation and orbit-flip bifurcation.[5]investigated codimension-two bifurcations of homoclinic orbits with an orbit flip.For other references,see[6–8]and the references cited therein.

[9]considered the bifurcation of heterodimensional cycles in dynamical systems.A heteroclinic cycle is said to be equidimensional if all the equilibrium points in the cycle have the same index(dimension of the stable manifold).Otherwise,such a cycle is called heterodimensional.Heterodimensional cycles,as a special kind of heteroclinic cycle,were found in many practical problems(see[10–11]).Bykov made an essential contribution to the topic of the paper under consideration(see[12],where the unfolding of codim-0/codim-2 cycles was studied).[13]analyzed homoclinic orbits near heterodimensional cycles between an equilibrium and a periodic orbit in three dimensions.For other references about heterodimensional cycles,see[14–19]and the references cited therein.

Usually,a generic heterodimensional cycle is composed by a codim-0/codim-2 heteroclinic orbit between two real saddle equilibrium.However a heterodimensional cycle may exhibit different degeneracies for some reasons(see[18–20]).The study in[20]revealed another degeneracy that the two heteroclinic orbits of the heterodimensional cycle are both nontransversal,that was found in Chua’s equation.Notice that there are few papers on nontransversal heterodimensional cycle problems concerning orbitflips.Motivated by this fact,in this paper,we confine ourselves to study the bifurcation of the nongeneric heterodimensional cycle with orbitflip if the nontransversal intersection of the two-dimensional manifolds occurs at the same time.

We will present the bifurcation results on different parameter regions,and we will show that under the stronger degeneracy conditions-nontransversality and orbitflip,the problem under consideration in our paper has the richer dynamics than the problem discussed in the literature[17],where they discussed the nontransversal heterodimensional cycle with no orbitflip.For example,the heterodimensional cycle can coexist with periodic orbit,but this can not happen in the case in[17].In addition,we also give an example to demonstrate the existence of the system which has a nontransversal heterodimensional with one orbitflip.

The difficulty for us is how to show the different degeneracy(including the nontransversality and the orbitflip)in the return map.The technique we have used here is the Shilnikov coordinates and the local moving frame,the latter is introduced in[21],and then improved in[22–23]etc.By establishing the local coordinates and Poincar´e maps in a sufficiently small neighborhood of the primary cycle,we theoretically show that the different bifurcation surfaces exhibits variety and complexity of the bifurcations of degenerate heterodimensional cycles.

Consider the following Crsystem:

and its unperturbed system

where r≥ 4,z∈R3,µ ∈ Rl,l≥ 3,0≤ |µ|≪ 1,g(z,0)=0,f(z)is Crwith respect to the phase variable z,g(z,µ)is Crwith respect to the phase variable z and the parameter µ.We also assume that:

(H1)System(1.2)has two hyperbolic equilibria pi,i=1,2.are the Crstable and unstable manifolds of pi,respectively.In addition,the linearization matrix Df(p1)has three simple real eigenvalues:satisfying

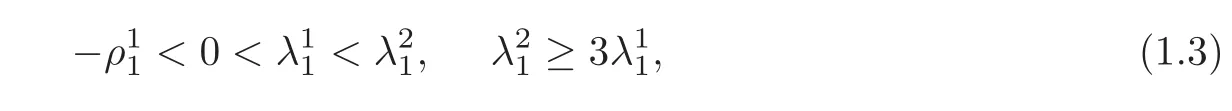
and Df(p2)has three simple real eigenvalues:satisfying

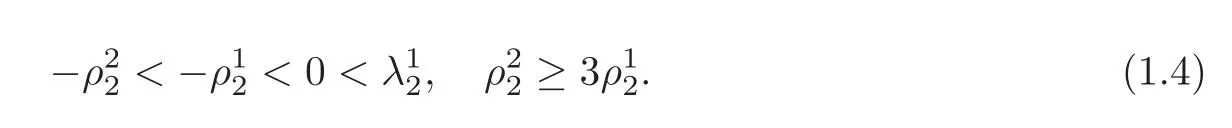
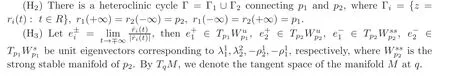
Figure 1 Heterodimensional cycle Γ = Γ1∪ Γ2.

(H4)(Nontransversal condition)There is a nontransversal intersection between the twodimensional manifolds of pialong the heteroclinic orbit Γ1,that is,is coincident withalong Γ1.

As we will see,the bifurcations under consideration heavily depend on the relations between the eigenvalues of pi,i=1,2.Without loss of generality,we may assume

(H5)

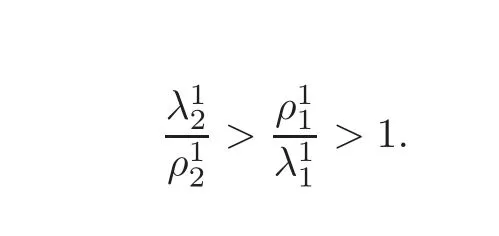
The rest of the paper is organized as follows.In Section 2,the Poincar´e map and the successor function are obtained by the establishment of a local moving frame system near the unperturbed heterodimensional cycle.Then,bifurcation equations are derived by using the implicit function theorem.Section 3 presents the bifurcation results on different parameter regions and the sufficient conditions for the persistence of heterodimensional cycle,the existence of homoclinic orbit and periodic orbit,the noncoexistence and coexistence of heterodimensional cycle,periodic orbit and homoclinic orbit.An analytical example is demonstrated to illustrate our main results in the last section.

2 Local Coordinates and Poincar´e Maps

Following[25],as a direct application of the stable(unstable)manifold theorem and the strong stable(unstable)manifold theorem,we take two successive Crand Cr−1transformations to straighten the local stable manifold,unstable manifold,strong unstable manifold in the region of Uisuch that the system(1.1)has the following form in the small neighborhood U1of p1:

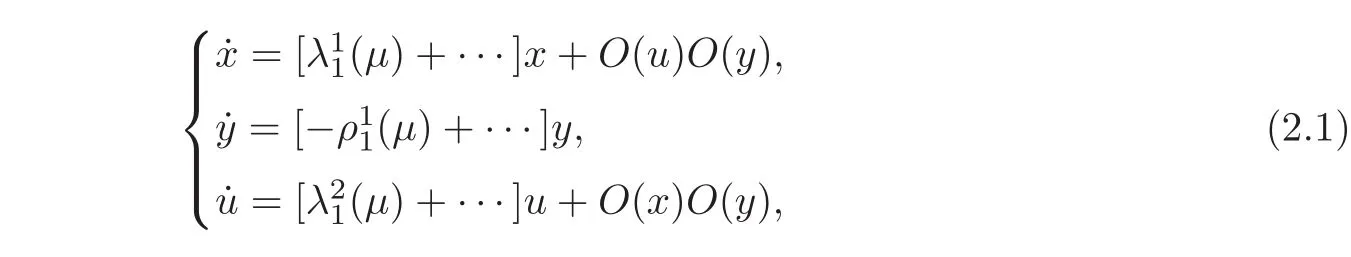
and has the following form in the neighborhood U2of p2:

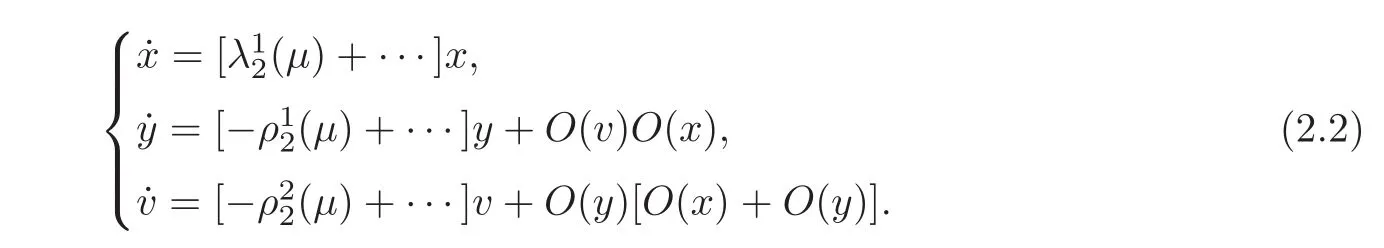
Note that these two systems are adjoint in the sense that if Z(t)is the solution matrix of(2.3),then(Z−1(t))∗is the solution matrix of(2.4).

In the following,we will choose suitable solutions of the corresponding linear variational equation as a local coordinate system along Γi.

Following the idea in[17],we know that there exists a fundamental solution matrix Z1(t)=for the system(2.3)satisfying

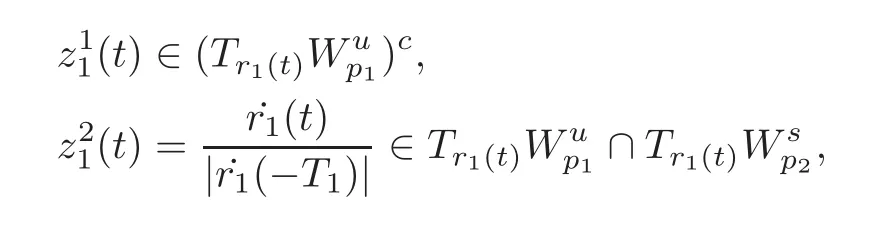
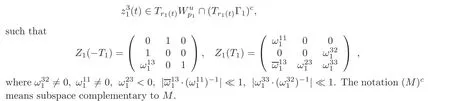
Also,there exists a fundamental solution matrixfor the system(2.3)satisfying

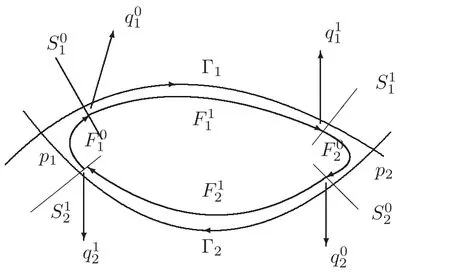
Figure 2 The cross-sections and Poincar´e map.

In order to obtain the Poincar´e map, first we should establish the relationship between the old coordinates

and their new coordinates

By the coordinate transformation hi(t)=ri(t)+Zi(t)Ni(t),we have

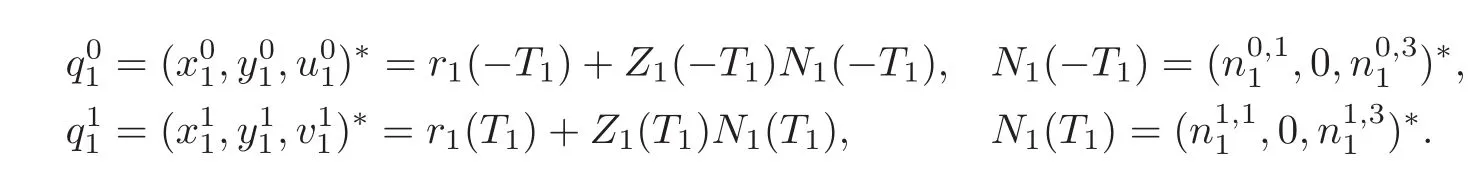
Then combining with the expressions of Zi(−Ti),Zi(Ti)(i=1,2),we obtain

and

For

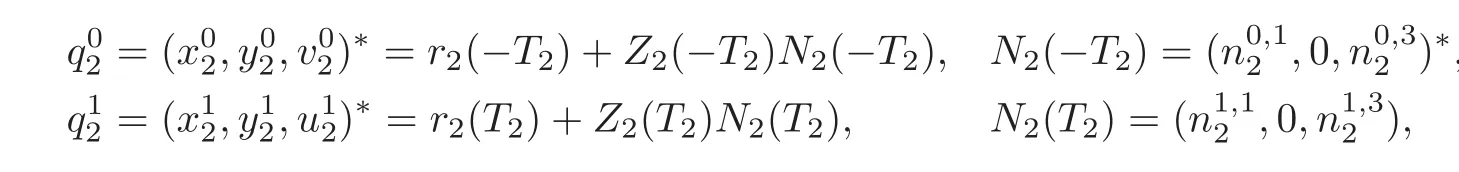
a similar calculation shows that

and

On the other hand,suppose that hi(t)=ri(t)+Zi(t)Ni(t)is the solution of(1.1)in the small tube neighborhood of Γi.Then substitute it into(1.1),and we have

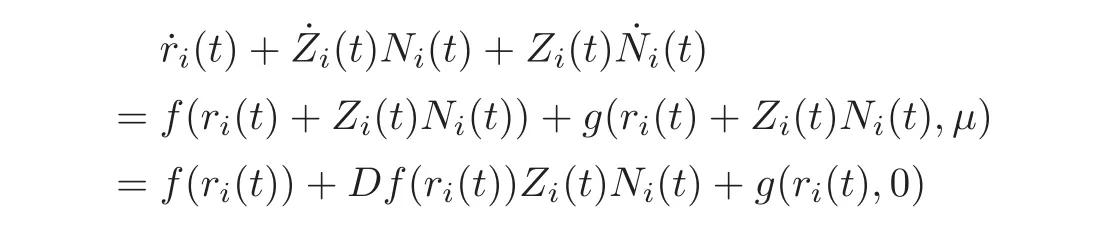
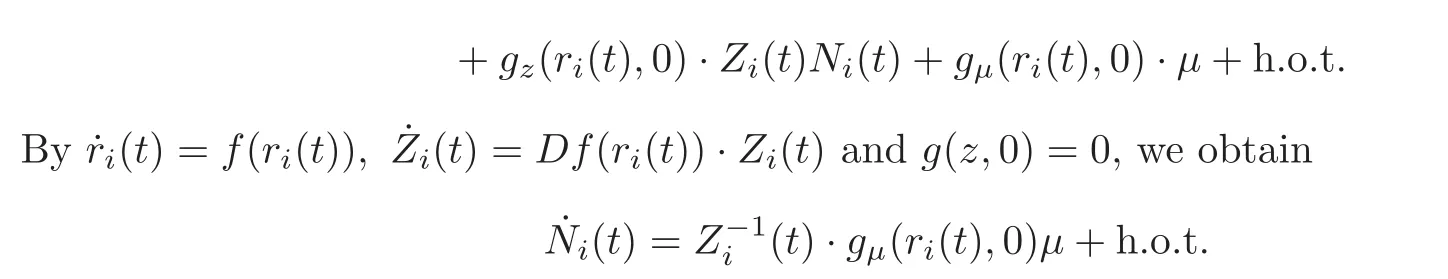
Integrating both sides of this equation from−Tito Ti,we have

which produce the global map

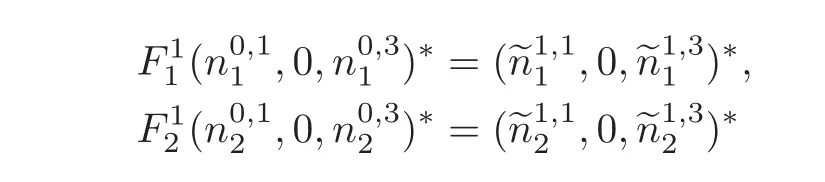
with the expression given by

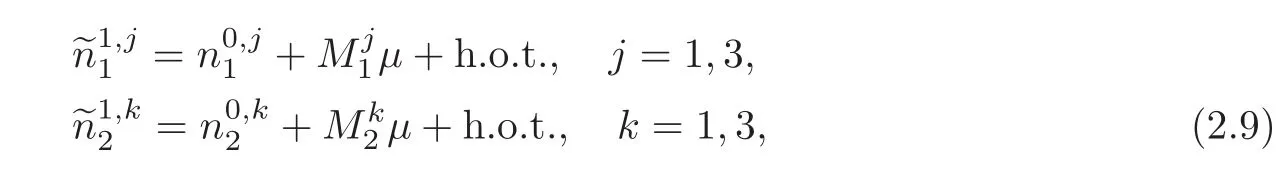
where

Remark 2.1Shilnikov variables were introduced by Shilnikov in 1968 to compute the local transition map near equilibria to leading order.Instead of solving an initial-value problem,solutions near the equilibrium are found using an appropriate boundary-value problem.Further information on Shilnikov variables can be found in[24,p.62]and[26].

Then,by(2.6),(2.8),(2.12)–(2.13),we obtain the successor functions

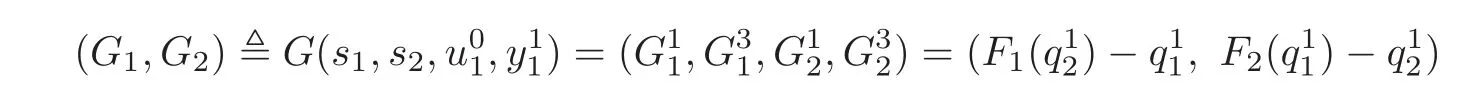
as follows:

By the implicit function theorem,solving the equation=0,we have

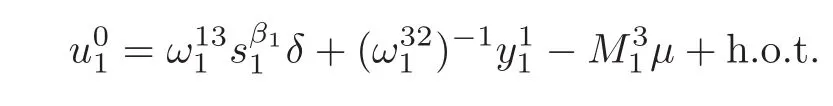
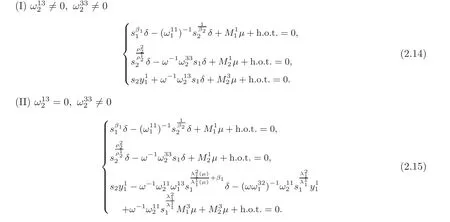
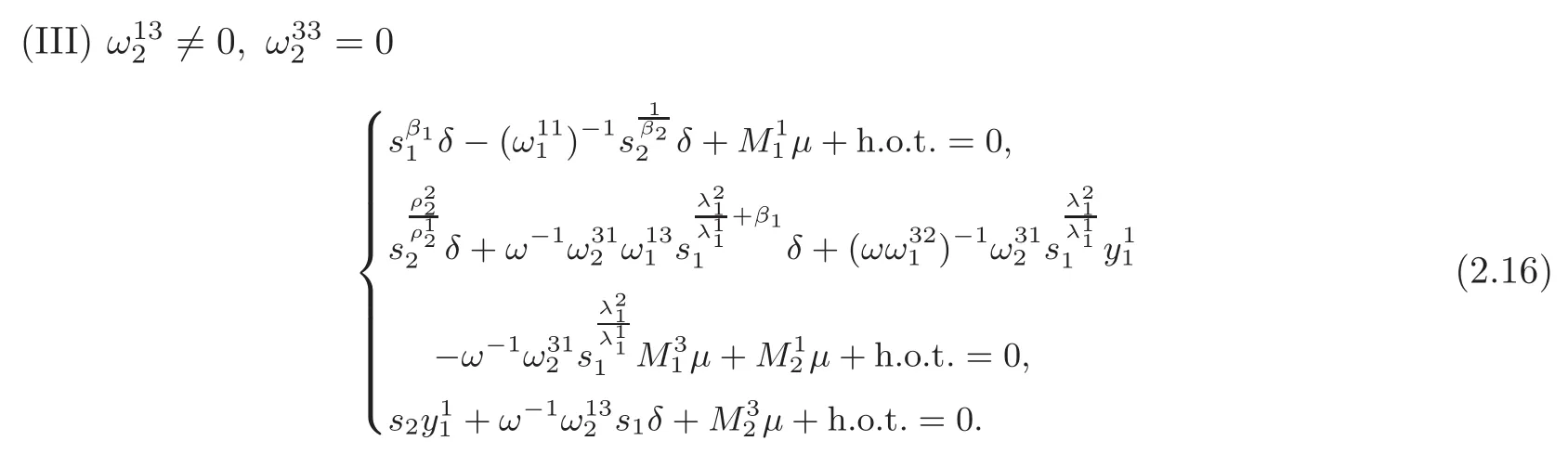
Remark 2.2Note that the solutions of(2.14)–(2.16)lose the uniqueners,and the solutions demonstrate different kinds of dynamical patterns corresponding to the different parameter regions,then equations(2.14)–(2.16)are called the bifurcation equation.

Remark 2.3For thefirst two cases,by some simple computation,we can obtain similar bifurcation results to that given in[17];so we omit it.While,in case(III),we will show that there are different bifurcation phenomena from that discussed in[17].Therefore,we will only focus on the third case.

3 Bifurcation Results

In this section we will study the bifurcation problem of the loop Γ under all hypotheses(H1)–(H5).The existence,coexistence and noncoexistence of periodic orbit,homoclinic loop and heteroclinic loop are discussed by studying the corresponding bifurcation equation.By establishing of local mapsandwe know that if s1=s2=0,then the heteroclinic loop of system(1.1)is persistent;if s1=0,s2＞0,then the system(1.1)has a loop homoclinic to p1;if s1＞0,s2=0,then the system(1.1)has a loop homoclinic to p2;if s1＞0,s2＞0,the system(1.1)has a periodic orbit.Then,we need only to consider the nonnegative solution s1and s2of the bifurcation equation.

Now we consider the persistence of the heteroclinic loop under small perturbation.is a codimension 3 surface with normal plane spanned by

atµ=0 such that the system(1.1)has a unique heterodimensional loop near Γ asµ ∈ L12,0 ＜ |µ|≪ 1,and≪1.In addition,because the y axis corresponds to the leading stable eigendirection,we easily get to know that if/=0,thenenters p2along y axis,that is,it can not exhibit orbitflip nearas t→ +∞.

A corresponding results about the existence of the homoclinic orbit connecting piis contained in the next theorems.

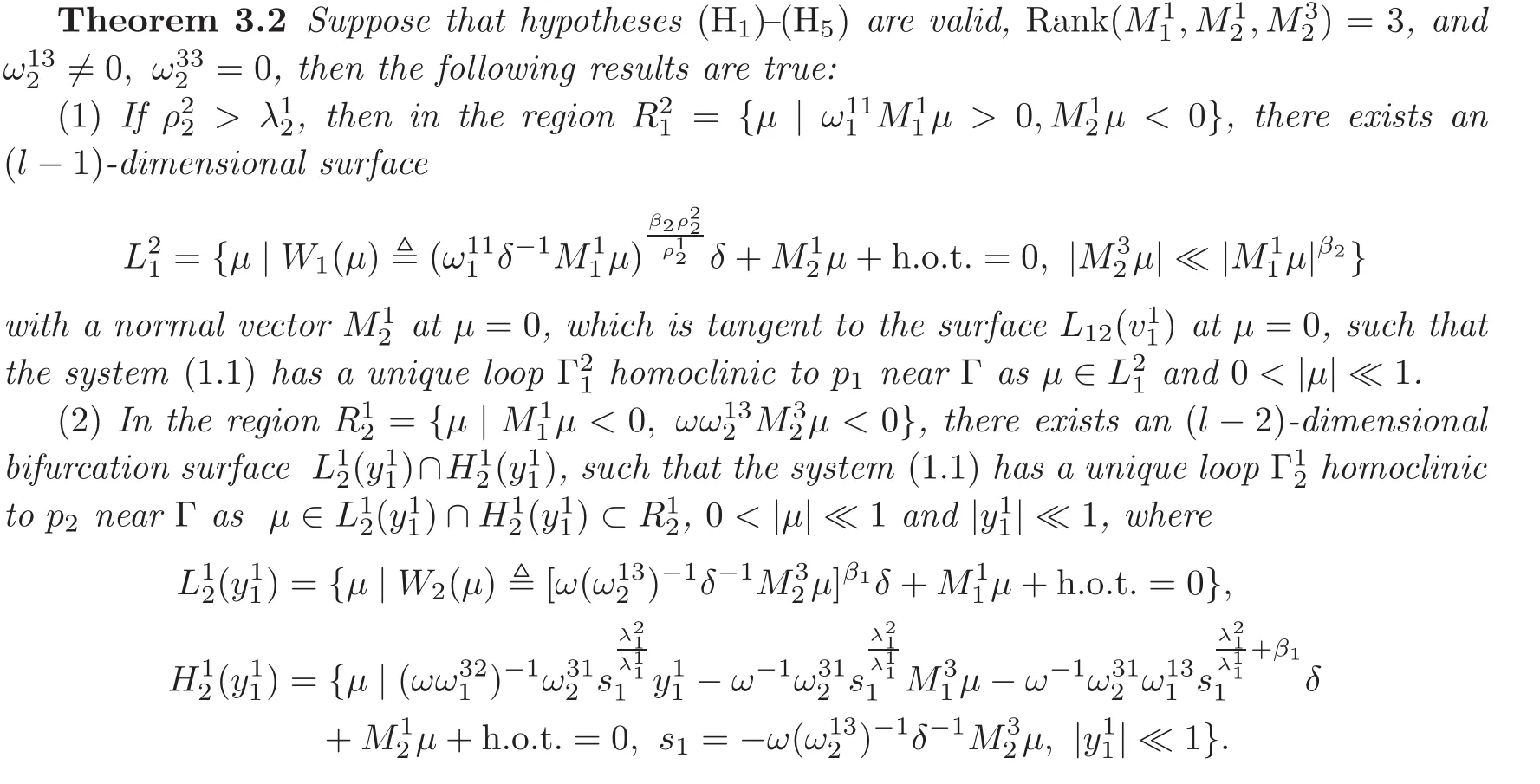
Proof(1)Assume that(2.16)has a solution s1=0,s2＞ 0,then it can be simplified into the following form:

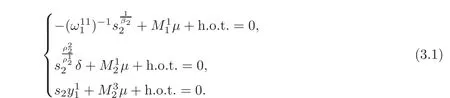
Next,relying on the analysis for the bifurcation equations(2.16),we discuss the coexistence of the heterodimensional cycle,homoclinic orbit and periodic orbit under small perturbation.

Theorem 3.3Suppose that hypotheses(H1)–(H5)are valid,Rank

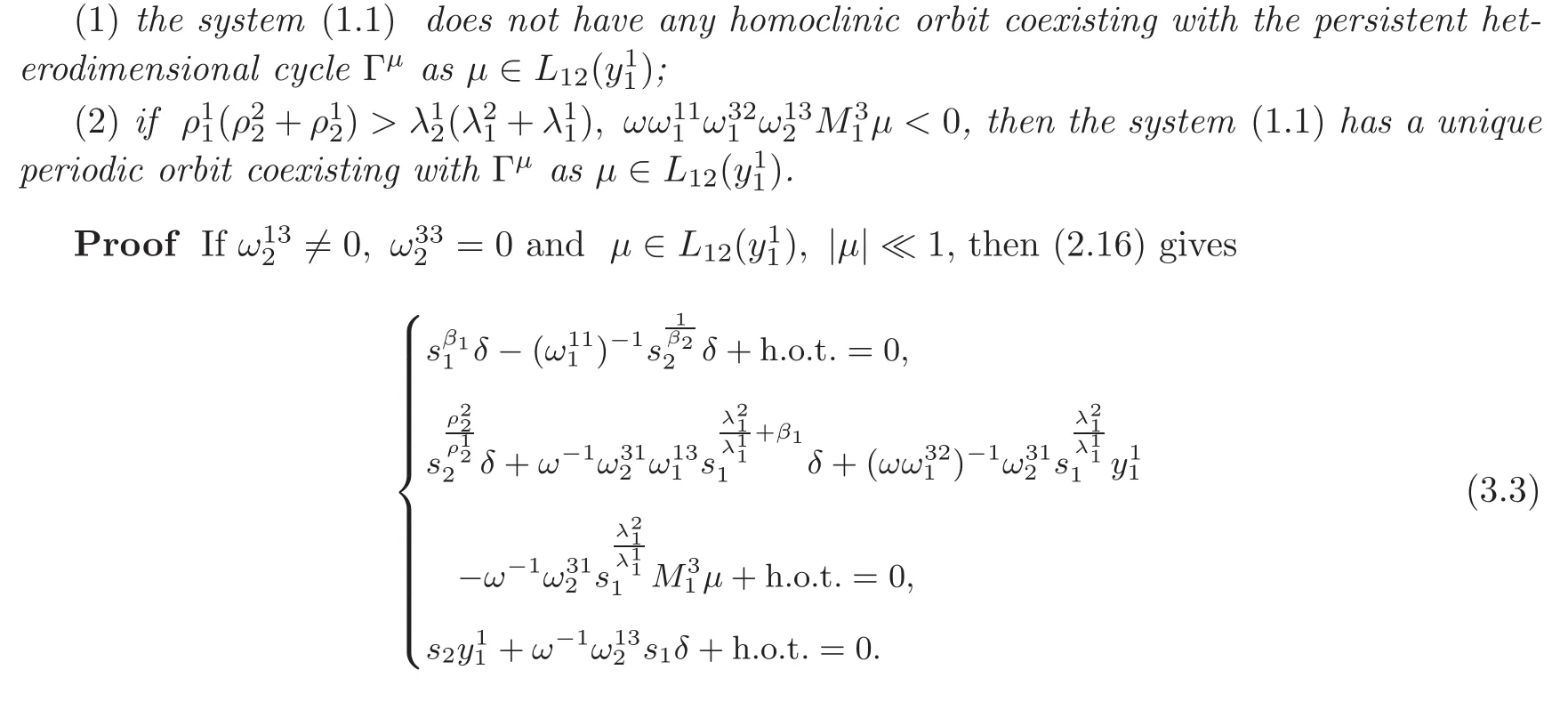
(1)By the first equation of(3.3),we have s2=+h.o.t.It is obvious that s2≥0 if s1≥ 0 and＞ 0,and s1=0 if and only if s2=0,so we conclude that(1.1)does not have any homoclinic loops forµ∈L12().

(2)On the other hand,by the third equation of(3.3),we have

By(H5),we have β1β2＜ 1,then 0 ＜ s1≪ 1 implies that≪ 1.Substituting the expressions of s2,into the second equation,we obtain

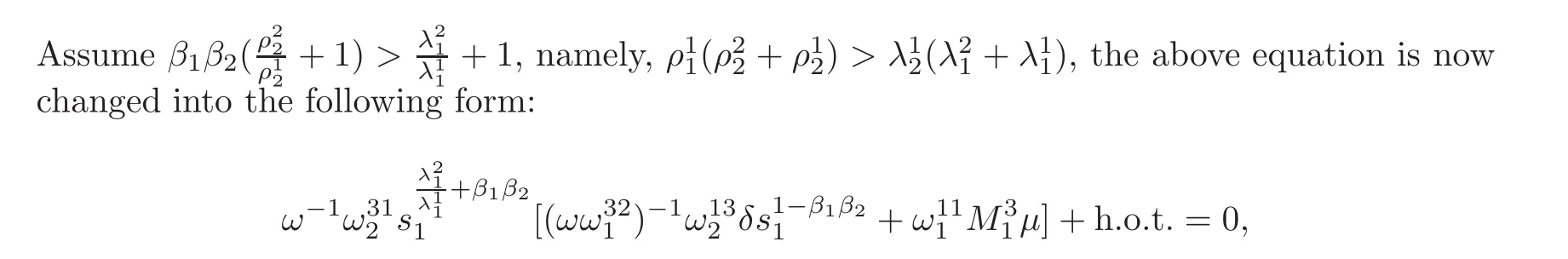
which has exactly two nonnegative solutions

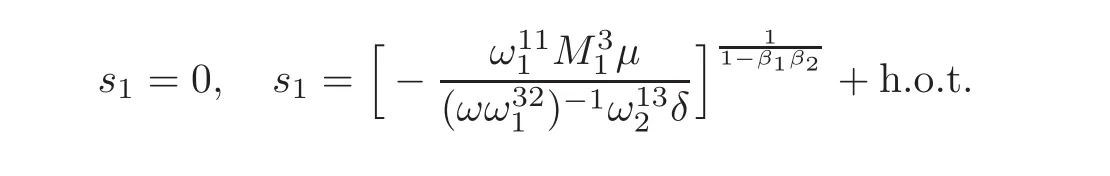
ProofUnder the hypotheses,the third equation of(2.16)shows that

Substituting it into the second equation of(2.16),we have

On the other hand,if 0≤s1≪ 1,µ∈and 0＜|µ|≪1,by thefirst equation of(2.16),we have

where

Then we have

With the analysis above,we know that each positive zero point s1of(s,µ)=0 corresponds to a unique pair of positive solutions(s1,s2)of the bifurcation equation(2.16).Then we obtain the conclusions.

4 Example

In this section,an example of vectorfield is given to show the existence of the system which has a nontransversal heterodimensional cycle with one orbitflip,and demonstrate how to use the method given in this paper to discuss the bifurcation problem.

Consider the following three-dimensional system

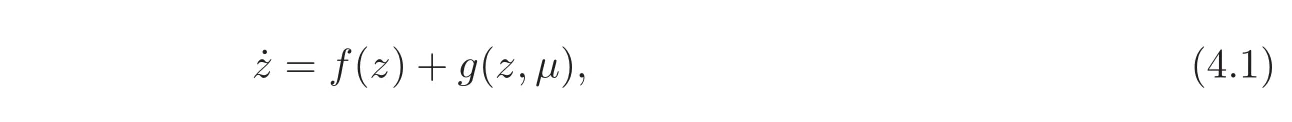
and its unperturbed system

Whenµ=0,the system(4.2)has equilibria

and a heteroclinic cycle Γ = Γ1∪ Γ2connecting p1and p2,where

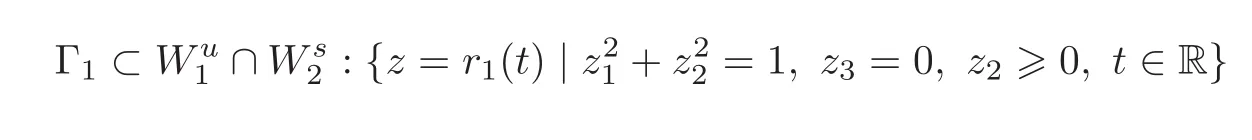
and

which is expressed by Γi={z=ri(t),t∈ R},i=1,2.Here

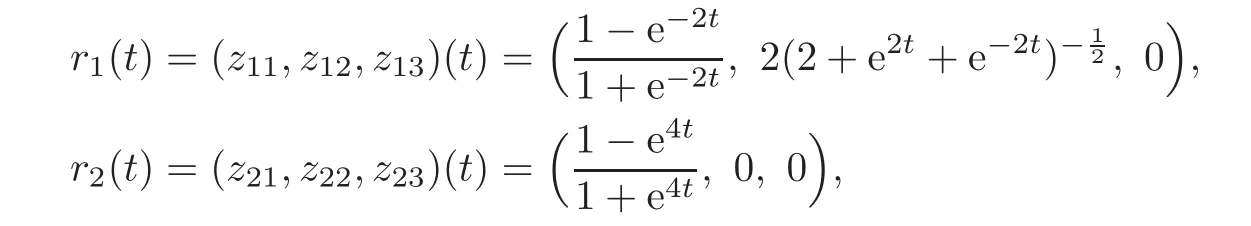
which satisfies r1(−∞)=r2(+∞)=P1,r1(+∞)=r2(−∞)=P2(see Figure 3).

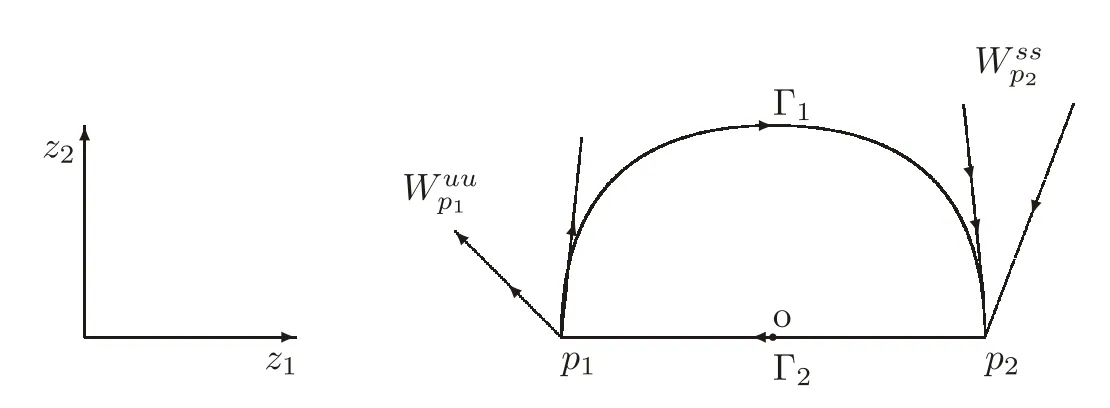
Figure 3 Γ1with orbit flip in positive direction.

Since

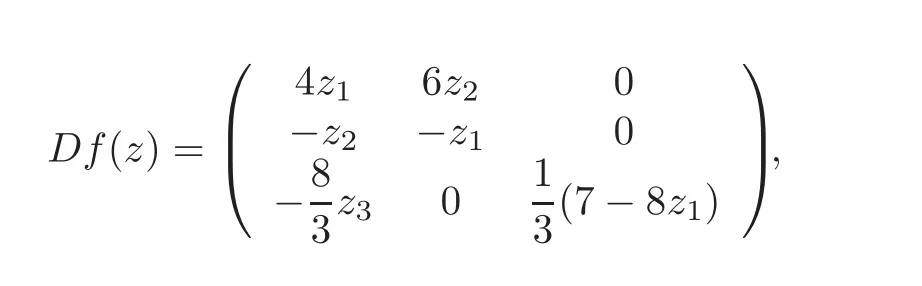
then we have

which means Γ = Γ1∪Γ2is a heterodimensional cycle and Γ1has orbitflip in positive direction;in other words,heteroclinic orbit Γ1enters the equilibrium p2along the strong stable direction z2as t→ +∞.Notice that Tr1(t)→ span{(0,1,0)∗,(0,0,1)∗},as t→ −∞,where(0,1,0,)∗,(0,0,1)∗are the unit eigenvectors of p1corresponding to the positive eigenvalue 1,5,respectively.Then the 2-dimensional unstable manifolds of p1coincide with the 2-dimensional stable manifolds of p2,that is,Γ1is a nontransversal orbit.

Let 0＜δ≪1 and Ti(i=1,2)be large enough such that

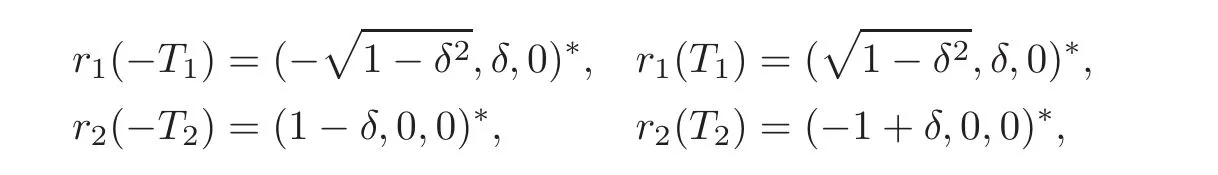
then we have

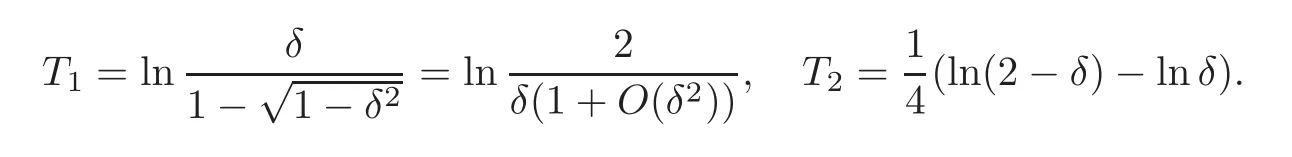
Now we consider the linear variational system of unperturbed system(4.2)along Γi(i=1,2):

and its adjoint system

where

Next we discuss the persistent of the heterodimensional cycle of(4.2),by a similar computation given in Section 2,we know that the persistent of the heterodimensional cycle is related with elements in Zi(Ti),Zi(−Ti)(i=1,2)as well asFirstly,we consider the fundamental solution matrix Z1(t)and Φ1(t).

One fundamental solution matrix for(4.3)is

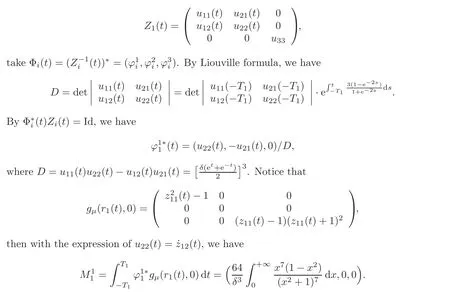
Next we consider Z2(t)and Φ2(t).By Df(r2(t)),we obtain one fundamental solution matrix for(4.3)as follows:

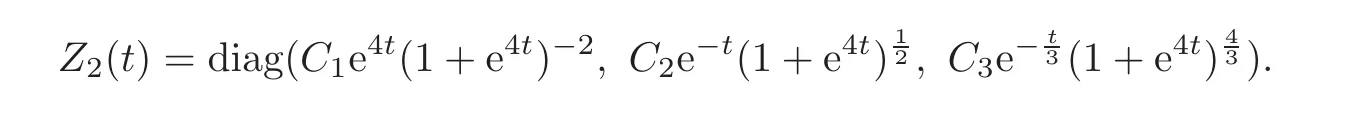
Thus,we obtain

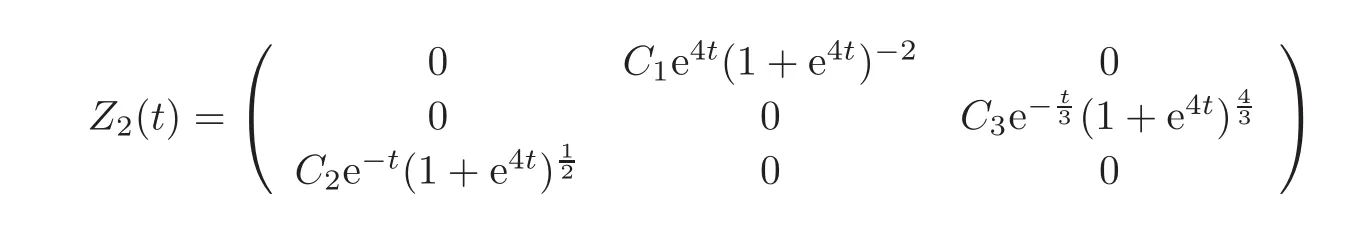
for t≤−T2,and

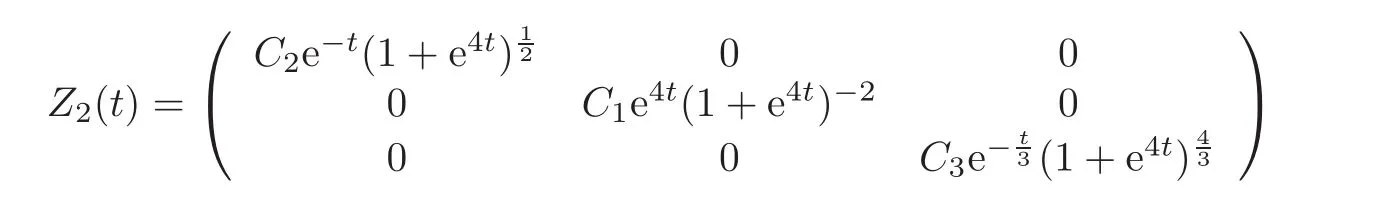
for t≥ T2.By the initial values Z2(−T2)given in Section 2,we have

Correspondingly,by performing the coordinates transformation in the small neighborhood of Pi,we have

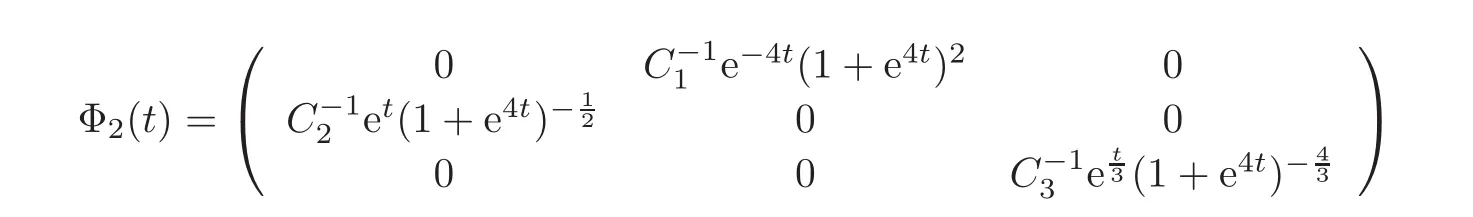
for t∈R.Note that

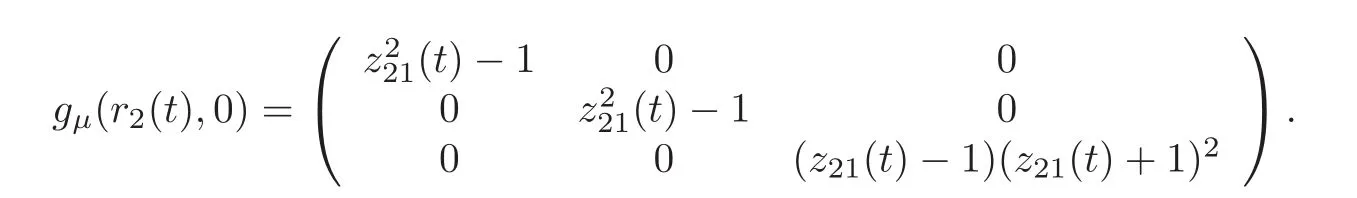
Hence,we can calculate

[1]Homburg,A.J.and Sandstede,B.,Homoclinic and heteroclinic bifurcations in vectorfields,Handbook of Dynamical Systems,Broer,Henk(ed.)et al.,3,Amsterdam:Elsevier,2010,379–524.

[2]Han,M.A.and Zhu,H.P.,The loop quantities and bifurcations of homoclinic loops,J.Differ.Equ.,234,2007,339–359.

[3]Chow,S.N.,Jiang,M.and Lin,X.B.,Traveling wave solutions in coupled Chua’s circuits,part I:Periodic solutions,J.Applied.Analysis and Computation,3,2013,213–237.

[4]Yanagida,E.,Branching of double pulse solutions from single pulse solutions in nerve axon equations,J.Differ.Equ.,66,1987,243–262.

[5]Sandstede,B.,Constructing dynamical systems having homoclinic bifurcation points of codimension two,J.Dyn.Differ.Equ.,9,1997,269–288.

[6]Naudot,V.,A strange attractor in the unfolding of an orbit-flip homoclinic orbit,Dyn.Syst.,17,2002,45–63.

[7]Golmakani,A.and Homburg,A.J.,Lorenz attractors in unfoldings of homoclinic-flip bifurcations,Dyn.Syst.,26,2011,61–76.

[8]Liu,X.B.,Wang,Z.Z.and Zhu,D.M.,Bifurcation of rough heteroclinic loop with orbitflips,Int.J.Bifurc.Chaos,22,2012,1250278-1.

[9]Newhouse,S.E.and Palis,J.,Bifurcations of Morse-Smale dynamical systems,Dynamical Systems,Academic Press,New York,1973,303–366.

[10]Fern´andez-S´anchez,F.,Freire,E.and Rodr´iguez-Luis,A.J.,Bi-spiraling homoclinic curves around a T-point in Chua’s circuit,Int.J.Bifurc.Chaos,14,2004,1789–1793.

[11]Algaba,A.,Freire,E.,Gamero,E.and Rodr´iguez-Luis,A.J.,A tame degenerate Hopf-pitchfork bifurcation in a modified van der Pol-Duffing oscillator,Nonlinear Dyn.,22,2000,249–269.

[12]Bykov,V.V.,The bifurcations of separatrix contours and chaos,Physica D,62,1993,290–299.

[13]Rademacher,J.D.M.,Homoclinic orbits near heteroclinic cycles with one equilibrium and one periodic orbit,J.Differ.Equ.,218,2005,390–443.

[14]Bonatti,C.,Diaz,L.J.,Pujals,E.and Rocha,J.,Robust transitivity and heterodimensional cycles,Asterisque,286,2003,187–222.

[15]Diaz,L.J.and Rocha,J.,Heterodimensional cycles,partial hyperbolity and limit dynamics,Fund.Math.,174,2002,127–186.

[16]Lamb,J.S.W.,Teixeira,M.A.and Webster,K.N.,Heteroclinic bifurcations near Hopf-zero bifurcation in reversible vector fields in R3,J.Differ.Equ.,219,2005,78–115.

[17]Liu,D.,Geng,F.J.and Zhu,D.M.,Degenerate bifurcations of nontwisted heterodimensional cycles with codimension 3,Nonlinear Analysis,68,2008,2813–2827.

[18]Liu,X.B.,Bifurcations near the weak type heterodimensional cycle,Int.J.Bifur.Chaos,9,2014,1450112,18 pages.

[19]Lu,Q.Y.,Qiao,Z.Q.,Zhang,T.S.and Zhu,D.M.,Heterodimensional cycle bifurcation with orbit-flip,Int.J.Bifur.Chaos,20,2010,491–508.

[20]Fern´andez-S´anchez,F.,Freire,E.and Rodr´iguez-Luis.A.J.,Bi-spiraling homoclinic curves around a T-point in Chua’s circuit,Int.J.Bifur.Chaos,14,2004,1789–1793.

[21]Zhu,D.M.and Xia,Z.H.,Bifurcations of heteroclinic loops,Sci.China Ser.A,41,1998,837–848.

[22]Liu,X.B.,Homoclinicflip bifurcations accompanied by transcritical bifurcation,Chin.Ann.Math.,Ser.B,6,2011,905–916.

[23]Xu,Y.C.and Zhu,D.M.,Bifurcations of heterodimensional cycles with one orbitflip and one inclinationflip,Nonlinear Dyn.,60,2010,1–13.

[24]Shilnikov,L.P.,Shilnikov,A.L.,Turaev,D.V.and Chua,L.O.,Methods of Qualitative Theory in Nonlinear Dynamics,Part I,World Scientific,New Jersey,1998.

[25]Homburg,A.J.and Knobloch,J.,Multiple homoclinic orbits in conservative and reversible systems,Trans.Am.Math.Soc.,4,2006,1715–1740.

[26]Deng,B.,Sil’nikov problem,exponential expansion,strong λ-Lemma,C1-linearization and homoclinic bifurcation,J.Differ.Equ.,79,1989,189–231.