Exponential Convergence to Time-Periodic Viscosity Solutions in Time-Periodic Hamilton-Jacobi Equations∗

Kaizhi WANG

1 Introduction

Consider the time-periodic Hamilton-Jacobi equation

where M is a closed(i.e.,compact without boundary)and connected smooth manifold of dimension m.We choose,once and for all,a C∞Riemannian metric on M.It is classical that there is a canonical way to associate to it a Riemannian metric on TM.The Hamiltonian H(x,p,t):T∗M × R → R,defined by H(x,p,t)=,is 1-periodic in t,where 〈·,·〉xrepresents the canonical pairing between the tangent and cotangent space,and L(x,v,t):TM ×R→R is a C2Lagrangian and satisfies the following conditions:

(H1)Periodicity.L is 1-periodic in the R factor.

(H2)Positive Definiteness.For each x∈M and each t∈R,the restriction of L to TxM×{t}is strictly convex in the sense that its Hessian second derivative is everywhere positive definite.

(H4)Completeness of the Euler-Lagrange Flow.The maximal solutions of the Euler-Lagrange equation,which in local coordinates is

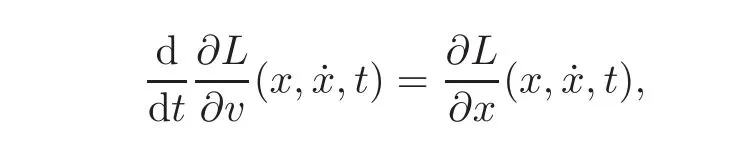
are defined on all of R.

Such a Lagrangian L is usually called a time-periodic Tonelli Lagrangian in the literature.Without loss of generality,we will from now on always assume that the Ma˜n´e critical value(see[12])of L is 0.

For a given time-periodic Tonelli Lagrangian L,it is well known that the function U:M ×[0,+∞)→R defined by U(x,t)=Ttu0(x)is the unique viscosity solution of the Cauchy problem

where u0:M→R is a continuous function and Tt:C(M,R)→C(M,R),t≥0 is the Lax-Oleinik operator(see Section 2 for a definition)associated with the Lagrangian L(see[9]for instance).

(H5)The Aubry set of L consists of one hyperbolic 1-periodic orbit.

For any given time-periodic Tonelli Lagrangian L satisfying(H5),we show that for each u0∈C(M,R),the unique viscosity solution U(x,t)of the Cauchy problem(1.2)converges exponentially fast to a 1-periodic viscosity solution of(1.1)as t→+∞.

The main result of this paper is as follows.

Theorem 1.1If a time-periodic Tonelli LagrangianL:TM ×R→Rsatisfies(H5),then there existsρ＞0such that for eachu0∈C(M,R),there exists a constantK＞0and a1-periodic viscosity solutionof(1.1)such that

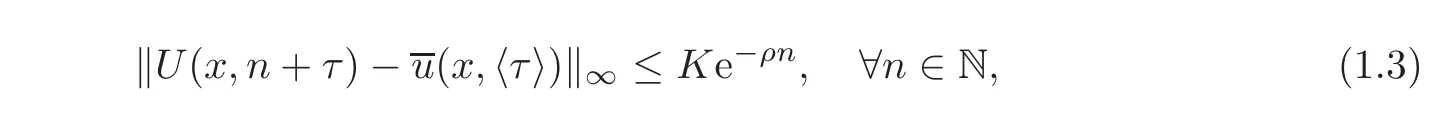
whereτ∈ [0,1],〈τ〉= τ mod 1,and‖ ·‖∞denotes the supremum norm in the spaceC(M ×[0,1],R).

Remark 1.1In fact,the unit circle and h denotes the(extended)Peierls barrier(see Section 2 for a definition).

Remark 1.2Inequality(1.3)implies thatK1＞ 0 is a constant and ‖·‖0denotes the supremum norm in the space C(M,R).

Remark 1.3The essence of Theorem 1.1 is that the Lax-Oleinik operators possess an exponential convergence rate under the assumptions(H1)–(H5).See[8,16–18]for various results on the rate of convergence of the Lax-Oleinik operators for the autonomous case.

Remark 1.4In[15],S´anchez-Morgado provides a similar result to Theorem 1.1 for M=Tm,where Tmdenotes the flat m-torus.Our method here is totally different from that used in[15].

2 Preliminaries

The methods here are inspired from Mather-Ma en´e-Fathi theory(see[4–7,10–14])on Tonelli Lagrangian systems.We introduce the notations used in the sequel and review some definitions and results of Mather-Ma en´e-Fathi theory in this section.

We view S as a fundamental domain in R:I=[0,1]with the two endpoints identified.The unique coordinate s of a point in S will belong to I=[0,1).The standard universal covering projection π :R → S takes the formusual Euclidean norm.

The Euler-Lagrange equation generates a flow of diffeomorphisms:TM×S → TM ×S,t∈ R,defined by

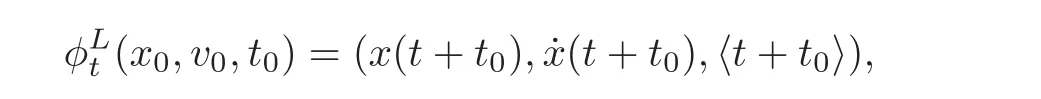
where x:R→M is the maximal solution of the Euler-Lagrange equation with initial conditions x(t0)=x0,˙x(t0)=v0.The completeness and periodicity conditions grant that this correctly defines a flow on TM ×S.

Consider the action functional ALfrom the space of continuous and piecewise C1curves γ :[a,b]→ M,defined by

where dγ :[a,b]→ TM denotes the differential of γ.

Recall the definition of the Lax-Oleinik operators Ttassociated with L.For each t≥ 0 and each u0∈C(M,R),let

for all x ∈ M,where the infimum is taken among the continuous and piecewise C1paths γ :[0,t]→ M with γ(t)=x.For each t≥ 0,Ttis an operator from C(M,R)to itself.

As done by Mather in[14],it is convenient to introduce,for all t＜ t′∈ R and x,x′∈ M,the following quantity:

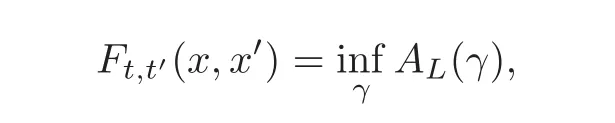
where the infimum is taken over the continuous and piecewise C1paths γ :[t,t′]→ M such that γ(t)=x and γ(t′)=x′.For all t ＜ t′∈ R and all x,x′∈ M,there exists a continuous and piecewise C1path:[t,t′]→ M with γ(t)=x and γ(t′)=x′such that Ft,t′(x,x′)=AL(γ)(see[13,Tonelli’s Theorem]).Such a curve is called a Tonelli minimizer(for the fixed endpoint problem).The function F:R × R × M × M → R,(t,t′,x,x′) → Ft,t′(x,x′)is Lipschitz and bounded on{t′≥ t+1}(see for example[2,Lemma 3.3]).

Following Ma en´e[12]and Mather[14],define the action potential and the extended Peierls barrier as follows.

Action Potential.For each(s,s′) ∈ S × S,let

for all(x,x′)∈ M × M,where the infimum is taken on the set of(t,t′) ∈ R2such that s= 〈t〉,s′= 〈t′〉and t′≥ t+1.

Extended Peierls Barrier.For each(s,s′)∈ S × S,let

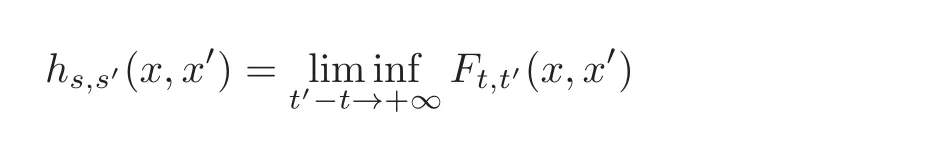
for all(x,x′)∈ M ×M,where the liminf is restricted to the set of(t,t′)∈ R2such that s= 〈t〉,s′= 〈t′〉.The function h:S × S × M × M → R,(s,s′,x,x′) → hs,s′(x,x′)is Lipschitz(see[3,Proposition 2]for details).

A continuous and piecewise C1curve γ:R →M is called global semi-static if

for all[t,t′]⊂ R.An orbit(dγ(σ),〈σ〉)is called global semi-static if γ is a global semi-static curve.The Ma en´e seteN0is the union in TM × S of the images of global semi-static orbits.A continuous and piecewise C1curve γ:R→ M is called global static if

for all[t,t′]⊂ R.An orbit(dγ(σ),〈σ〉)is called global static if γ is a global static curve.The Aubry setis the union in TM×S of the images of global static orbits.For a time-periodic Tonelli Lagrangian satisfying(H5),we have

A time-periodic Tonelli Lagrangian L is called regular,if the liminf in the definition of the functions hs,s′is a limit for all s,s′,x,x′.According to[2,Lemma 5.4],a time-periodic Tonelli Lagrangian L satisfying(H5)is regular.Thus,under the assumptions of Theorem 1.1,we have

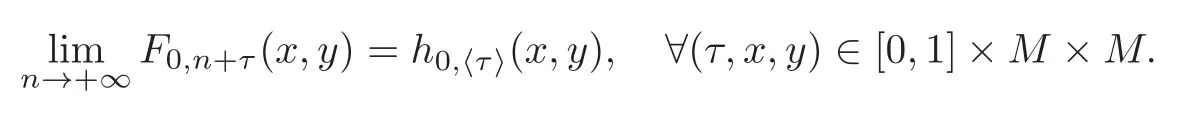
Since the family of functions{F0,n+·(·,·)}nis equi-Lipschitzian,we have

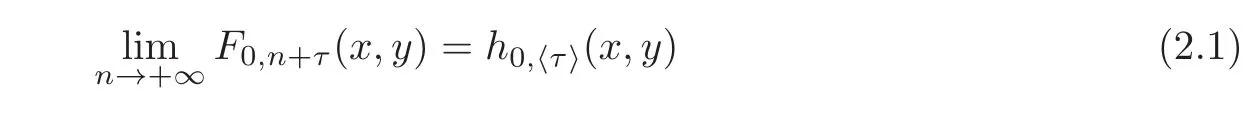
uniformly on(τ,x,y)∈ [0,1]×M × M.Note that for each u0∈ C(M,R),each τ∈ [0,1],each n∈N and each x∈M,we have

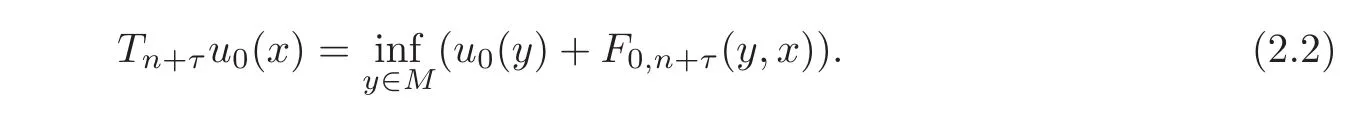
From(2.1)–(2.2),it is easy to see that

In view of(2.3),the functionin Theorem 1.1 has the form

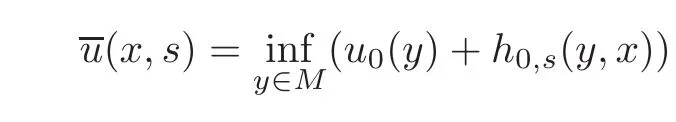
for all(x,s)∈ M × S.Furthermore,from[17,Propositions 3.12–3.13],is exactly the set of 1-periodic viscosity solutions or backward weak KAM solutions of(1.1).Now we recall the definition of the weak KAM solution of(1.1).

A backward weak KAM solution of the Hamilton-Jacobi equation(1.1)is a function w:M×S→R such that w is dominated by L,i.e.,

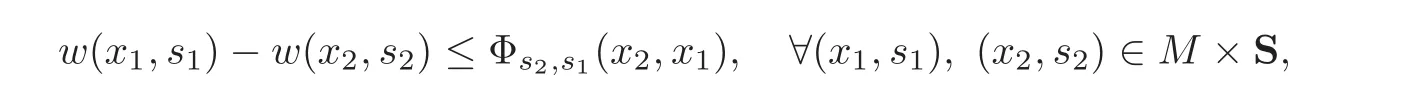
and for every(x,s)∈ M × S,there exists a curve γ :(−∞, es]→such that

The equivalent classes of this relation are called static classes.Let A be the set of static classes.For each static class Γ ∈ A,choose a point(x,0)∈ Γ and let A0be the set of such points.Under the assumptions of Theorem 1.1,A0consists of only one point,denoted by(p,0)∈A0.Thus,for each backward weak KAM solution w of(1.1),we have

for all(x,s)∈M×S(see[3,Theorem 7]).

Proposition 2.1Under the assumptions of Theorem1.1,letVbe a neighborhood of the Aubry seinTM×S.Given0＜a1＜a2＜1,there existsT＞0such that ifn≥T,n∈N,τ∈ [0,1],andγ :[0,n+τ]→ Mis a Tonelli minimizer for thefixed point problem,then

Based on the above arguments,it is sufficient to show that γ is a global semi-static curve.We prove it by contradiction.Otherwise,there would be j1,j2∈N such that

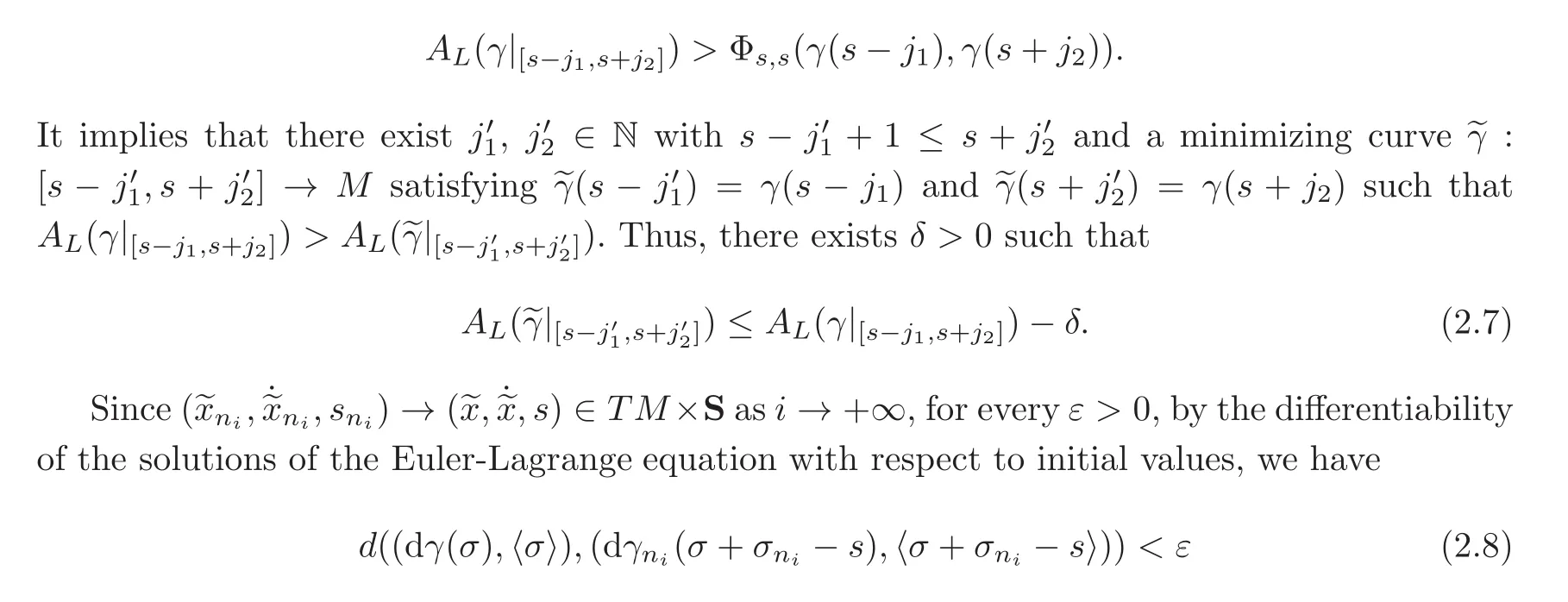
for all σ ∈ [s−j1,s+j2]and i large enough.Using the periodicity of L,we have

In view of(2.8)–(2.9),we have

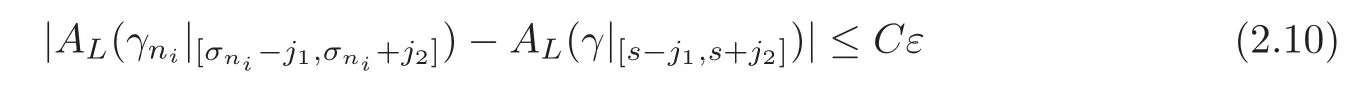
for some constant C ＞ 0 independent of ε and sufficiently large i.Since ε may be taken arbitrary small,from(2.7)and(2.10)we obtain

provided that i is large enough.

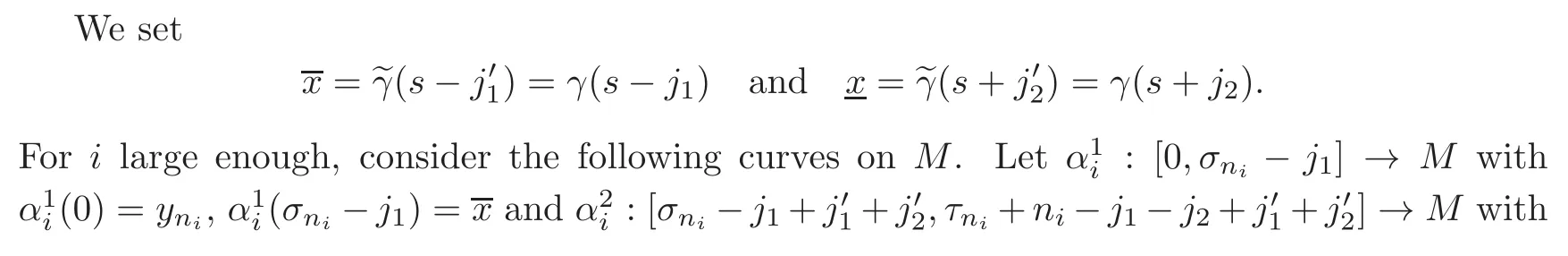
where DLip＞ 0 is a Lipschitz constant of Ft,t′which is independent of t,t′with t+1 ≤ t′(see[2,Lemma 3.3]).

Note that

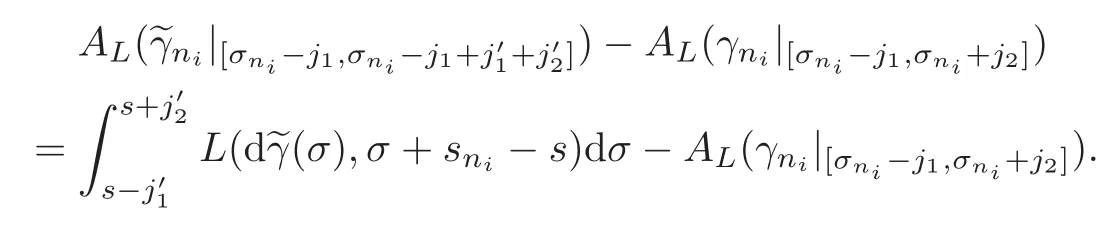
Since sni→s as i→+∞,

for i large enough.Hence,

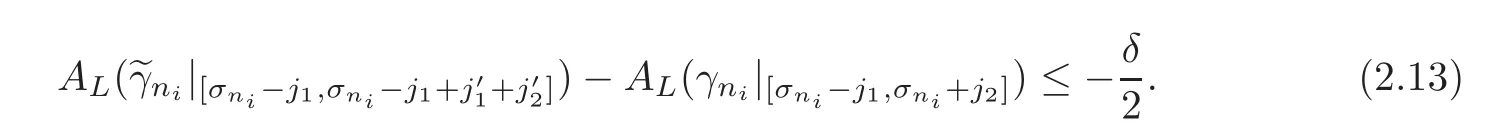
From the Lipschitz property of Ft,t′and(2.8),we find

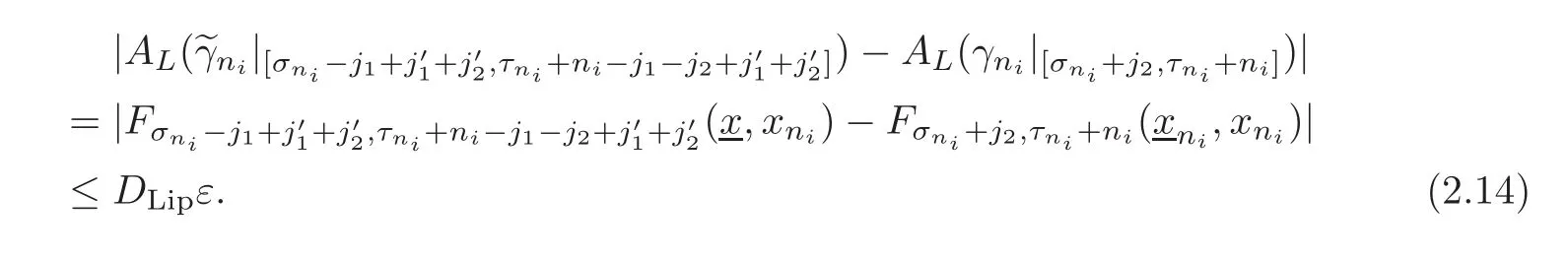
Since ε may be taken arbitrary small,from(2.12)–(2.14),we have

for i large enough.

Since

from(2.1)and the Lipschitz property of h,we have

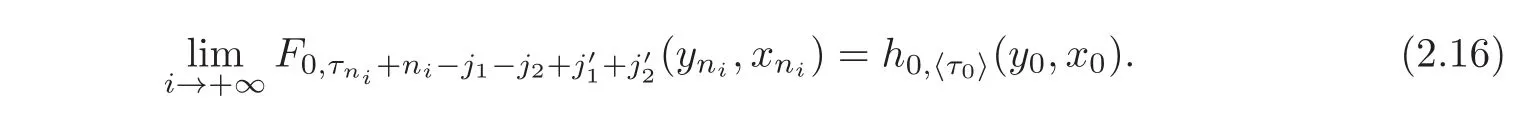
Combining(2.6)and(2.15)–(2.16),we have

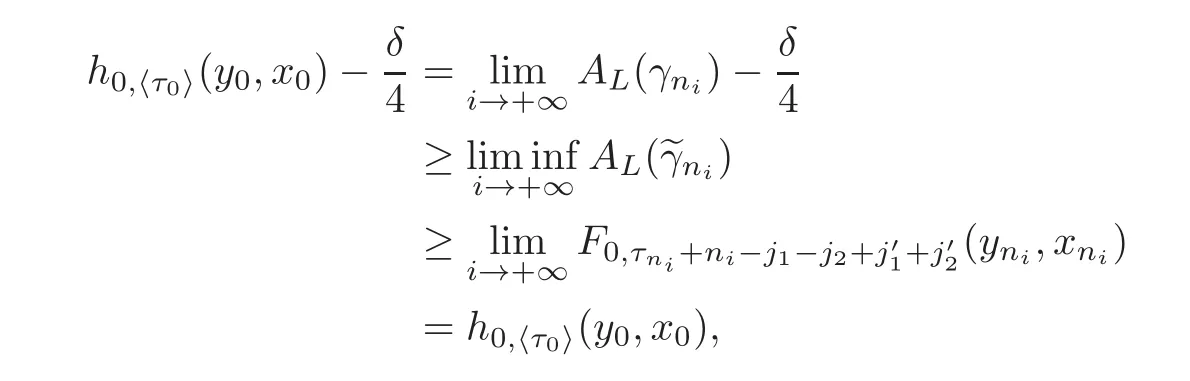
a contradiction.This contradiction shows that γ is global semi-static,which completes the proof of the proposition.

3 Proof of the Main Result

Let(p,vp,0)be the unique point inwith Π(p,vp,0)=(p,0)∈ A0,where Π :TM ×S1→M×S denotes the projection.By(H5)the Aubry setconsists of one hyperbolic 1-periodic orbit,denoted by Γ(p,vp,0)=(dγp(σ),〈σ〉),σ ∈ R.

Proof of Theorem 1.1Our purpose is to show that there exists ρ ＞ 0 such that for each u0∈C(M,R),there exists K＞0 such that the following two inequalities hold:

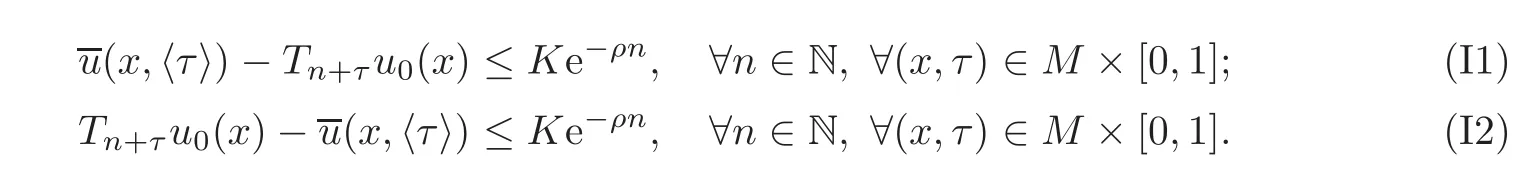
Step 1We first prove inequality(I1).For any given y ∈ M,h0,·(y,·)is a backward weak KAM solution of(1.1).In view of(2.4),we have

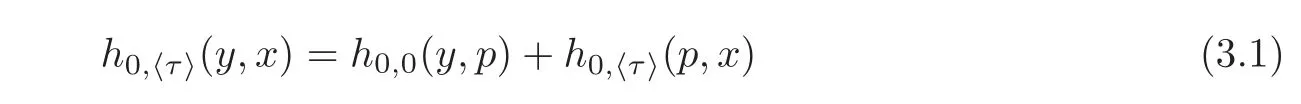
for all(x,τ)∈M ×[0,1].Given u0∈C(M,R)and(x,τ)∈M ×[0,1],it is easy to see that for each n ∈ N,there exists a minimizing extremal curve γn:[0,τ+n]→ M such that γn(τ+n)=x and

In view of(3.1),we have

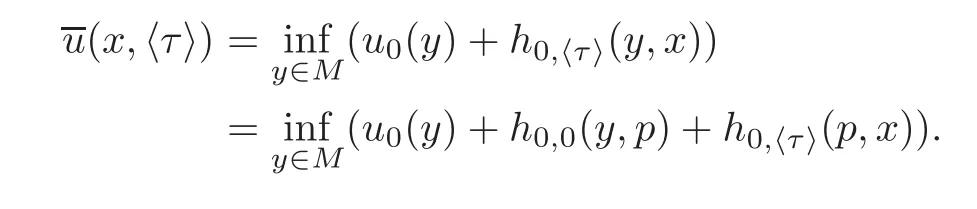
Thus,we have

where CLip＞0 is a Lipschitz constant of h.From(3.2)and(3.4),we have

We now estimate the term in the right-hand side of(3.5).Consider the Poincar´e map for the time-periodic Lagrangian system L,

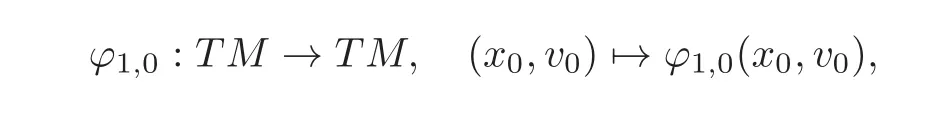
where ϕt,0(x0,v0)=(x(t),(t))and x(t)denotes the solution to the Euler-Lagrange equation with initial conditions x(0)=x0,(0)=v0.Obviously,easy to see that(p,vp)is a hyperbolic fixed point of ϕ1,0.According to the Hartman-Grobman theorem,the Poincar´e map ϕ1,0is locally conjugate to its linear part at the hyperbolic fixed point(p,vp).More precisely,there exist a neighborhood V(p,vp)of(p,vp)in TM as well as a neighborhood U(0)of 0 in T(p,vp)(TM)and a homeomorphism f:V(p,vp)→U(0),such that

Furthermore,there exists 0 ＜ α ＜ 1 such that f and f−1are α-Hö lder continuous(see[1]).Denote for brevity P=(p,vp).As the problem here is a local one,we can,using a local chart,suppose that ϕ1,0is a map from R2mto itself with P as a hyperbolic fixed point.

Let B(P)be a sufficiently small neighborhood of P in R2msuch that B(P)⊂ V(P)=V(p,vp).We choose a tubular neighborhood WΓof Γ such that for each(q,v,〈σ〉) ∈ Γ,d((q,v,〈σ〉),∂WΓ)= κ,where ∂WΓdenotes the boundary of WΓand κ is a positive constant small enough such that for each(q,v,0)∈WΓ,(q,v)∈B(P).For the tubular neighborhood WΓ,applying Proposition 2.1,there exists T＞0 such that for n∈N with n≥T,we have

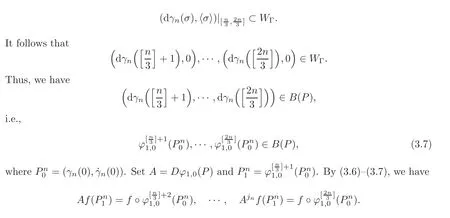
for n large enough,where C1＞0 is a constant.Therefore,there exists a constant C2＞0 independent of u0∈ C(M,R)and(x,τ)∈M ×[0,1]such that

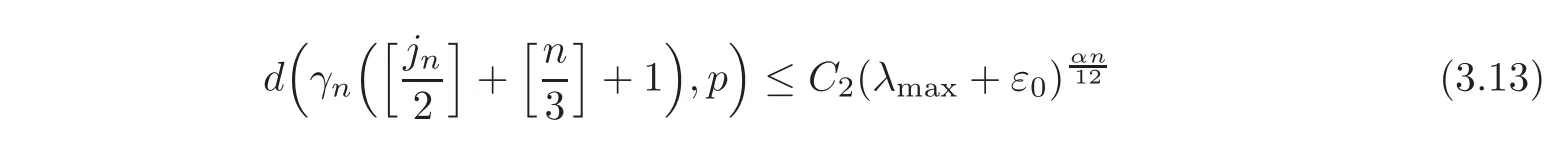
for n large enough.Note that the above estimate is independent of(x,τ).By(3.5)and(3.13),for sufficiently large n,we have

Hence,there exists a constant C3＞0 such that

where the constant C3depends on u0.Since 0 ＜ λmax+ ε0＜ 1,there exists ρ1＞ 0 such that(λmax+ ε0)=e−ρ1.Thus,we have

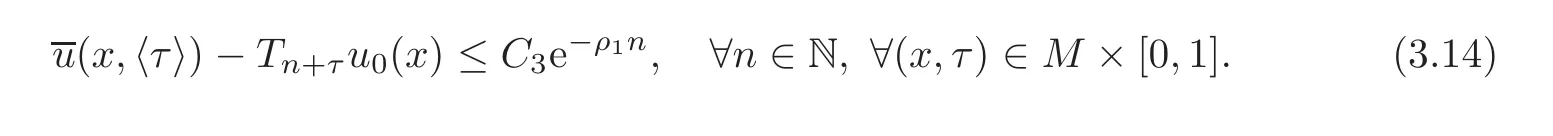
Step 2We now prove inequality(I2).Given u0∈C(M,R)and(x,τ)∈M ×[0,1],there exists y∈M such that

To prove(I2),it suffices to show that for n ∈ N large enough,we can find a curve η :[0,τ+n]→ M with η(0)=y and η(τ+n)=x,such that

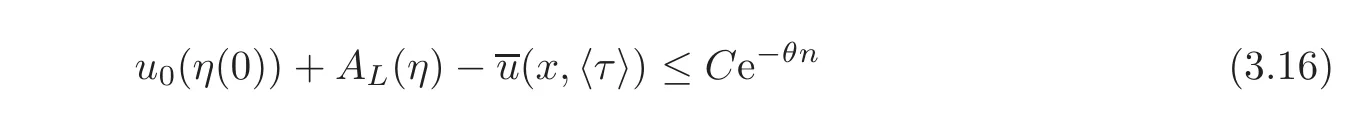
for some constants C,θ＞0 independent of u0∈C(M,R),(x,τ)∈M ×[0,1]and n∈N.In fact,for n∈N large enough,if such a curve exists,then we have

which immediately implies the desired inequality(I2).

Our task now is to construct the curve mentioned above.Since h0,·(p,·)is a backward weak KAM solution of(1.1),there is a curvesuch that

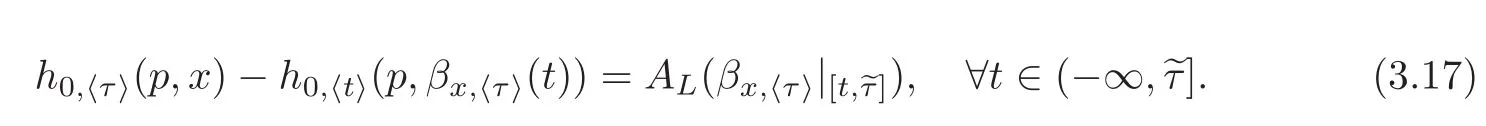
It is clear that βx,〈τ〉is a minimizing curve.From[2,Lemma 3.9],the α-limit set for any minimizing orbit is contained in the Aubry set.Sinceconsists of one hyperbolic 1-periodic orbit Γ,the α-limit set for(dβx,〈τ〉(σ),〈σ〉)is exactly Γ.Similarly,since −h·,0(·,p)is a forward weak KAM solution of(1.1),there exists a curve

Moreover,ωy,0is a minimizing curve and the ω-limit set for(dωy,0(σ),〈σ〉)is also the hyperbolic 1-periodic orbit Γ(see[2,Lemma 3.9]).

Since Γ is a hyperbolic 1-periodic orbit,for the tubular neighborhood WΓthere exist constants T1＞0 and C4＞0,such that

for all σ＞T1,and

for all σ ＜ −T1,where T1and C4depend only on WΓ,and µ denotes the smallest positive Lyapunov exponent of Γ.

We are now in a position to construct the curve η.For n ∈ N large enough such that

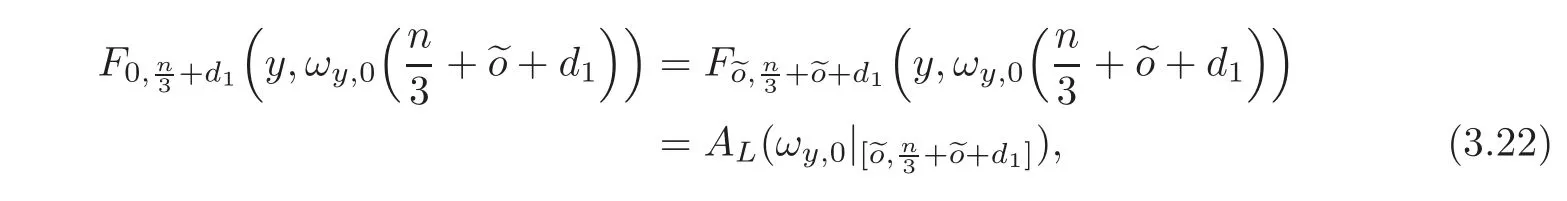
where the last equality holds since ωy,0is a minimizing curve.Let η1:[0,+d1]→ M with η1(0)=y and η1(+d1)=p be a Tonelli minimizer.Then,in view of(3.21)–(3.22),we have

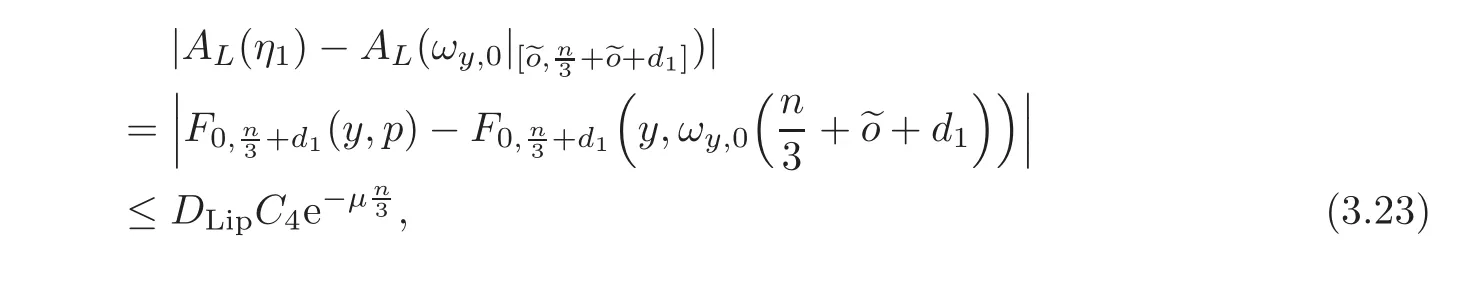
where DLip＞ 0 is a Lipschitz constant of Ft,t′ which is independent of t,t′with t+1 ≤ t′.

For the above sufficiently large n∈N with＞max{T1,2},let a(n)=−d1+τ.It is clear that a(n)≥and(dγp(−a(n)+ 〈τ〉),〈−a(n)+ 〈τ〉〉)=(p,vp,0).From(3.20)we have

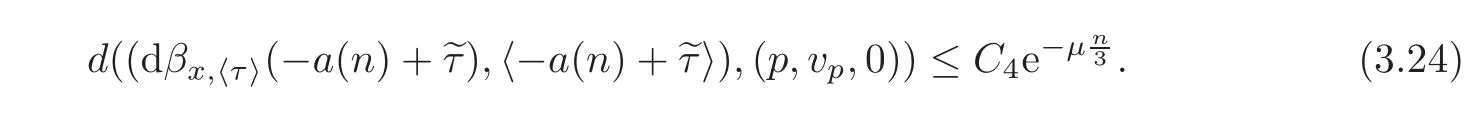
Since βx,〈τ〉is a minimizing curve,

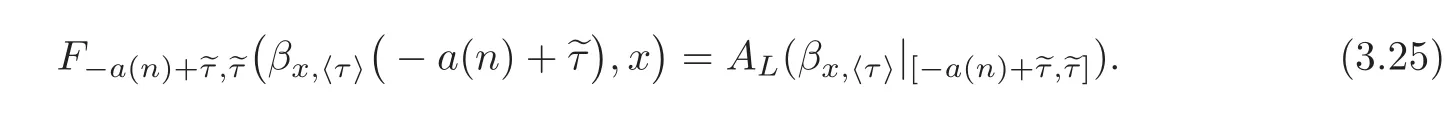
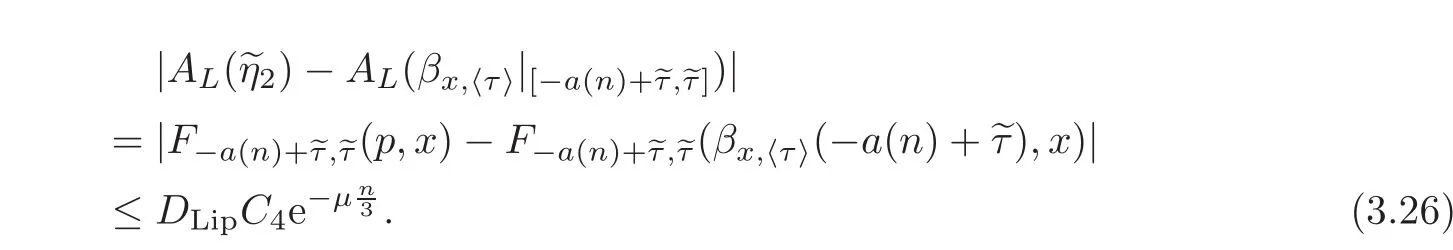
Define a curve η2:

Consider the curve η :[0,τ+n]→ M connecting y and x defined by

Now it remains to show that the curve defined by(3.27)is just the one we need.For n ∈ N large enough,from(3.15)we get

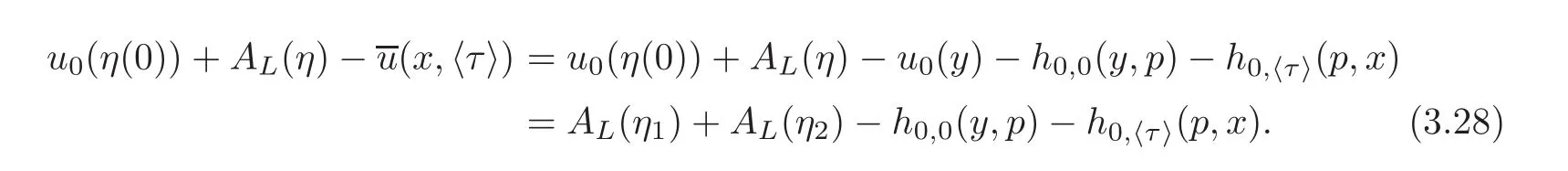
In view of(3.28),(3.23)and(3.26),we have

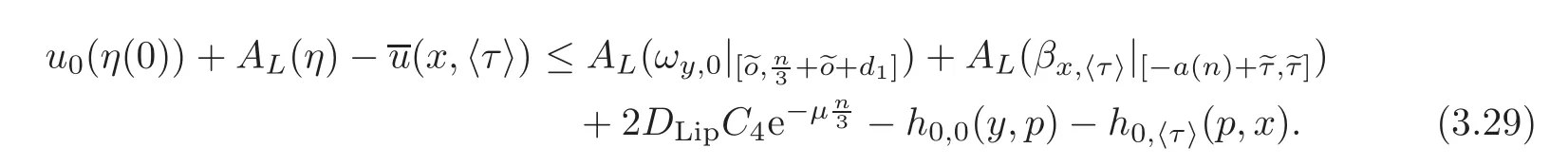
From(3.29)and(3.17)–(3.18),we have

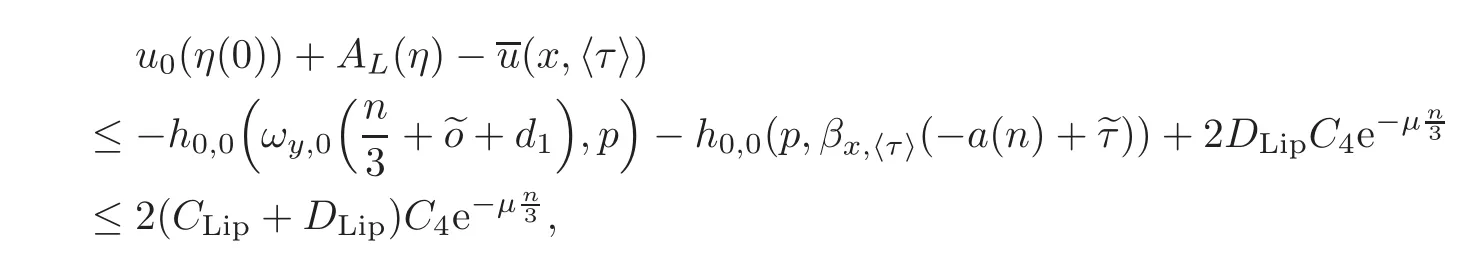
where the last inequality follows from h0,0(p,p)=0,(3.21)and(3.24).Let

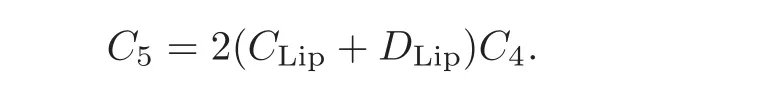
Note that C5andµare independent of(x,τ)∈M ×[0,1],u0∈C(M,R)and n∈N,which means that(3.16)holds.

Thus,for n∈N large enough,we have

Hence,there exists a constant C6＞0 such that

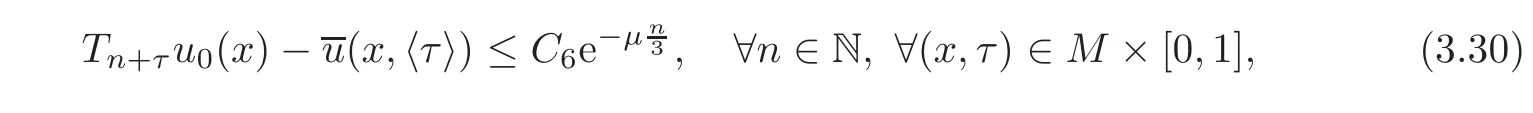
where the constant C6depends on u0.

The proof is now complete.

AcknowledgementsThe author would like to thank the referees for their helpful suggestions which help to make the paper more readable.

[1]Barreira,L.and Valls,C.,Hö lder Grobman-Hartman linearization,Discrete Contin.Dyn.Syst.,18,2007,187–197.

[2]Bernard,P.,Connecting orbits of time dependent Lagrangian systems,Ann.Inst.Fourier(Grenoble),52,2002,1533–1568.

[3]Contreras,G.,Iturriaga,R.and S´anchez-Morgado,H.,Weak solutions of the Hamilton-Jacobi equation for time periodic Lagrangians,preprint.

[4]Fathi,A.,Th´eor`eme KAM faible et th´eorie de Mather sur les syst`emes lagrangiens,C.R.Acad.Sci.Paris S´er.I Math.,324,1997,1043–1046.

[5]Fathi,A.,Solutions KAM faibles conjugu´ees et barri`eres de Peierls,C.R.Acad.Sci.Paris S´er.I Math.,325,1997,649–652.

[6]Fathi,A.,Orbites h´et´eroclines et ensemble de Peierls,C.R.Acad.Sci.Paris S´er.I Math.,326,1998,1213–1216.

[7]Fathi,A.,Sur la convergence du semi-groupe de Lax-Oleinik,C.R.Acad.Sci.Paris S´er.I Math.,327,1998,267–270.

[8]Iturriaga,R.and S´anchez-Morgado,H.,Hyperbolicity and exponential convergence of the Lax-Oleinik semigroup,J.Differential Equations,246,2009,1744–1753.

[9]Lions,P.,Generalized Solutions of Hamilton-Jacobi Equations,Research Notes in Mathematics,Pitman Publishing,London,1982.

[10]Ma˜n´e,R.,On the minimizing measures of Lagrangian dynamical systems,Nonlinearity,5,1992,623–638.

[11]Ma˜n´e,R.,Generic properties and problems of minimizing measures of Lagrangian systems,Nonlinearity,9,1996,273–310.

[12]Ma˜n´e,R.,Lagrangianflows:The dynamics of globally minimizing orbits,Bol.Soc.Brasil.Mat.,28,1997,141–153.

[13]Mather,J.,Action minimizing invariant measures for positive definite Lagrangian systems,Math.Z.,207,1991,169–207.

[14]Mather,J.,Variational construction of connecting orbits,Ann.Inst.Fourier(Grenoble),43,1993,1349–1386.

[15]S´anchez-Morgado,H.,Hyperbolicity and exponential long-time convergence for space-time periodic Hamilton-Jacobi equations,Proc.Amer.Math.Soc.,143,2015,731–740.

[16]Wang,K.and Yan,J.,The rate of convergence of the Lax-Oleinik semigroup-degeneratefixed point case,Sci.China Math.,54,2011,545–554.

[17]Wang,K.and Yan,J.,A new kind of Lax-Oleinik type operator with parameters for time-periodic positive definite Lagrangian systems,Commun.Math.Phys.,309,2012,663–691.

[18]Wang,K.and Yan,J.,The rate of convergence of the new Lax-Oleinik type operator for time-periodic positive definite Lagrangian systems,Nonlinearity,25,2012,2039–2057.