Homological Epimorphisms,Compactly Generated t-Structures and Gorenstein-Projective Modules

Nan GAO Xiaojing XU

1 Introduction

The concepts of recollements of triangulated categories and a t-structure on a triangulated category were introduced by Beilinson,Bernstein and Deligne[7].To build the category of perverse sheaves,they provided a way of gluing t-structures with respect to recollements of triangulated categories.Such a gluing procedure is called the BBD-induction for simplicity.This subject has been developed thoroughly.See for examples[1–3,9,11,18,21–22,24–25].

Recently,Broomhead,Pauksztello and Ploog[9]studied how to generate a new t-structure for a given finite set of t-structures on a triangulated category.They showed that given afinite set of compactly generated t-structures in a triangulated category with set-indexed coproducts,the extension closure of aisles is also an aisle.We call this new t-structure the BPP-induction for simplicity.Given a recollement(Y,D,X)of triangulated categories and twofinite sets S1and S2of compactly generated t-structures with the same index on X and Y.Then by taking a compactly generated t-structure in S1and a compactly generated t-structure of the same index in S2,we get afinite set S of their BBD-inductions.Qin and Gao[20]showed that if each object in S is compactly generated,then the BPP-induction of objects in S is exactly the BBD-induction of the BPP-induction of objects in S1and the BPP-induction of objects in S2.

Given a recollement(T′,T,T′′,i∗,i∗,i!,j!,j∗,j∗)of triangulated categories with small coproducts,thefirst part of our work is to show that the BBD-induction of compactly generated t-structures is compactly generated,if T is compactly generated and i∗preserves compact objects.Then we generalize this to the case of a ladder of height 2 and apply it to the ladder induced by homological ring epimorphisms.Ourfirst main result is Theorem 2.1.

Gorenstein-projective modules introduced by Enochs and Jenda[14]play a fundamental role in Gorenstein homological algebra.It is well-known that the stable category offinitely generated Gorenstein-projective modules is a triangulated category,see for example[13].

Given a recollement of unbounded derived categories of algebras,a natural question arises:When it can induce a recollement of stable categories offinitely generated Gorenstein-projective modules over corresponding algebras.The last part of our paper is to show that one case does work,that is,it works if this recollement is induced by some homological ring epimorphism.Our second main result is Theorem 3.1.

2 The Compact Generation of BBD-Inductions

The goal of this section is to show that the BBD-induction of compactly generated tstructures is compactly generated for a recollement of derived categories induced by some homological ring epimorphism.

Let us begin by recalling some definitions and key lemmas for the proof of our first main theorem.

Recall from[7]that a t-structure on a triangulated category D is a pair(D′,D′′)of full subcategories satisfying

(1)D′[1]⊆ D′and D′′[−1]⊆ D′′;

(2)HomD(X,Y)=0 for all X ∈ D′and Y ∈ D′′[−1];

(3)for each Z in D there is a distinguished triangle X→Z→Y→X[1]with X∈D′and Y ∈ D′′[−1].

Let D be a triangulated category with set-indexed coproducts and S a set of compact objects of D.Denote by Susp(S)the smallest full subcategory of D containing S closed under suspension,extensions,set-indexed coproducts and direct summands.Put D′:=Susp(S)and D′′:={Y ∈D|HomD(X,Y[n])=0,for all X ∈S and n≤0}.

Lemma 2.1(see[1,Theorem A.1])The pair(D′,D′′)is at-structure onD,which is called a compactly generatedt-structure.

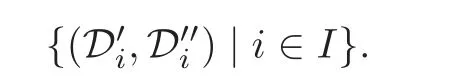
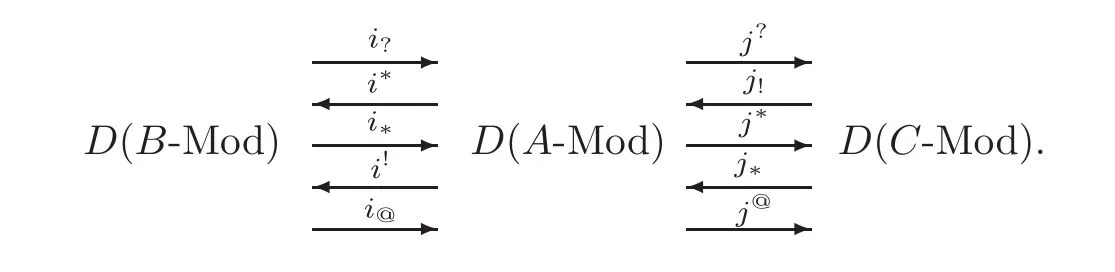
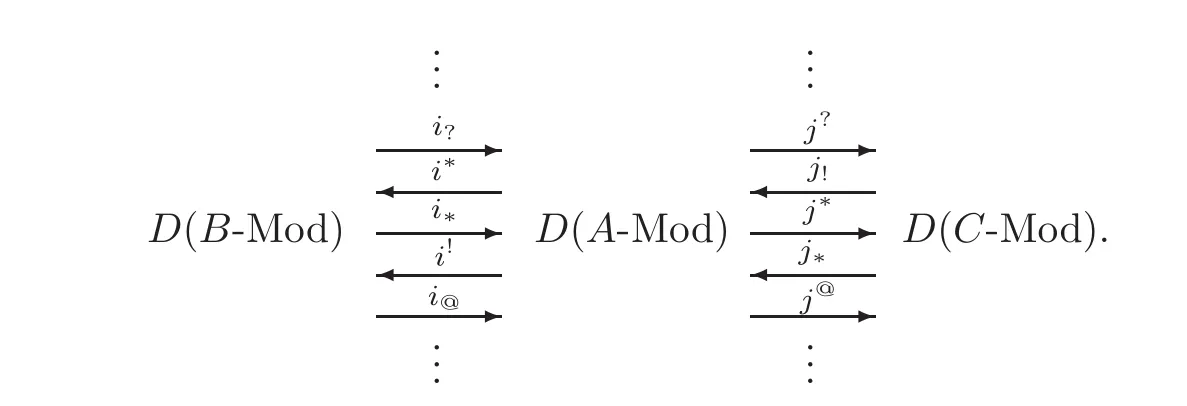
Let Y, D and X be triangulated categories. Recall from [7] that D is a recollement withrespect to Y and X, if there is a diagram of six triangle functors

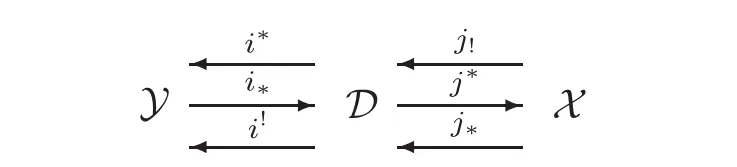
such that

where ∈Zis the counit of(j!,j∗),ηZis the unit of(i∗,i∗),ωZis the counit of(i∗,i!)and ζZis the unit of(j∗,j∗).

For short,we denote this recollement by(Y,D,X,i∗,i∗,i!,j!,j∗,j∗),or by(Y,D,X).Recall from[8],[27]or[22]that D is an upper recollement with respect to Y and X,if there is a diagram of four triangle functors

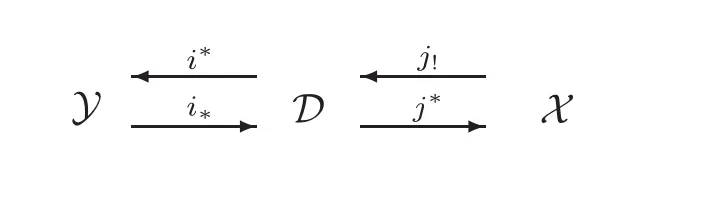
such that

where ∈Zis the counit of(j!,j∗)and ηZis the unit of(i∗,i∗).

Lemma 2.3(see[7,Theorem 1.4.10])Let(Y,D,X)be a recollement of triangulated categories.Suppose that(X′,X′′)and(Y′,Y′′)aret-structures onXandYrespectively.Then(D′,D′′)given by

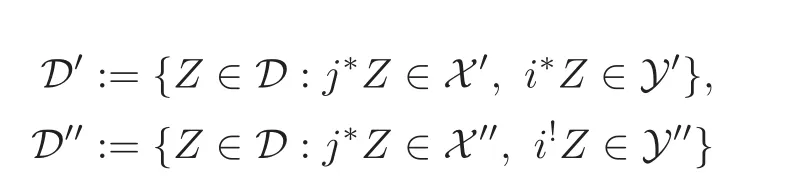
is at-structure onD,which is called the BBD-induction of(X′,X′′)and(Y′,Y′′)in[25].

Proposition 2.1Suppose that there exists the following recollement of triangulated categories:

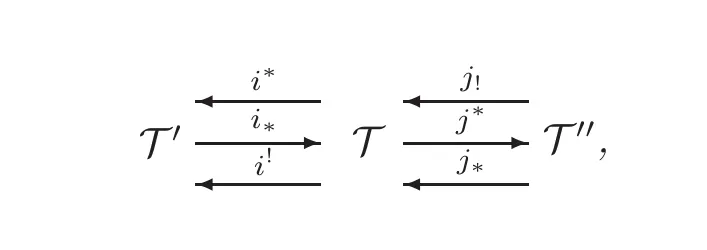
ProofSince T′,T,T′′admit small coproducts and T is compactly generated,it follows from[6]that i∗and j!preserve compact objects.Since i∗preserves compact objects,we obtain from[6]again that j∗preserves compact objects.Since(j!,j∗)is an adjoint pair,we get from[26,Theorems 4.1 and 5.1]that j!and j∗preserve small coproducts.Since(i∗,i∗)is an adjoint pair and i∗preserves compact objects,we get from[26,Theorems 4.1 and 5.1]that i∗and i∗preserve small coproducts.

(1) Let(X′,X′′)and(Y′,Y′′)be two compactly generated t-structures on T′′and T′respectively,and(D′,D′′)be the BBD-induction.Then by the definition there is a set S1of compact objects of T′′such that X′=Susp(S1)and a set S2of compact objects of T′such that Y′=Susp(S2).Since i∗and j!preserve compact objects,we get that j!S1∪ i∗S2is a set of compact objects of T.

We claim that D′=Susp(j!S1∪ i∗S2).Indeed,let Z be an object in D′.Then by the definition j∗Z ∈ X′=Susp(S1)and i∗Z ∈ Y′=Susp(S2).Consider the distinguished triangle j!j∗Z → Z → i∗i∗Z → (j!j∗Z)[1].Since the triangle functors j!and i∗preserve coproducts and direct summands,it follows that j!j∗Z ∈ Susp(j!S1)and i∗i∗Z ∈ Susp(i∗S2).So Z ∈Susp(j!S1∪ i∗S2),this means that D′⊆ Susp(j!S1∪ i∗S2).On the other hand,let X be an object in S1.Then j∗j!XX ∈ Susp(S1)=X′and i∗j!X=0 ∈ Y′.So j!X ∈ D′.Let Y be an object in S2.Then j∗i∗Y=0 ∈ X′and i∗i∗YY ∈ Susp(S2)=Y′.So i∗Y ∈ D′.It follows that j!S1∪ i∗S2⊆ D′.Since(i∗,i!)is an adjoint pair and i∗preserves small coproducts,we get from[26,Theorem 5.1]that i!preserves coproducts.Since j∗and i∗preserve coproducts,we have Susp(j!S1∪ i∗S2) ⊆ D′.Thus D′=Susp(j!S1∪ i∗S2)and(D′,D′′)is a compactly generated t-structure.

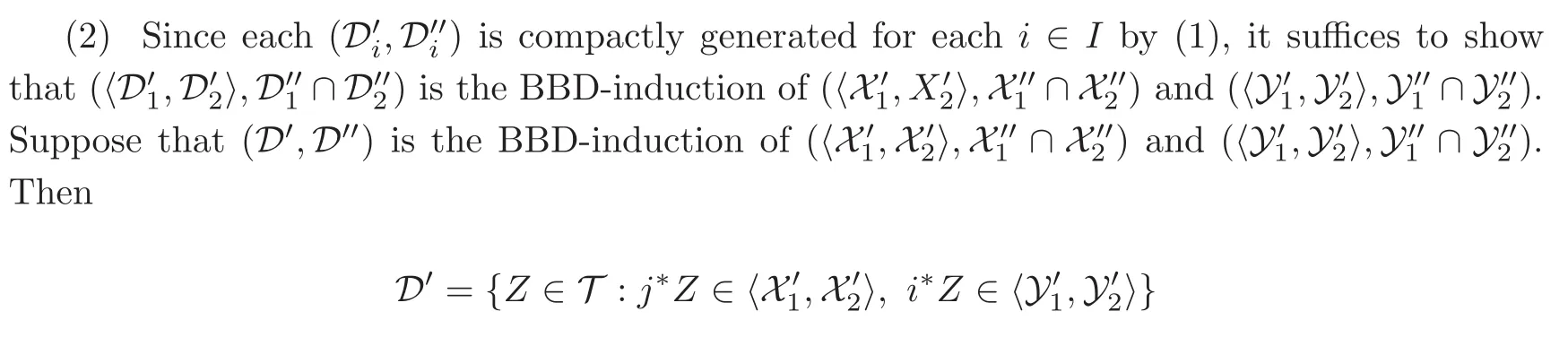
and

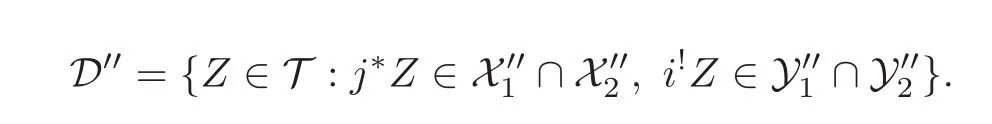
and

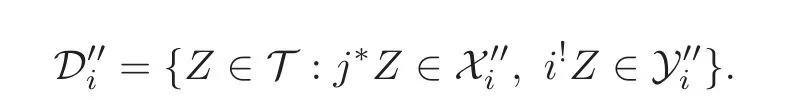
Let R and S be rings.Recall from[16]that a ring epimorphism λ :R → S is homological,if(S,S)=0 for all j＞0.This is equivalent to that the restriction functor D(λ∗):D(S-Mod)→ D(R-Mod)is fully faithful,where D(S-Mod)(resp.D(R-Mod))denotes the unbounded derived category of modules category over S(resp.R).We denote by pdRS the projective dimension of S as a left R-module.Denote by D(R-Mod)cthe triangulated subcategory of compact objects in D(R-Mod).

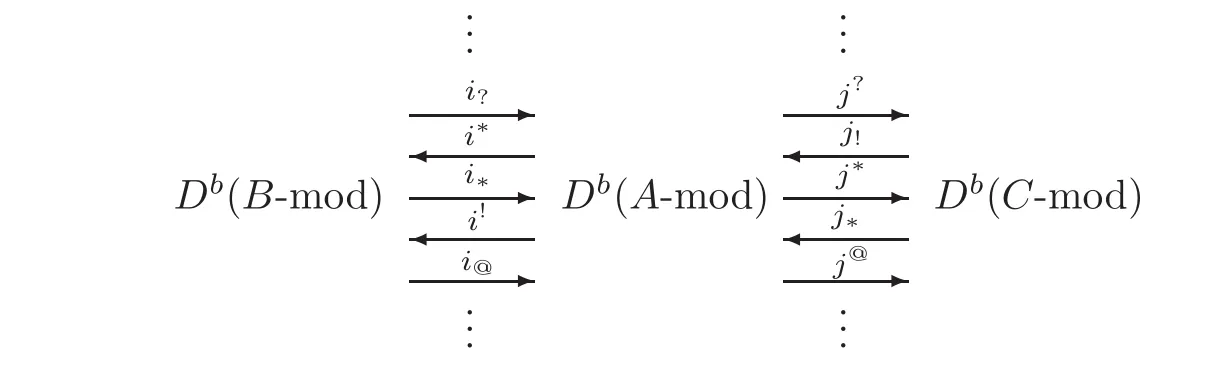
Corollary 2.1LetAandBbe projectivek-algebras over a commutative ringk.Letλ:A→Bbe a homological ring epimorphism which induces a recollement of unbounded derived categories

ProofNote that D(A-Mod),D(B-Mod)and D(C-Mod)admit small coproducts and are compactly generated.We denote by D(A-Mod)cthe full subcategory of compact objects in D(A-Mod),similarly for D(B-Mod)c.Since D(A-Mod)c=Kb(A-proj),D(B-Mod)c=Kb(B-proj)and pdAB＜∞,it follows thatAB is a compact object in D(A-mod).This implies that i∗preserves compact objects.Thus by Proposition 2.1 we complete the proof.

Definition 2.1(see[4,Section 3;8,Section 1.5])A ladderLis afinite or infinite diagram of triangulated categories and triangle functors

such that any three consecutive rows form a recollement.The rows are labelled by a subset ofZand multiple occurence of the same recollment is allowed.The height of a ladder is the number of recollements contained in it(counted with multiplicities).

Theorem 2.1Suppose that there is a ladder of triangulated categories of height2

whereT′,T,T′′admit small coproducts andTis compactly generated.Let(X′,X′′)and(Y′,Y′′)be twofinite sets of compactly generatedt-structure onT′′andT′respectively.Let()be their BBD-induction corresponding to the recollement(T′,T,T′′).Then()is a compactly generatedt-structure.

ProofBy assumption(T′′,T,T′,j∗,j∗,j?,i∗,i!,i?)is a recollement.Since T′′,T,T′admit small coproducts and T is compactly generated,it follows from[6]that i∗preserves compact objects.By Proposition 2.1,we immediately get thatis a compactly generated tstructure.

For short,we denote this ladder by(T′,T,T′′,i∗,i∗,i!,i?,j!,j∗,j∗,j?),or by(T′,T,T′′,T,T′).

Corollary 2.2LetA,BandCbe projectivek-algebras over a commutative ringk.Letλ1:A → Bandλ2:A → Cbe two homological ring epimorphisms which induce a ladder of height2

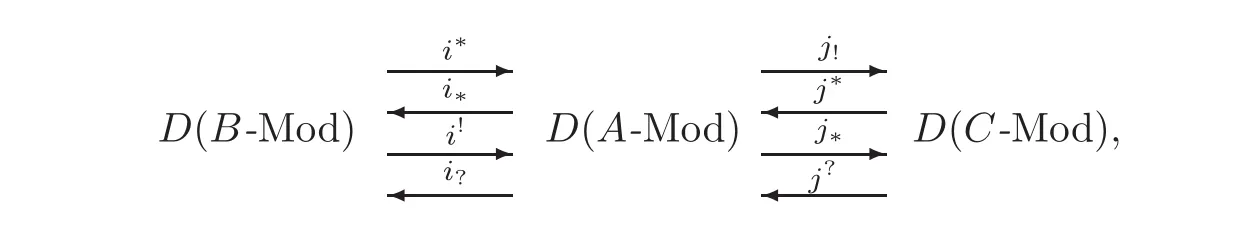
wherei!andj∗are the restriction functors induced byλ1andλ2,respectively.Let(X′,X′′)be a compactly generatedt-structure onD(C-Mod)and(Y′,Y′′)a compactly generatedtstructure onD(B-Mod).Letbe their BBD-induction corresponding to the recollement(D(B-Mod),D(A-Mod),D(C-Mod)).Thenis a compactly generatedt-structure.

ProofNote that D(A-Mod),D(B-Mod)and D(C-Mod)admit small coproducts and D(A-Mod)is compactly generated.Thus by Theorem 2.1 we obtain the desired result.

Example 2.1Let A=be an upper triangular matrix algebra,where B,C arefinite dimensional k-algebras over a field k and M is a finite dimensional C-B-bimodule.Let(X′,X′′)be a compactly generated t-structure on D(C-Mod)and(Y′,Y′′)a compactly generated tstructure on D(B-Mod).Then

(1)there is a ladder of height 2

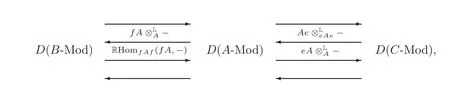
(2)the BBD-induction of(X′,X′′)and(Y′,Y′′)corresponding to the recollement(D(B-Mod),D(A-Mod),D(C-Mod))is a compactly generated t-structure.

ProofLet e=Then A/AeA=B=fA=fAf,A/AfA=C=Ae=eAe,eAf=M and fAe=0.It follows that AeA is a projective right A-module and AfA is a projective left A-module,and so by[23,Remark 3.2]AeA and AfA are stratifying ideals of A.Furthermore,λ1:A → B and λ2:A → C are homological ring epimorphisms and they induce a ladder of height 2

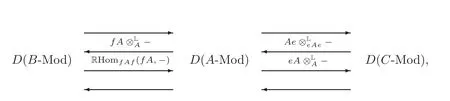
where RHomfAf(fA,−)and Ae− are the restriction functors induced by λ1and λ2.By Corollary 2.2 we complete the proof.

Remark 2.1We mention that(1)in Example 2.1 is implicit in[4,Example 3.4].

3 Recollements of Gorenstein Projective Modules

The goal of this section is to show that a recollement of derived categories of algebras induced by some homological ring epimorphism produces a ladder of the stable categories of Gorenstein-projective modules over corresponding algebras.

Before we state our last main theorem,we fix some notation and recall some definitions and facts.

Throughout this section,let A be a finite dimensional k-algebra over a field k and A-Mod the category of left A-modules.Denote by A-mod the full subcategory offinitely generated left A-modules,by A-proj the full subcategory of projective A-modules in A-mod,and by pdAX the projective dimension of X in A-mod.Recall that an A-module M in A-mod is said to be Gorenstein-projective,if there is an exact sequence P·= ···→ P−1→ P0d0→ P1→ P2→ ···in A-proj with HomA(P·,Q)exact for any A-module Q in A-proj,such that M=kerd0(see[14,Definition 10.2.1]).Denote by A-Gproj the full subcategory of Gorenstein-projective modules in A-mod.

Denote by Kb(A-proj)the bounded homotopy category of A-proj,by D(A-Mod)the unbounded derived category of A-Mod,and by Db(A-mod)the bounded derived category of A-mod.Denote by Dsg(A)the singularity category of A,which is defined as the Verdier quotient category of Db(A-mod)with respect to the thick subcategory Kb(A-proj).

Theorem 3.1LetAbe a Gorenstein algebra.Letλ :A → Bbe a homological ring epimorphism which induces a recollement of derived categories of algebrasB,AandC

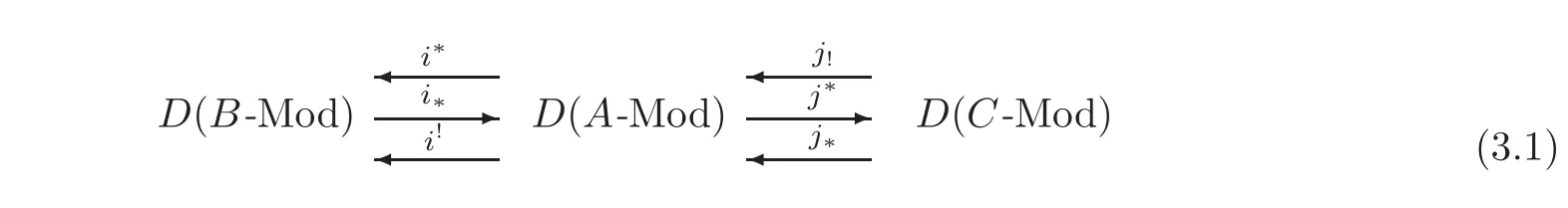
such thatj!restricts toDb(C-mod).IfpdAB＜∞,then there is an unbounded ladder

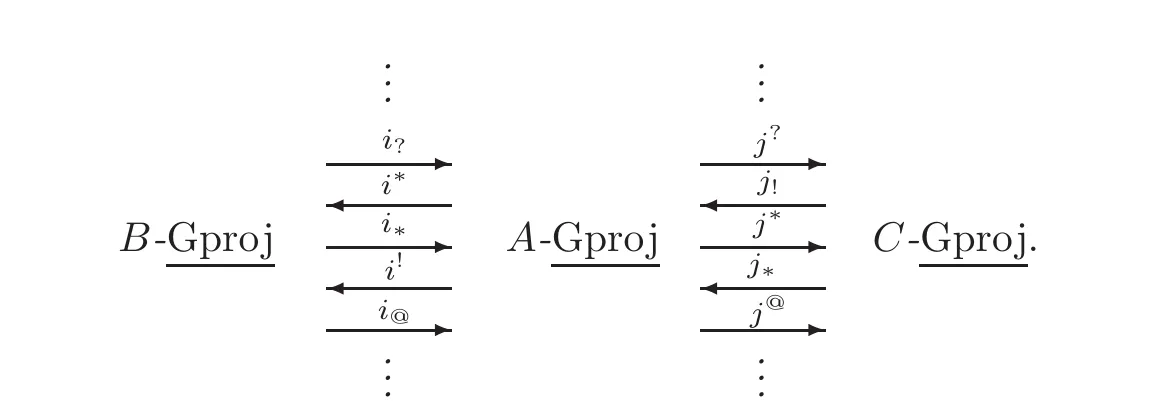
ProofSince λ :A → B is a homological ring epimorphism,it follows from[2,1.6 and 1.7]that i∗=AB−.Since pdAB ＜ ∞,it follows that i∗(B)∈ Kb(A-proj).Since D(A-Mod),D(B-Mod)and D(C-Mod)admit small coproducts and are compactly generated,and also D(A-Mod)c=Kb(A-proj),D(B-Mod)c=Kb(B-proj)and D(C-Mod)c=Kb(C-proj),we obtain from[6]that j∗and i∗restrict to Kb(A-proj),and j!restricts to Kb(C-proj).This implies from[26,Theorems 4.1 and 5.1]that j∗has a right adjoint.Since j!restricts to Db(C-mod)and i∗(B) ∈ Kb(A-proj),we get from[4,Theorem 4.6]that(3.1)restricts to a recollement

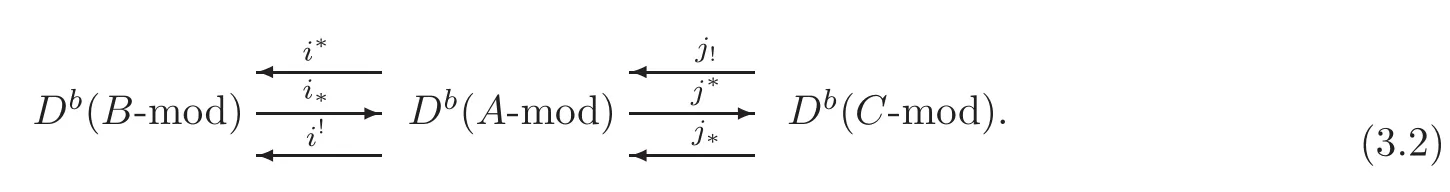
Since A is Gorenstein,it follows from[27,Theorem 3.1]and(3.2)that B and C are Gorenstein.Since j!restricts to Db(C-mod),it follows from[4,Proposition 3.2]that j!admits a left adjoint.Thus there exists a ladder of height 3

Moreover,i?restricts to Kb(B-proj)and j?restricts to Kb(A-proj).

Since i∗restricts to Kb(A-proj),it follows from[19,Lemma 1]that i?restricts to Db(B-mod).This means from[4,Proposition 3.2]that i?admits a left adjoint. Since i∗restricts to Db(B-mod),we get from[19,Lemma 1]again that i!restricts to Kb(A-proj).So we know from[26,Theorems 4.1 and 5.1]that i@has a right adjoint.We proceed the same procedure.Then there exists the following unbounded ladder

Furthermore,we also obtain from above arguments that there are the following two induced unbounded ladders:

and

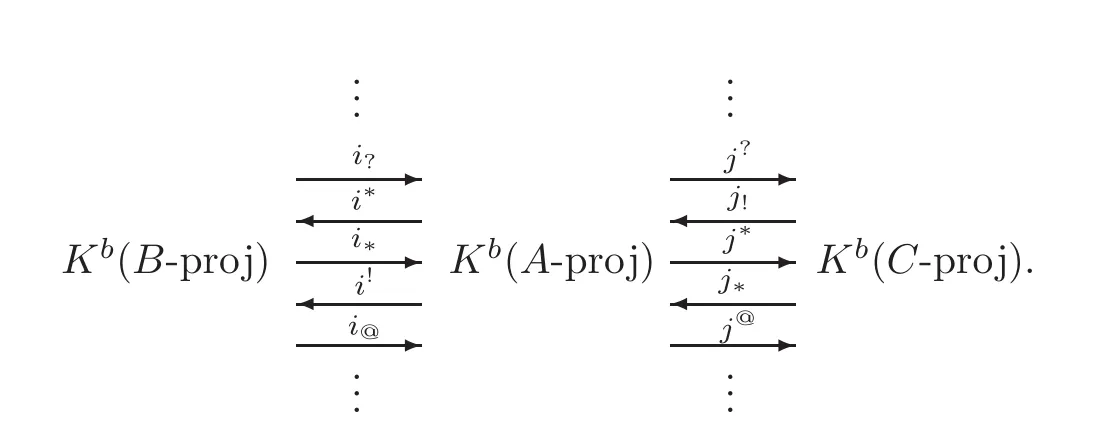
Thus we get an unbounded ladder of singularity categories

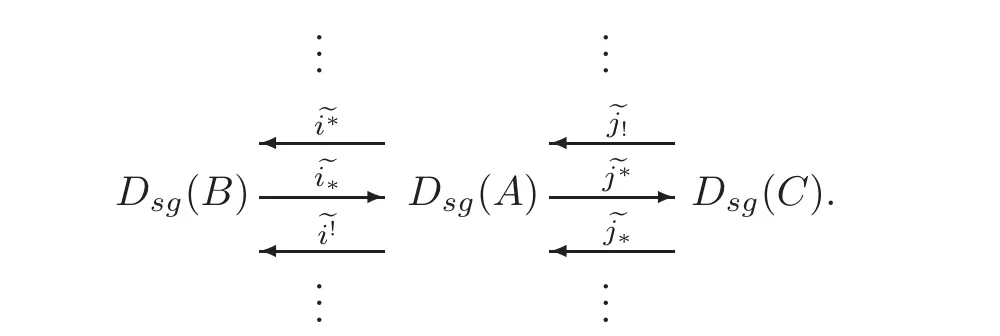
Since A,B and C are Gorenstein,it follows from[10]that there are triangle-equivalencesThis implies the desired ladder.

Before stating the following corollary,we recall the notion of stratifying ideals.Let A be an algebra and e an idempotent of A.The two-sided ideal AeA generated by e is called a stratifying ideal if the multiplication map Ae⊗eAeeA→AeA is bijective and ToreAen(Ae,eA)=0 for all n＞0,or equivalently,the canonical epimorphism λ:A→A/AeA is homological(see[12]).

Corollary 3.1LetAbe a Gorenstein algebra.Letebe an idempotent ofAsuch thatAeAis a stratifying ideal withpdAAeA＜∞andeAehasfinite global dimension.Then there is a

ProofSince AeA is a stratifying ideal,there is from[12,Section 2]the following recollement

Since A is a finite dimensional algebra and the global dimension of eAe isfinite,we get that Ae−restricts to Db(eAe-mod)and eAe-Gproj=eAe-proj.Since pdAAeA＜ ∞,it follows that pdAA/AeA＜∞.Thus by Theorem 3.1 there exists an unbounded ladder

This implies that there is a triangle-equivalence

Let A and B be two rings,ANBan A-B-bimodule,andBMAa B-A-bimodule.Assume that ϕ:M⊗AN →B is a B-B-bimodule homomorphism and ψ:N⊗BM →A is an A-A-bimodule homomorphism,such that ϕ(m ⊗ n)m′=mψ(n⊗m′)and nϕ(m ⊗ n′)= ψ(n⊗m)n′for all m,m′∈ M and n,n′∈ N.Following[5],the Morita ring is defined as follows:

where the addition of elements of Λ(ϕ,ψ)is componentwise and the multiplication is given by

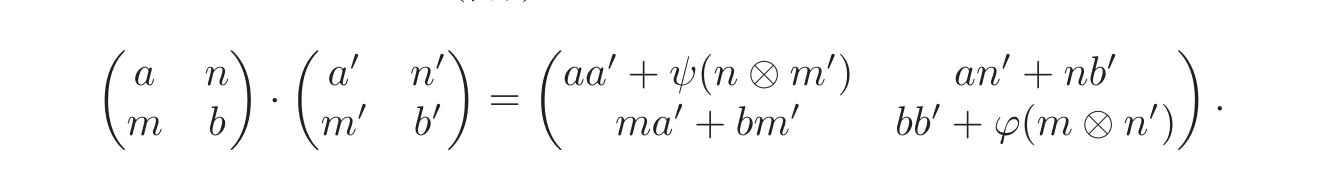
Note that Λ(ϕ,ψ)is an associative ring.Then we have the following example.

Example 3.1Let A be a Gorenstein algebra,and let e and f be two idempotent elements of A such that fAe=0.Let N:=Ae⊗kfA and Λ(0,0):=.Then there exists an unbounded ladder

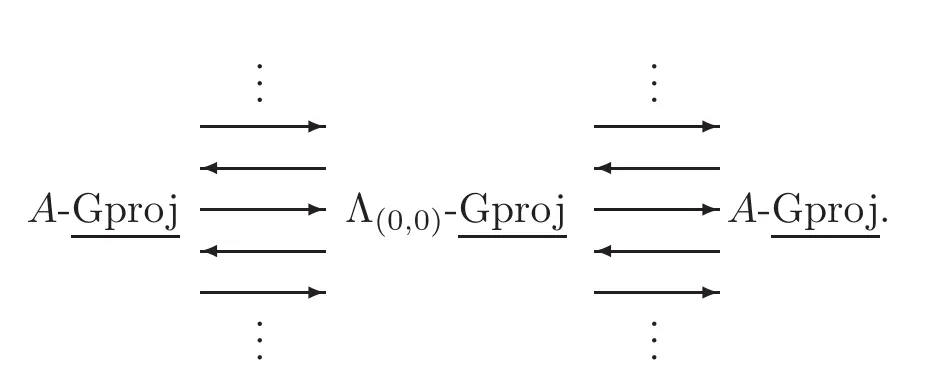
ProofSince fAe=0,it follows that N ⊗AN=0.This implies that Λ(0,0)is a Morita ring and furthermore there is the following recollement of module categories by[15,Proposition 2.4]or[17]

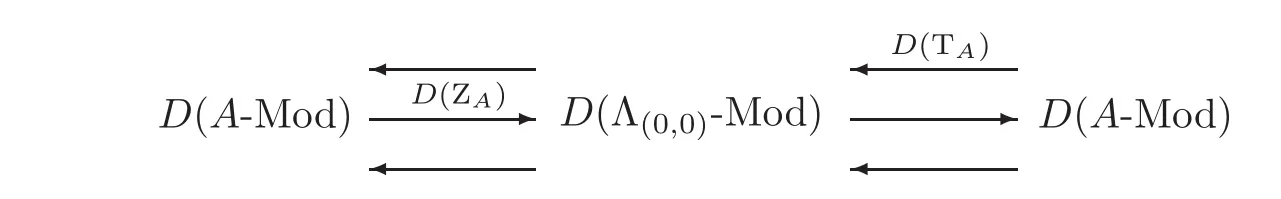
such that D(TA)restricts to Db(A-mod).Since A is Gorenstein,we obtain from[15,Corollary 4.15]that Λ(0,0)is Gorenstein.By Theorem 3.1 we complete the proof.

The following example is implicit in[29,Theorem 2.1].Now we explain it from another point of view for our purpose.

Example 3.2Let Λ=()be a Gorenstein algebra with pdAM ＜ ∞.Then there is an unbounded ladder

ProofLet e=with e+f=1Λ.Then A= Λ/ΛeΛ and B=eΛe.Since ΛeΛ = Λe is a projective left Λ-module,we get from[23,Remark 3.2]that ΛeΛ is a stratifying ideal of Λ.So there is an induced homological ring epimorphism λ :A → Λ.

Since A= Λ/ΛeΛ =fΛf= Λf,we know that A is a projective left Λ-module.Since Λ is Gorenstein and pdAM ＜ ∞,it follows from[28,Theorem 2.2]that pdMB＜ ∞.Byj!restricts to Db(B-mod).Thus by Theorem 3.1 we get the desired ladder.

AcknowledgementsSome of this work was done during a stay of the corresponding author at the University of Stuttgart.The corresponding author would like to express her gratitude to Professor Steffen Koenig for the warm hospitality.The authors are grateful to the referee for simplifying the proof of Theorem 2.1 and improving Theorem 3.1,and for many useful remarks and suggestions that improve significantly the exposition of the paper.

[1]Alonso Tarr´io,L.,Jerem´ias L´opez,A.and Souto Salorio,M.J.,Construction of t-structures and equivalences of derived categories,Trans.Amer.Math.Soc.,355,2003,2523–2543.

[2]Angeleri Hügel,L.,Kö nig,S.and Liu,Q.H.,Recollements and tilting objects,J.Pure Appl.Algebra,215,2011,420–438.

[3]Angeleri Hügel,L.,Kö nig,S.and Liu,Q.H.,Jordan-Hö lder theorems for derived module categories of piecewise hereditary algebras,J.Algebra,352,2012,361–381.

[4]Angeleri Hügel,L.,Kö nig,S.,Liu,Q.H.and Yang,D.,Ladders and simplicity of derived module categories,2015,arXiv:1310.3479v2.

[5]Bass,H.,The Morita Theorems,Mimeographed Notes,University of Oregon,Eugene,1962.

[6]Beligiannis,A.and Reiten,I.,Homological and Homotopical Aspects of Torsion Theories,Mem.Amer.Math.Soc.,188(883),Amer.Math.Soc.,Providence,2007.

[7]Beilinson,A.,Bernstein,J.and Deligne,P.,Faisceaux pervers,Analysis and Topology on Singular Spaces,Luminy 1981,Ast´erisque,100,Soc.Math.France,Paris,1982.

[8]Beilinson,A.,Ginsburg,V.and Schechtman,V.,Koszul duality,J.Geom.Phys.,5(3),1998,317–350.

[9]Broomhead,N.,Pauksztello,D.and Ploog,D.,Averaging t-structures and extension closure of aisles,J.Algebra,394,2013,51–78.

[10]Buchweitz,R.O.,Maximal Cohen-Macaulay modules and Tate-Cohomology over Gorenstein rings,Unpublished manuscript,1987.

[11]Chen,H.X.and Xi,C.C.,Good tilting modules and recollements of derived module categories,Proc.Lond.Math.Soc.,104(5),2012,959–996.

[12]Cline,E.,Parshall,B.and Scott,L.,Stratifying endomorphism algebras,Mem.Amer.Math.Soc.,124(591),1996,1993–1999.

[13]Chen,X.W.,Relative singularity categories and Gorenstein-projective modules,Math.Nachr.,284(2–3),2011,199–212.

[14]Enochs,E.E.and Jenda,O.M.G.,Relative Homological Algebra,de Gruyter Exp.Math.,30,Walter de Gruyter Co.,Berlin,2000.

[15]Gao,N.and Psaroudakis,C.,Gorenstein homological aspects of monomorphism Categories via Morita Rings,2015,arXiv:1508.02843.

[16]Geigle,W.and Lenzing,H.,Perpendicular categories with applications to representation and sheave,J.Algebra,144(2),1991,273–343.

[17]Green,E.L.and Psaroudakis,C.,On Artin algebras arising from Morita contexts,Algebr.Represent.Theory,17(5),2014,1485–1525.

[18]Han,Y.,Recollement and Hochschild theory,J.Algebra,197,2014,535–547.

[19]Han,Y.and Qin,Y.Y.,Reducing homological conjectures by n-recollements,Algebr.Represent.Theory,19(2),2016,377–395.

[20]Hao,K.Q.and Gao,N.,The extension closure of gluing t-structures(in Chinese),Commun.Appl.Math.Comput.,30(3),2016,364–368.

[21]Keller,B.and Vossieck,D.,Aisles in derived categories,Bull.Soc.Math.Belg.,40,1998,239–253.

[22]Kö nig,S.,Tilting complexes,perpendicular categories and recollements of derived module categories of rings,J.Pure Appl.Algebra,73(3),1991,211–232.

[23]Kö nig,S.and Nagase,H.,Hochschild cohomology and stratifying ideals,J.Pure Appl.Algebra,213,2009,886–891.

[24]Kö nig,S.and Yang,D.,Silting objects,simple-minded collections,t-structures and co-t-structures forfinite-dimensional algebras,Doc.Math.,19,2014,403–438.

[25]Liu,Q.H.,Vitoria,J.and Yang,D.,Gluing silting objects,Nagoya Math.J.,216,2014,117–151.

[26]Neeman,A.,The Grothendieck duality theorem via Bousfields techniques and Brown representability,J.Amer.Math.Soc.,9(1),1996,205–236.

[27]Pan,S.Y.,Recollements and Gorenstein algebras,Int.J.Algebra,7(17–20),2013,829–832.

[28]Xiong,B.L.and Zhang,P.,Gorenstein-projective modules over triangular matrix Artin algebras,J.Algebra Appl.,11(4),2012,14,1802–1812.

[29]Zhang,P.,Zhang,Y.H.,Zhou,G.D.and Zhu,L.,Unbounded ladders induced by Gorenstein algebras,2016,arXiv:1507.07333v3.