On a Vector Version of a Fundamental Lemma of J.L.Lions∗

Philippe G.CIARLETMaria MALINCristinel MARDARE

1 Introduction

All notations and definitions are not explained here,see Section 2.

Given any open subset Ω of RN,the implication

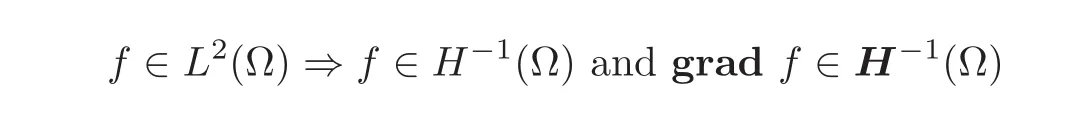
clearly holds.While the converse implication,viz.,

does not necessarily hold in general(see,e.g.,the counterexample of Geymonat and Gilardy[11]),it does if Ω is a domain in RN,i.e.,a bounded and connected open subset of RNwith a Lipschitz-continuous boundary,the set Ω being locally on the same side of its boundary(for details about domains,see Adams[1]or Neˇcas[22]).

This fundamental observation is due to J.L.Lions(see the footnote 27 in Magenes and Stampacchia[19]).Itsfirst published proofs appeared in Theorem 3.2 in Chapter 3 of Duvaut and Lions[10]and in Tartar[23],for domains with sufficiently smooth boundaries.It was later shown by Geymonat and Suquet[14]that this implication holds in fact if Ω is any domain in RN,i.e.,with a boundary that is only Lipschitz-continuous.

This result was further generalized by Borchers and Sohr[6]and Amrouche and Girault[4],who showed that the assumption “f ∈ H−1(Ω)” can be replaced by the weaker assumption“f ∈ D′(Ω)” and that the spaces H−1(Ω),resp.L2(Ω),can be replaced with the more general spaces H−m(Ω),resp.H−m+1(Ω),where m is now any integer≥ 1,according to the following result.

Theorem 1.1(J.L.Lions Lemma)LetΩbe a domain inRNand letm ≥ 1be an integer.Then the following implication holds:

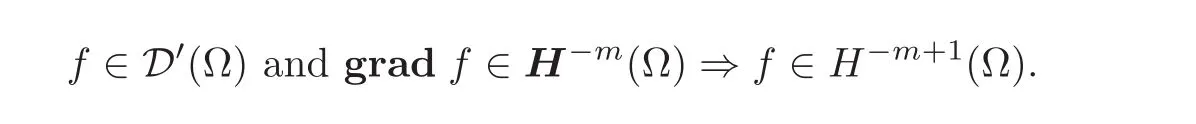
Note that it was also shown in[4,6]that,more generally,

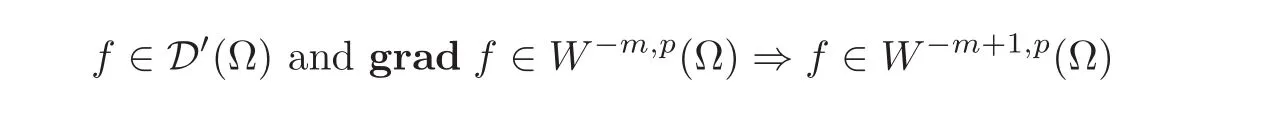
for any integer m≥1 and any p∈R such that p＞1.

J.L.Lions lemma was then generalized to vector-valued distributions,i.e.,in D′(Ω)(instead of“scalar” distributions in D′(Ω)),by Amrouche,Ciarlet,Gratie and Kesavan[3]according to the following result.

Theorem 1.2(Vector Version of J.L.Lions Lemma)LetΩbe a domain inRNand letm≥1be an integer.Then the following implication holds:

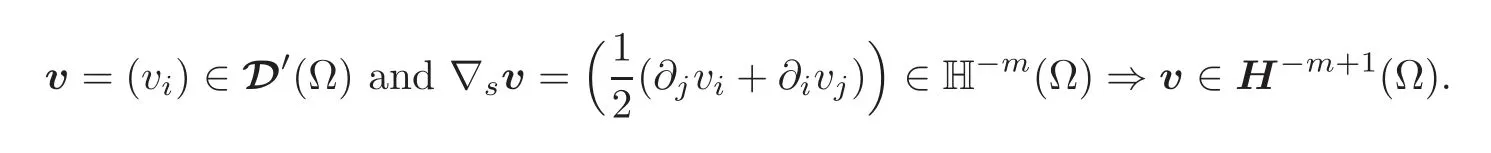
ProofLet v=(vi)∈ D′(Ω)be such thatwell-known identity

which holds here in the space H−m−1(Ω)⊂ D′(Ω),implies that∂kvi∈ H−m(Ω),which in turn implies that vi∈ H−m+1(Ω),thanks to two successive applications of J.L.Lions lemma(see Theorem 1.1).

Incidentally,Theorem 1.2 shows that the natural analog in the vector version of J.L.Lions lemma of the gradient operator grad of the scalar case is the symmetrized gradient operator∇s.

We shall be concerned in this paper with the special case m=1 of Theorem 1.2,viz.,with the implication

More specifically,our main objective is to show that this implication is in effect equivalent to a certain number of other fundamental properties(cf.Theorems 3.1,4.1–4.2),by means of natural“vector versions” of similar equivalences that were shown to hold in[2]in the scalar case.

2 Notations and Other Preliminaries

Throughout the article,an integer N ≥ 2 is given and,unless otherwise specified,Latin indices take their values in the set{1,2,···,N}.

All the functions,matrices,etc.,considered here are real.The notations KerA and ImA respectively designate the kernel and the image,also known as the range,of a linear operator A.If B is a subset of a vector space X and λ ∈ R,then λB:={λx ∈ X;x ∈ B}.

Let X be a normed vector space.Given any x∈X and any r＞0,the notation B(x;r)designates the open ball with center x and radius r;given x∈X and a subset B of X,the distance from x to B is defined as d(x,B):=inf{d(x;y);y ∈ B};a subset B of X is said to be starlike with respect to an open ball B(x;r)if,for every z∈B,the convex hull of the set{z}∪B(x;r)is contained in B.

The dual of a topological space X is denoted X′and the duality between X′and X is denotedX′〈·,·〉X;given a subspace Z of X,the polar set Z0of Z is defined by

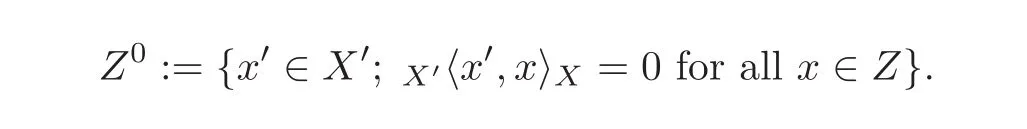
Given two normed vector spaces X and Y,the notation L(X;Y)designates the space of all continuous linear operators from X into Y,equipped with the operator norm.Given A ∈ L(X;Y),its dual is the operator A′∈ L(Y′;X′)defined byX′〈A′y′,x〉X=Y′〈y′,Ax〉Yfor all x ∈ X and all y′∈ Y′.

The notations(a)iand(A)ijrespectively designate the i-th component of a vector a∈RNand the components at the i-th row and j-th column of an N×N matrix A.The notation A=(aij)means that aij=(A)ij.The Kronecker’s symbol is denoted δij.The notation a ·b designates the Euclidean inner product of two vectors a∈RNand b∈RN.The set of all N×N symmetric,resp.antisymmetric,matrices is denoted SN,resp.AN.

In what follows,Ω denotes a non-empty open subset of RN,x=(xi)designates a generic point in Ω,and ∂i:=and ∂ij:= respectively designate the partial derivative operators of thefirst and second order,in the classical sense or in the sense of distributions.The notation ∂α,where α =is a multi-index,designates the partial differentialThe support of a function f:Ω → R is denoted suppf,and f|Adesignates the restriction of f to a subset A of Ω.

The notation D(Ω)designates the space of functions ϕ ∈ C∞(Ω)such that suppϕ is a compact subset of Ω.The space D(Ω)is equipped with its inductive limit topology(cf.,e.g.,Vo Khac[25]).Then a sequenceof functions ϕn∈ D(Ω)converges to a function ϕ ∈ D(Ω)in this topology if there exists a compact subset K of Ω such that

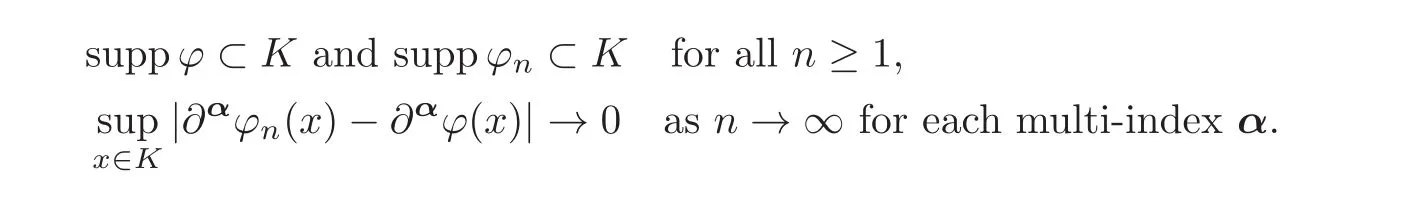
Such a convergence is denoted

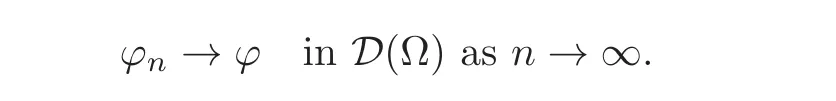
The notation D′(Ω)designates the dual space of D(Ω),i.e.,the space of distributions on Ω.The notations Hm(Ω)for each integer m ≥ 0,with H0(Ω):=L2(Ω),and the notations(Ω)and H−m(Ω)for each integer m ≥ 1,designate the usual Sobolev spaces and their duals.

Spaces of functions or distributions,vectorfields,and symmetric matrix fields,i.e.,with values in SN,are respectively denoted by italic capitals,boldface capitals,and special Roman capitals.For instance,

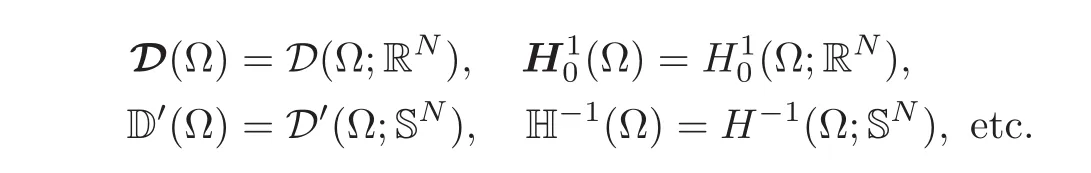
Such spaces are equipped with their natural product norms.For instance,

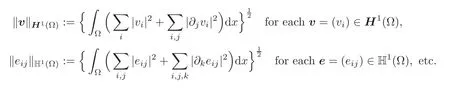
The following differential operators will be used in the sequel:

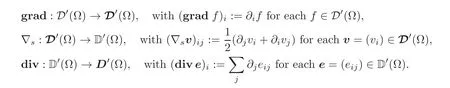
Note that,when Ω is connected,the kernel of the symmetrized gradient operator ∇shas a well-known characterization,viz.,

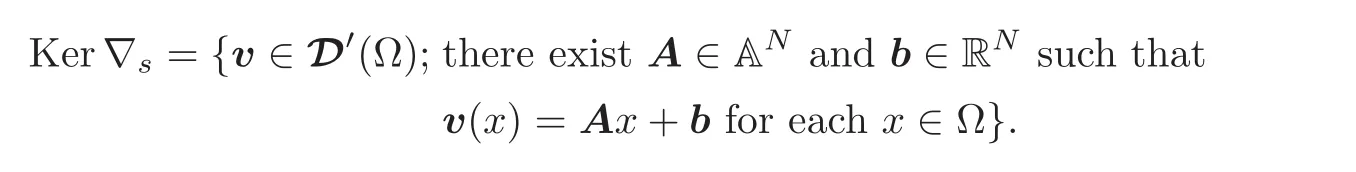
3 An Equivalence Theorem

We now show that the vector version of J.L.Lions lemma of Theorem 1.2 with m=1 is equivalent to a certain number of other properties,respectively noted(a),(b),(c),(d),(e),(f),and(g),in the next theorem.

In addition to their interest per se,some of these properties have interesting interpretations.

For instance,property(b)constitutes a “weak” vector version of J.L.Lions lemma,which is nothing but the natural vector version of the “original” lemma of J.L.Lions.

Property(c)constitutes a natural vector version of a well-known inequality due to Neˇcas in the “scalar” case(see[21–22],or Bramble[7]for a different proof).

Property(e)constitutes a weak version of the classical Donati compatibility conditions;see[3,12–13],where such conditions were used to define and analyze an intrinsic approach to linearized elasticity(a quick introduction to Donati compatibility conditions is found in Subsection 6.18 of[8]).These conditions are said here to be “weak” to reflect that the given matrixfield e is now in the space H−1(Ω)instead of the space L2(Ω)and the dualityH−1(Ω)〈e,s〉H10(Ω)replaces the inner productRΩe.sdx.

Property(f)constitutes the natural vector version of the surjectivity of the operator div:(Ω)→ {f ∈ L2(Ω);fdx=0},a fundamental property which goes back to Ladyzhenskaya[17],Ladyzhenskaya and Solonnikov[18],Temam[24],Bagovskii[5].

Note that the implications(b)implies(c),(c)implies(d),and(d)implies(e),in Theorem 3.1 were already established,albeit in a slightly different form,in[3];in particular,the introduction of the space denoted(Ω),instead of the quotient space L2(Ω)/Ker∇sin[3],somewhat simplifies the arguments.Otherwise,the implications(e)implies(f),(f)implies(g),and(g)implies(a),are new.

The definition of a domain in RNhas been given in Section 1.

Theorem 3.1(Equivalence Theorem)LetΩbe a domain inRN.The following properties are equivalent:

(a)Vector version of J.L.Lions lemma:

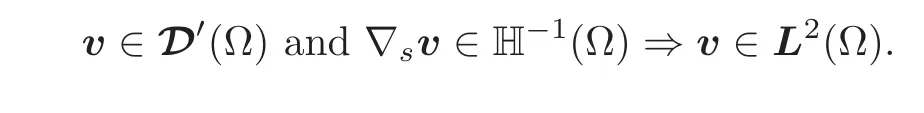
(b)Weak vector version of J.L.Lions lemma:

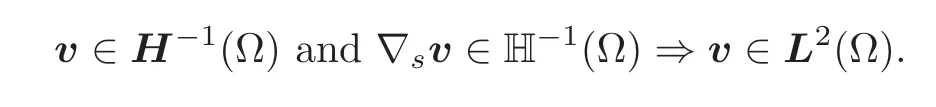
(c)Vector version of Neas inequality:There exists a constantC0(Ω)such that

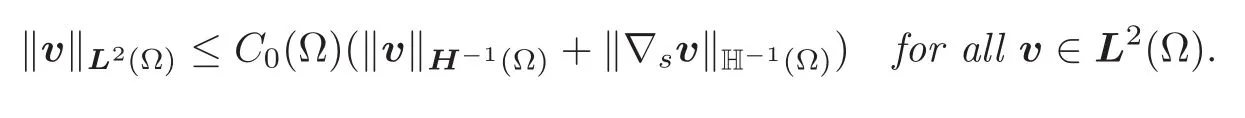
(d)The operator∇shas a closed range:The image of the space

under the operator∇sis a closed subspace of the spaceH−1(Ω).

(e)Weak Donati compatibility conditions:Given a symmetric matrixfielde ∈ H−1(Ω),there exists a vectorfieldv ∈(Ω)such that

if(and clearly only if)

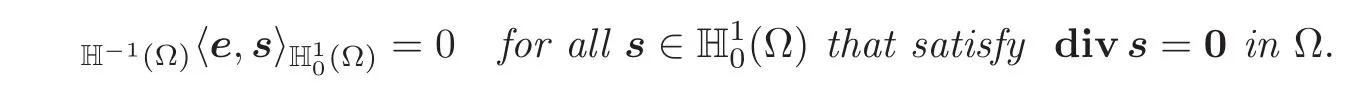
If this is the case,the vectorfieldvis uniquely determined in the space(Ω).

(f)The operator

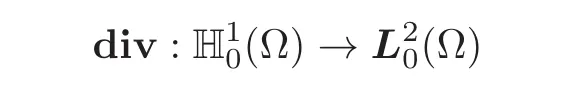
is onto:Consequently,for each vectorfieldv ∈(Ω),there exists a unique symmetric matrixfielde(v)in the orthogonal complement(Kerdiv)⊥ofKerdivin the Hilbert space(Ω)that satisfies

and there exists a constantC1(Ω)such that

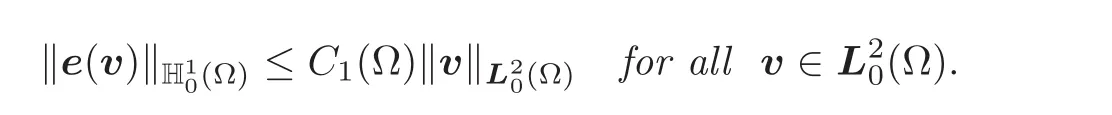
(g)Approximation property:Assume that the domainΩis starlike with respect to an open ball.Then there exists a constantC2(Ω)with the following property:Given any vectorfieldϕin the space

there exist symmetric matrixfieldsen(ϕ)∈ D(Ω),n ≥ 1,such that

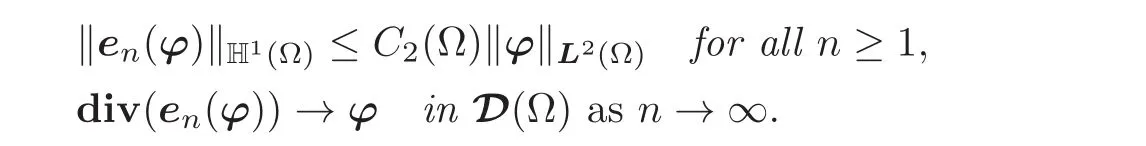
Proof(a)implies(b):Obvious.

(b)implies(c).It is easily verified that the space

equipped with the norm ‖ ·‖H−1(Ω)+ ‖∇s·‖H−1(Ω)is a Banach space.Since the canonical injection ι:L2(Ω) → V(Ω),which is clearly continuous,is onto by(b),the open mapping theorem shows that the inverse mapping ι−1is continuous,which is precisely what inequality(c)expresses.

(c)implies(d).First,note that(Ω)is the orthogonal complement of Ker∇sin L2(Ω);consequently(Ω)is closed in L2(Ω)and the restriction to(Ω)of the operator∇s:L2(Ω) →H−1(Ω)is one-to-one.

Second,by a well-known property of linear operators between Banach spaces,property(d)holds if

Assume by contradiction that such a constant C(Ω)does not exist.Then there exists in this case a sequenceof vector fields vk∈(Ω)that satisfy

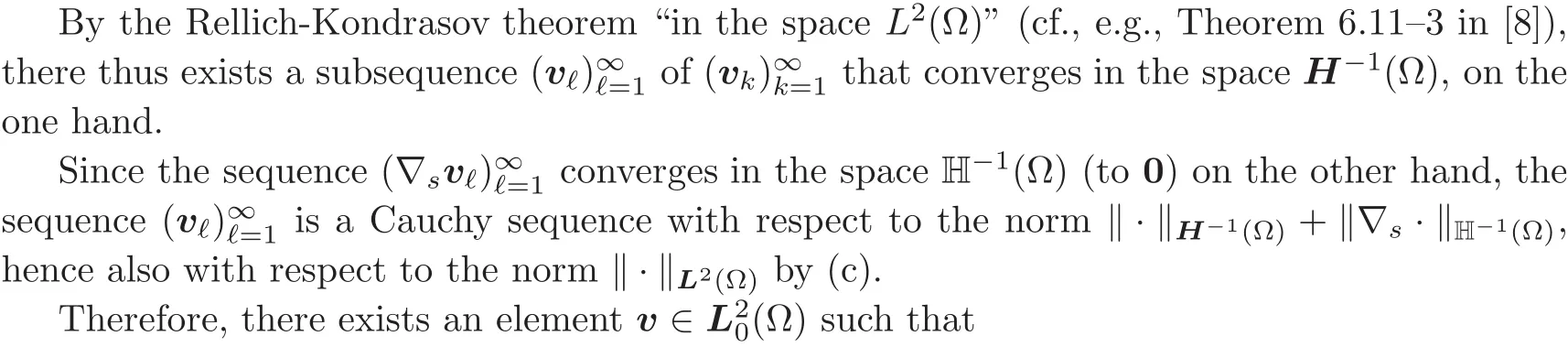
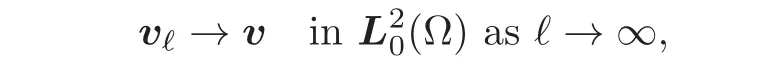
and thus,

Next,given any vectorfield v=(vi)∈(Ω)and any matrix field e=(eij)∈(Ω),

Banach closed range theorem then shows that the operator∇shas a closed range(property(d))if and only if

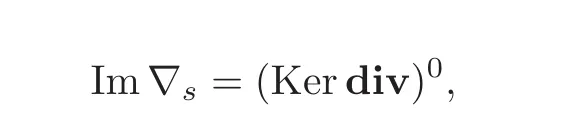
which is exactly property(e).

(e)implies(f).The relations above also mean that−div:(Ω)→(Ω)is the dual operator of∇s:(Ω)→ H−1(Ω).Banach closed range theorem then shows that

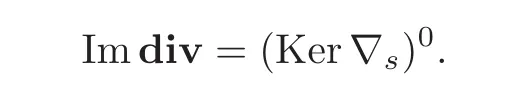
But∇s:(Ω)→ H−1(Ω)is one-to-one,as already noted.Therefore

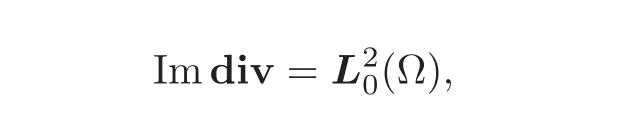
as was to be proved.The continuous operator div:(Kerdiv)⊥→(Ω)is thus onto.

Since the same operator is also one-to-one,the open mapping theorem shows that it has a continuous inverse,which is precisely what the other assertions in(f)express.

(f)implies(g).There is no loss of generality in assuming that Ω is starlike with respect to a ball B(0;r),i.e.,centered at the origin.

Let ϕ ∈ D0(Ω)be given and kept fixed in the ensuing argument.Since D0(Ω) ⊂(Ω),there exists a unique matrix field e=(eij)∈ (Kerdiv)⊥⊂(Ω)such that

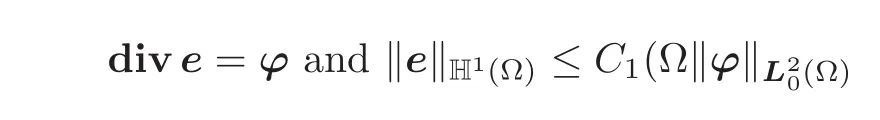
with a constant C1(Ω)independent of ϕ ∈ D0(Ω).Of course,the matrix field e,like the matrixfields snand enintroduced below,all depend on ϕ.

Given any integer n0≥ 1 that satisfies n0＞,let

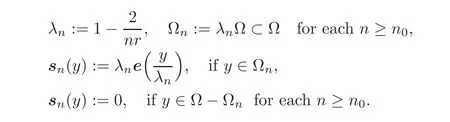
For all n≥n0,we thus have

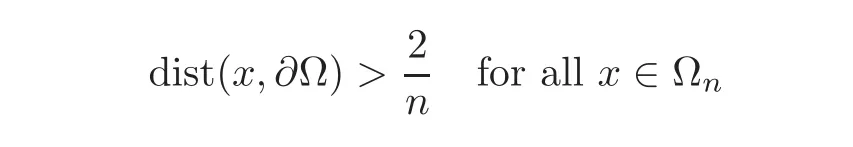
(the assumption that Ω is starlike with respect to B(0;r)is used here),and

and let,for each n≥n0,

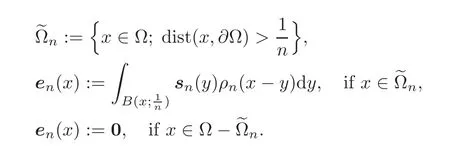
In other words,

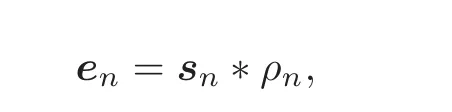
where∗designates the convolution product.

Then the smoothing property of such convolution products and the inclusions suppen⊂together imply that

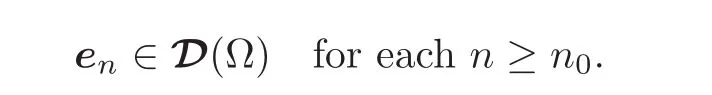
Besides,by another well-known property of convolution products,

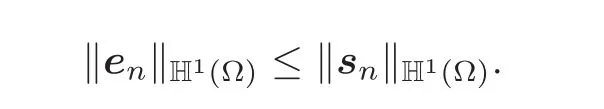
Taking as a new variable y=xλn∈Ω for each x∈Ωngives

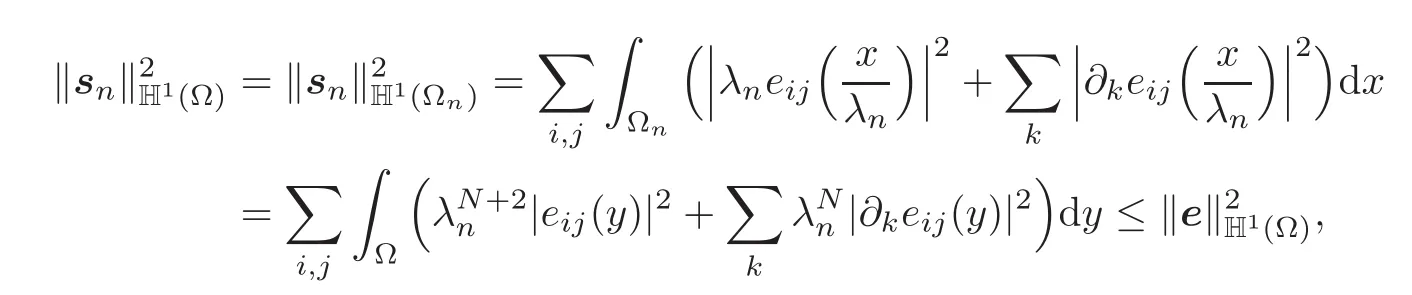
so that,as announced,

It remains to show that

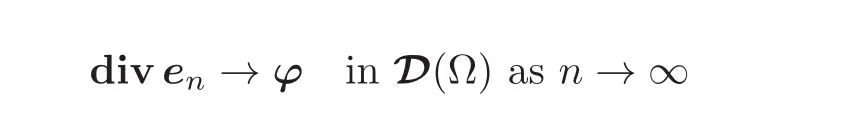
(the definition of convergence in the space D(Ω)is recalled in Section 2).

Since suppϕ⋐Ω and

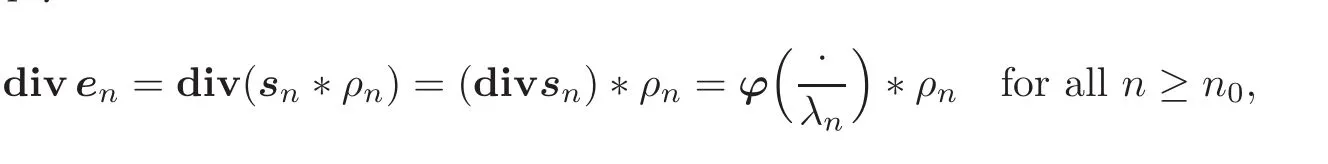
there exist a constant α ＞ 0 and an integer n1≥ n0such that

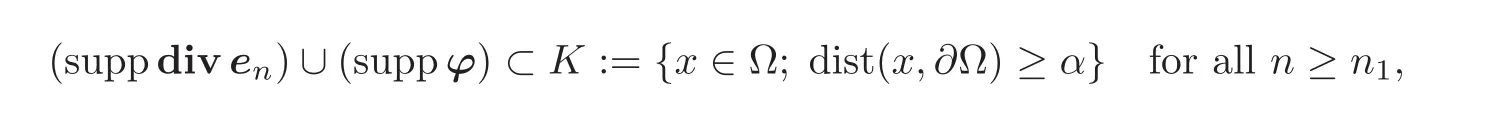
on the one hand.

Using yet another well-known property of convolution products with mollifiers,we infer that,for each multi-index α and each integer n ≥ n1,

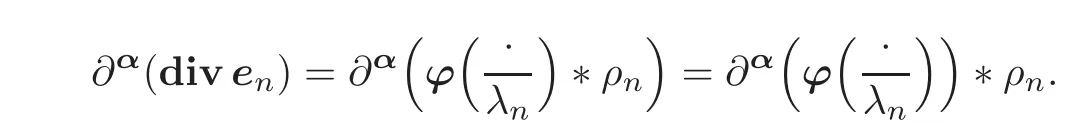
Using thatRΩρn(y)dy=1,we may thus write

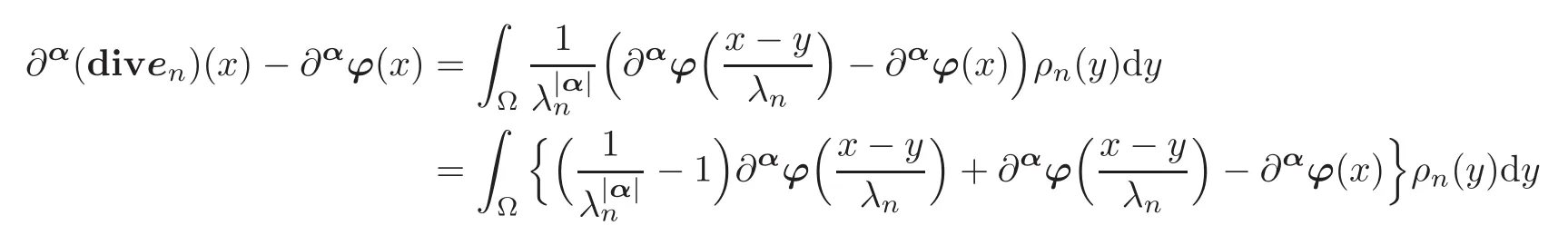
at each x∈Ω.Consequently,

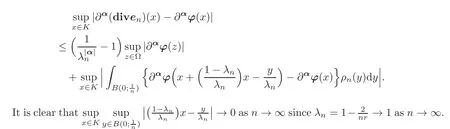
Together,this property and the uniform continuity and boundedness of each partial derivative∂αϕ on Ω therefore imply that

on the other hand.

We have thus shown that diven→ϕ in D(Ω)as n→∞.

(g)implies(a).Let a vectorfield v ∈ D′(Ω)such that∇sv ∈ H−1(Ω).In order to show that v ∈ L2(Ω),it suffices to show that there exists a constant C(Ω,v)such that

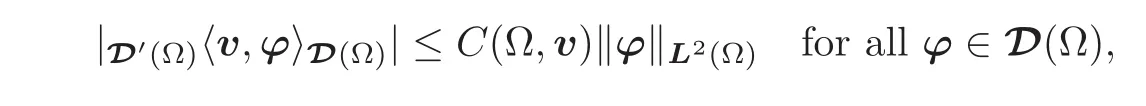
thanks to the density of D(Ω)in L2(Ω)and to F.Riesz representation theorem.

To this end,we proceed in three stages,numbered(i)–(iii).

(i)There exists a constant c0(Ω)independent of v with the following property:Given any ϕ ∈ D(Ω),there exists a vectorfield

Assume without loss of generality that 0 ∈ Ω.It is easily seen,by defining appropriate products of N even or odd functions in D(R)with small enough support,that there exist functions θi∈ D(Ω),1 ≤ i≤ N,that satisfy

Let ekdenote the basis vectors of RN.Then the vector fields defined by

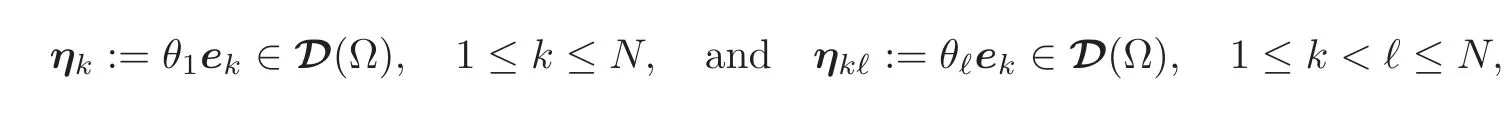
satisfy respectively

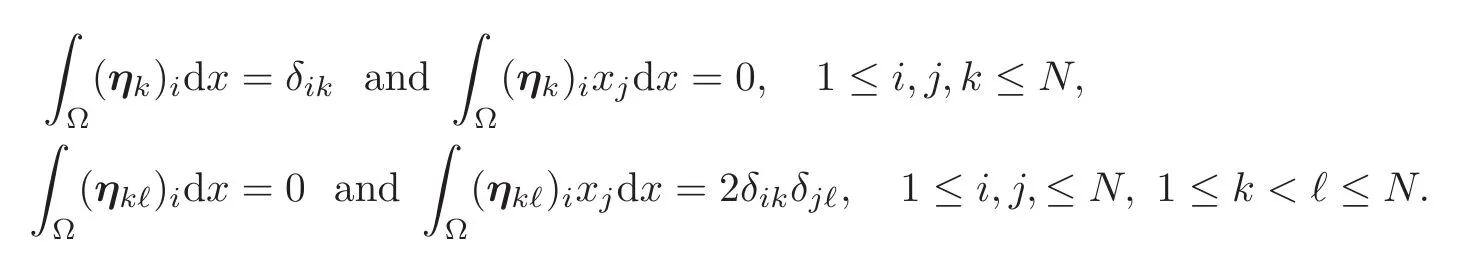
Given any vectorfield ϕ =(ϕi)∈ D(Ω),let the vectorfield∈ D(Ω)be defined by

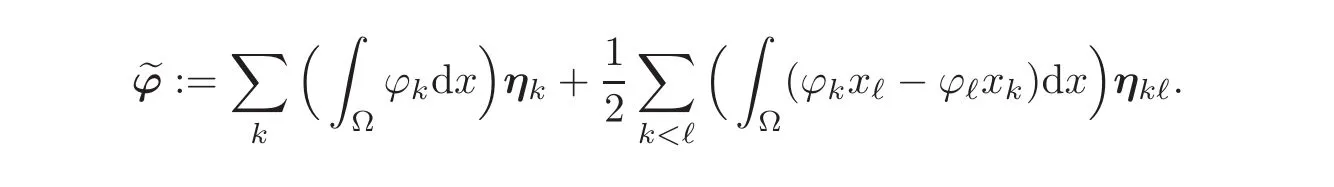
We then claim that the vectorfield(ϕ−)∈D(Ω)satisfies the announced properties:First,

Second,given any numbers aijsatisfying aij=−aji,1≤i,j≤N,

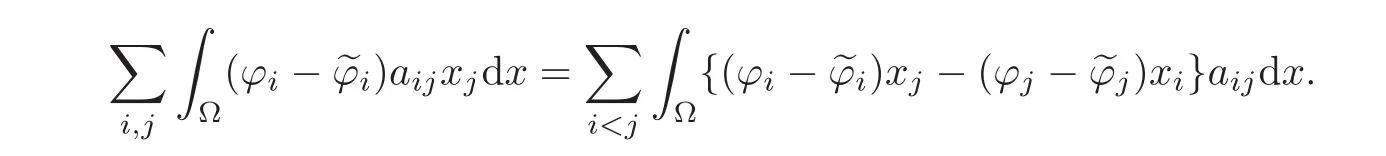
Noting that

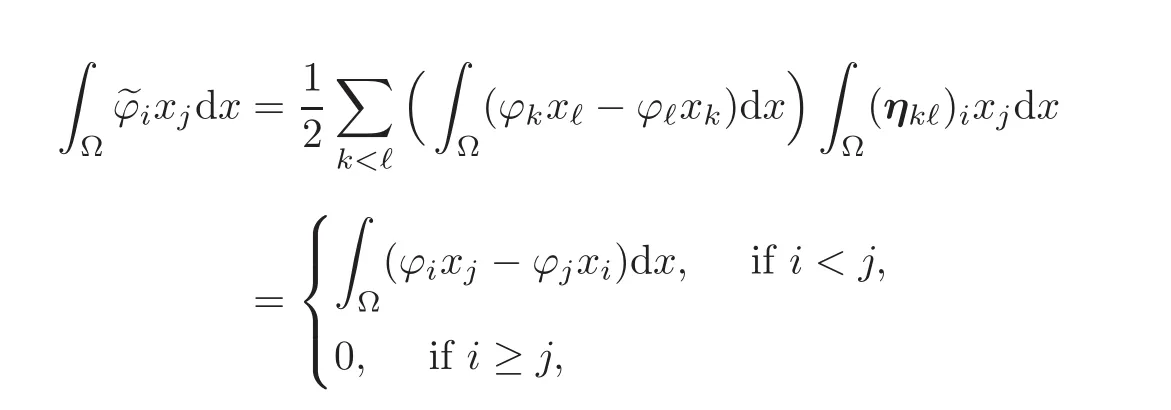
and that,likewise,

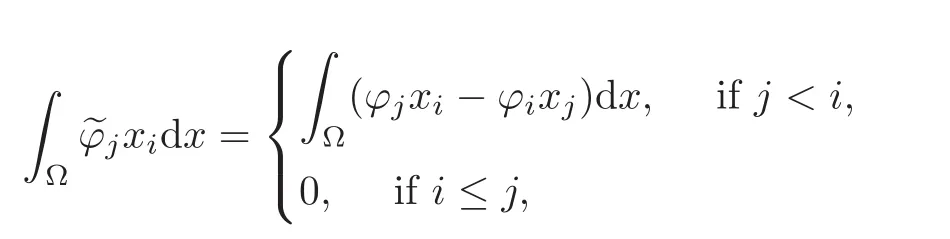
we infer that

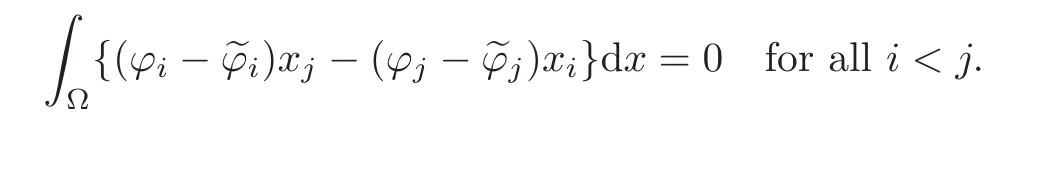
We have thus shown that

(ii)Assume that Ω is starlike with respect to a ball.Since(ϕ −)∈D0(Ω),there exist by(g)matrixfields en∈D(Ω),n≥1,that depend on(ϕ −),hence on ϕ,such that

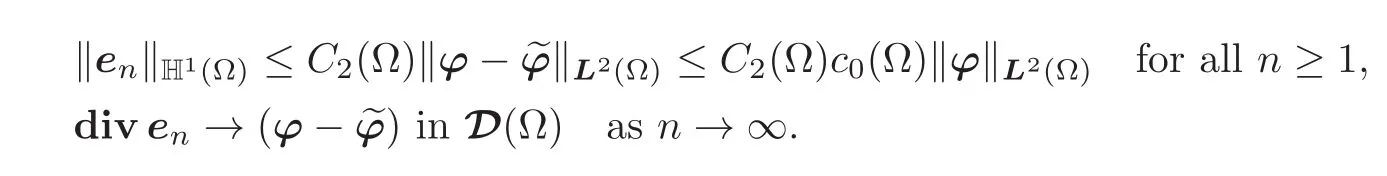
Given any ϕ ∈ D(Ω),the scalar 〈v,ϕ〉can therefore be written as

where,for notational brevity,we let

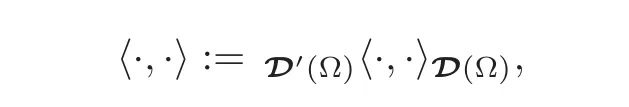
like in the rest of this part of the proof.Let us examine the two terms appearing in the above expression of〈v,ϕ〉.

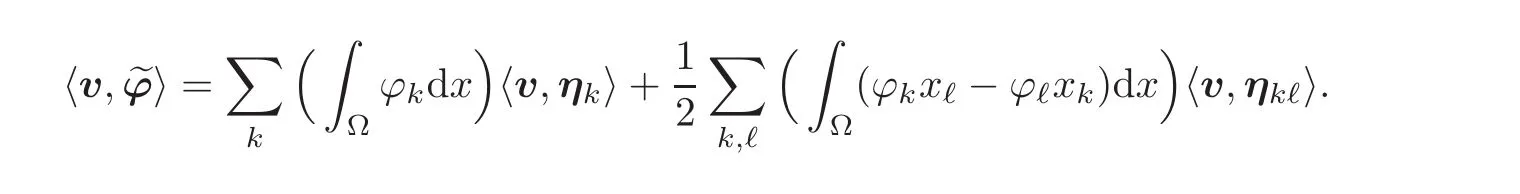
Hence there exists a constant c1(Ω,v)such that

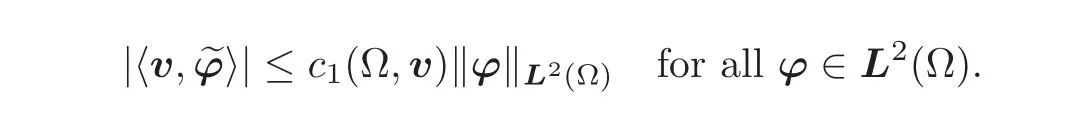
Second,the assumption that∇sv∈ H−1(Ω)implies that

hence that

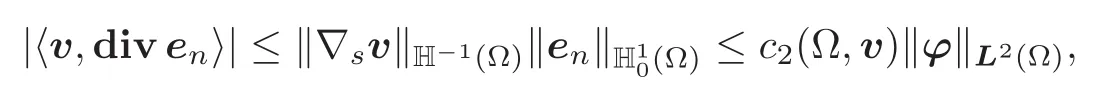
with c2(Ω,v):= ‖∇sv‖H−1(Ω)C2(Ω)c0(Ω).

Consequently,

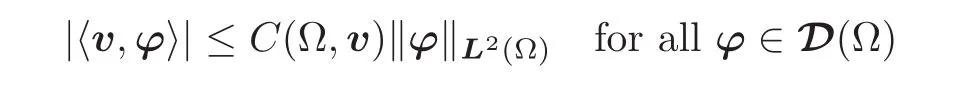
with C(Ω,v):=c1(Ω,v)+c2(Ω,v).We have thus shown that the vector version of J.L.Lions lemma holds on a domain that is starlike with respect to a ball.

(iii)Finally,assume that Ω is a general domain.In this case,arguments similar to those used in Maz’ya[20]or Costabel and McIntosh[9]show that Ω can be written as a finite union

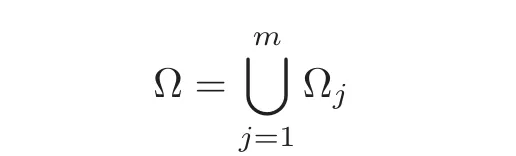
of domains Ωj⊂ Ω,1≤ j≤ m,each of which is starlike with respect to a ball.

Given any open subset U of Ω and any vector field θ ∈ D(U),the notation θ♯designates in what follows the extension of θ by 0 on Ω − U,so that θ♯∈ D(Ω).

For each 1≤j≤m,the linear form

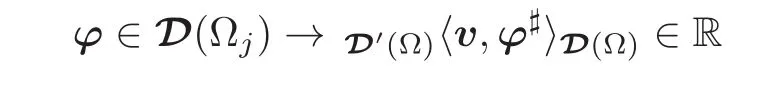
defines a distribution,denoted vj,on Ωj,which therefore satisfies

Consequently,given any matrix field e ∈ D(Ωj),

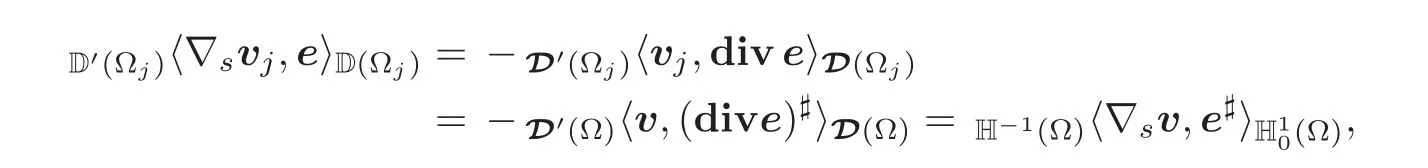
and thus

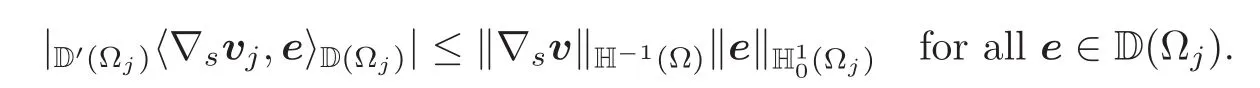
The last relation shows that∇svj∈ H−1(Ωj).The vector version of J.L.Lions lemma on the domain Ωj(see(ii))thus implies that each vector field vj∈ D′(Ωj)can be identified with a vector field in L2(Ωj),in the sense that

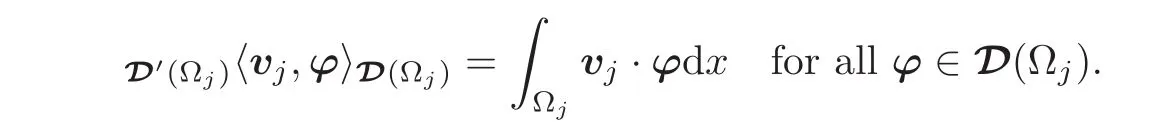
Besides,given any 1≤j,k≤N,the relation

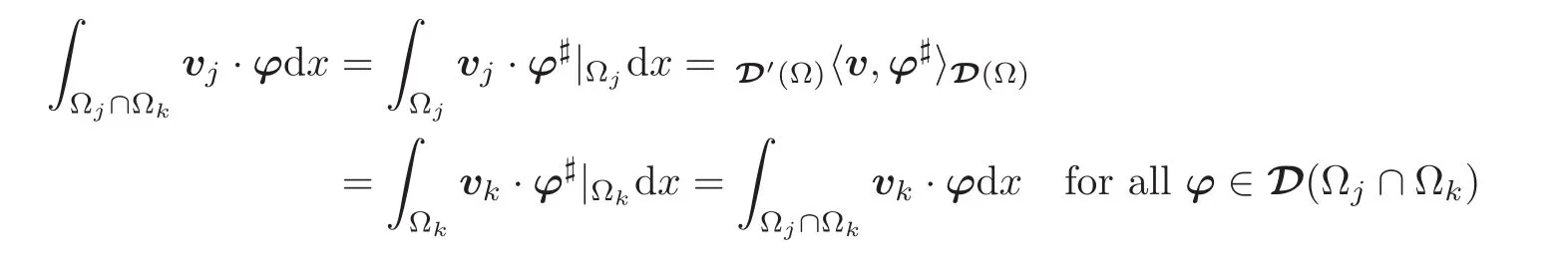
shows that vj=vkin Ωj∩ Ωk.The relations w|Ωj:=vj,1 ≤ j≤ m,therefore unambiguously define a vectorfield w ∈ L2(Ω).

It remains to show that v=w.Given any vector fielda partition of unity associated with the open covering suppi.e.,made up with functions αj∈ D(Ω),1≤ j≤ m,that satisfy

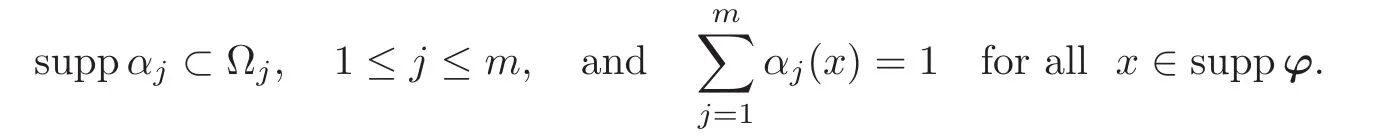
We then have

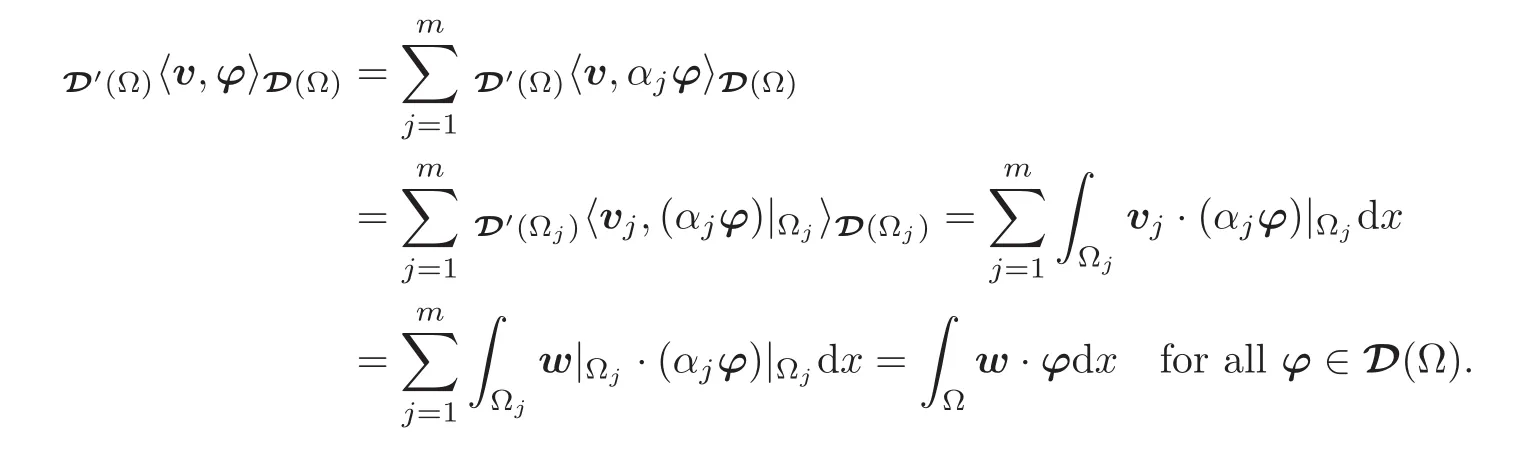
Consequently,v=w ∈L2(Ω)as announced.This completes the proof.

4 Two Further Equivalences

To conclude,we also state two further properties that are also equivalent to the vector version of J.L.Lions lemma.

Thefirst equivalence asserts that the“weak”version of the Donati compatibility conditions(e)of Theorem 3.1 can be replaced by an even “weaker” version,in the sense that the “trialfields” s need be only in the space D(Ω)instead of in the space(Ω).More specifically,we have the following theorem.

Theorem 4.1LetΩbe a domain inRN.The vector version of J.L.Lions lemma,viz.,

is equivalent to the following version of the Donati compatibility conditions:Given a matrixfielde∈ H−1(Ω),there exists a vectorfieldv ∈Ω)such that

if(and clearly only if)

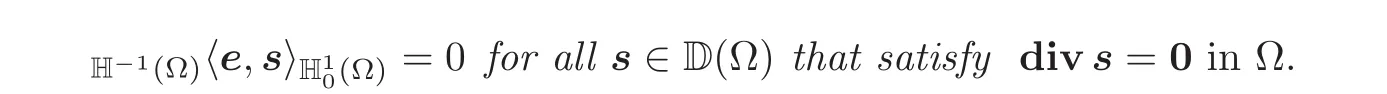
If this is the case,the vectorfieldvis uniquely determined in the space(Ω).

ProofThe principle of the proof is identical to that of the proof of Theorem 4.1 in[2],or similar to that of the proof of Theorem 2.3 in Chapter 1 of Girault and Raviart[15];for this reason,the proof is omitted.Suffices it to mention that establishing the sufficiency of the above Donati conditions relies not only on the vector version of J.L.Lions lemma itself,but also on the one of its consequences,viz.,the sufficiency of the weak Donati compatibility conditions(e)established in Theorem 3.1.

The second equivalence asserts that the vector version of J.L.Lions lemma is equivalent to a weak version of the well-known Saint-Venant compatibility conditions,“weak” in the sense that the matrix field e is now given in the space H−1(Ω),instead of in the space L2(Ω)as in[3],where such conditions played a crucial role for defining an intrinsic approach to linearized elasticity(a quick introduction to the Saint-Venant compatibility condition is found in Subsection 6.19 of[8]).

Theorem 4.2LetΩbe a simply-connected domain inRN.Then the vector version of J.L.Lions lemma,viz.,

is equivalent to the following weak Saint-Venant compatibility conditions:Given a matrixfielde=(eij)∈ H−1(Ω),there exists a vectorfieldv ∈(Ω)such that∇sv=eif(and clearly only if)

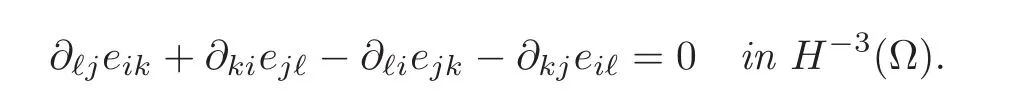
If this is the case,the vectorfieldvis uniquely determined in the space(Ω).

ProofThis equivalence was already established in Theorem 7.3 of[3]in the special case where N=3,by means of arguments,essentially based on a clever idea due to Kesavan[16],that can be easily extended to any integer N≥2 and which,for this reason,will not be reproduced here.We simply emphasize that the assumption of simple-connectedness of the domain Ωis crucially needed here,as the proof relies on the sufficiency of the “classical” Saint-Venant compatibility condition,which itself relies on the “classical” Poincar´e lemma(for details,see again Subsection 6.19 of[8]).

[1]Adams,R.A.,Sobolev Spaces,Academic Press,New York,1975.

[2]Amrouche,C.,Ciarlet,P.G.and Mardare,C.,On a lemma of Jacques-Jouis Lions and its relation to other fundamental results,J.Math.Pures Appl.,104,2015,207–226.

[3]Amrouche,C.,Ciarlet,P.G.,Gratie,L.and Kesavan,S.,On the characterizations of matrixfields as linearized strain tensor fields,J.Math.Pures Appl.,86,2006,116–132.

[4]Amrouche,C.and Girault,V.,Decomposition of vector spaces and application to the Stokes problem in arbitrary dimension,Czechoslovak Math.J.,44,1994,109–140.

[5]Bogovskii,M.E.,Solution of thefirst boundary value problem for the equation of continuity of an incompressible medium,Soviet Math.Dokl.,20,1979,1094–1098.

[6]Borchers,W.and Sohr,H.,On the equations rotv=g and divu=f with zero boundary conditions,Hokkaido Math.J.,19,1990,67–87.

[7]Bramble,J.H.,A proof of the inf-sup condition for the Stokes equations on Lipschitz domains,Math.Models Methods Appl.Sci.,13,2003,361–371.

[8]Ciarlet,P.G.,Linear and Nonlinear Functional Analysis with Applications,SIAM,Philadelphia,PA,2013.

[9]Costabel,M.and McIntosh,A.,On Bogovski˘ı and regularized Poincar´e integral operators for de Rham complexes on Lipschitz domains,Math.Z.,265,2010,297–320.

[10]Duvaut,G.and Lions,J.L.,Les In´equations en M´ecanique et en Physique,Dunod,Paris,1972.

[11]Geymonat,G.and Gilardi,G.,Contre-exemple`a l’in´egalit´e de Korn et au lemme de Lions dans des domaines irr´eguliers,Equations aux D´eriv´ees Partielles et Applications,Articles D´edi´es`a Jacques-Louis Lions,pp.541–548,Gauthier-Villars,Paris,1998.

[12]Geymonat,G.and Krasucki,F.,Some remarks on the compatibility conditions in elasticity,Rend.Accad.Naz.Sci.XL Mem.Mat.Appl.,29,2005,175–181.

[13]Geymonat,G.and Krasucki,F.,Beltrami’s solutions of general equilibrium equations in continuum mechanics,C.R.Acad.Sci.Paris,S´er.I,342,2006,259–363.

[14]Geymonat,G.and Suquet,P.,Functional spaces for Norton-Hoffmaterials,Math.Methods Appl.Sci.,8,1986,206–222.

[15]Girault,V.and Raviart,P.A.,Finite Element Methods for Navier-Stokes Equations,Springer-Verlag,Berlin,1986.

[16]Kesavan,S.,On Poincar´e’s and J.L.Lions’lemmas,C.R.Acad.Sci.Paris,S´er.I,340,2005,27–30.

[17]Ladyzhenskaya,O.A.,The Mathematical Theory of Viscous Flows,Second Edition,Gordon and Breach,New York,1969.

[18]Ladyzhenskaya,O.A.and Solonnikov,V.A.,Some problems of vector analysis and generalized formulations of boundary value problems for the Navier-Stokes equations,J.Soviet.Math.,10,1978,257–286.

[19]Magenes,E.and Stampacchia,G.,I problemi al contorno per le equazioni differenziali di tipo ellittico,Ann.Scuola Norm.Sup.Pisa,12,1958,247–358.

[20]Maz’ya,V.,Sobolev Spaces,Springer-Verlag,Heidelberg,1985.

[21]Neˇcas,J.,Equations aux D´eriv´ees Partielles,Presses de l’Universit´e de Montr´eal,1965.

[22]Neˇcas,J.,Les M´ethodes Directes en Th´eorie des Equations Elliptiques,Masson,Paris and Academia,Praha,1967(English translation:Direct Methods in the Theory of Elliptic Equations,Springer-Verlag,Heidelberg,2012).

[23]Tartar,L.,Topics in Nonlinear Analysis,Publications Math´ematiques d’Orsay No.78.13,Universit´e de Paris-Sud,D´epartement de Math´ematique,Orsay,1978.

[24]Temam,R.,Navier-Stokes Equations,North-Holland,Amsterdam,1977.

[25]Vo-Khac,K.,Distributions – Analyse de Fourier – Op´erateurs aux D´eriv´ees Partielles,Volume 1,Vuibert,Paris,1972.