The Iteration Formulae of the Maslov-Type Index Theory in Weak Symplectic Hilbert Space∗

Li WU Chaofeng ZHU

1 Introduction

Since the pioneer work[3]on iteration of closed geodesics,the theory was generalized to convex Hamiltonian case(see[5]),to symplectic paths(see[13]),and to brake orbits(see[11]).The iteration theory for symplectic paths turns out to be extremely useful in the study of the periodical solutions of the finite dimensional Hamiltonian systems[5,7–8,11–12,14–17].

All the known proofs of the iteration formulae follow the following line.Firstly,they give the relation between the(relative)Morse index for a certain differential operator and the Maslovtype index of its fundamental solution.Then they show that such an operator is in diagonal form under the iteration with respect to a certain orthogonal decomposition of the subspaces.The iteration formulae then follow from the above argument.

In this paper,we shall give a direct proof of the iteration formulae.The idea is that each splitting formula of the nullity will induce a splitting formula of the Maslov-type indices.The iteration formula then follows from the homotopy invariance of the Maslov-type indices.

Our method has three advantages.Firstly,we do not require that the symplectic path starts from the identity.So we can treat the iteration theory for symplectic paths in symplectic Hilbert spaces.It will be used in the study of the periodical solutions of the infinite dimensional Hamiltonian systems.Secondly,we do not need the orthogonality of the decomposition.So we can get more general formulae in some cases.It can be applied to non-contractible periodical solutions of Hamiltonian systems.Finally,our results apply to symplectic paths on weak symplectic Hilbert space.

2 A Splitting Formula of the Maslov-Type Index Induced by the Splitting of the Nullity

In this paper,we denote by dimV the complex dimension of a complex vector space V.A pair of complex linear subspaces(λ,µ)of V is called Fredholm if dim(λ∩µ)and dimV/(λ+µ)are finite.The index of the pair(λ,µ)in V is defined as

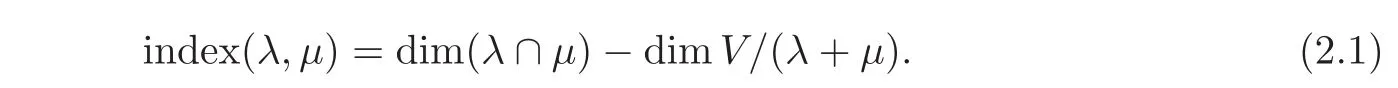
Let(H,〈·,·〉)be a complex Hilbert space with a bounded injective map J such that J∗= −J.Then we have the symplectic structure ω on H defined by ω(x,y):= 〈Jx,y〉for each x,y ∈ H.Since J∗is injective,imJ is dense in H.The operator J−1on H is a closed operator with dense domain imJ.The annihilator of a linear subspace λ of H is defined by

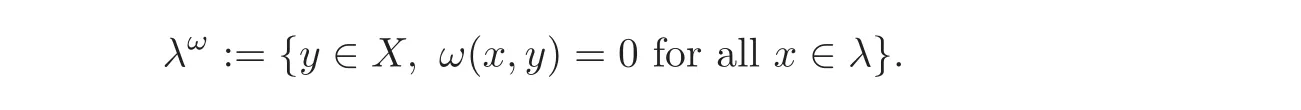
The subspace λ is called a Lagrangian subspace of H if λ = λω.We denote by L(H)the set of the Lagrangian subspaces of H.We define

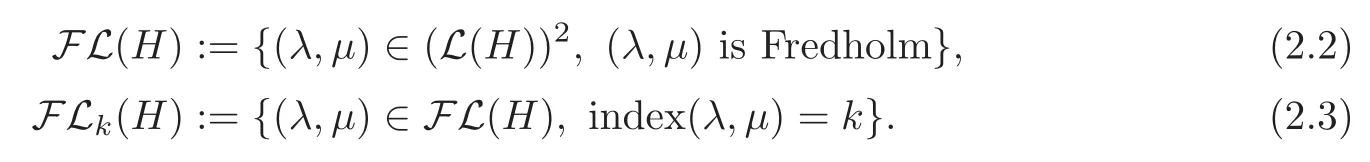
Denote by GL(H),B(H),S(H),P(H)and U(H)the set of bounded invertible operators,bounded operators,bounded self-adjoint operators,positive definite operators and unitary operators on H respectively.The symplectic group Sp(H)and the symplectic Lie algebra sp(H)are defined as

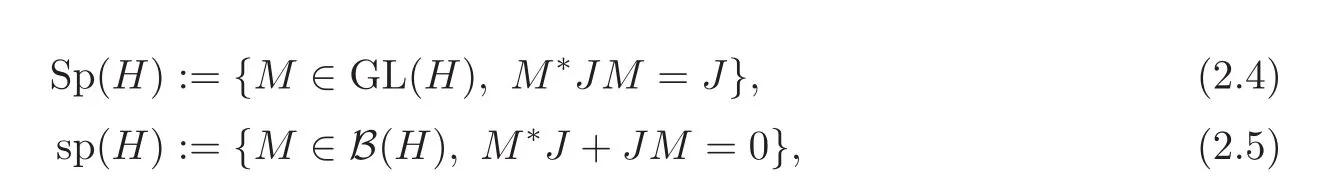
respectively.Then we have J∈sp(H)and eJs∈Sp(H)for s∈R.The path eJs,s∈R is crucial in our main result,Theorem 2.2 below.So our method does not work in the general symplect Banach space case.For each M ∈B(H)such that M∗JM=J,the operator M is injective.If dimH is infinite and J is invertible,there exists an M ∈B(H)GL(H)such that M∗JM=J.For each M ∈ Sp(H),we have M−1=J−1M∗J and im(M∗J)⊂ imJ.Let z∈ C and|z|=1.Then we have zIH∈Sp(H),where IHdenotes the identity map on H.The fact is used in Definition 2.1 below.So we use the concept of complex symplectic Hilbert space instead of the real one.

Let λ(s),s ∈ (−ε,ε)be a path in L(H)differentiable at s=0 and λ(0)be an L-complemented Lagrangian subspace,i.e.,there exists aµ ∈ L(H)such that H= λ(0)⊕ µ.If J is an isomorphism,each Lagrangian subspace of H is an L-complemented Lagrangian subspace.Define the form q(λ,0)on λ(0)by

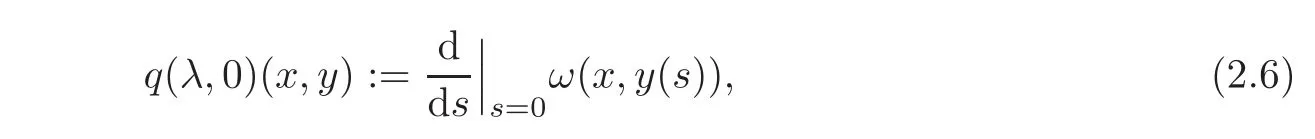
where x,y ∈ λ(0),y(s)∈ λ(s)and y(s)− y ∈ µ.Then the form q(λ,0)is independent of the choices ofµ ∈ L(H)with H= λ(0)⊕ µ.The path λ is said to be(semi-)positive(see[1,Definition 3.2.8])if q(λ,s)is(semi-)positive definite for each s ∈ (−ε,ε).

Lemma 2.1Letγ(s),s ∈ (−ε,ε)be a path inSp(H)differentiable ats=0withγ(0)=IHandλ(0)be an L-complemented Lagrangian subspace.Setλ(s):= γ(s)λ(0)for eachs ∈ (−ε,ε).Then we have

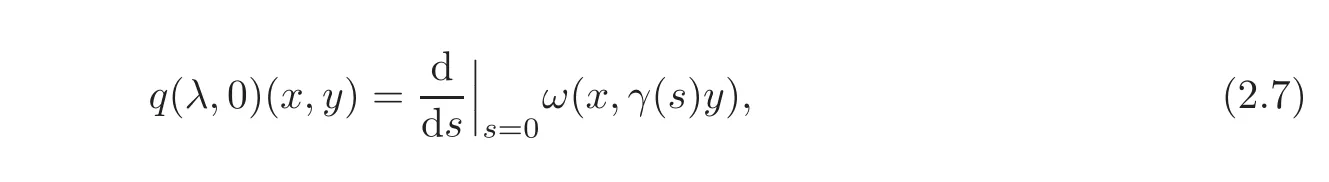
wherex,y∈ λ(0).

ProofLet µ ∈ L(H)be such that H= λ(0)⊕ µ.Let γ(s)be of the form

For x,y ∈ λ(0),let y(s)∈ λ(s)be such that y(s)−y ∈ µ.Then we have y(s)=y+C(s)A(s)−1y,and ω(x,y(s)− γ(s)y)= ω(x,C(s)(A(s)−1− Iλ(0))y).By(2.6),our result(2.7)holds.

Set X:=H × H.We define the symplectic structure of X by

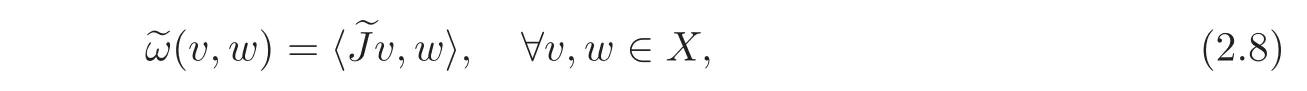
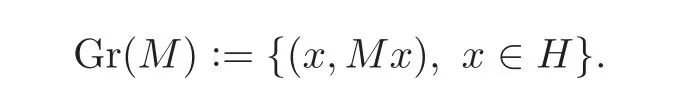
By[2,Lemma 4],Gr(M)is an L-complemented Lagrangian subspace of X.

Definition 2.1(see[19,Definition 4.6])Let(H,ω)and(X,be symplectic Hilbert spaces as defined above.LetVbe a Lagrangian subspace ofX.Letγ(t),t∈ [a,b]be a path inSp(H).Assume that(Gr(γ(t)),V)is a Fredholm pair for eacht∈ [a,b].Denote byMas{·,·}the Maslov index for the path of Fredholm pairs of Lagrangian subspaces inXwith index0defined by[1,Definition 3.1.4].The Maslov-type indexiV(γ)is defined by

For eachM∈Sp(H),we define the nullityνV(M)and co-nullityeνV(M)by

IfN∈Sp(H)andV=Gr(N),we defineiN(γ):=iV(γ),νN(M):=νV(M)and(M):=(M).Ifz ∈ C,|z|=1andV=Gr(zIH),we defineiz(γ):=iV(γ),νz(M):= νV(M)and(M):=(M).

By[19,Lemma 4.4],for each N ∈Sp(H)and γ ∈C([a,b],Sp(H)),we have

By[2,Proposition 1],for each V∈L(X)and M∈Sp(H),we have

Definition 2.2(see[3,Definition 3.1])Let(H,ω)be a symplectic Hilbert space as defined above.AC1pathγ:[a,b]→Sp(H)is called a positive path if˙γ(t)γ(t)−1∈Kfor eacht∈[a,b],where we denote by:=and the coneKis defined by

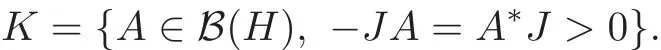
By[4,Lemma 3.1],the path γ is positive if and only if Gr(γ)is positive.

The following lemma is our key observation.

Lemma 2.2Let(H,ω)be a symplectic Hilbert space as defined above.Letγ1(t),γ2(t)witht∈ [a,b]be two positive paths inSp(H).Thenγ(t):= γ1(t)γ2(t),t∈ [a,b]is a positive path.

ProofWe have

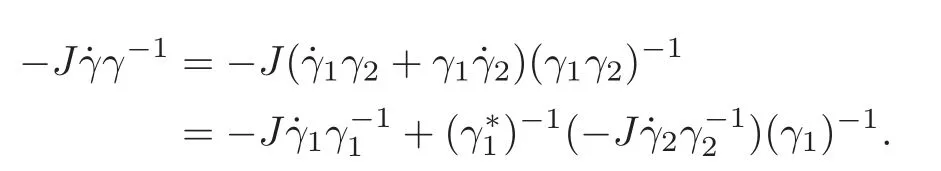
Since γ1,γ2are both positive paths,are both positive definite.So−J˙γγ−1is positive definite and the lemma follows.

We need a special case of[1,Theorem 3.2.12].

Theorem 2.1Let(H,ω)and()be two symplectic Hilbert space.For0≤a≤δ,δ＞0,we are given continuous two-parameter families

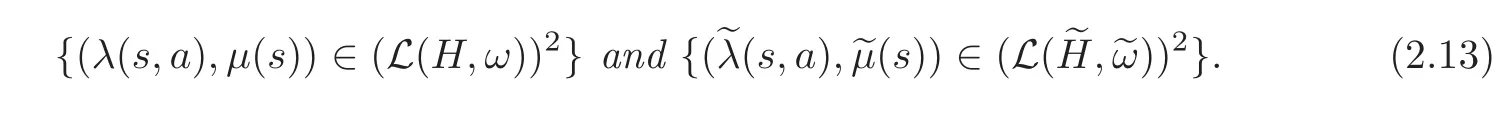
We assume

Then we have

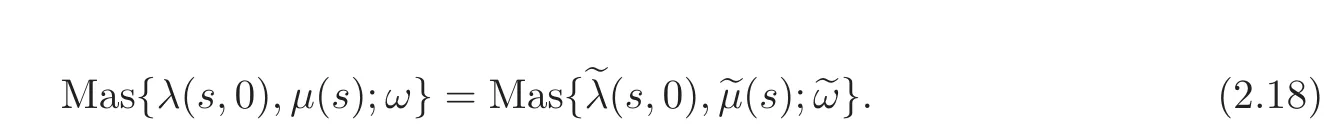
The main result of the paper is as follows.Note that the path MeJs,s∈R is positive for each M∈Sp(H).

Theorem 2.2(Splitting of the Maslov-Type Index Induced by Splitting of the Nullity)Let(H,ω)and(X,)be symplectic Hilbert spaces as defined above.Letfj:Sp(H)→Sp(H)(j=1,···,k)be a family ofC1maps,wherekis a positive integer.Assume that there are Lagrangian subspaces{Vj}j=0,···,kofXsuch that the following hold for eachM ∈ Sp(H):

(i)The pairis a Fredholm pair with index0if and only if all pairs(Gr(fj(M)),Vj)are Fredhlom pairs with index0,and

(ii)fj(eJsM),s ∈ Ris positive for eachj=1,···,k.

Letγ ∈ C([a,b],H)such that the pairis a Fredholm pair withindex0for eacht∈[0,1].Then we have

ProofLet X:=X and:=Xk.For each(s,t)∈R×[0,1],set

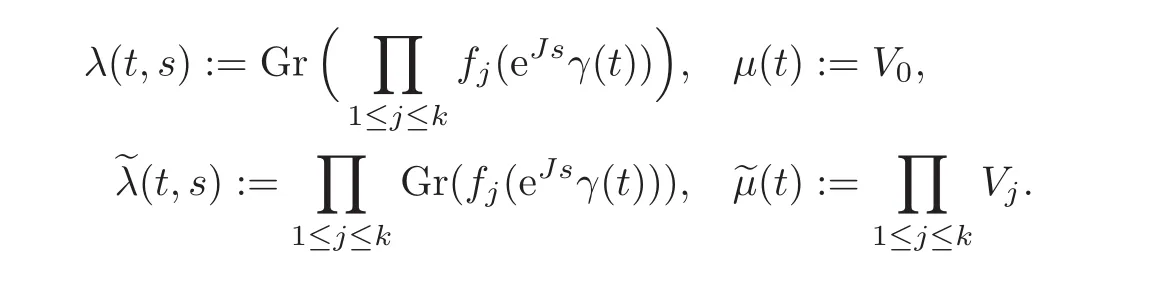
By(i),for each t∈ [0,1],there hold that the pair(λ(t,0),µ(t))is a Fredholm pair of Lagrangian subspace in X,((t,0),(t))is a Fredholm pair of Lagrangian subspace in,and dim(λ(t,s)∩µ(t))=dim((t,s)∩(t)).By(ii)and Lemma 2.2,the two paths λ(t,·)andare both positive for eachfixed t.By[1,Theorem 2.2.1.c],the Maslov index is additive under direct sum.We have

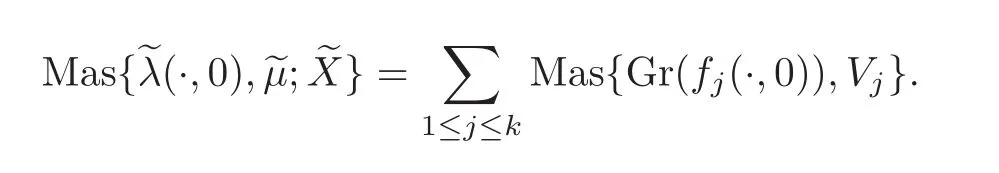
By Theorem 2.1,we have

Remark 2.1Each pair of Lagrangian subspaces of afinite dimensional symplectic space is a Fredhlom pair with index 0.We shall choose suitable functions{fi}to get some classical iteration formulae for the symplectic paths in Section 4.

3 The Global Structure of Sp(H)When ω is Strong

Let(H,ω)be the symplectic Hilbert space defined in Section 2.Assume that ω is strong,i.e.,J is an isomorphism.In this section we give the global structure of Sp(H).

Lemma 3.1Let(H,ω,J)be a strong symplectic Hilbert space.SetJ1:=(−J2)Jandω1(x,y):= 〈J1x,y〉for eachx,y∈ H.Then the following hold:

(a)(H,ω1,J1)is a strong symplectic Hilbert space,

(c)We have a homeomorphism

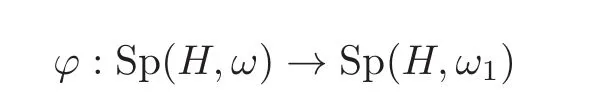
defined byϕ(M)=for eachM ∈ Sp(H,ω).

ProofDirect computation.Note that J(−J2)t=(−J2)tJ for each t∈ R.

By the lemma above,we can assume that J2= −IH.By Kuiper’s theorem,U(H)is contractible if dimH=+∞.By the method similar to that in[14,Section 1.1,Section 2.2],we get the following Proposition 3.1.Here we give a short proof.

Proposition 3.1Let(H,ω)be a symplectic Hilbert space defined in Section2.Assume thatJ2=−IH.SetH±:=dimker(J∓ −1).ThenH=H+⊕H−.

(f)Sp(H)is a real analytic Hilbert manifold modelled on the real Hilbert spacesp(H).Its real dimension ism2ifH=Cm.

Proof(a)By the polar decomposition,each M∈Sp(H)is uniquely represented by M=AU,where A∈P(H)and U∈U(H).Then we obtain

By the uniqueness of the decomposition,we obtain A=J−1AJ and U=J−1(U∗)−1J.Thus both A and U are symplectic.The converse is obvious.

(b)Each A∈P(H)∩Sp(H)is uniquely represented by A=exp(S),where S∈S(H).Since A is symplectic,

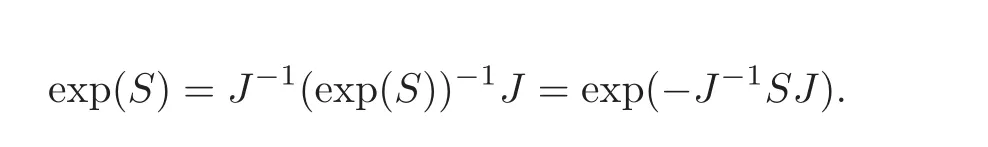
By the uniqueness we obtain S=−J−1SJ and S∈sp(H).The converse is obvious.

(c)Note that U∈U(H)∩Sp(H)if and only if UJ=JU and U∈U(H).Our results then follow from direct calculation.

(d)and(e)(d)follows from(a),(b)and(c),and(e)follows from(d).

(f)Thefirst part of(f)follows from(d).If H=Cm,we denote by m±:=dimH±.Then the real dimension of Sp(H)is

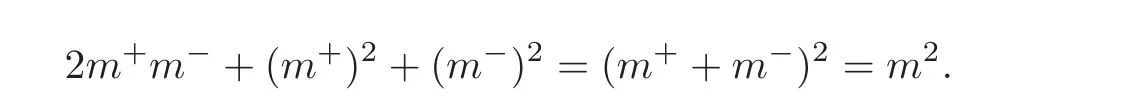
4 The Iteration Formulae for Symplectic Paths

In this section we derive some iteration formulae for symplectic paths from Theorem 2.2.

4.1 Some general facts on the Maslov-type index in thefinite dimensional case

The following lemmas are useful for deriving the iteration formulae from Theorem 2.2.For each τ＞ 0,we define

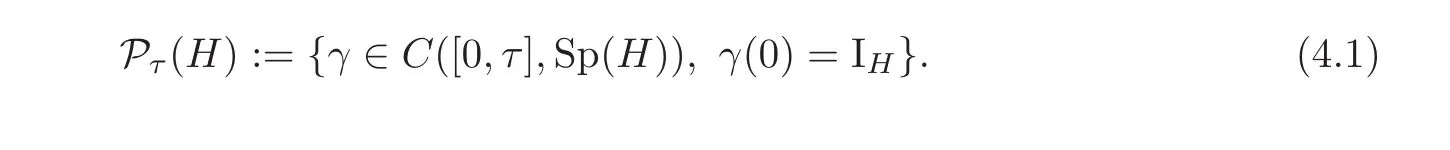
Lemma 4.1Let(H,ω)and(X,)be symplectic Hilbert spaces defined in Section2.Assume thatdimH ＜ +∞.Letφ :Pτ1(H)→ Pτ2(H)be a continuous map such thatφ(c0)=c0,whereτ1,τ2are two positive numbers andc0denotes the constant pathIH.LetVbe a Lagrangian subspace ofX.Denote the curveγ(s·):[0,1]→ Sp(H)byγ(s·)(t):= γ(st).Then for eachγ ∈ Pτ1(H),we have

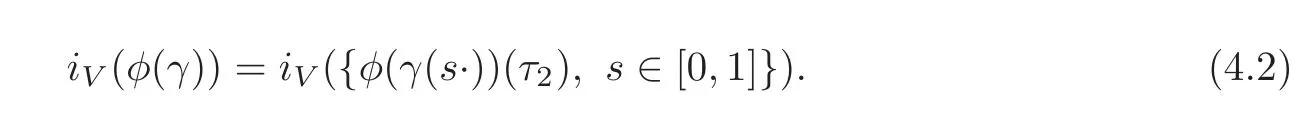
ProofDefine the homotopy h(s,t):[0,1]× [0,τ2]→ Sp(H)by h(s,t):= φ(γ(s·))(t).Then we have h(0,t)=h(s,0)=IH.By the homotopy invariance of the Maslov index,the equation(4.2)follows.

Lemma 4.2Let(H,ω)and(X, eω)be symplectic Hilbert spaces defined in Section2.Letf1,f2:Sp(H)→Sp(H)be a two continuous maps such thatf1(IH)=f2(IH)=IH.LetV1,V2be two Lagrangian subspaces ofX.Assume thatdimH＜+∞.Then the following hold:

(a)Assume that(f1)∗=(f2)∗:π1(Sp(H))→ Z.Then there is an interger valued functionδ:Sp(H)→ Zdefined by

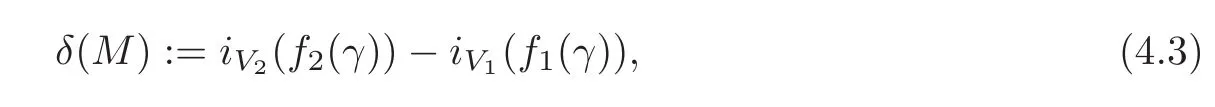
whereγ ∈ Pτ(H),τ＞ 0withγ(τ)=M.

(b)Assume that(f1)∗=(f2)∗:π1(Sp(H))→ Z.Letδ:Sp(H)→ Zbe the function defined in(a).Then for eachγ∈C([a,b],Sp(H)),we have

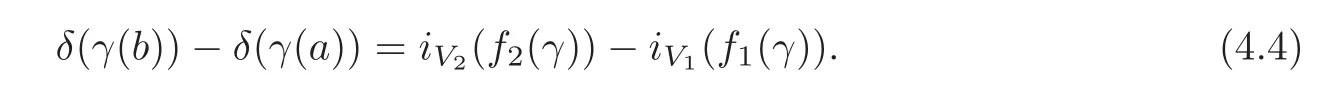
(c)We have(f1f2)∗=(f1)∗+(f2)∗:π1(Sp(H))→ Z.

Proof(a)Let γ1and γ2be in Pτ(H)with γ1(τ)= γ2(τ)=M.Let γ3∈ P2τ(H)be the loop in Sp(H)defined by γ1followed by the reverse of γ2.Then we have[f1(γ3)]=[f2(γ3)]∈π1(Sp(H)).Since L(X)is path connected,there is a path λ :[0,1] → L(X)of Lagrangian subspaces such that λ(0)=V1, λ(1)=V2.Then we have a homotopy h:[0,1]× [0,2τ]→(L(X))2defined by h(s,t)=(λ(s),Gr(γ3(t))).By the homotopy invariance of the Maslov index,we have iV1(f1(γ3))=iV2(f1(γ3))=iV2(f2(γ3)).Since iVj(fj(γ3))=iVj(fj(γ1))− iVj(fj(γ2))for j=1,2,the equation(4.3)follows.

(b)Let γ be in C([a,b],Sp(H)).By Proposition 3.1(d),there is a path α ∈ Pτ(H)such that α(τ)= γ(a).Denote by∈ P2τ(H)the path defined by α followed by γ.Since iVj(fj)=iVj(fj(α))+iVj(fj(γ))for j=1,2,the equation(4.4)follows.

(c)Let γ ∈ C([0,1],Sp(H))be such that γ(0)= γ(1)=I.Then we have a homotopy h:[0,1]2→ Sp(H)such that h(s,t)=f1(γ)f2(γ).So we have[f1(γ)f2(γ)]=[f1(γ)]+[f2(γ)]in π1(Sp(H))and(c)follows.

4.2 The iteration formulae for the A-iteration of the symplectic path

Firstly,we define the iteration of a symplectic path γ ∈ Pτ(H).

Definition 4.1(see[12,(4.3)–(4.4)])Let(H,ω)be a symplectic Hilbert space defined in Section2.Given anA ∈ Sp(2n),aτ＞ 0,a positive integerkand a pathγ ∈ Pτ(H),we define

(a)We callthek-thA-iteration ofγ.The mapPA(γ):=A−1γ(τ)is called the Poincar´e map ofγatτ.

(b)IfdimHisfinite,we define

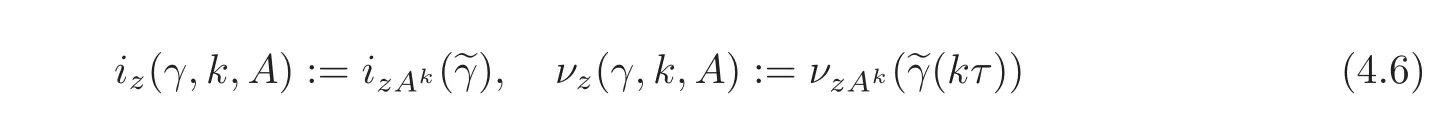
for eachz∈Cwith|z|=1.

We need the following lemmas.

Lemma 4.3LetXbe a vector space andA,B∈End(X)be two linear maps.Assume thatAB=BA.ThenABis Freholm if and only ifAandBare Fredholm.In this case we have

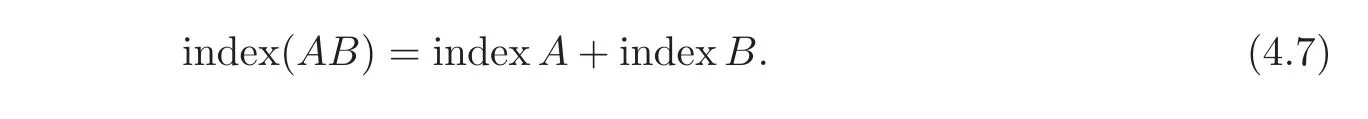
ProofIf A and B are Fredholm,AB is Fredholm and(4.7)holds.Since AB=BA,we have

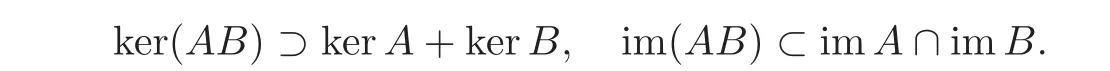
So A and B are Fredholm if AB is Fredholm.

The following fact is clear.

Lemma 4.4LetXandYbe two Abelian groups andA,B∈Hom(X,Y)be two group homomorphisms.Then we haveker(A−B)Gr(A)∩Gr(B)andY/im(A−B)(X×Y)/(Gr(A)+Gr(B)).

We have the following form of iteration formula.

Theorem 4.1(The Iteration Formula for the Power of the Symplectic Path)Let(H,ω)be a symplectic Hilbert space defined in Section2.Letγ ∈ C([a,b],Sp(H))be a symplectic path such that(γ(t))k− IHis Fredholm of index0for eacht∈ [a,b],wherekis a positive integer.Then we have

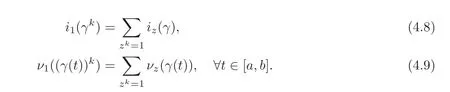
ProofSet Vj:=Grfor j=0,···,k.Recall that the integers i(γ)and

zνz(γ(t))are defined by Definition 2.1.It is clear that the equation(4.9)holds.By Lemmas 4.3–4.4,we can apply Theorem 2.2 and our result follows.

Let γ(t)be the path in Theorem 4.1.Since the zero operator 0 on H is not Fredholm if dimH=+∞,γ(t)can not be IHfor each t∈ [a,b]in this situation.

Our next result for periodic Hermitian systems was obtained by[3,Corollary of Theorem I]when A=zIHand|z|=1,in the real case was obtained by Y.Long[13,Theorem 1.4]when A=zIHand|z|=1,by X.Hu and S.Sun[9,Theorem 1.6]when A∈Sp(2n,R)∩U(2n),and by C.Liu and S.Tang[10,Theorem 1.1]when A∈Sp(2n,R).

Corollary 4.1(The Iteration Formula for the A-Iteration of the Symplectic Path)Let(H,ω)be afinite dimensional symplectic Hilbert space.Given anA ∈ Sp(H),aτ＞ 0,a positive integerkand a pathγ ∈ Pτ(H),we have

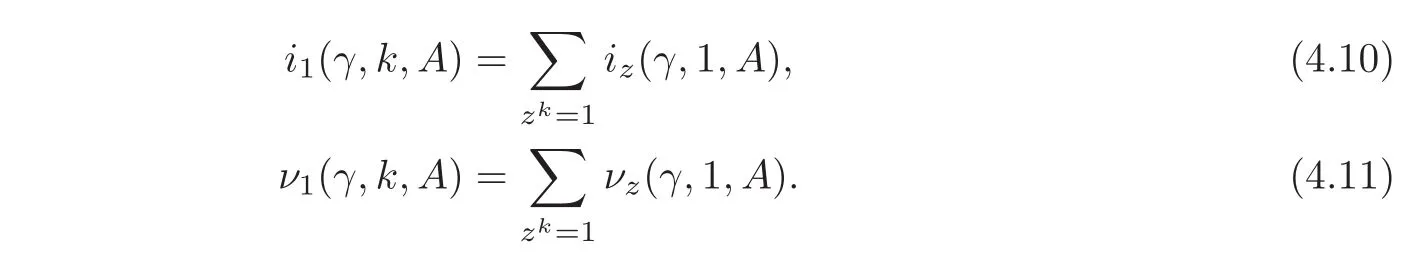
Moreover,there is a functionδk:Sp(H)→ Zdefined by

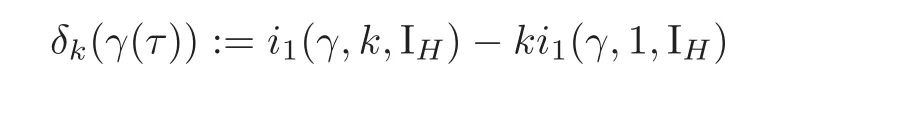
such that

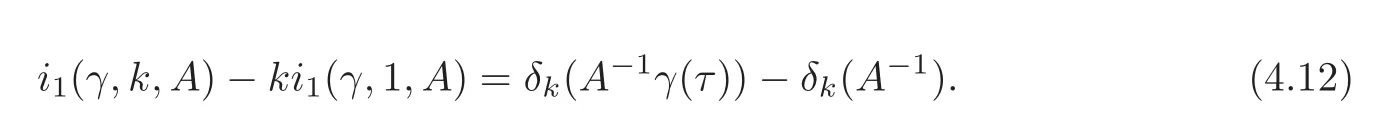
ProofNote that A−kγ(kτ)=(A−1γ(τ))k.By(2.11),Lemma 4.1 and Theorem 4.1,we obtain(4.10)and(4.11).By Lemma 4.2,the function δkis well-defined and(4.12)holds.

4.3 Two times iteration formula for the generalized brake symmetry

Firstly,we define the iteration of a symplectic path γ ∈ Pτ(H)for the brake symmetry.

Definition 4.2(see[12,(4.3)–(4.4)])Let(H,ω)be a symplectic Hilbert space defined in Section2.LetN ∈ B(2n)be such thatN∗JN= −JandN2=IH.Given aτ＞ 0,a positive integerkand a pathγ ∈ Pτ(H),we define

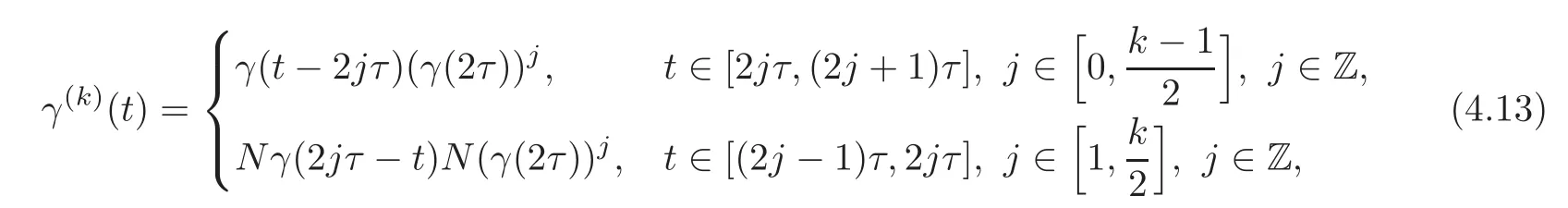
whereγ(2τ)=Nγ(τ)−1Nγ(τ).We callγ(k)thek-thN-brake iteration ofγ.The mapγ(2τ)is called the Poincar´e map ofγat2τ.

We have the following algebraic results.

Lemma 4.5LetX,Ybe two linear spaces with decompositionsX=V1⊕V2andY=W1⊕W2respectively.LetM∈Hom(X,Y)be of the form

Proof(4.14)is clear,(4.15)follows from direct calculation,and(4.16)follows from(4.14)–(4.15).

Lemma 4.6LetXbe an Abelian group such that2IXis an isomorphism onX.LetM,N,S∈End(X)be three endmorhpisms onXsuch thatMis an isomorphsim andN2=

(NS)2=IX.SetU±:=ker(N∓IX),V±:=ker(NS∓IX),andK:=NM−1NM.LetMbe in the form

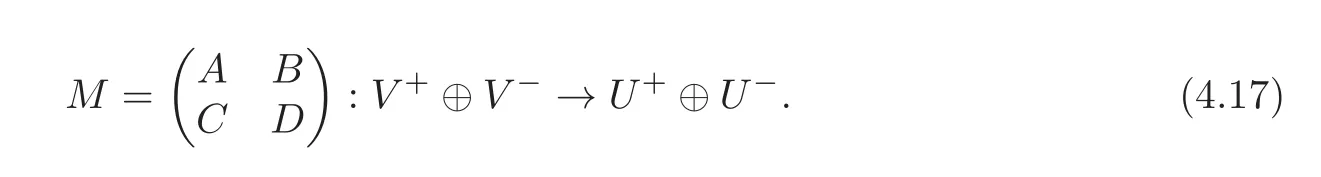
Then we have

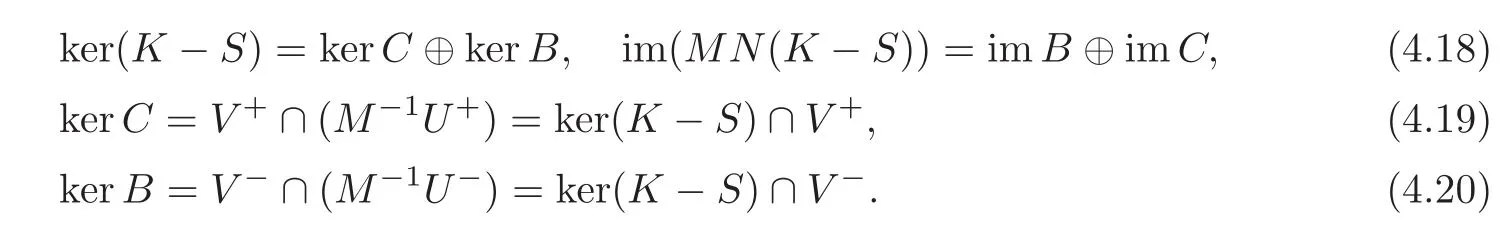
ProofSince(NS)2=IX,we have

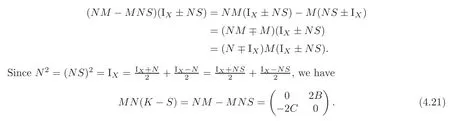
Our results then follows from(4.21)and direct computations.

Lemma 4.7Let(H,ω)be a symplectic Hilbert space defined in Section2.LetN ∈ B(H)be a bounded opertor such thatN∗JN= −JandN2=IH.Letγ ∈ C([a,b],Sp(H))be a positive symplectic path.Then we haveN∗J= −JN,and the pathα :=Nγ−1Nis a positive symplectic path.

ProofSince N∗JN= −J and N2=IH,we have N∗J= −JN−1= −JN.Since γ is a symplectic path,α is also a symplectic path.It follows that

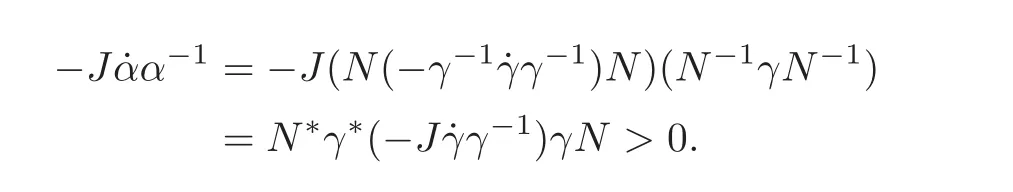
The proof is complete.

We have the following form of two times iteration formula for the generalized brake symmetry.

Theorem 4.2Let(H,ω)be a symplectic Hilbert space defined in Section2.LetN ∈ B(H)be a bounded opertor such thatN∗JN= −JandN2=IH.LetS ∈ Sp(H)be such that(NS)2=IH.Letγ ∈ C([a,b],Sp(2n,H))be a symplectic path such thatNγ(t)−1Nγ(t)− Sis Fredholm of index0for eacht∈[a,b].Then we have

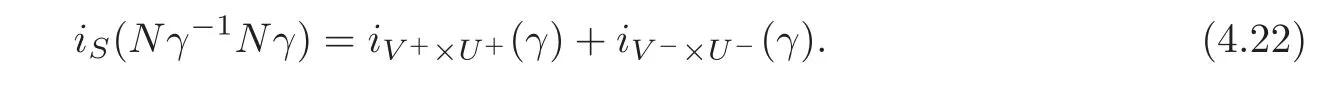
ProofSet V0:=Gr(S),V1:=V+×U+,V2:=V−×U−.By Lemmas 4.5–4.6,we have

for each t∈ [a,b].By[2,Proposition 1],we have index(Gr(γ(t)),Vj)≤ 0 for j=1,2.So both of the two index are 0.By Lemmas 4.5–4.7,we can apply Theorem 2.2 and our result follows.

Our next result in the real case was obtained by Y.Long,D.Zhang and the second author[15,Proposition C]when S=IH,and by X.Hu and S.Sun[9,Theorem 1.6]when S,N∈Sp(2n,R)∩U(2n).

Corollary 4.2(Two Times Iteration Formula for the Generalized Brake Symmetry)Let(H,ω)be a complex symplectic Hilbert space of dimension2n.LetN ∈ B(H)be a bounded operator such thatN∗JN=−JandN2=IH.LetS∈Sp(H)be such that(NS)2=IH.Given a pathγ ∈ Pτ(H),we have

ProofBy Lemma 4.1 and Theorem 4.2,the result follows.

4.4 The iteration formula for the brake symmetry

Let(H,ω)be a symplectic Hilbert space defined in Section 2.Let N ∈ B(H)be such that N2=IHand N∗JN= −J.Set U±:=ker(N ∓IH).Then we have U±∈L(H).By replacing the inner product of H with 〈·,·〉U−⊕ 〈·,·〉U+,we can assume that N∗N=IH.Here the form ω is unchanged.Wefix the orthogonal decomposition H=U−⊕U+.Then we havewhere K ∈B(U−,U+)and K,K∗are injective maps.

Lemma 4.8LetXbe a vector space with two linear mapsA,B∈End(X).Assume that one of the following three conditions holds:

(i)ker(AB)⊃kerA,andB:kerA→kerAis surjective.

(ii)ker(AB)⊃kerA,kerA∩kerB={0},andkerAisfinite dimensional.

(iii)kerAandkerBarefinite dimensional,anddimker(AB)≥dimkerA+dimkerB.

Then there exist short exact sequences

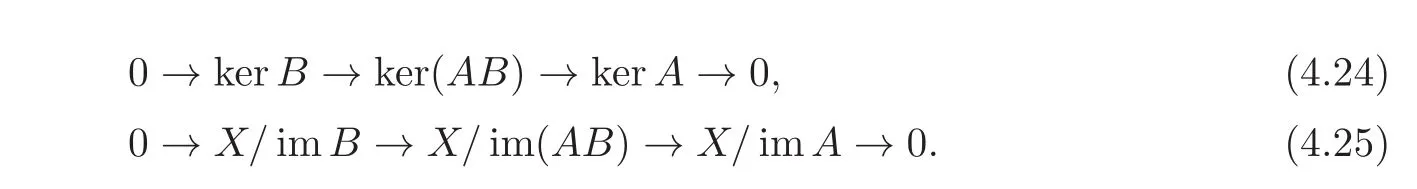
ProofBy[18,Exercises B.11],it is enough to show that B:ker(AB)→kerA is surjective.(i)Since ker(AB)⊃kerA,we have

Since B:kerA→kerA is surjective,we have B ker(AB)⊃B kerA=kerA.So we obtain B ker(AB)=kerA.Thus B:ker(AB)→kerA is surjective and our results follow.

(ii)Since kerA∩kerB={0},the map B:kerA→kerA is an injection.Since dimkerA＜+∞,it is an isomorphism.By(i),our results hold.

(iii)By[18,Exercises B.11],we have dimker(AB)≤dimkerA+dimkerB.So we have dimker(AB)=dimkerA+dimkerB＜+∞.By[18,Exercises B.11],B:ker(AB)→kerA is an isomorphism.So(4.24)and(4.25)hold.

Lemma 4.9LetM=∈Sp(H)be such that(NM)2=IHandkbe a positiveinteger.Then the following hold:

(a)(see[6,Proposition 2.1])We have

(b)Letαbe a real number such that/∈Z.Then we have

(c)(see[6,Lemma 3.1])Denote byTkandUkthe Chebyshev polynomials of thefirst kind and the second kind respectively.Then we have

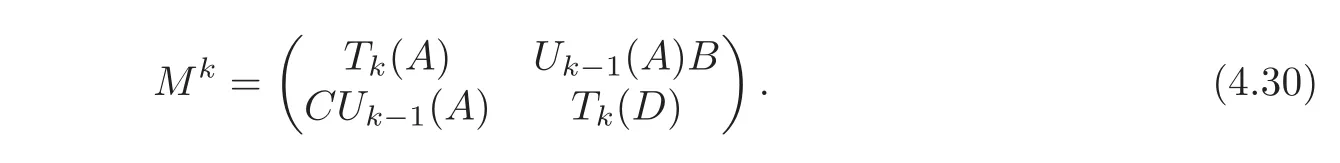
(d)Assume that there isP ∈Sp(H)such thatM=NP−1NP.Then the pair(Gr(M),U+×U+)is Fredholm(of index0)if(Gr(P),U+×U+)and(Gr(P),U+×U−)are Fredholm(of index0).In this case,we have

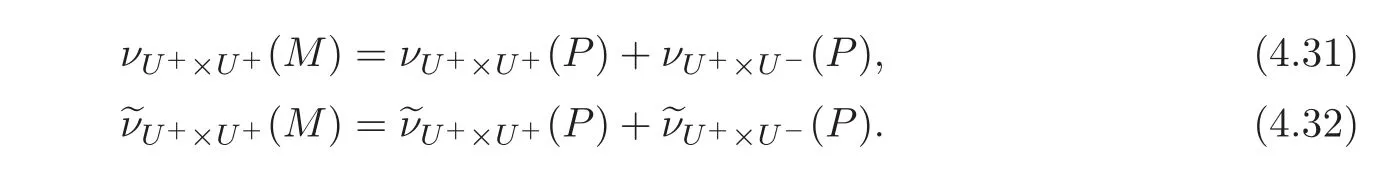
(e)Thepair(Gr(Mk),U+×U+)is Fredholm(of index0)if and only if(Gr(M),U+×U+)andM−Iare Fredholm(of index0)forj=1,···,k − 1.In this case,we haveH

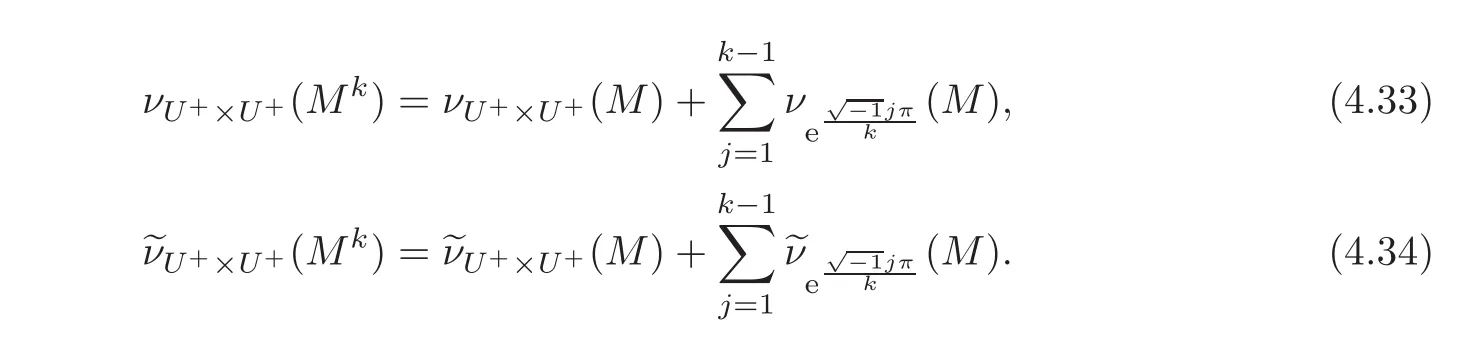
(f)Assume that there isP ∈Sp(H)such thatM=NP−1NP.Then the pair(Gr(PMk),U+×U+)is Fredholm(of index0)if and only if(Gr(P),U+×U+)andM−

IHare Fredholm(of index0)forj=1,···,k.In this case,we have

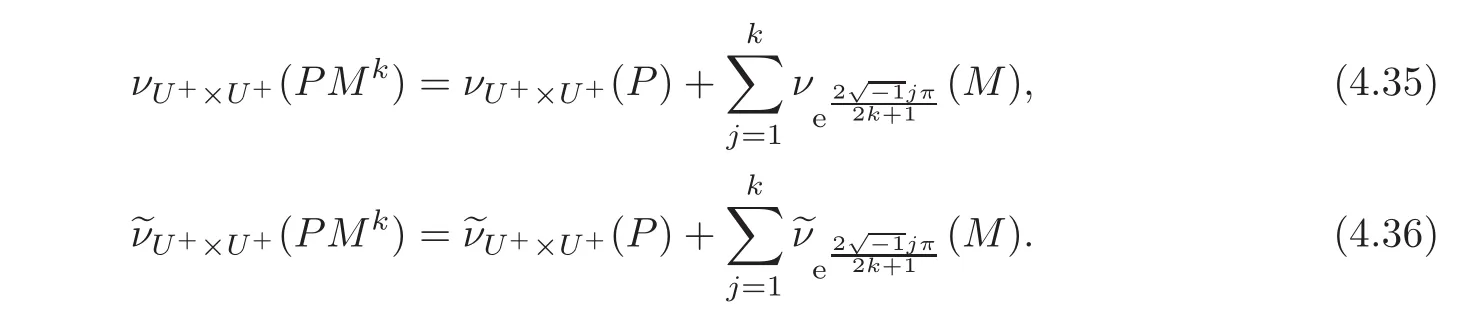
Proof(a)Since M is symplectic,we have

Since M∗JM=J and(NM)2=IH,we have M∗J=JM−1=JNMN.Then(4.26)holds.Then we have

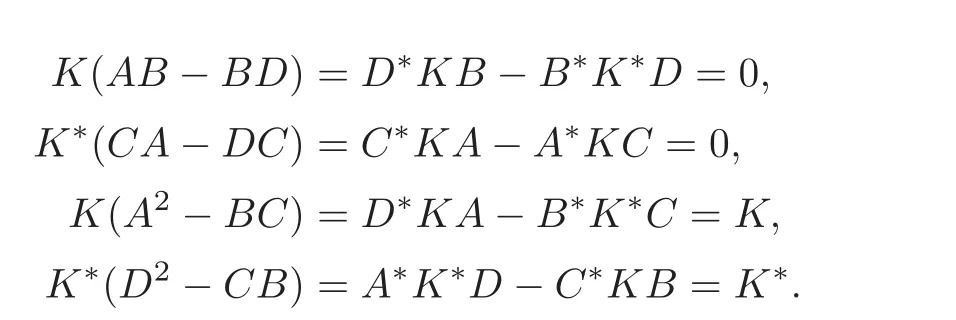
By the injectivity of K and K∗,we obtain(4.27).

(b)Set λ :=e−1α.Since(NM)2=IH,we have(MN)2=IHand λIH−MN is invertible.

Then we have

(c)In a similar way to the proof of[6,Proposition 2.1],where we replace ATby D,the result follows.

(d)Let P be of the form

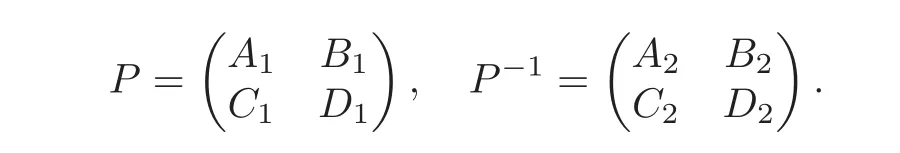
Then we have B=2A2B1=−2B2D1,and kerB1∩kerD1={0}.So we have

By a direct calculation,we have

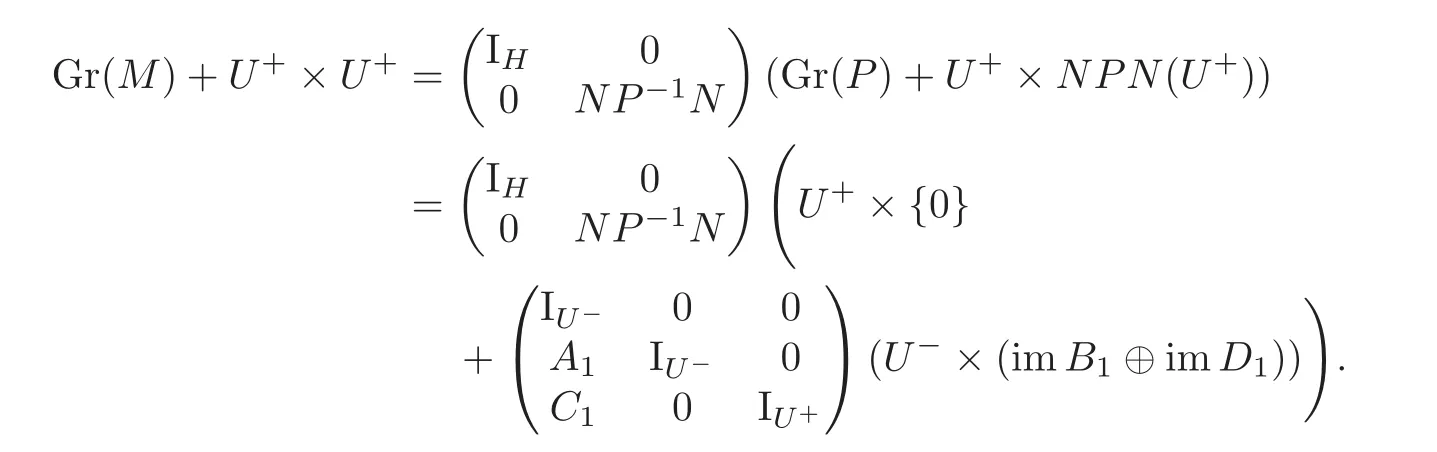
By Lemma 4.5,we have

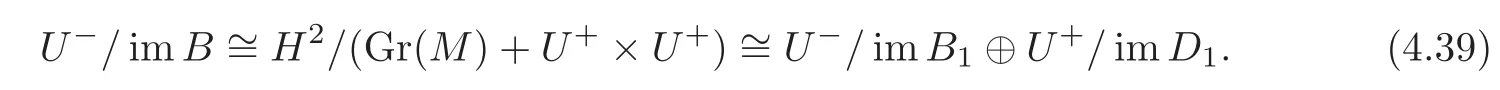
By(4.38)–(4.39),B is Fredholm if and only if B1and D1are Fredholm.In this case,we have

By Lemma 4.5 and(2.12),we have indexB1=index(Gr(P),U×U)≤0,indexD1=index(Gr(P),U+×U−)≤0 and indexB=index(Gr(M),U+×U+)≤0.So our result follows from(4.40)–(4.42).

(e)We have ker(Uk−1(A)B)⊃ kerB.Since AB=BD and Uk−1is a polynomial,we have Uk−1(A)B=BUk−1(D).It follows that ker(Uk−1(A)B)⊃ kerUk−1(D).

We recall the identities of Chebyshev polynomials(see[6,Lemma 4.1])for a∈C,

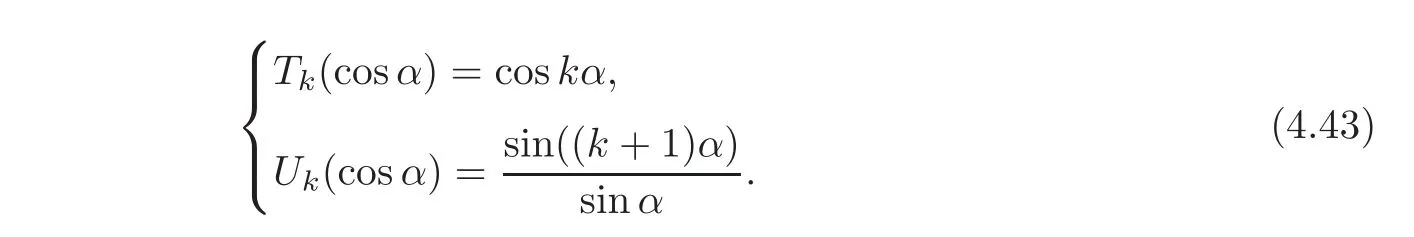
It follows that the set of zeros of Uk−1is{cos()|0＜j＜k,j∈Z}.Then we have

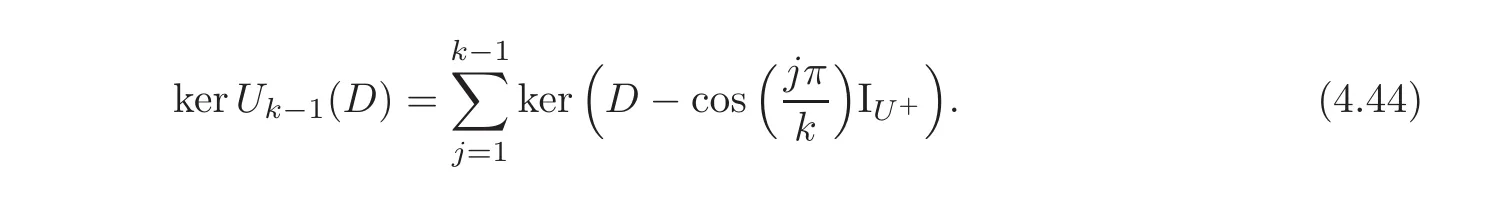
By(4.27),we have D2−In=CB.It follows that

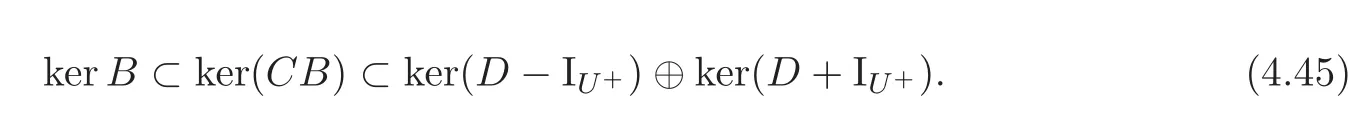
Then we can conclude that

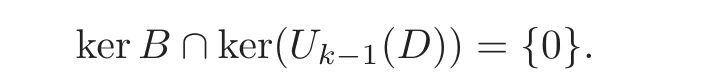
By Lem ma 4.8 and(b),(Gr(Mk),U+×U+)is Fredholm if and only if(Gr(M),U+×U+)andIHare Fredholm for k=1,···,k − 1.In this case(4.33)–(4.34)hold.By(2.12),(Gr(Mk),U+×U+)is Fredholm of index 0 if and only if(Gr(M),U+×U+)andare Fredholm of index 0 for k=1,···,k − 1.(f)Let P and PMkbe of the form

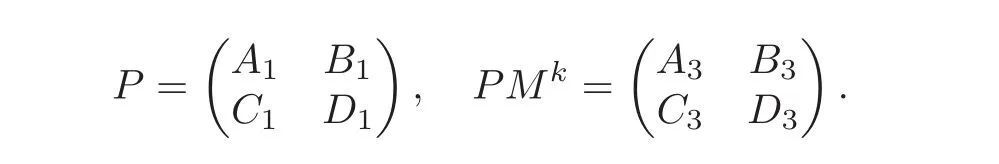
Since M=NP−1NP,we have PNM=NP.So A1B=B1(D+IU+)holds.Note that AB=BD.By(c),we have

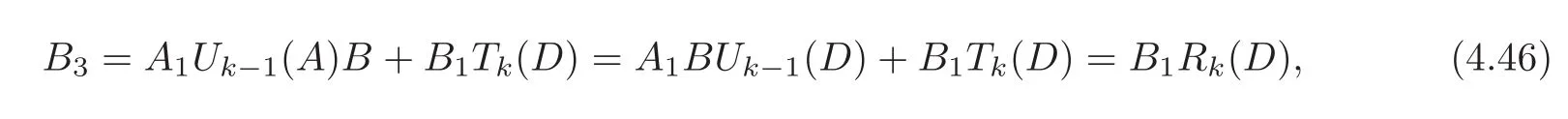
where Rk(x):=(x+1)Uk−1(x)+Tk(x)is a k-th order polynomial.By(4.43),we have

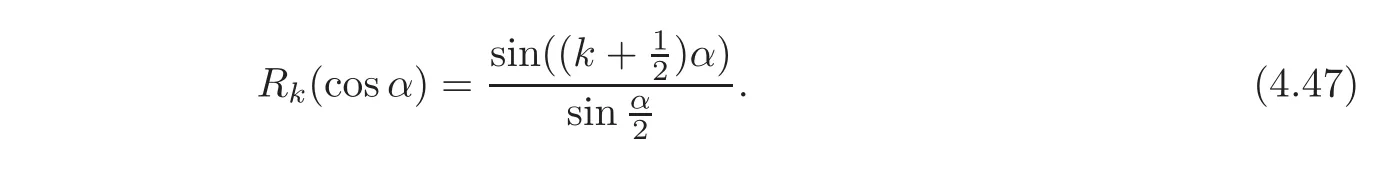
So the set of zeros of Rkis|1≤ j≤ k,j∈Z}.Since M=NP−1NP and NU+=U+,we have PU+∩U+⊂MU+∩PMkU+∩U+.So we have kerB1⊂kerB∩kerB3.By a proof similar to that of(e),(f)is obtained.

We have the following form of iteration formula for the brake symmetry.

Theorem 4.3Let(H,ω)be a symplectic Hilbert space defined in Section2.LetN ∈ B(H)be a bounded opertor such thatN∗JN= −JandN2=IH.Letγ ∈ C([a,b],Sp(H))be a symplectic path such that(Nγ(t))2=IH.SetU±:=ker(N∓IH).Letkbe a positive integer.Then the following hold:

(a)Assume that there is a symplectic pathγ1∈ C([a,b],Sp(H))such thatγ =NNγ1and the pair(γ(t)U+,U+)is Fredholm of index0for eacht∈ [a,b].Then we have

(b)Assume that the pair(γ(t)kU+,U+)is Fredholm of index0for eacht∈ [a,b].Then we have

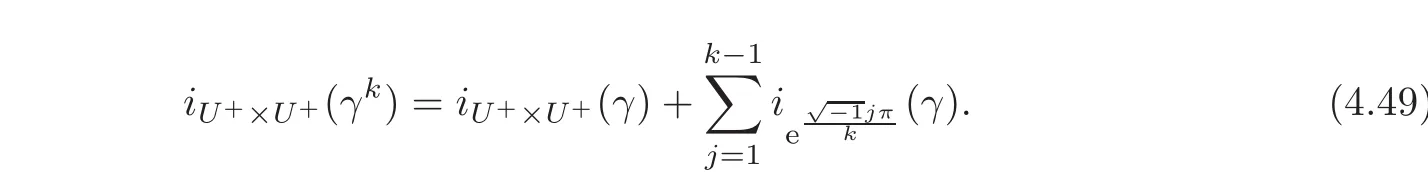
(c)Assume that there is a symplectic pathγ1∈ C([a,b],Sp(H))such thatγ =NNγ1and the pair(γ1(t)γ(t)kU+,U+)is Fredholm of index0for eacht∈ [a,b].Then we have

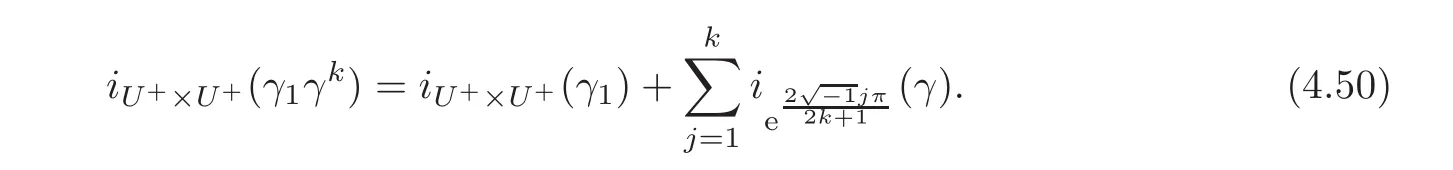
ProofNote that we can assume N∗N=IH.By Lemma 4.9,we can apply Theorem 2.2 and our result follows.

Our next result in the real case was obtained by[12,Theorem 1.3].

Corollary 4.3(The Iteration Formula for the Brake Symmetry)Let(H,ω)be a complex symplectic Hilbert space of dimension2n.LetN∈B(H)be a bounded opertor such thatN∗JN= −JandN2=IH.Letkbe a positive integer.Given a pathγ ∈ Pτ(H),the following hold:

(a)We have

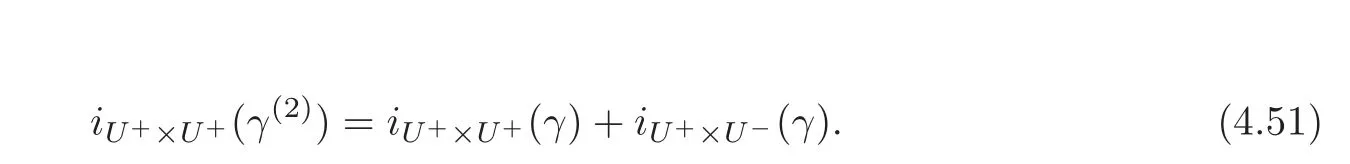
(b)Assume that(Nγ(τ))2=IH.Denote bythek-thIH-iteration ofγ.We have

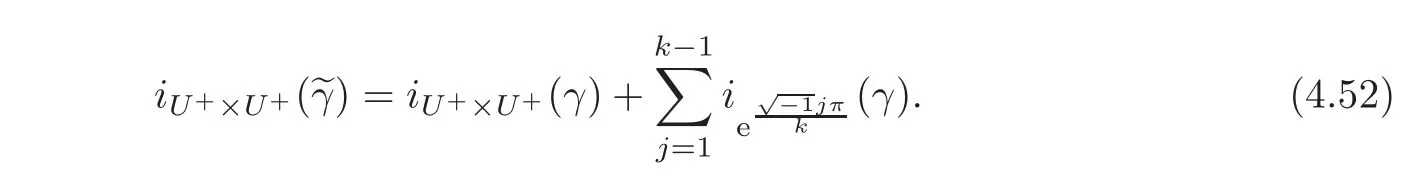
(c)We have

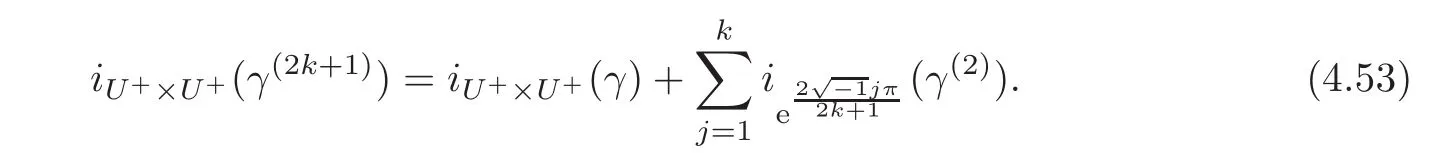
ProofBy Lemma 4.1 and Theorem 4.3,the result follows.

AcknowledgementThe authors would like to thank the referees for their critical reading and very helpful comments and suggestions.

[1]Booß-Bavnbek,B.and Zhu,C.,Maslov index in symplectic Banach spaces,Mem.Amer.Math.Soc.,to appear.arXiv:math/1406.1569v4[math.SG]

[2]Booß-Bavnbek,B.and Zhu,C.,The Maslov index in weak symplectic functional analysis,Ann.Global.Anal.Geom.,44,2013,283–318.

[3]Bott,R.,On the iteration of closed geodesics and the Sturm intersection theory,Comm.Pure Appl.Math.,9,1956,171–206.

[4]Duistermaat,J.J.,On the Morse index in variational calculus,Advances in Math.,21(2),1976,173–195.

[5]Ekeland,I.,Convexity Methods in Hamiltonian Mechanics,Ergebnisse der Mathematik und ihrer Grenzgebiete(3)(Results in Mathematics and Related Areas(3)),Vol.19,Springer-Verlag,Berlin,1990.

[6]Frauenfelder,U.and van Koert,O.,The Hö rmander index of symmetric periodic orbits,Geom.Dedicata,168,2014,197–205.

[7]Ginzburg,V.L.,The Conley conjecture,Ann.of Math.(2),172(2),2010,1127–1180.

[8]Hingston,N.,Subharmonic solutions of Hamiltonian equations on tori,Ann.of Math.(2),170(2),2009,529–560.

[9]Hu,X.and Sun,S.,Index and stability of symmetric periodic orbits in Hamiltonian systems with application to figure-eight orbit,Comm.Math.Phys.,290(2),2009,737–777.

[10]Liu,C.and Tang,S.,Maslov(P,ω)theory for symplectic paths,Adv.Nonlinear Stud.,15,2015,963–990.

[11]Liu,C.and Zhang,D.,Iteration theory of L-index and multiplicity of brake orbits,J.Differential Equations,257(4),2014,1194–1245.

[12]Liu,C.and Zhang,D.,Seifert conjecture in the even convex case,Comm.Pure Appl.Math.,67(10),2014,1563–1604.

[13]Long,Y.,Bott formula of the Maslov-type index theory,Pacific J.Math.,187(1),1999,113–149.

[14]Long,Y.,Index theory for symplectic paths with applications,Progress in Mathematics,Vol.207,Birkhäuser,Basel,2002.

[15]Long,Y.,Zhang,D.and Zhu,C.,Multiple brake orbits in bounded convex symmetric domains,Adv.Math.,203(2),2006,568–635.

[16]Long,Y.and Zhu,C.,Closed characteristics on compact convex hypersurfaces in R2n,Ann.of Math(2),155(2),2002,317–368.

[17]Salamon,D.and Zehnder,E.,Morse theory for periodic solutions of Hamiltonian systems and the Maslov index,Comm.Pure Appl.Math.,45(10),1992,1303–1360.

[18]Whitehead,G.W.,Elements of Homotopy Theory,Graduate Texts in Mathematics,61,Springer-Verlag,New York,Berlin,1978.

[19]Zhu,C.,A generalized Morse index theorem,Analysis,Geometry and Topology of Elliptic Operators,World Sci.Publ.,Hackensack,NJ,2006,493–540.