4WD/WS电动车辆稳定性分层控制与轮胎力优化分配算法研究*

孟腾飞，田晋跃，郑师虔

(江苏大学 汽车与交通学院， 江苏 镇江 212000)

0 引 言

目前，采用轮毂电机驱动/四轮线控转向控制电动车辆的形式引起了国内外的广泛关注。目前针对车辆稳定性的研究主要集中在主动转向控制和直接横摆力矩控制两个方面[1]。然而，这两类控制方式都有各自的缺陷。文献[2]设计了主动转向和直接横摆力矩的集成控制策略，该研究是基于前馈与反馈补偿的模型跟踪控制算法，对质心侧偏和车辆横摆角速度期望值进行跟踪，但是该算法没有充分考虑车辆各个运动之间的耦合关系，子系统不可避免的会产生相互冲突，另外车辆运动控制力均需要轮胎与地面接触产生，故轮胎力的控制精度直接影响车辆的整体性能；文献[3]提出一种轮胎优化分配算法，但是分配目标单一。

为了避免车辆解耦的难度，增加系统的灵活性，本研究将设计分层结构的集成控制算法，以实现整车目标运动到整车合力的转换，并设计带权重的分配目标函数，基于摩擦极限圆设计权重矩阵来控制分配，以优化各个车轮受力，提高车辆的行驶稳定性。

1 车辆动力学模型的建立

本文建立车辆动力学模型如图1所示。

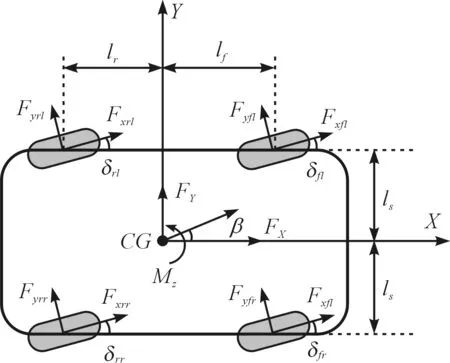
图1 车辆动力学模型

该模型主要考虑侧向运动、纵向运动和横摆运动，忽略侧倾运动、垂直运动、俯仰运动[4]，并且悬架机构的影响不予考虑。该模型包括4个车轮的转动、横向、纵向、横摆7个自由度。

根据牛顿动力学可以建立X，Y，Z方向的平衡方程：

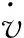
(1)

(2)

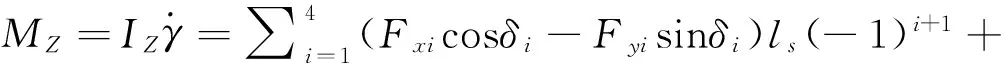
(3)

式中：Fxi，Fyi，δi—第i个车轮的纵向力、侧向力、转向角，i=1，2，3，4=fl，fr，rl，rr；lf，lr，ls—质心到各轴的距离；m—车辆质量；vx，vy—车辆纵向、侧向速度；γ，MZ—车辆横摆角速度与横摆力矩；β—车辆质心侧偏角。

2 集成控制结构

集成控制结构采用分层控制，上层包括信号处理层、力矩控制层，下层为控制分配层。信号处理层根据驾驶员的方向盘转角输入和油门踏板位置，利用参考模型计算出期望横摆角速度。力矩控制层决策出实现车辆稳定性控制所需的总侧向力、纵向力和横摆力矩。控制分配层根据所需的目标力矩对四轮驱动力和四轮转向角进行合理分配，最终通过执行相应电机实现车辆稳定性控制。该分层集成算法对四轮驱动、转角进行统一控制、分配，可以很好地避免了各个子系统之间的耦合影响，提高算法的准确性，提高子系统的发挥潜力。

集成控制结构框图如图2所示。

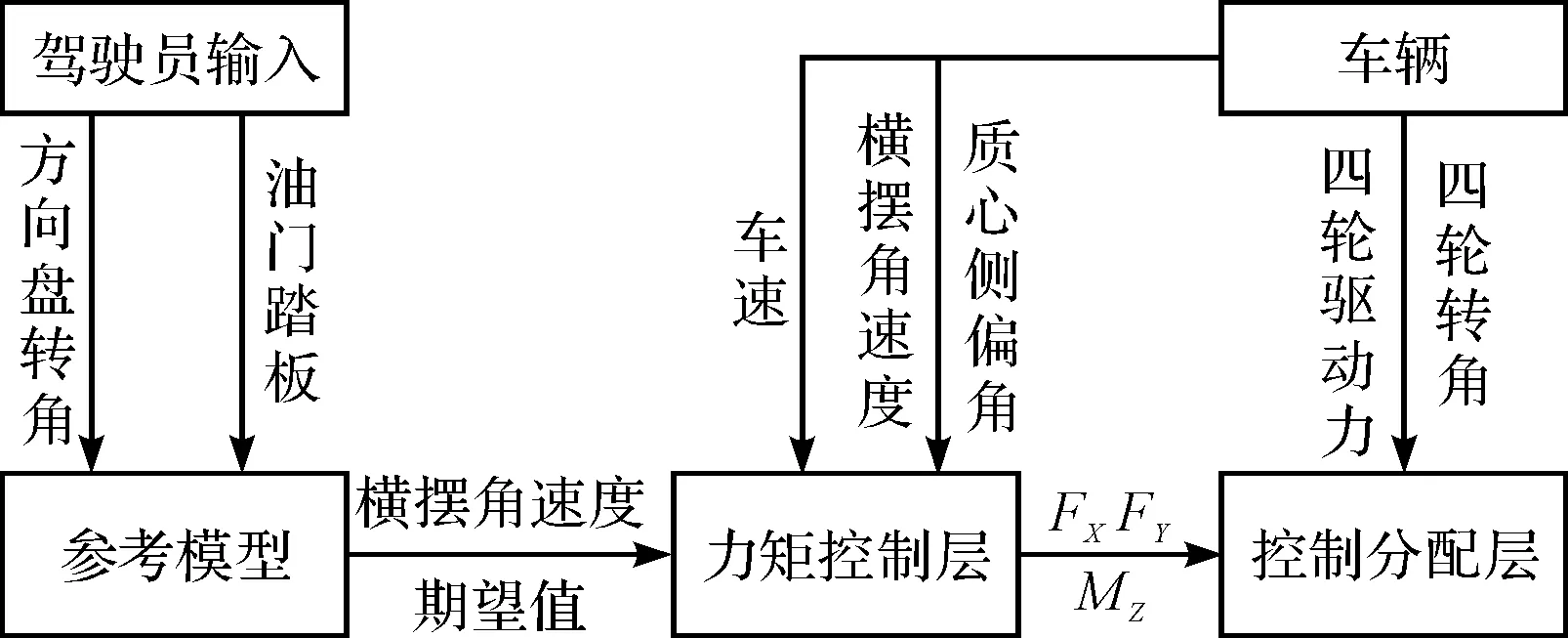
图2 集成控制结构框图

3 上层力矩控制算法设计

由于车辆模型不考虑车体的侧倾与俯仰，根据公式(1～3)可知:

(4)

3.1 控制目标

线性二自由度车辆模型不仅能够较好地反映车辆稳定行驶状态，而且实时性好，因此控制系统多选用其作为参考模型[5]。车辆理想的线性二自由度模型忽略了转向系统及悬架系统的影响，将车辆运动限制在平行于地面的平面内，并认为轮胎侧偏特性始终处于线性范围内，车辆质心侧偏角很小。因此可以根据线性二自由度车辆模型求得在一定方向盘转角与油门踏板下期望横摆角速度：

(5)

式中：γd—期望横摆角速度；k—稳定因子。

另外考虑质心侧偏角对稳定性的影响，当质心侧偏角增大时，汽车的横摆力矩随着侧偏角增加反而逐渐下降，直至降为零。质心侧偏角较小时，轮胎尚未进入非线性饱和区域，随着前轮转角增加，横摆力矩明显增加，驾驶员可以通过方向盘对车辆进行操纵，然而随着质心侧偏角的增大，由于轮胎的侧偏特性进入非线性饱和状态，侧偏力趋于饱和，横摆力矩也趋于不再变化，即此时车轮转角的改变已经不能产生横摆力矩，此时驾驶员通过操纵方向盘难以对车身的稳定性进行有效地维持，因此车辆稳定性控制的目标是保持质心侧偏角β越小越好，这里选取目标质心侧偏角为零，目标车身横摆角速度由上式(5)推导得到。

3.2 控制算法

滑模变结构控制(sliding mode control， SMC)在控制过程中控制量并不是连续变化的，所以说其实质上是一种特殊的非线性控制方式[6]。通常系统的状态(如偏差及其导数)是不断变化的，而该控制系统的结构则可以根据当前系统状态有规律地进行调整，从而将其状态轨迹约束在预定的区域内(被称为滑动模态)。由于滑动模态可以自行定义，且与系统对象的参数及外界扰动无关，使得该控制方式具有较好的鲁棒性。

对于一般系统：

(6)

存在一个切换面s(x)=0将该系统的状态空间分为s<0和s>0两个部分，在切换面上运动的点中有一类会在到达切换面s=0附近时向切换面进行趋近运动，这类运动点满足：

(7)

所以，进行滑模变结构控制其实就是要找到上述的切换面并设置相应的控制函数。

首先，假设某一控制系统：

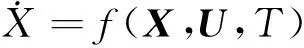
(8)

式中：X,U—系统的状态向量和控制向量，X∈Rn，U∈Rn；T—时间变量，T∈Rn；U—控制量，U=U(X，T)。

然后，确定切换面函数：

s(x，t)=0s∈Rn

(9)

最后，求解控制函数：

(10)

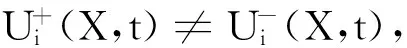
3.3 控制策略

根据稳态质心侧偏角相图和横摆角速度相图可定义滑模函数为：

(11)

(12)

(13)

式中：Cr，Cβ，Cu—滑模常数，满足赫尔维茨条件，即Cr>0，Cβ>0，Cu>0；ud—目标车速；eβ—车辆实际质心侧偏角与理想质心侧偏角的偏差；er—车辆实际横摆角速度与理想角速度的偏差；eu—实际车速与驾驶员目标车速的偏差。

为了保证实际跟踪误差轨迹限制在跟踪误差滑模面上，且系统渐近稳定，定义Lyapunov函数为V=S2/2，采用指数趋近[7]：

(14)

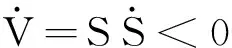
根据式(4，12～14)可求得所需施加到车辆上的总侧向力、纵向力与横摆力矩：

(15)

4 下层控制分配算法研究

4.1 轮胎稳定性分析

由上一节(上层控制层)可以求出在一定工况和对应行驶状态下车辆所需施加的总纵向力、侧向力和横摆力矩，这些力与力矩是每个轮胎滑移和侧偏的综合作用效果[8]。因此，为了实现对车辆目标运动的控制，需要将轮胎力分配到各个车轮上，再由相应的执行器(车轮转向电机、驱动电机、制动盘)对轮胎力进行精确控制从而完成车辆运动目标的控制。在控制的过程中主要有两个控制目标：(1)确保车辆的稳定性；(2)保证车辆动力性能。另外评价车辆的稳定性参数有很多。如：横摆角速度、质心侧偏角、车辆滑移率。然而，从基本轮胎动力学的观点来看，轮胎附着裕度可以很好地反映车辆运动的稳定性，车辆各个轮胎力应该尽量远离轮胎的极限边界[9]。为了描述单个轮胎的工作状态，轮胎的附着裕度可以定义为：

(16)

式中：Fzi—i车轮的垂直载荷。

轮胎附着裕度表述了实际轮胎力与摩擦圆边界的接近程度。它的取值范围为0≤ε≤1，当ε接近1时，表明轮胎的利用率很小，车辆较为稳定；当ε接近0时，表明轮胎力的利用率已接近极限，轮胎处于打滑的临界状态或者已经完全打滑[10]。

4.2 控制算法分析

设计目标函数：

J3=J1+J2

(17)

其中：

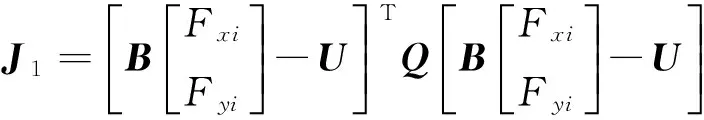
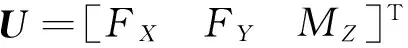
B如下式所示：

(18)

其中：

Q为J1权重系数矩阵：

Q=diag(q1，q2，q3)

(19)

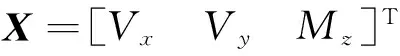
W为J2的权重系数矩阵：

(20)

其中：

W1=diag{(-lgwx1)k1，…，(-lgwx4)k1}
W2=diag{(-lgwy1)k2，…，(-lgwy4)k2}

从轮胎力学来看这里的wx1，wy1是车辆在某一运动状态下，横向力与纵向力方向上到轮胎摩擦圆边界的距离，轮胎摩擦圆如图3所示。

图3 轮胎摩擦圆

因此wx1，wy1可由下式计算得到：

(21)

值得注意的是，矩阵W对角线的元素是随着wx1，wy1负对角变换的，该变化曲线如图4所示。

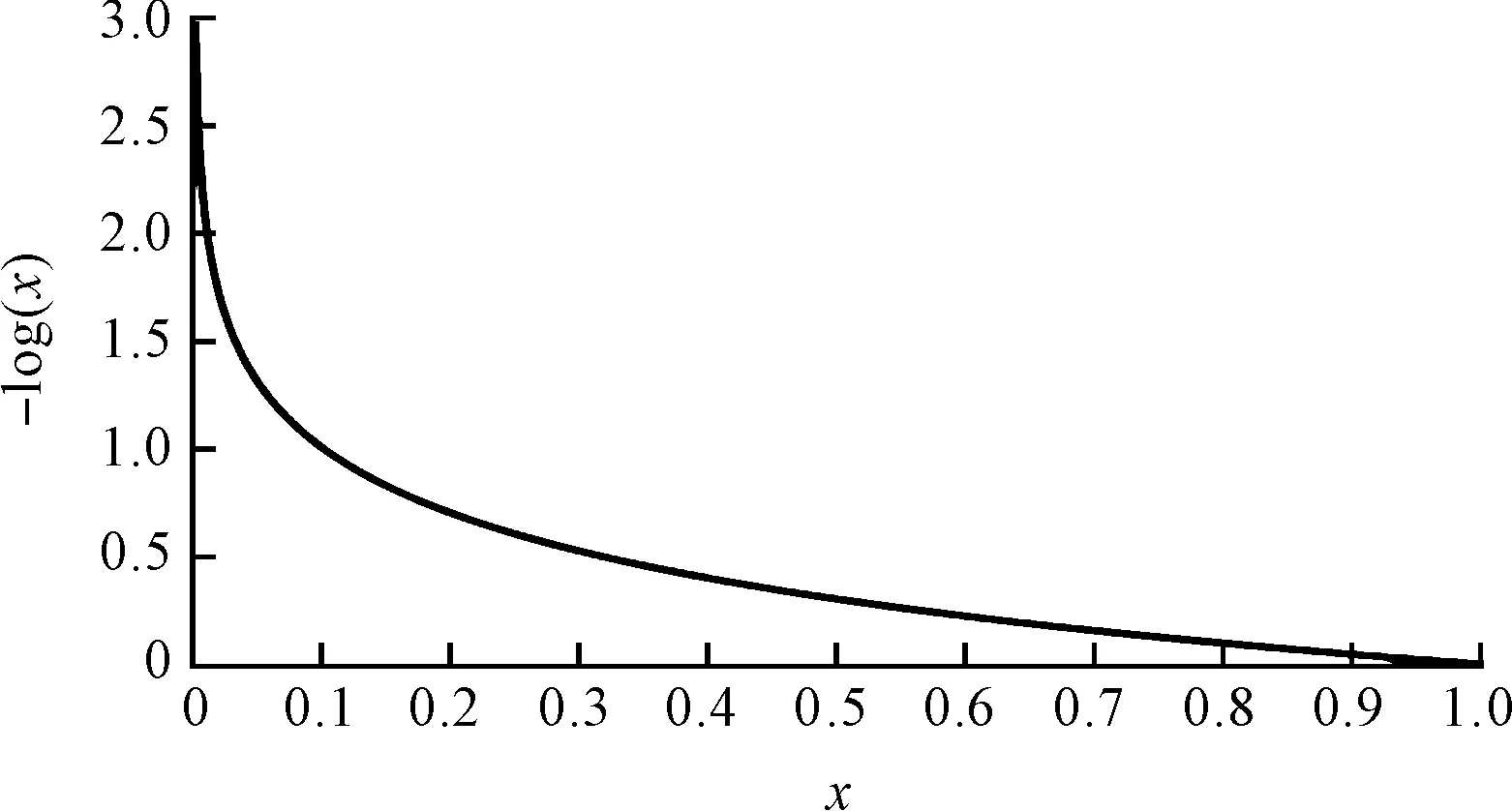
图4 -lg(x)随x变化曲线

当任何一个轮胎的纵向或横向力将要超过轮胎摩擦圆时(相应轮胎的或近似为零)，权重系数将急剧增加，这将有效地限制轮胎的滑动和侧向运动，进而保持了车辆稳定行驶。另外，当轮胎力远离摩擦圆时，即wx1或wy1远大于零，该函数可以降低来自下层控制器对轮胎的抑制，保证了非极端情况下车辆的动态性能。另外式(20)中参数k的存在是为了进一步提高设计的灵活性，为随后的各种控制目标奠定基础。在后面的仿真部分中ki选择0.1。

4.3 控制算法的求解

目标函数为：

J3=[BF-U]TQ[BF-U]+FTWF

(22)

式中：F=[Fx1Fx2Fx3Fx4Fy1Fy2Fy3Fy4]T。

对目标函数求二阶导数为：

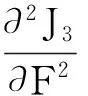
(23)

因此当一阶导数为零时可以求出目标函数的最小值：

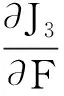
(24)

可以求得：

F*=(BTQB+W)-1BTQU

(25)

式中：F*—目标函数最小值时的每个车轮的纵向力与侧向力。

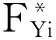
(26)

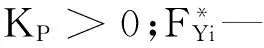
值得注意的是，δi可由式(26)求得，另外代入式(18)求得B矩阵，最终可以通过等式(25)求解得到期望轮胎力。

5 仿真验证

为了验证上述算法的有效性，即4WD/4WS车辆对目标纵向速度、侧向速度、横摆角速度的跟踪效果，与力分配层控制四轮轮胎附着裕度的能力，本文选用低附着路面的阶跃转向工况，建立Carsim/Simulink联合仿真实验[11]。

仿真工况设定为：车辆以120 km/h的车速在低附着路面(路面附着系数μ=4)上匀速直线行驶，在第2 s时刻驾驶员施加方向盘阶跃转角。

车辆纵向速度、侧向速度随时间变化曲线如图(5，6)所示。

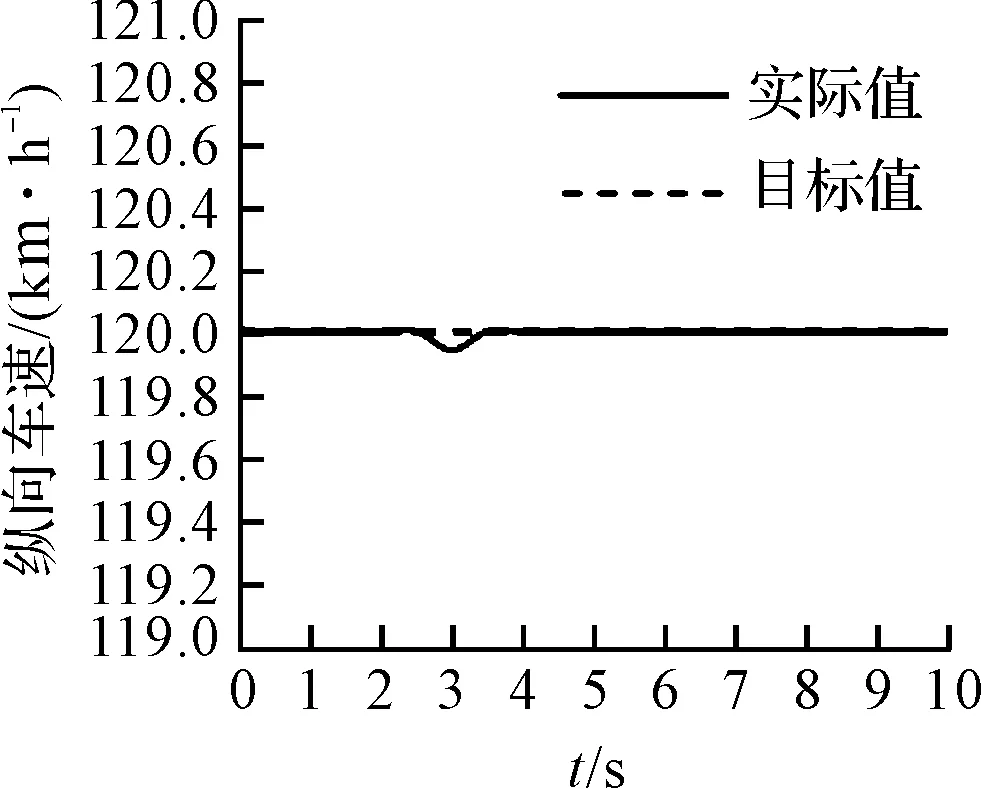
图5 纵向速度响应曲线

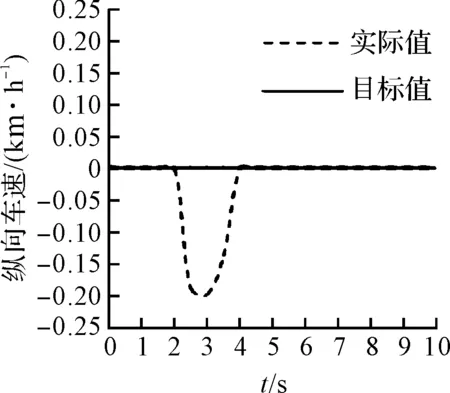
图6 侧向速度响应曲线

从仿真结果可以看出，在每个方向上的速度变化基本平稳，在阶跃转向瞬间只有小幅波动，车辆侧向最大速度约为0.20 m/s，之后均稳定为零，车辆纵向速度基本维持在120 km/h。由此可见该分层集成控制算法能够很好的保证驾驶员的舒适性，具有很强的鲁棒性。

四轮转向角度响应曲线如图(7，8)所示。

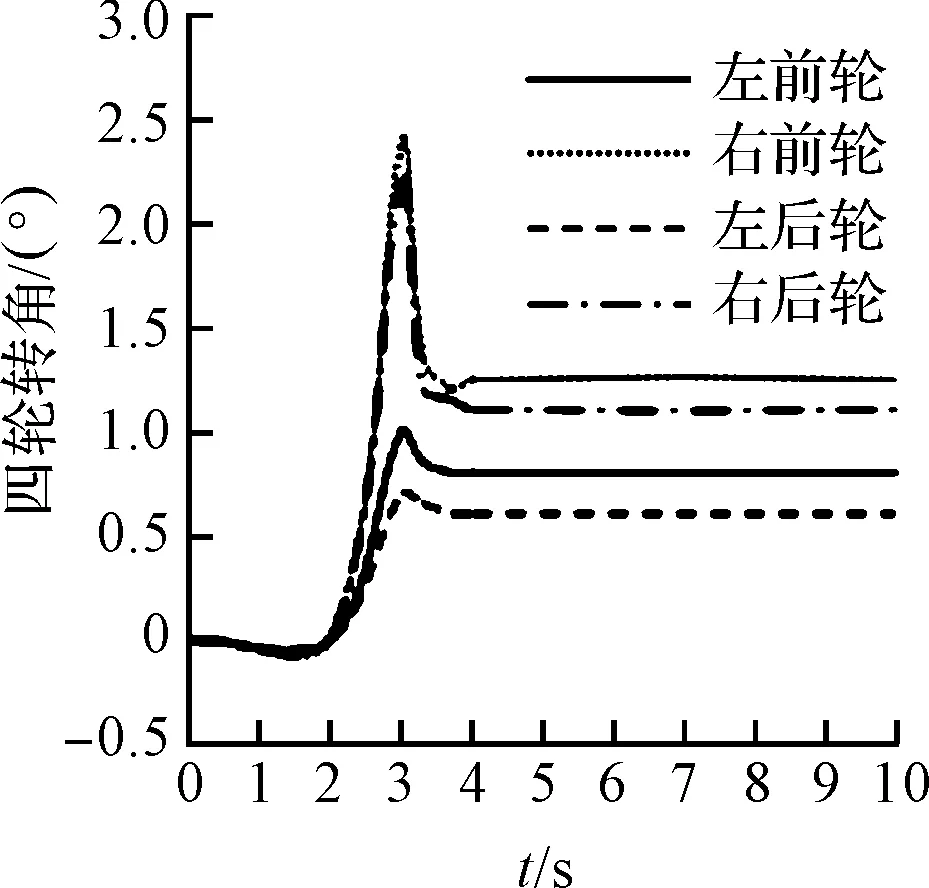
图7 四轮转向角度响应曲线

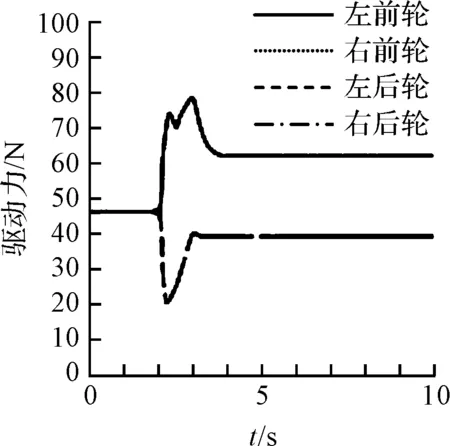
图8 四轮驱动力响应曲线

车辆在直线行驶时，各个车轮驱动力基本一致，四轮转角保持零度，另外整车车速保持目标车速，从而证实了上层控制算法(滑模变结构)可以准确的反映驾驶员意图。当车辆进入转向工况时，左侧轮和右侧轮由于垂直载荷转移造成的附着能力的变化较大，该控制算法可以用于快速地根据当前工况调整车辆各个车轮上的驱动力与转向角，从结果中不难看出各个车轮的驱动力与转向角进行了不同调整，充分反映了该分配算法能够很好地利用摩擦极限圆调整权重系数，合理的分配目标控制力，降低了在干扰因素作用下轮胎纵滑或侧滑的可能性，使车辆能很快地进入稳定状态。从而在保证轮胎稳定工作的前提下，保证了车辆转向所需的侧向力，纵向力，与横摆力矩。

横摆角速度响应曲线与质心侧偏角响应曲线如图(9，10)所示。

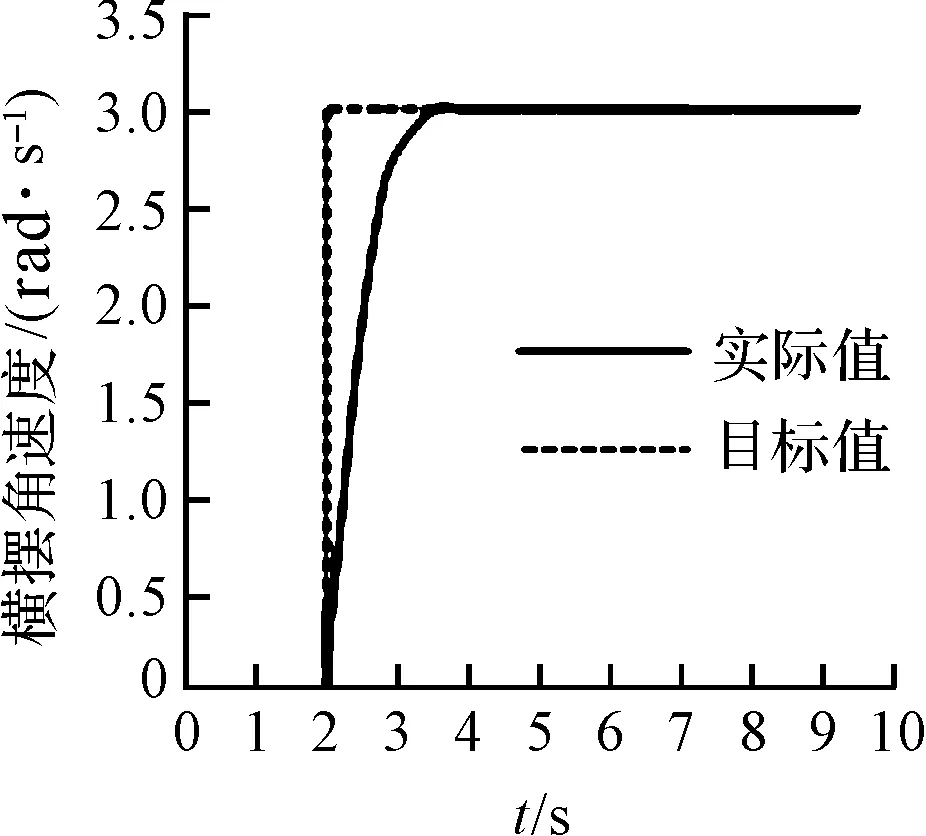
图9 横摆角速度响应曲线

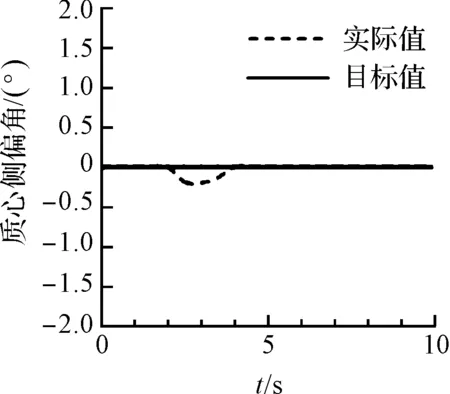
图10 质心侧偏角响应曲线

图中反映的是车辆横摆角速度与质心侧偏角随时间的变化情况，可以看出该分层式集成控制算法起到很好的控制效果。在仿真工况下，该控制算法在保证车辆零质心侧偏角的同时，对横摆角速度的跟踪效果也非常准确，从而整车的行驶稳定性得到保证。

6 结束语

为了克服车辆运动控制中各个子系统运动耦合，与力矩分配中分配目标单一的问题，本文设计了分层结构集成算法，力矩分配层中设计了带权重分配目标函数。

笔者利用Carsim/Simulink设计了仿真实验，仿真结果表明：该整车控制算法一方面实现了上层控制层对车辆总纵向力、总侧向力、总横摆力矩的需求，另一方面，分配层算法根据四车轮受力情况，合理分配了驱动力与转向角，从而保证了车辆的稳定行驶。

[1] ROSHAN N. Vehicle integrated controlan adaptive optimal approach to distribution of tire forces[C]. 2008 IEEE International Conference on Networking, Sensing and Control, Sanya: IEEE，2008.

[2] 马高峰.线控转向四轮轮毂电机电动汽车集成控制研究[D].锦州:辽宁工业大学机械工程与自动化学院，2016.

[3] EIICHI O, YOSHIKAZU H, YUJI M. Estimation of tire friction circle and vehicle dynamics integrated control for four-wheel distributed steering and four-wheel distributed traction/braking systems[J].R&DReviewofToyotaCRDL，2005，40(4):7-13.

[4] 余志生.汽车理论[M].4版.北京:机械工业出版社，2007.

[5] 石 晶，王 超，李 刚.四轮轮毂电机电动汽车横摆力矩变论域模糊控制研究[J].机械设计与制造，2015，16(4):166-177.

[6] LUO H, ZHANG L S, LAI F. Vehicle stability control system design using optimal allocation of yaw moment[J].JournalofChongqingUniversity，2010，33(10):19-24.

[7] 胡跃明，变结构控制理论与应用[M].北京:科学出版社，2002.

[8] 杨福广，阮久宏，李贻斌.4WID-4WIS汽车横摆运动AFS+ARS+DYC模糊控制[J].农业机械学报，2011，42(10):6-12.

[9] 张 聪，王振臣，程 菊.4WIS-4WID汽车横摆稳定性AFS+ARS+DYC滑模控制[J].汽车工程，2014，36(3):304-310.

[10] 柴 健，李旭宇，陈 刚.四轮独立驱动轮毂式电动汽车转向控制策略研究[J].公路与汽运，2014(5):1-5.

[11] NAM K, FUJIMOTO H, HORI Y. Design of an adaptive sliding mode controller for robust yaw stabilization of in wheel-motor-driven electric vehicles[J].InternationalJournalofVehicleDesign，2015，67(1):98-113.