一种惯性传感器与编码器相结合的AGV航迹推算系统*

吴 鹏，李东京，贠 超

(北京航空航天大学 机械工程及自动化学院，北京 100191)

0 引 言

自动导航车AGV是一种自动化无人驾驶的智能化搬运设备，是现代工业自动化物流系统中的关键设备[1-2]。其定位系统是实现自动导引的关键部分，也是目前的研究热点。定位是指AGV通过感知自身和周围环境信息，经过一定的数据处理得到自身位姿的过程。目前主要分为两类：绝对定位和相对定位[3]。

常用的绝对定位方式有全球定位系统(GPS)、超声波定位系统、红外网络系统、射频识别系统等等[4]。其中，GPS不能用在室内，并且更新频率较低[5]；超声波定位系统和红外网络系统具有低成本、小型化和易于连接的特点[6]，然而这两种方法不能在长距离下使用，同时需要在场景中大面积布置，并且由于信号干扰而难以满足AGV的定位要求[7]；而射频识别系统需要额外的设备和较高的成本[8]。这些绝对定位方法的优点在于它们不会积累定位误差，但整体定位误差较大[9]。

相对定位主要是指惯性导航和里程计算法(或测距法)[10]。惯性导航使用的主要传感器为IMU或AHRS，包括三轴的磁强计、三轴的陀螺仪和三轴的加速度计[11]。静止状态下，通过磁强计与加速度计获取姿态；运动状态下，通过加速度计获取位置，通过陀螺仪获取姿态。里程计算法使用的主要传感器为轮上编码器。运动状态下，基于主动轮上编码器的脉冲计数来估计AGV的位姿[12]。这两种相对定位方式都由于算法中引入了一次或二次积分而存在较大累积误差，单独使用时都很难保证AGV定位的准确性和稳定性[13]。

针对该问题，多数的研究采用将惯性导航与绝对定位相结合或里程计算法与绝对定位相结合的方式来消除累积误差。例如LU M F、LIU B C等人[14]将红外网络系统与里程计算法相结合；HELLMERS H、NORRDINE A等人[15]将超声波定位系统与惯性导航相结合；张永泽、艾长胜等人[16]将惯性导航与视觉相结合。但是这些研究都主要集中在使用外部信号来消除相对定位的累积误差上，并没有实质上减少里程计算法或者惯性导航算法本身所引入的累积误差。

本文将提出将惯性导航与里程计算法这两种相对定位算法相结合的方式，并搭建相应的实验平台对算法的有效性进行验证。

1 惯性导航

1.1 初始对准算法

惯性导航基于初始位置和初始姿态来计算AGV的相对位姿[17]。假设以起始点为原点，AGV的初始的姿态可以由相互正交的三轴加速度计和磁强计计算得出。

首先求出载体坐标系上的加速度向量：

(1)

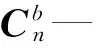
根据几何关系，φ，θ可由下面两式算出：

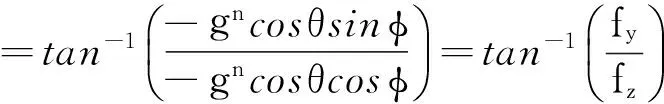
(2)

(3)

磁强计可以测量地球磁场在该地区的磁场强度在载体坐标系中的三轴分量，根据磁场强度可以计算得到偏航角φ。

地磁示意图如图1所示。

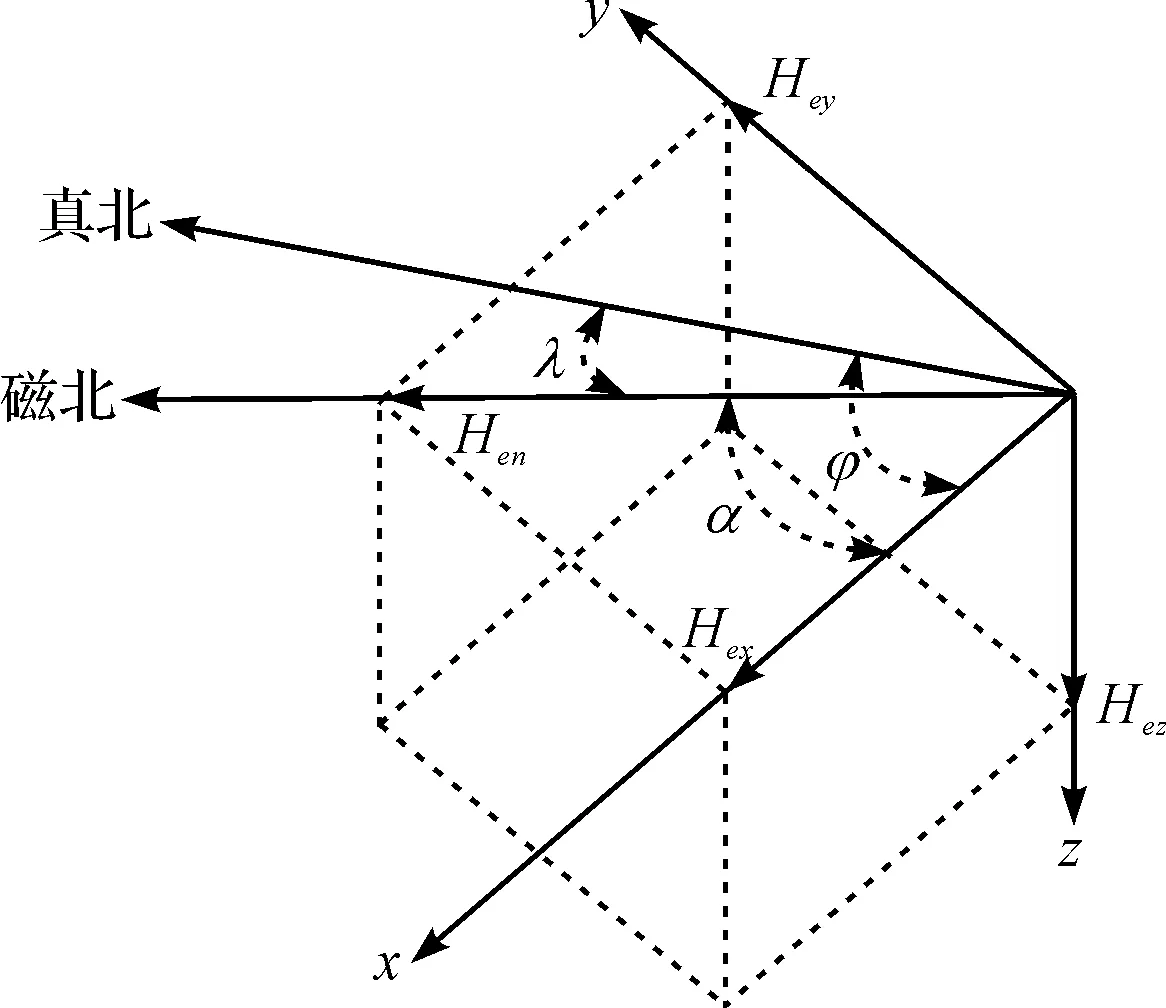
图1 地磁示意图

磁北角α由几何关系算出：

(4)

磁北和真北的差角为磁偏角λ，则偏航角为：

φ=λ+α

(5)

1.2 误差校准算法

当AGV运动时，可由三轴陀螺仪获取车身角速度在载体坐标系中的三轴分量，进而积分算得车身的姿态。同时，载体坐标系的速度和位置可分别由加速度的一次、二次积分算得。但是，该积分运算会使两传感器的误差随时间而累积，进而极大地影响速度和位姿的准确度。因此在将加速度计和陀螺仪用于AGV的定位时，必须通过校准和补偿来提高精度。

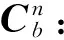
(6)

在静止状态下，加速度计所测得的加速度都来自于重力加速度，因此其在导航坐标系中的北向和东向的分量都为0，即这两个方向的测量值都是噪声：

(7)

(8)

求出加速度计噪声后，便可通过将其移除来获取估计值：

(9)

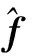
通过旋转矩阵将其表示在在载体坐标系中：

(10)

(11)

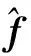
三轴陀螺仪提供角速度在载体坐标系中的三轴分量。当AGV静止时，陀螺仪在载体坐标系中的三轴分量应当都为0，因此此时的读数都是噪声：

(12)

(13)

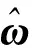
1.3 位置算法

速度和位置可分别由加速度的一次和二次积分算得：

vk+1=vk+fkΔt，Pk+1=Pk+vkΔt

(14)

代入加速度可得：

(15)

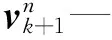
2 里程计算法

里程计算法使用的主要传感器为轮上编码器。运动状态下，基于主动轮上编码器的脉冲计数来估计AGV的位姿。

记编码器转一周产生的脉冲数为N，记测得的脉冲计数为M，则有：

(16)

式中：ηk，l，ηk，r—左右两轮的转角，以弧度为单位；Ml，Mr—两轮上编码器所测得的脉冲数。

里程计算法示意图如图2所示。

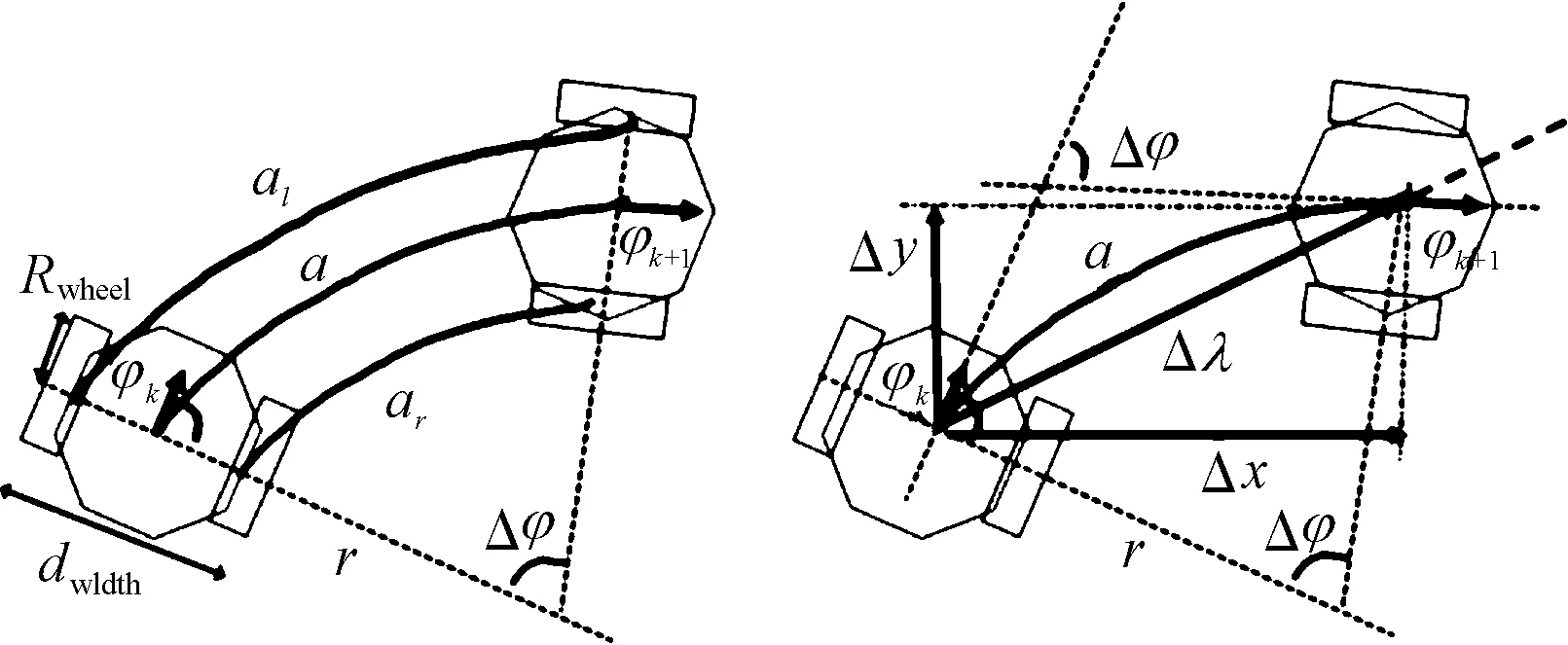
图2 里程计算法示意图

AGV的速度、位置和偏航角都可以基于两轮的转角ηk，l和ηk，r来计算。AGV的行驶距离ak可以用驱动轮的半径Rwheel，和轮子的转角来表示：

ak，l=Rwheelηk，l，ak，r=Rwheelηk，r

(17)

(18)

AGV的偏航角变化量Δφk，可以由AGV两驱动轮的间距和每个轮子的行驶距离来计算：

(19)

进而可以算得AGV车身的转动半径rk：

(20)

由余弦定理，AGV的位置变化量可以表示为：

(21)

当AGV作直线运动时，车身的偏航角变化量为0，此时计算得到的车身转动半径无穷大，上式中括号项为0，进而AGV的位置变化量为0，显然是不正确的。故单独处理这种情况，使用泰勒级数将式(21)展开：

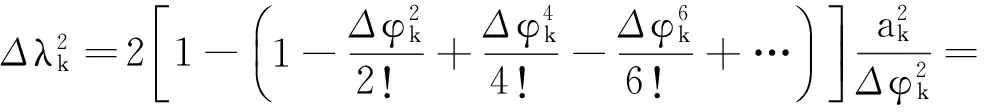
(22)

进而计算AGV在导航坐标系中的位置变化：

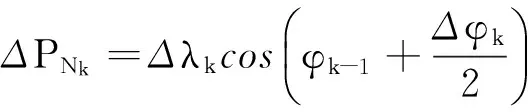
(23)

由于行驶地面不可能绝对水平，笔者考虑AGV轻微的横滚和俯仰，将位置变化量投影到水平面，则可以进一步表示为：

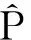
(24)

AGV在k+1时刻的位置和偏航角可以表示为：

(25)

φk+1=φk+Δφk

(26)

速度则可以通过求微分得到：

(27)

3 卡尔曼滤波器

本文将惯性导航和测距法相结合。采用KF对编码器和惯性传感器的数据进行融合。线性随机差分方程为：

xk=Axk-1+Buk-1+wk-1

(28)

zk=Hxk+vk

(29)

随机变量wk和vk分别表示过程噪声和测量噪声。相应的时间更新方程和测量更新方程[18]为：

(30)

(31)

(32)

(33)

(34)

由于先验估计和后验估计是线性关系，并假设速度和姿态的相关系数为0，则A是单位矩阵。

输入变量(加速度、角速度)和状态变量只与测量的时间间隔和转换矩阵有关，故有：

(35)

B=Δt×I6×6

(36)

测量量和状态量是线性关系，但测量量彼此之间不相关，则有：

H=I6×6

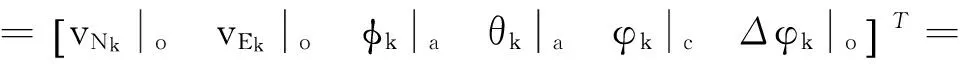
Hxk

(37)

式中：下标o—由里程计算法计算所得；下标a—由公式(2，3)计算所得；下标c—由磁强计计算所得。

其中，过程噪声协方差来自惯性传感器的测量过程，假设惯性传感器彼此之间不相关，则有：

(38)

式中：Qf—加速度的噪声协方差。

姿态的协方差是陀螺仪输出的一次积分：

(39)

式中：Nangle—陀螺仪的白噪声；Qgyro—陀螺仪的噪声协方差。

过程噪声协方差为：

(40)

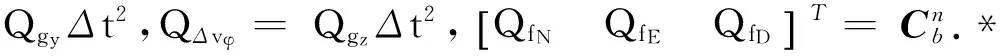
测量的噪声协方差来自编码器和磁强计，同时假设加速度计和磁强计以及编码器不相关，则有：

(41)

式中：RvN，RvE，RΔφ—由编码器估计的速度、偏航角变化量的误差协方差；Rφ，Rθ—来自加速度计的误差协方差；Rφ—来自磁强计的误差协方差。

算法流程图如图3所示。

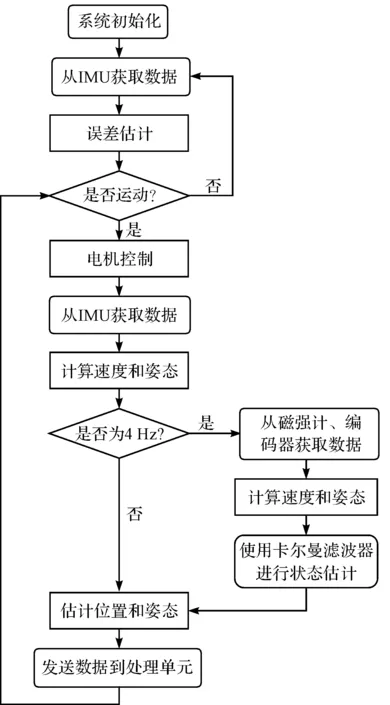
图3 算法流程图

4 实验

为了验证算法的有效性，本研究搭建了两轮驱动实验平台。其中，编码器安装在两驱动轮上，IMU传感器选用的是Advanced navigation公司的Orientus产品。

4.1 误差补偿实验

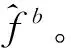
结果如图4所示。

补偿后的角速度几乎为0，并且状态稳定，达到了非常好的补偿效果。

图4 对加速度计的误差补偿

图5 对陀螺仪的误差补偿

4.2 位置估计实验

实验的预设路径为直径9 700 mm的圆形，控制AGV跟踪该路径运行50次，根据采集的数据绘制图如图(6～7)所示。

图6 里程计

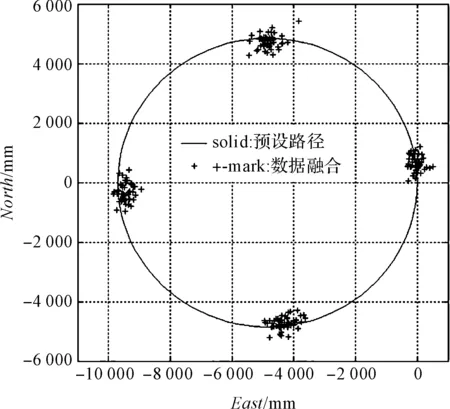
图7 卡尔曼滤波

由图(6～7)可见，测距法估计出比真实圆形更小的位置，而卡尔曼滤波的结果在真实数据的上下波动，虽然方差较大，但具有更高的准确性。具体地，两种方式在4个位置的均值和标准差，位置估计实验数据如表1所示。

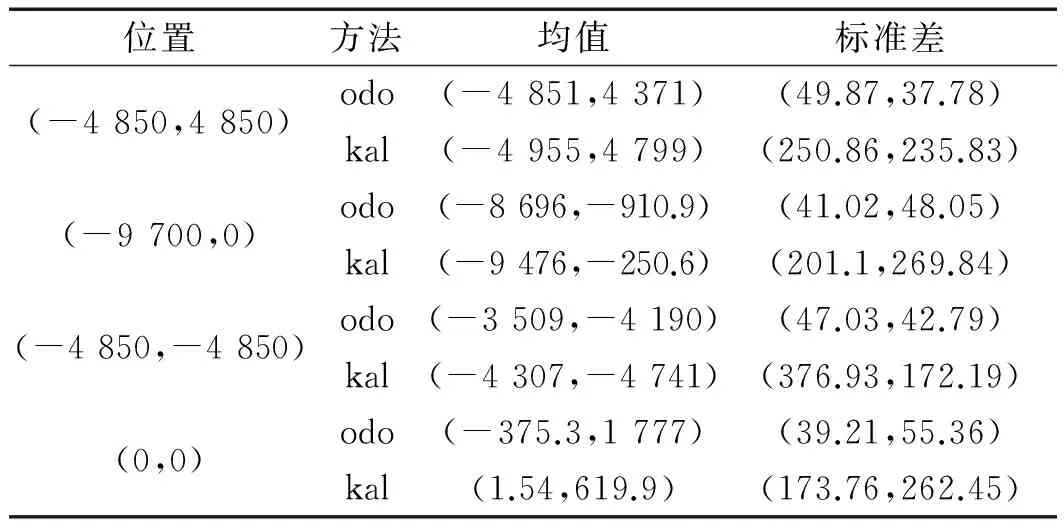
表1 位置估计实验数据

Odo—单独使用里程计算法；kal—本文提出的算法

由此可见，与仅使用里程计算法相比，本文提出的算法具有更高的准确性。

5 结束语

针对AGV的室内定位问题，本文提出了一种相对位置估计算法来实现航迹推算，其结合了惯性导航系统与里程计算法。为了补偿惯性导航与里程计算法中的累积误差，本研究设计了卡尔曼滤波器来对传感器的数据进行融合。最后基于两轮AGV实验平台，本研究对误差补偿算法与位置估计算法进行了验证。

实验的结果表明：该算法有效地提升了位姿估计的精度与稳定性。为进一步借助外部信号来提升AGV的室内组合定位精度提供更好的相对定位基础，同时将有助于提升AGV定位系统在外部信号干扰与缺失时的稳定性。

[1] 倪维晨.自动导引车控制系统的研究与应用[D].天津：天津理工大学机械工程学院，2012.

[2] 刘佳耀，袁佳艳，陶卫军，等.一种配备智能机械臂的AGV设计与实现[J].兵工自动化，2016，35(10)：38-31.

[3] RONZONI D, OLMI R, SECCHI C, et al. AGV global localization using indistinguishable artificial landmarks[C]. 2011 IEEE International Conference on Robotics and Automation, Shanghai: IEEE，2011.

[4] YOON S W, PARK S B, KIM J S. Kalman filter sensor fusion for Mecanum wheeled automated guided vehicle localization[J].JournalofSensors，2015(8)：1-7.

[5] NAGASAKA Y, TAMAKI K, NISHIWAKI K, et al. A global positioning system guided automated rice transplanter[J].IFACProceedingsVolumes，2013，46(18):41-46.

[6] YAYAN U, YUCEL H, YAZICI A. A low cost ultrasonic based positioning system for the indoor navigation of mobile robots[J].JournalofIntelligent&RoboticSystems，2015，78(3-4):541.

[7] UREA J, GUALDA D, HERNNDEZ, et al. Ultrasonic local positioning system for mobile robot navigation: from low to high level processing[C].2015 IEEE International Conference on Industrial Technology, Seville: IEEE，2015.

[8] ROEHRIG C, HELLER A, HESS D, et al. Global localization and position tracking of automatic guided vehicles using passive RFID technology[C]. Proceeding of 41st International Symposium on Robotics, Munchen: IEEE,2014.

[9] PIERLOT V, DROOGENBROECK M V. A new three object triangulation algorithm for mobile robot positioning[J].IEEETransactionsonRobotics，2014，30(3):566-577.

[10] SILVA O D, MANN G K I, GOSINE R G. An ultrasonic and vision-based relative positioning sensor for multirobot localization[J].IEEESensorsJournal，2015，15(3):1716-1726.

[11] OMARI S, BLOESCH M, GOHL P, et al. Dense visual-inertial navigation system for mobile robots[C]. 2015 IEEE International Conference on Robotics and Automation(ICRA), Washington: IEEE，2015.

[12] MARTNEZ B H, HERRERO P D. Autonomous navigation of an automated guided vehicle in industrial environments[J].RoboticsandComputer-IntegratedManufacturing，2010，26(4):296-311.

[13] AOKI H, ANN R S, TANAKA A, et al. Odometer correction method using disturbed environmental magnetic field[C].2014 IEEE 3rd Global Conference on Consumer Electronics, Tokyo: IEEE，2014.

[14] LU M F, LIU B C, WU J P, et al. The indoor automatic guided vehicle with an IR positioning and low-cost inertial navigation system[J].AppliedMechanicsandMaterials,2013(300-301):494-499.

[15] HELLMERS H, NORRDINE A, BLANKENBACH J, et al. An IMU/magnetometer-based indoor positioning system using kalman filtering[C].2013 International Conference on Indoor Positioning and Indoor Navigation, Guimaraes: IEEE，2013.

[16] 张永泽，艾长胜，张 尉.惯导与视觉相结合的AGV小车控制系统设计[J].山东工业技术，2015(20):236-236.

[17] NOURELDIN A, KARAMAT T B, GEORGY J. Fundamentals of inertial navigation, satellite-based positioning and their integration[M]. Berlin: Springer Berlin Heidelberg，2013.

[18] BISHOP G, WELCH G. An introduction to the kalman filter[J].UniversityofNorthCarolinaatChapelHill，2013，8(7)：127-132.