基于双S形速度曲线的混联码垛机器人轨迹规划

张志松

(比特数控技术应用有限公司，河北 廊坊 065000)

0 引 言

伴随着“中国制造2025”概念的提出，国内迎来了工业机器人的发展热潮[1-2]。搬运码垛机器人以其高柔性工作能力、占地面积小、高效完成箱包装物品搬运的优势，在物流仓储领域得到广泛应用[3]。由于机器人对搬运与码垛的工作效率要求比较高，在工作过程中频繁地快速启动、停止，对机械结构的冲击和磨损很严重。因此，为了实现搬运机器人在码垛过程中快速、平稳的运动控制，这就需要研究出关于时间和空间比较复杂的位置、速度、加速度函数，以满足搬运码垛机器人的控制要求。

机器人轨迹规划描述了操作臂在笛卡尔空间和关节空间的运动曲线，其遵循的一个原则就是运动过程中避免速度及加速度突变，保持轨迹平稳平滑[4]。目前机器人关节空间轨迹规划方法大都用的是高阶多项式插值[5-7]、样条插值等方法[8-10]。

本文将通过对现有的轨迹曲线进行分析，设计出性能优越、符合要求的轨迹曲线，从而实现搬运码垛机器人高精度的实时运动控制。

1 码垛机器人运动学分析

根据码垛机器人实际工作需求，笔者在遵循机器人构型选择的基础上，设计了串—并混联式圆柱坐标构型码垛机器人，其构型如图1所示。

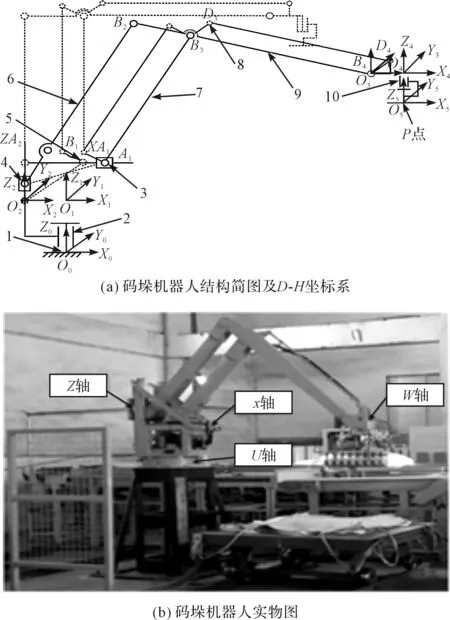
图1 混联式码垛机器人1—底座；2—腰座；3—水平直线单元；4—竖直直线单元；5—大臂连杆；6—后大臂；7—前大臂；8—转动铰链；9—小臂；10—腕部

该码垛机器人主要由腰部、后大臂、前大臂和腕部4部分组成，其中腰部关节实现底座1与腰座2的相对转动，水平直线单元3与竖直直线单元4分别驱动后大臂6，前大臂7实现机器人腕部的水平和竖直方向运动，腕部关节实现腕部10与末端执行器的相对转动，同时利用A1-B1-B2-B3以及B3-D3-D4-B4两组辅助平行四边形机构使机器人末端始终保持水平，可以实现对末端工具竖直位移和水平位移的解耦控制。这种构型一方面保留了圆柱坐标型的运动直观、结构较为简单、动作范围大且在动作范围内无奇异点、控制计算量小、运行速度快等诸多优点；另一方面利用了混联机构所综合的串联机构较大的工作空间和并联机构较大的结构刚度等优点，在提高机器人的作业能力、节约制造成本等方面具有明显的优势。

1.1 码垛机器人正运动学分析

1.1.1 平行四边形机构运动学分析

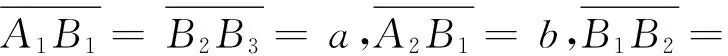
(1)

当两直线单元分别由零位运动到图1中某一位姿时(实线表示)，铰接点A1，A2，B1，B2，B3在坐标系X2O2Z2中的齐次坐标可分别表示为：

(2)

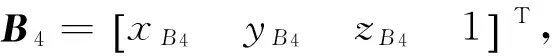
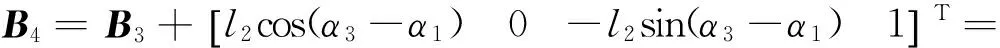
(3)

从而可得臂部平行四边形机构的运动学关系为：

(4)

当连杆A1B1，A2B1，B1B2，B3B4的长度b,a,l1,l2满足一定几何约束时，式(4)可通过如下过程进行求解。在图1中，根据几何关系，进一步可得：

(5)

从而可推出：

(6)

当l1/b=l2/a=j(j为常数)时，则式(6)可表示为：

(7)

将式(7)代入式(4)，可得：

(8)

式(8)即为码垛机器人平行四边形机构的运动学关系式。由于zB4与zA2、xB4与xA1均为线性关系，小臂末端铰接点B4的竖直位移和水平位移在垂直面内实现了运动解耦。

1.1.2 码垛机器人正运动学方程

笔者建立码垛机器人的D-H坐标系，对应的D-H参数如表1所示。

表1 码垛机器人D-H参数

则相邻坐标系的变换矩阵分别为：

本研究将以上5个矩阵相乘，得到码垛机器人正运动学方程：

(9)

由式(9)可看出，码垛机器人末端工具的位置是由臂部平行四边形机构关节变量xA1和zA2及底座的旋转关节变量θ0决定的，姿态由底座和腕部的旋转关节变量θ0和θ4决定，因此该构型的机器人相对通用关节式机器人更易于控制。

1.2 码垛机器人逆运动学分析

为了对机器人进行运动控制和轨迹规划，需求解机器人的逆运动学方程。当机器人的连杆长度满足式(8)时，结合式(9)，有如下关系：

(10)

若机器人末端坐标系X5O5Z5相对于基坐标系X0O0Z0的转角(绕Z0轴)为β，则有：

(11)

根据式(9)可知：θ0+θ4=β，则

θ4=β-θ0

(12)

式(11)和式(12)即为该混联机器人的逆运动学方程。

2 码垛机器人轨迹规划

由于码垛机器人在高速运行过程中频繁地快速启动与停止，其加减速控制极为重要，这就要求加速度曲线首尾两端的光滑度要好，避免加速度突变。因此，只有采用合适的运动轨迹曲线才能同时保证运动速度的高效和减小机械本体所受到冲击。在通过逆运动学计算获取码垛机器人各关节位置相对时间的序列值之后，本研究采用双S形速度曲线进行码垛机器人轨迹曲线的规划。

轨迹的速度曲线两端是由抛物线连接的，形状类似英文字母“S”，所以称之为双S形速度曲线。又由于该轨迹由7段不同的常量Jerk曲线组成，笔者将其称之为7段轨迹。

典型轨迹如图2所示。

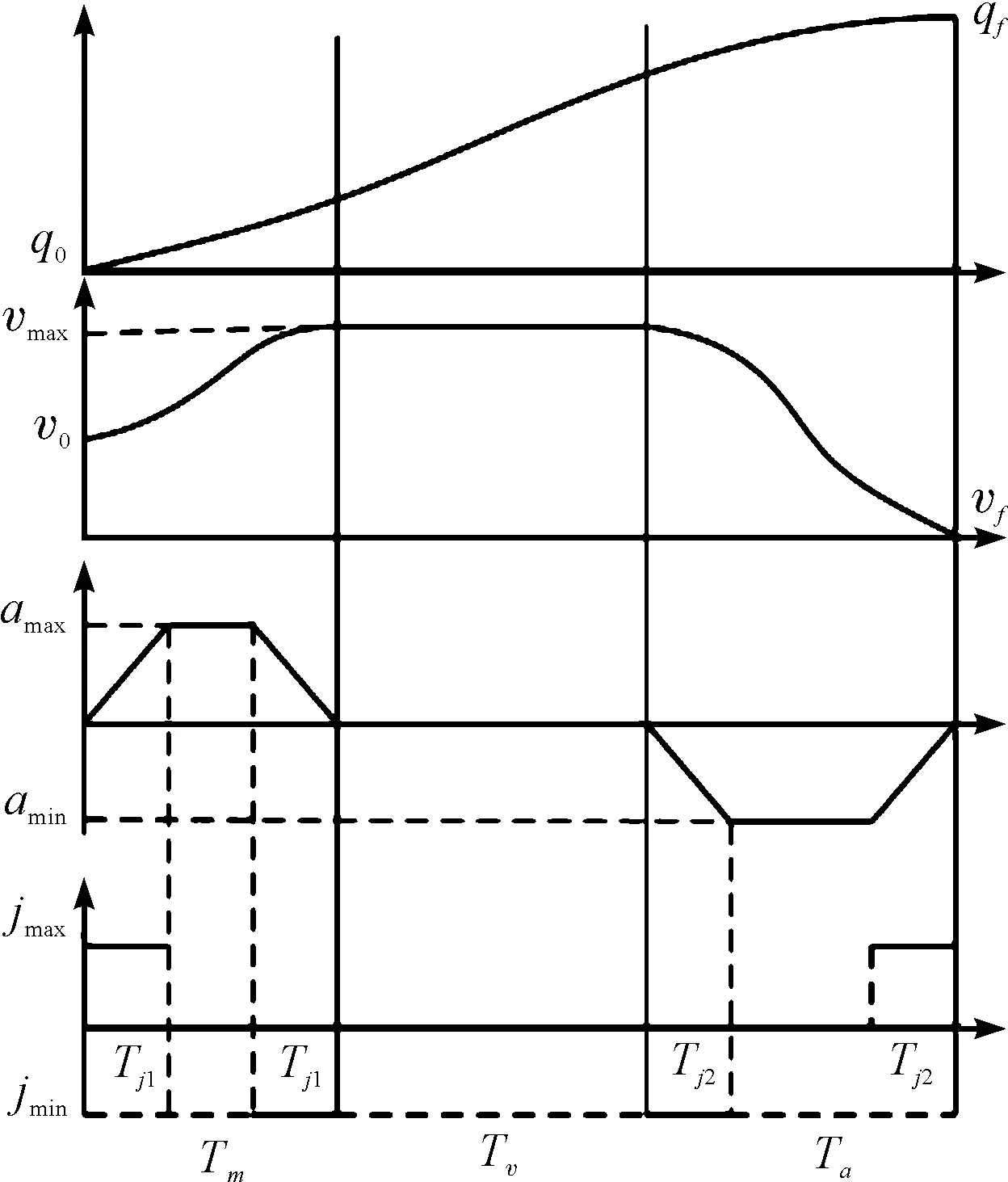
图2 双S形速度轨迹的位置、速度、加速度和Jerk曲线

本研究以码垛机器人某一个关节角位置信息为研究对象，以函数qi(t)表示轨迹曲线，即：

q=qi(t),t∈[t0,tf]

(13)

为了获得一条确定的光滑运动曲线，假设qf>q0，且t0=0，设轨迹曲线的边界条件为：

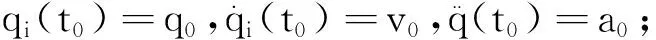
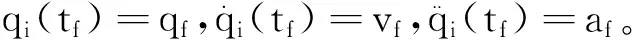
图2中的Tf1，Tj2为Jerk不为零(变加速)的持续时间，Tv为匀速运动时间。速度、加速度、Jerk满足vmin=-vmax、amin=-amax、jmin=-jmax，即运动约束条件关于原点对称。将双S形速度轨迹分成如下3个运动阶段。

第一阶段为加速阶段：t∈[0,Ta]，加速度从零线性增加到最大值，然后线性减小到零。

在t∈[0,Tj1]阶段：

(14)

在t∈[Tj1,Ta-Tj1]阶段：

(15)

在t∈[Tj1,Ta-Tj1]阶段：

(16)

第二阶段为最大速度运行阶段：t∈[Ta,Ta+Tv]，该阶段轨迹的速度为常量。

在t∈[Ta,Ta+Tv]阶段：

(17)

第三阶段为减速阶段：t∈[Ta+Tv,T]，此阶段的加速度的变化规律和第一阶段中加速度的变化规律相同，方向相反。

在t∈[T-Td,T-Td+Tj2]阶段：

(18)

在t∈[T-Td+Tj2,Ta-Tj2]阶段：

(19)

在t∈[T-Tj2,T]阶段：

(20)

3 仿真与分析

为了验证双S形速度曲线对码垛机器人关节空间进行轨迹规划的有效性，本研究给定轨迹的边界条件为：q0=0，q1=10和v0=1，v1=0，约束条件为：vmax=10，amax=10和jmax=30。

对应的关节运动仿真曲线如图3所示。

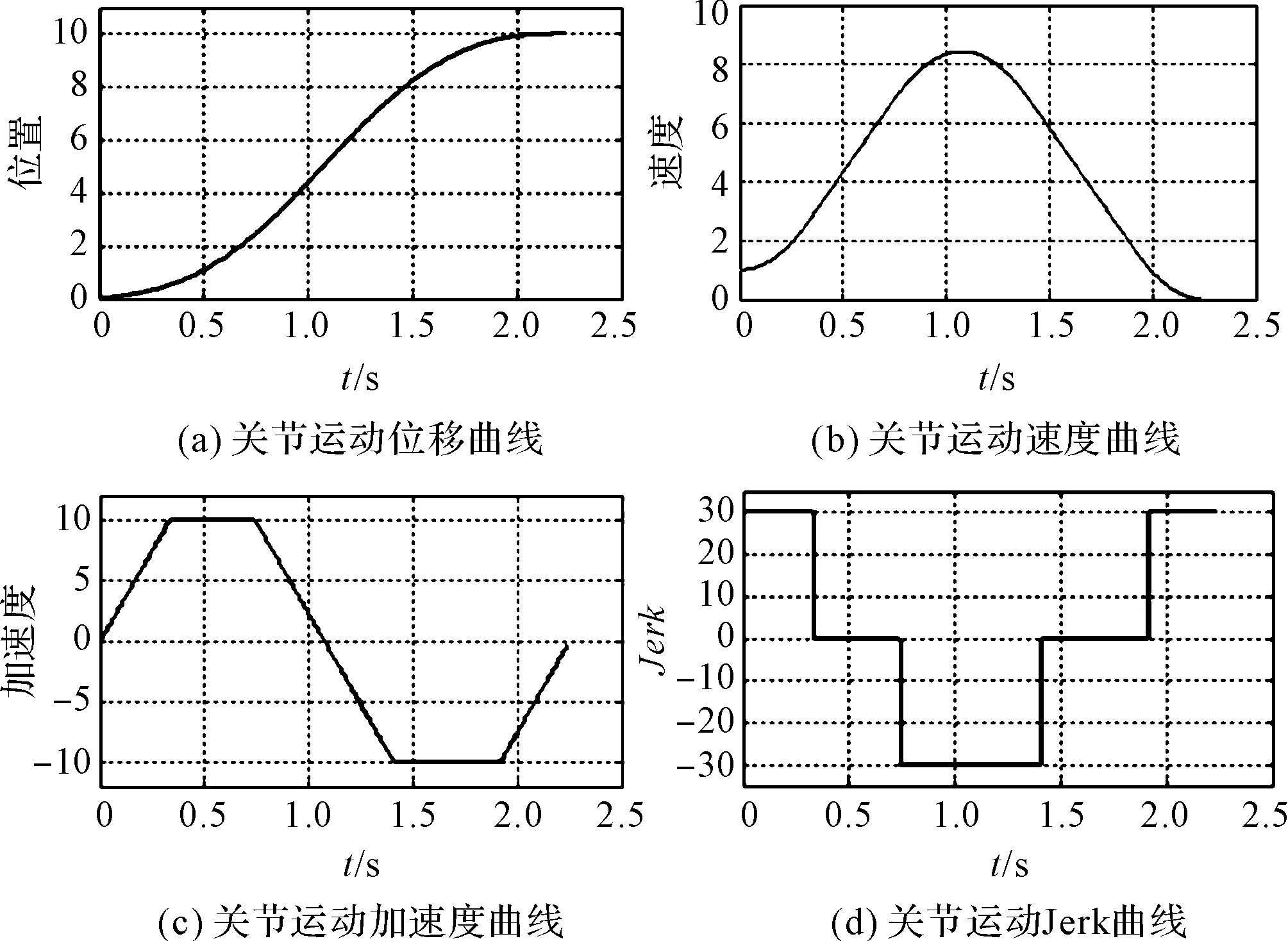
图3 双S形速度轨迹的仿真曲线

从图3(a～d)的仿真曲线可以看出：给定码垛机器人起始点和终止点的关节角度值，机器人关节轴在运行中满足位移、速度、加速度、Jerk连续性的约束条件，并且轨迹曲线首尾两端的平滑性很好，避免了机器人在高速运行过程中因频繁快速地启动与停止对机械系统产生的冲击、磨损问题，实现了机器人系统高速平稳的运动到指定位置的控制要求。

4 结束语

结合码垛机器人实际工作需求，本文设计了串—并混联式圆柱坐标构型的码垛机器人，该构型机器人在提高机器人的码垛能力等方面具有明显的优势。

本研究推导了混联式圆柱坐标型码垛机器人正、逆运动学，引入双S型速度曲线完成了该机器人关节空间的轨迹规划。Matlab仿真表明：该轨迹规划方法保证了机器人关节位移、速度、加速度、Jerk曲线的连续光滑，能够减小其在加减速运行过程中的冲击，提高整个机器人系统的稳定性和可靠性。

[1] 工信部装备工业司.《中国制造2025》推动机器人发展[J].机器人技术与应用，2015(3):31-33.

[2] 刘 勇，张 亮.发展智能制造，促进兵器装备集团制造工业转型升级——兵器装备集团智能制造技术与高端装备产业发展思考[J].兵工自动化，2017，36(1)：1-6.

[3] 孙 浩.码垛机器人的设计与研究[D].济南：山东理工大学机械工程学院，2013.

[4] 蔡自兴.机器人学[M].北京:清华大学出版社，2000.

[5] 张道德，徐 波.机器人多段插值轨迹规划研究与分析[J].湖北工业大学学报，2016，31(5):1-3.

[6] 涂 孔，张 华.变插值周期五次多项式机器人关节空间规划[J].浙江理工大学学报：自然科学版，2017，37(3)：33-37.

[7] 郭瑞峰，彭光宇，杨 柳，等.基于MDH模型的新型混联码垛机器人运动学分析与仿真[J].机械传动，2017(2):122-127.

[8] 李亮玉，龙 洋，王天琪，等.基于有理B样条曲线的焊接机器人操作空间轨迹规划[J].天津工业大学学报，2015，34(6):80-83.

[9] 赵 皓，刘满禄，张 华.基于三次非均匀B样条的6DOF机械臂轨迹规划[J].机器人技术与应用，2016(6):43-48

[10] 赵 春，甘 戈，蒋哲文.关节一体化机器人运动控制与B样条曲线[J].机械设计与制造，2017(1):258-261.