基于子模型技术的转向架构架疲劳寿命预测*

杨 宏，王 红，商跃进

(兰州交通大学 机电工程学院，甘肃 兰州 730070)

0 引 言

转向架在铁道车辆运行过程中主要起到接收轨道激励的作用，其构架起到支撑、连接、传递等作用，是转向架的重要部件之一。由于轨道车辆运行过程中长期承受复杂的交变载荷，极易诱发焊接构架的焊缝产生裂纹，造成安全事故[1]。焊接疲劳破坏通常发生在焊趾处，并沿着焊趾在厚度方向上扩展[2]。因此，为保证铁道车辆的安全运行，对转向架构架的疲劳寿命进行评估和预测具有一定的现实意义。

目前主要参考基于名义应力法的ⅡW和BS标准以及ASME标准计算焊接接头的疲劳寿命。采用ⅡW和BS标准计算焊接接头疲劳寿命时，需在标准中找出与之对应的焊接接头的S-N曲线数据。考虑实际应用情况，如果焊接接头的几何形状和受力比较复杂时，在标准中很难找出与之完全对应的接头类型，如果近似选择，则会造成较大误差。而于2007年被纳入美国ASME标准的等效结构应立法则有效的避免了这种问题，它不受接头类型的限制，并且具有网格不敏感性。

国内很多学者都对车辆零部件的疲劳强度进行过研究，沈彩瑜、米彩盈[3]基于名义应力法对车体的疲劳寿命进行了估算。王斌杰、王红等[4-5]使用热点应力法对转向架构架进行了疲劳强度评估。赵峰翔、张开林等[6]在确定好焊接构架评估所需的S-N曲线的基础上，采用名义应力法和局部缺口应力法估算了关键焊缝的疲劳寿命，并对两种方法进行对比。刘洪涛、谭富星等[7]采用BS方法对焊接构架进行了疲劳强度分析。基于CRH380B动车组转向架构架通过静强度计算后的局部应力分析得到平均应力和应力幅较大位置，在建立子模型的基础上采用由董平沙教授提出的基于等效结构应力法的主S-N曲线疲劳寿命预测方法[8]对其关键焊缝进行疲劳寿命计算。

1 构架整体模型分析

1.1 构架结构特点

采用的CRH380B转向架采用转臂轴箱定位方式，构架通过一系钢簧和转臂定位的方式和轮对链接在一起，一系钢簧决定其垂向刚度，转臂节点处的弹性衬套决定其横向和纵向刚度。构架是由两根中部下凹的鱼腹箱型侧梁和两根无缝钢管组成的H型结构，横梁上焊有纵向辅助梁。分析时考虑构架的结构和承载特点，对其进行简化。构架使用的材料是S33J2G，属于高强度耐候钢板，其拉伸强度为510 MPa、屈服强度为355 MPa、弹性模量为2.06×105MPa、密度为7.8×10-6kg/mm3、泊松比为0.29。

根据UIC566标准[9]，静强度评定时，正常运营工况下母材的安全系数取为1.5，许用应力236 MPa；焊缝区的安全系数为1.65，许用应力为215 MPa。

1.2 构架强度分析

1.2.1有限元模型的建立

建立有限元模型是进行有限元分析的基础工作。构架采用C3D10(10节点二次四面体单元)进行离散，离散单元数为237 384个，节点数为459 450个，有限元模型如图1所示。根据实际受力情况，确定约束和加载位置，如图2所示。在Abaqus中通过建立弹簧单元来模拟一系钢簧和转臂节点处的弹性衬套，根据实际刚度值赋予弹簧属性。

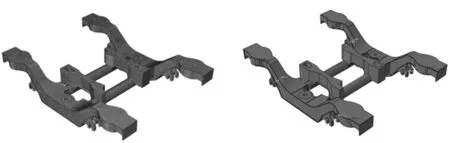
图1 构架的有限元模型 图2 构架的约束和加载位置

1.2.2载荷工况的确定

(1) 静强度载荷工况的确定

为验证构架静强度是否符合要求，并为后面局部应力分析做准备，根据UIC615-4标准[10]确定构架的加载工况，计算13种模拟运营工况下的静强度，构架载荷工况见表1。构架静强度试验载荷分为横向、纵向和斜对称载荷。

表1 运营载荷工况列表

(2) 疲劳载荷工况的确定

根据UIC615-4标准，确定动力转向架焊接构架的疲劳加载工况，构架疲劳试验载荷分为垂向和横向两种，并对其进行分步加载，加载情况如下：垂向载荷为Fz(同模拟运营工况中静态试验时的垂向力)，横向载荷为Fy(同模拟运营工况中静态试验时的横向力)。约束及加载位置同模拟运营工况。

1.3 计算结果分析

1.3.1静强度计算结果分析

通过计算得到13种模拟载荷工况下的静强度结果，其中最大等效应力为185.2 MPa，出现在空气弹簧安装孔处，没有超出许用应力235 MPa，满足强度要求。

根据疲劳评估点选取原则，即结合焊接构架的静强度分析结果和焊接形式来确定疲劳危险位置。笔者主要分析关键焊缝的疲劳寿命，所以，根据以上原则选取构架上三个焊缝连接处作为评估点进行局部应力分析，统计13种模拟工况下这三个位置处的应力值，确定最大、最小应力，求出平均应力及应力幅。其选取位置如图3所示，应力分析情况见表2。

表2 构架局部应力分析 /MPa

由表2可知，转臂定位座与侧梁连接处的平均应力和应力幅较大，所以，需要对此处的焊缝结构进行细化，分析其焊缝疲劳寿命是否符合要求。

1.3.2疲劳工况计算结果分析

通过计算得到疲劳工况的应力分布如图4所示，最大等效应力为146.1 MPa。

图3 构架局部应力分析位置 图4 疲劳工况的应力云图

2 子模型的建立

由于构架属于大型构件，对其关键部位运用子模型技术，节约计算时间的同时也能提高计算精度。通过对以上分析中得出的焊缝疲劳薄弱区建立子模型，将焊缝进行细化，计算其疲劳寿命。

2.1 子模型技术简介

子模型分析是指在完成全局模型分析之后，再把全局模型局部位置的网格进行细化用于后期计算，这样既节约了时间又使计算结果更加精确。子模型技术最重要的是切割边界的确定，从全局较粗网格模型上分割开的边界就是切割边界，而子模型的边界条件是切割边界的计算位移值[11]。

子模型基于圣维南原理，即应力分布只对载荷作用区域有影响，此区域会存在应力集中效应。所以，在进行子模型分析时，切割边界需要远离应力集中区域，这样才能得到更精确的分析结果[12]。

2.2 子模型的创建方法

选用基于节点的子模型技术在Abaqus中实现子模型的创建。通过以下步骤来实现子模型分析：

(1) 全局模型分析完成后保存应力分析结果。

(2) 完成子模型的切割，将切割边界处的节点定义为子模型切割边界。

(3) 对各个分析步中的驱动变量进行设置。

(4) 对子模型的边界条件、载荷、接触和约束进行设置。

(5) 完成子模型分析，验证切割边界条件[13]。

一般通过查看子模型边界附近的结果变量值及云图变化与全局模型是否一致来判断子模型建立的正确性，如果结果一致，则认为该子模型是有效的。

2.3 计算结果分析

通过上述方法创建构架转臂定位座处的子模型，子模型的应力分布如图5所示。和全局模型相应位置的应力分布相比较可知，子模型的应力分布与全局模型相应位置基本一致。再对切割边界进行校核，笔者仅选取子模型下盖板一侧的应力曲线与整体模型相应位置的应力曲线进行对比，如图6所示。

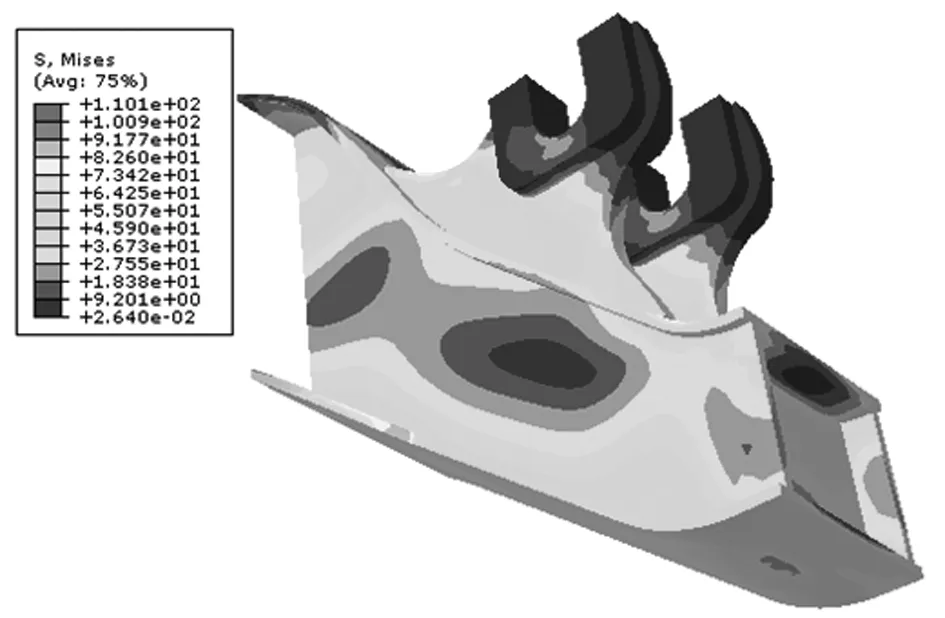
图5 子模型的应力计算结果

由图6可知，子模型和全局模型在切割边界处的等效应力值基本一致，由此证明切割边界的选取是合理的，可以用于后续焊缝寿命的计算。

图6 子模型和全局模型在切割边界处应力对比图

3 基于子模型的焊缝疲劳寿命预测

为了估算焊缝薄弱区的疲劳寿命，在以上转臂定位座处子模型计算结果的基础上，采用等效结构应力法计算其四条焊缝的疲劳寿命。

3.1 等效结构应力法原理

等效结构应力法主要有两个关键技术，即网格的不敏感性和一条主S-N曲线。其中网格的不敏感性是通过焊趾处任意板厚应力状态的平衡等效来实现的。等效结构应力法中焊趾部位的应力由两部分组成，即由外力引起结构应力和由焊接工艺引起峰值应力。首先通过整体坐标系向局部坐标系的转换得到节点力和力矩；根据节点力和力矩的平衡，推出结构应力；基于断裂力学理论，将结构应力转化为等效结构应力，其转化方程为式(1)。式中同时考虑了焊缝应力集中、板厚尺寸、载荷模式的影响。

(1)

(2)

式中：ΔSs为等效结构应力变化范围；Δσs为结构应力变化范围；t为结构板厚尺寸；I(r)为载荷弯曲比r(r=Δσb/Δσs)的无量纲函数；a为裂纹任意方向上的长度；Mkn为应力强度放大系数；fm(a/t)、fb(a/t)分别为膜正应力和弯曲正应力作用下的无量纲函数。

通过下式计算焊缝的疲劳寿命：

(3)

式中：C、h为ASME提供的主S-N曲线试验常数;N为疲劳寿命循环次数。

3.2 焊缝疲劳寿命计算

通过Fe-safe软件中的Verity模块计算焊缝的疲劳寿命。将Abaqus中计算生成的odb文件导入Fe-safe的Verity模块中进行计算，首先需要设置焊缝属性，四条焊缝的焊线节点及焊线参考单元分别如图7和8所示。

在对焊接构架进行疲劳寿命分析之前，需要定义材料属性，对构架焊缝疲劳寿命评估选用的材料为Steel-Weld(50%)。并对疲劳载荷谱进行设定，按照UIC615-4疲劳加载标准，垂向载荷由0.7Fz到1.3Fz变化，平均应力为Fz，横向力由0到±Fy变化。动态疲劳采用三级加载方式，第一级加载的循环次数为6×106次，第二级加载的循环次数为2×106次，第三级加载的循环次数为2×106次，共1000万次，载荷放大系数在三个阶段分别为1.0、1.2和1.4。

图7 焊线位置图 图8 焊线参考单元

3.3 计算结果分析

通过式(1)、(2)计算得到四条焊线节点的等效结构应力，其结构应力和等效结构应力的对比如图9～12所示。

图9 焊缝1结构应力及等效结构应力

图10 焊缝2结构应力及等效结构应力

在Fe-safe中计算得到焊缝处的疲劳寿命后在Abaqus中查看寿命云图，如图13所示，图中显示的是对数疲劳寿命值。由计算结果可得四条焊缝的寿命，如表4，最小疲劳寿命为1.172×107次，符合UIC615-4标准规定的1×107次，所以构架疲劳强度满足设计要求。

图11 焊缝3结构应力及等效结构应力

图12 焊缝4结构应力及等效结构应力

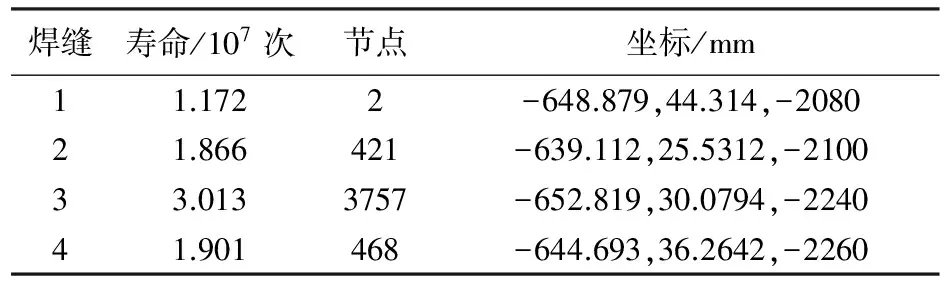
焊缝寿命/107次节点坐标/mm11．1722-648．879，44．314，-208021．866421-639．112，25．5312，-210033．0133757-652．819，30．0794，-224041．901468-644．693，36．2642，-2260

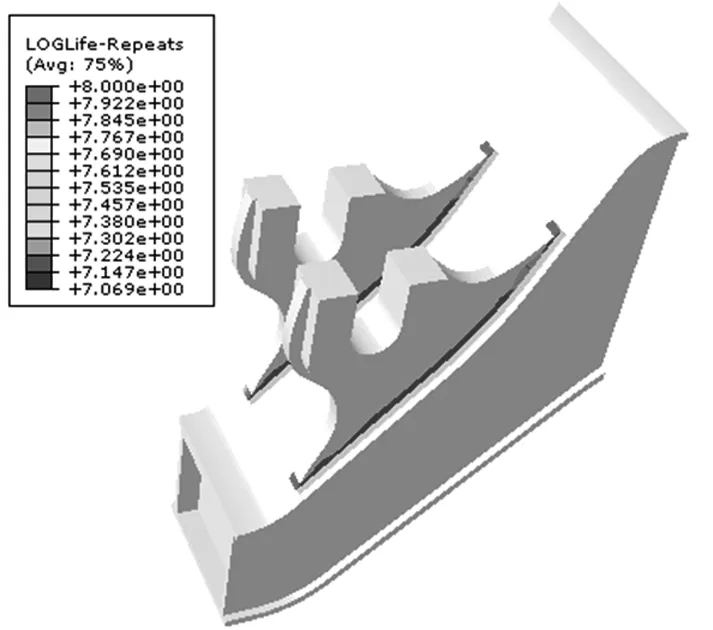
图13 焊缝疲劳寿命分布图

4 结 论

通过对CRH380B型动车组强度及焊缝疲劳寿命的分析，得出结论：

(1) 通过计算13种模拟运营工况的静强度，对构架三个部位的局部应力进行分析，得到转臂定位座处的平均应力和应力幅较大。

(2) 计算构架整体在疲劳工况下的应力，对其转臂定位座建立子模型，并对子模型的切割边界进行了验证，结果表明切割边界选取正确。

(3) 在子模型的基础上，采用美国ASME标准中

的等效结构应力法进行了焊缝疲劳寿命计算。计算结果表明，最小寿命出现在转臂定位座上的第一条焊缝处，其疲劳寿命为1.172×107次，符合UIC615-4标准的设计要求。

(4) 正确应用子模型技术能够保证计算的准确性，运用子模型和全局模型相结合的方式计算局部位置处的疲劳寿命，能够节约转向架的设计时间和成本，同时也为下一步的优化设计奠定了基础，这也是复杂结构疲劳分析可以借鉴的一种有效方法。

[1] 沈彩瑜.铁道车辆转向架构架疲劳强度研究[D].成都:西南交通大学,2014.

[2] 李向伟,兆文忠.基于Verity方法的焊缝疲劳评估原理及验证[J].焊接学报,2010(7):9-12+113.

[3] 沈彩瑜,米彩盈.重载电力机车车体强度和刚度研究[J].计算机仿真,2014,31(2):230-234.

[4] 王斌杰.高速列车结构热点应力疲劳评定方法及应用研究[D].北京:北京交通大学,2008.

[5] 王等红,刘万选,商跃进.基于热点应力的国产化Y25型转向架焊接构架疲劳强度分析[J].中国铁道科学,2013,34(4):66-70.

[6] 赵峰强,张开林,刘等斌.出口缅甸3B0机车焊接构架疲劳寿命预测[J].机车电传动,2017(1):51-54+60.

[7] 刘洪涛,谭富星,于 寅,等.基于BS方法的拖车转向架焊接构架的疲劳评估[J].大连交通大学学报,2014,35(6):23-26.

[8] Dong P,Hong J K,Osaged,et al.Master S-N Curve method for fatigue evaluation of welded components[R].New York: Welding Research Council,2002: 1250.

[9] UIC566-1990,loadings of coach bodies and their components[S].1990.

[10] UIC615-4-2003,Motive power units-bogie and running gear-bogie frame structure strength tests[S].2003.

[11] 周 宇.基于子模型的铁路车辆结构强度精细计算[J].铁道机车车辆,2009(1):16-18.

[12] 马思群,张国磊,陈 轩,等.子模型技术在转向架构架疲劳寿命预测中的应用[J].农业装备与车辆工程,2016(3):1-4+17.

[13] 石亦平,周玉蓉.ABAQUS有限元分析实例详解[M].北京:机械工业出版社,2010.