非线性方程组求解器及平面连杆机构仿真程序研究*
柳冬玉,潘亚嘉
(西南交通大学 机械工程学院,四川 成都 610031)
0 引 言
传统的机构设计有几何法和解析法。在对某一特定机构进行参数分析时,可使用CAD软件建模,进而进行机构分析。为分析机构而进行三维建模耗工耗时,部分CAD软件虽然具备骨架功能,但操作仍较繁琐。对于机构的运动学问题,手工计算或者编程求解又面临求解非线性方程组的问题,研究简明易用的平面连杆机构仿真程序十分必要。
目前平面机构仿真程序有以下几类:
(1) 专门针对特定机构的程序,首先让用户从几种固定的机构类型中做出选择,再输入尺寸进行仿真,或者输入设计目标得到机构尺寸。此类程序算法固定,不能够处理内置机构以外的类型。
(2) 以杆组理论为核心的通用平面机构仿真程序,用户必须以杆组为基本单元进行输入[1-5]。
(3) 不依赖杆组,以单个杆件为基本元素的通用平面机构仿真程序。用户需输入杆件及其约束信息[6-7]。
基于杆组理论的机构仿真程序要求用户熟悉杆组分解,并且不能够求解程序中没有的杆组,具有先天缺陷。笔者在上述第3类程序的基础上,引入符号计算思想所进行的研究。
1 基于约束的运动学模型建立
1.1 机构的约束方程组的一般形式
设机构由一个约束方程组描述[8]为:
(1)

由式(1)可以解出机构在任意时间下的q,从而得出机构的位置。由于式(1)通常为高度非线性,所以大多使用数值方法求解。
由于解出的q非解析解,所以不能直接对q微分得到机构各构件的速度及加速度。
(2)
(3)
考虑由转动副和移动副构成的平面连杆机构,其基本约束形式为重合约束和共线约束。重合约束的方程形式为:
(4)
式中:xi,yi,φi为构件i的笛卡尔广义坐标;xj,yj,φj为构件j的笛卡尔广义坐标;xi′P,yi′P,xj′P,yj′P为两构件重合点P分别在构件i,j的固定坐标系上的坐标。若取其中一个构件的广义坐标为常数,则可得到机架点铰接活动构件的约束方程。
共线约束的方程形式为:

xi′Q)]×(xi-xj+xi′Pcosφi-xj′Pcosφj-
yi′Psinφi+yj′Psinφj)-[cosφi(xi′P-
xi′Q)-sinφi(yi′P-yi′Q)]×(yi-yj+
yi′Pcosφi-yj′Pcosφj+xi′Psinφi-
xj′Psinφj)≡0
Φ2t(i,j)=[cos(φi-φj)(yi′P-yi′Q)+
sin(φi-φj)(xi′P-xi′Q)](xj′P-xj′Q)-
[cos(φi-φj)(xi′P-xi′Q)-sin(φi-
(5)
式中:xi,yi,φi,xj,yj,φj含义同式(4);两构件间存在一条公共的线段PQ,点P和点Q在构件i,j的固定坐标系上的坐标分别为xi′P,yi′P,xj′P,yj′P和xi′Q,yi′Q,xj′Q,yj′Q。若取其中一个构件的广义坐标为常数,则可得到机架与活动构件共线的方程。
1.2 拖动约束方程
很多CAD软件都具有鼠标拖动零件查看机构运动的功能,拖动功能能够非常直观地反映机构的运动情况,允许用户拖动任一构件查看仿真效果。下面推导拖动约束方程。如图1所示,构件i在点MStart处被鼠标点击拖动至MDrag,构件受到其余约束方程的限制进行运动,广义坐标发生变化,但运动规律未知。
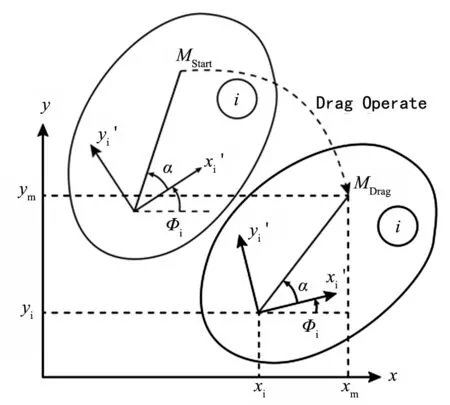
图1 构件i拖动前后示意
发生拖动前后,点M与构件的相对位置不发生变化,点M在坐标系xi′-yi′上的坐标为:
SM′=[xm′ym′]T
(6)
矢量SM与坐标轴xi′的夹角为:
(7)
点MDrag存在关系:
l=(xm-xi)sin(φi+α)
=(ym-yi)cos(φi+α)
(8)
式中:l为点M至坐标系xi′-yi′距离。
整理,得到拖动约束方程为:
(9)
已知一个机构系统的所有尺寸及其初始状态,列出所有转动副与移动副的约束方程,与驱动约束方程联立可得式(1),依次求解式(1)~(3)则可得到机构系统任意时刻的位移、速度及加速度。若与拖动约束方程联立求解,则可得到机构系统在受约束限制时拖动某一构件后的位置。
2 利用表达式树构建非线性约束方程组求解器
由于运动学方程是高度非线性的,其求解方式至关重要。基于牛顿—拉夫森迭代法的运动学约束方程求解在程序编制上通常使用固定矩阵法,其步骤如下:
(1) 事先展开所有运动副及驱动约束的位移、速度、加速度方程,推导特定约束对于两个构件的位移、速度、加速度方程右项。
(2) 在计算时代入构件的广义坐标,组合成位移、速度、加速度整体的数值矩阵,求解线性方程组后再根据迭代终止条件回代到位移、速度、加速度右项中继续迭代。
固定矩阵法整个求解过程不涉及符号推导,运算速度快,但是因为每种方程的计算表达式已经推导并且固化在程序中,所以无法为原动件设置自定义函数的运动规律,也无法求解运动学方程以外的方程。文献[8]讨论的即是此类求解器。
鉴于固定矩阵法的缺陷,引入符号计算思想及编译原理编制了通用非线性方程组求解器核心,在求解器核心的基础上添加自动列式功能及接口构成非线性约束方程组求解器。求解器可识别中序遍历表达式的非线性方程组字符串,并求出结果。文中的方法与固定矩阵法的求解流程图对比如图2所示。
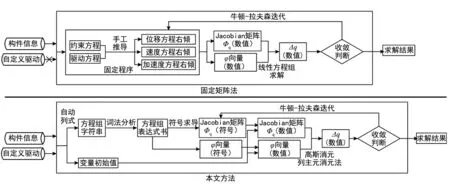
图2 固定矩阵法与文中方法求解流程对比
求解器功能由四个类实现:求解器类(TSolver)、方程组类(TEquations)、表达式树类(TExpressionTree)、变量表类(TVariableTable)。
变量表类用于保存变量名及其初始值;表达式树类用于将方程字符串解析为表达式树;方程组类用于存储各个方程的表达式树并对其求解,可独立求解非线性方程组;求解器类用于读取程序构件数据建立约束方程,对外提供方程组类中的求解结果的接口。
在方程组类内部,方程字符串由词法分析器解析为表达式树,表达式树进行符号求导得到由表达式树组成的雅可比(Jacobian)符号矩阵。雅可比符号矩阵及方程组均代入初值得到线性方程组,利用高斯消元中的列主元消元法得到Δq,同时判断出雅可比矩阵的奇异性。图3为基于表达式树的非线性方程组求解过程图。

图3 基于表达式树的非线性方程组求解过程
根据Δq进行收敛判断,若Δq大于设定值则继续迭代。若Δq小于设定精度则终止迭代并输出求解结果。
3 程序结构组成及设计
3.1 程序结构
程序以面向对象模式开发,其结构分为界面层、工具层、构件层和公共层,如图4所示。
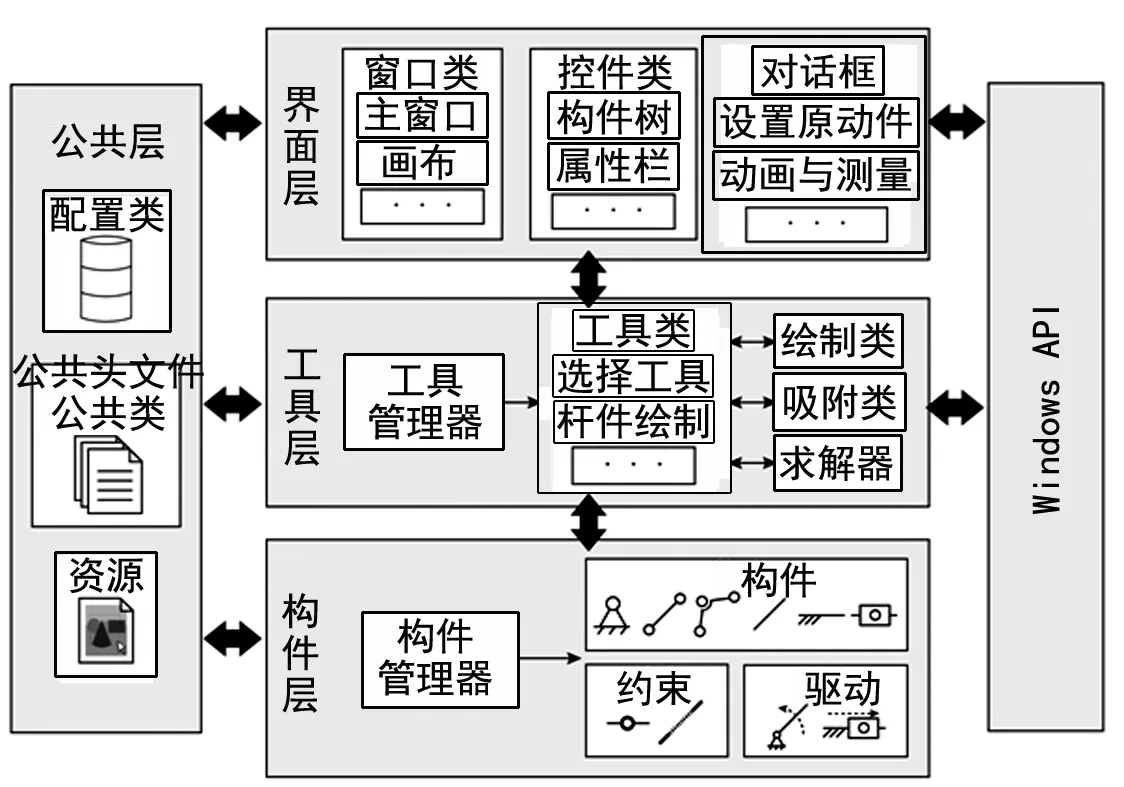
图4 程序结构组成
界面层负责程序的界面显示,各个控件的业务逻辑,弹出对话框。工具层包含工具库,绘制类,吸附类和求解器:工具库包含实现各类构件绘制的工具类;绘制类提供各类构件及矢量图形的绘制函数;吸附类用于在构件绘制时提供吸附功能;求解器如前文所述,用于求解运动学约束方程。构件层将各类构件、约束及驱动封装为类,构件管理器用于管理构件信息,输入输出构件数据文件。公共层包含配置类、公共函数库及资源,配置类存储程序当前的单位、比例、坐标原点、线型、颜色等信息,供其他层调用。
界面层与工具层在实现逻辑上通过直接调用Windows API实现,不依赖JRE、.net Framework等框架及MFC、Qt等类库。
3.2 求解算法及动画逻辑
构建完成机构系统后,拖动构件、点击刷新、运行仿真都将激活求解器。求解时,程序对构件、约束及驱动进行遍历,生成约束方程及驱动方程。此时得到整个机构的方程组,之后将机构的当前位置作为求解器中各未知量的初值,代入求解器进行求解。若求解成功,则将求解器中各未知量数据传回杆件,刷新画布显示结果。程序支持动画功能。将时间参数连续传入求解器并存储求解结果,将求解结果连续送入画布绘制机构,即可实现动画效果。
4 应用实例
牛头刨床六杆机构如图5所示。

图5 牛头刨床六杆机构运动简图
各构件尺寸为l1=125 mm,l3=600 mm,l4=150 mm,主动件为构件1,以ω1=360 (°)/s等速转动,初始位置为φ1=0 (°),l5为从动件,求E点处x方向的位移、速度及加速度。
建模及分析过程如下。首先在图6所示程序主界面上点选工具,在操作区绘制各构件,绘制过程中将自动产生捕捉,并建立起约束关系,操作方式类似于AutoCAD。
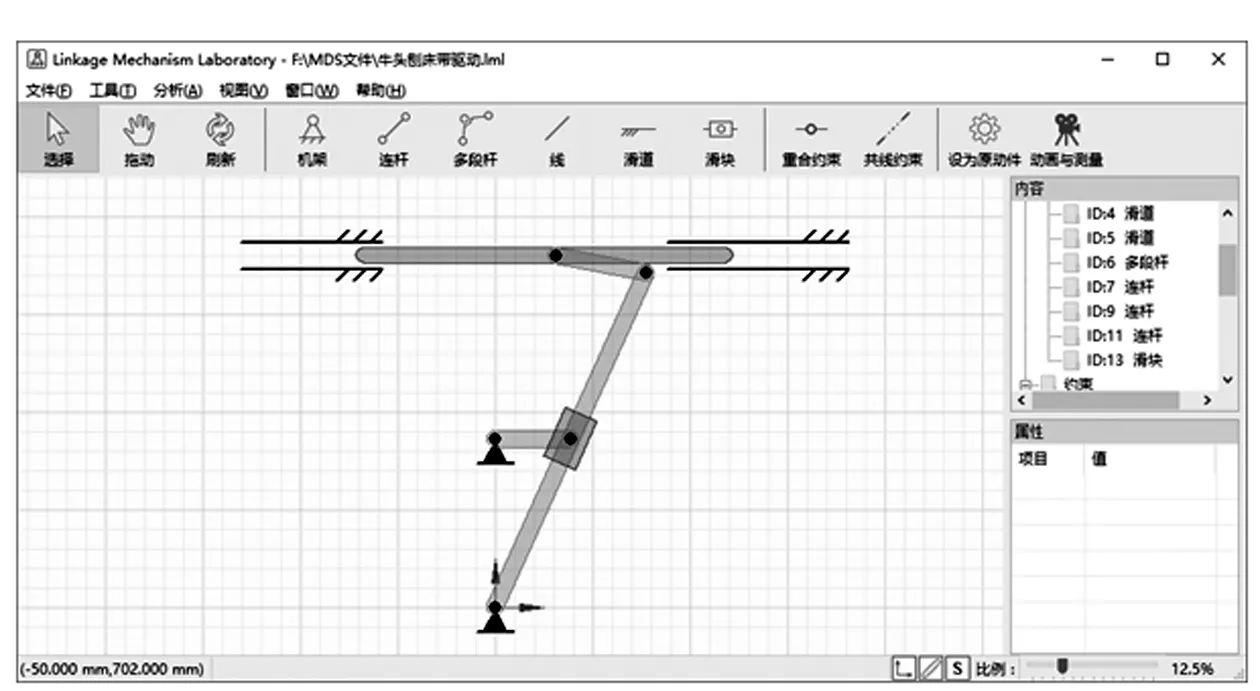
图6 程序界面
之后使用选择工具选中连杆1,点击工具栏上“设为原动件”按钮,弹出如图7所示窗口,设置原动件运动规律。此时机构建立完毕。

图7 设置原动件界面
点击主界面工具栏上“动画与测量”按钮,弹出窗口如图8所示。设置好各测量项目,点击“开始分析”按钮,程序将对机构在指定时间内的运动进行分析。分析完成后,将弹出测量结果线图,即E点在x方向的位移、速度及加速度,如图9所示。点击线图窗口菜单项可将线图保存为图片及csv数据文件。在“动画与测量”界面上拖动时间轴或者点击播放等按钮可以查看机构运动仿真动画,如图10。

图8 动画与测量界面

图9 LML输出位移、速度、加速度线图
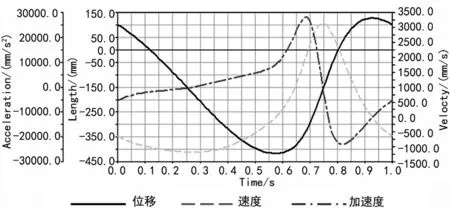
图10 ADAMS输出位移、速度、加速度线图
表1为本文程序LML进行位移、速度、加速度分析的数据与ADMAS的对比。从线图及输出数据来看,牛头刨床推程运动速度平稳,加速度小;回程速度变化大,加速度大,符合急回运动特性,验证了程序求解的正确性。
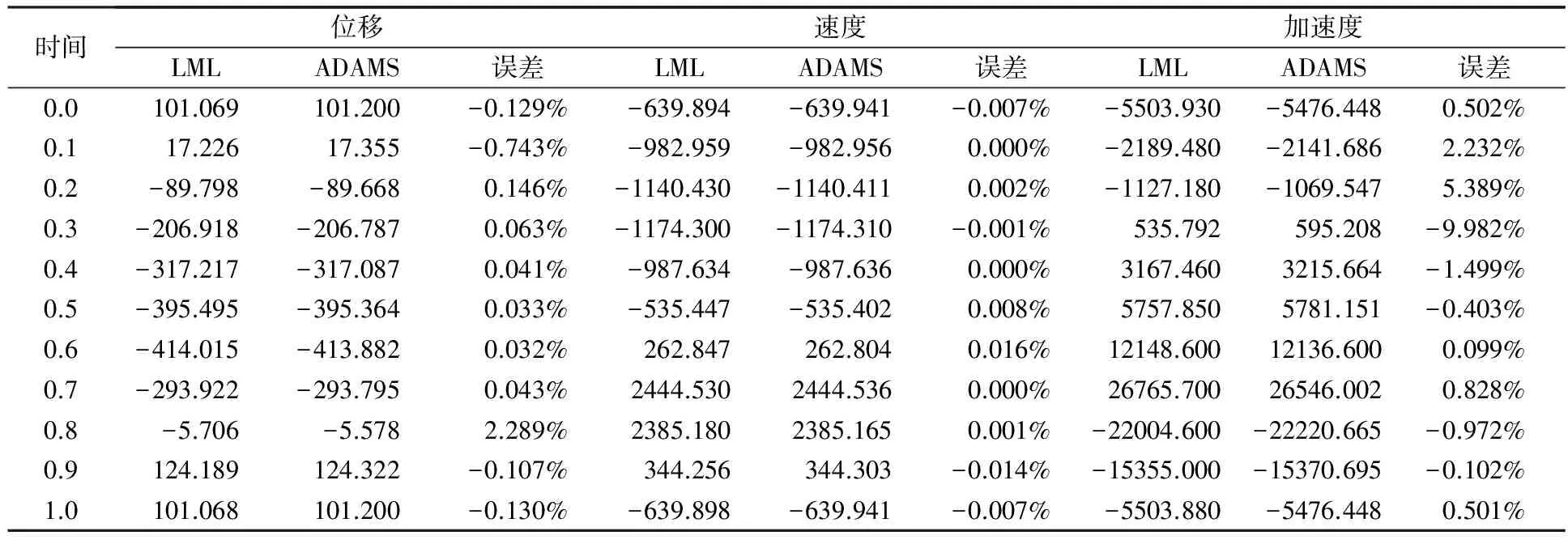
表1 位移、速度、加速度分析数据与ADAMS对比
5 结 论
建立了基于约束的平面连杆机构系统运动学模型,通过表达式树实现基于牛顿—拉夫森迭代法的通用非线性方程组求解器,开发了平面连杆机构仿真程序。
(1) 封装了Windows基本窗口及原生控件,内部功能完全通过Windows API实现,程序平台依赖性低,体积小,可在没有安装任何运行库的Windows XP以上系统运行。封装的窗口类及控件类可作为独立类库用于开发Win32界面程序。
(2) 求解器核心基于C++面向对象编程方法设计,可作为通用的线性、非线性及不定方程组解算工具。求解器不依赖杆组理论,可求解任意杆组级别、多自由度机构的运动学约束方程。
(3) 围绕平面连杆机构的设计、编辑、分析、动画功能设计了简明的用户操作界面及人机交互方式,实现真正的“拖拽式编辑”,程序自动吸附节点、添加约束,用户不需要介入节点编号等繁琐细节,所有操作所见即所得,并可拖动机构构件查看任意运行位置,原动件可设置任意表达式的运动规律,输出位移、速度、加速度图像及数据。与ADAMS的仿真结果对比验证了求解的正确性。
[1] 李永旭,刘 钊,李小江.平面连杆机构计算机建模与通用分析软件的开发[J].机械设计,2006,23(5): 58-60.
[2] 田 松.基于杆组理论的III级机构运动分析与仿真[D].武汉:武汉科技大学,2007.
[3] 李小江.MAD中的RRR杆组原理及应用[J].机械设计与制造,2008(3):66-68.
[4] 黄 河.平面连杆机构通用分析程序的研究与开发[D].西安: 长安大学,2008.
[5] 岳一领,陆凤仪,张志鸿.连杆机构设计仿真平台在机械原理教学中的应用[J].太原理工大学学报(社会科学版),2009,27(1):74-76, 88.
[6] 王炎欢.机构仿真软件的研究与开发[D].合肥:合肥工业大学,2006.
[7] 徐春雷,潘宏侠,李 冉,等.基于Matlab的平面连杆机构仿真软件的研究[J].机械设计与制造,2012,12(12):94-96.
[8] Haug Edward J. Computer aided kinematics and dynamics of mechanical systems:Basic methods Vol.1[M].Boston:Allyn and Bacon, 1989.
[9] Charles Petzold. Programming Windows: 5thed.[M]. Redmond: Microsoft Press,1998.
[10] Stanley B. Lippman, Josée Lajoie, Barbara E. Moo. C++ Primer: 5thed[M].Boston: Addison-Wesley Professional, 2012.
[11] Weifeng Huang. Automated synthesis of planar mechanisms with revolute, prismatic and pin-in-slot joints[D]. United States: Oregon State University, 2015.
[12] Feng Yuan. Windows graphics programming: Win32 GDI and DirectDraw[M].New Jersey: Prentice Hall, 2000.
[13] 李正彪,余 波.用矩阵的初等列变换求解多元线性不定方程[J].云南民族大学学报(自然科学版),2006,15(2):102-104.
[14] 李 超,阮 威,张 龙,等.计算机代数系统数学原理[M].北京:清华大学出版社,2010.
[15] 金一庆, 陈 越, 王冬梅.数值方法[M].第2版.北京:机械工业出版社,2015.

