借助差异 互帮互学——基于前测的“三位数乘两位数”教学实践与思考

◇谢玉娓 林俊峰

在班级授课制下，如何利用学生的学习差异帮助学生学习？本文以北师大版教材四年级上册第三单元“乘法”的第一课时“卫星运行时间（三位数乘两位数）”为例，谈谈点滴教学思考。

学习本课之前，学生对“三位数乘两位数”知道了些什么？差异化的教学先从了解学生差异开始。我们先对班上54个学生进行了学情前测，测试的题目是一个开放式的问题：想办法算出211×42的得数（无任何提示）。

前测情况统计如下表所示：

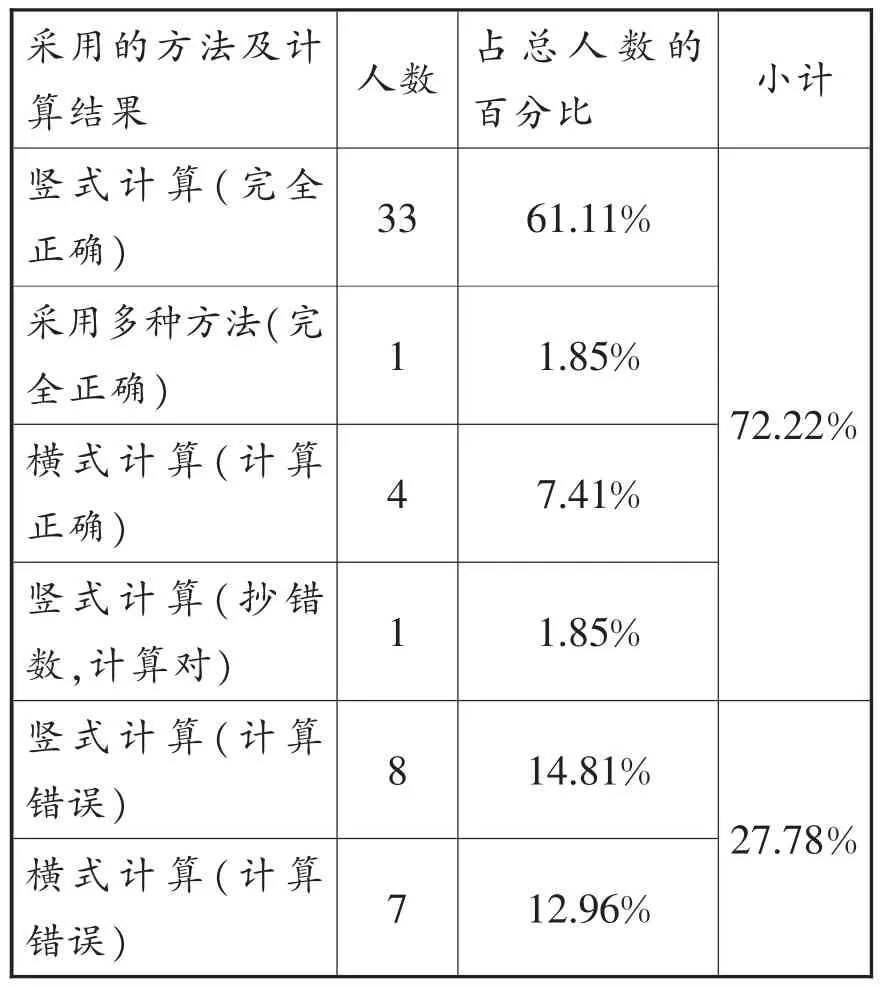
采用的方法及计算结果 人数 占总人数的百分比 小计竖式计算（完全正确） 33 61.11%72.22%采用多种方法（完全正确） 1 1.85%横式计算（计算正确） 4 7.41%竖式计算（抄错数，计算对） 1 1.85%竖式计算（计算错误） 8 14.81%27.78%横式计算（计算错误） 7 12.96%

计算正确的学生中，有采取不同的方法；计算错误的学生中，也存在不同的错误原因。分析错误原因如下：用竖式计算出错的8个学生里，其中1个学生将“211×42”误算成“211×44”、5个学生在竖式第二层“211×40”计算时出错、2个学生在竖式第一层“211×2”计算时就已出错；而采用横式计算的7个学生，都尝试将211或42拆分，转化成已学过的两、三位数乘一位数或两位数乘两位数，而后将乘积相加，但都在某一个环节出错。

基于这份前测，引发了我的思考：

1.学生在学习新数学知识之前，不是白纸一张，他们已有各种不同的理解。

2.若教学的方法和模式依旧“重复昨天的故事”，那么这超过70%的“不教已会”的学生在“陪学”中是否会逐渐失去学习数学的兴趣？

3.对于出错的27.78%的学生，他们的学习困惑是什么？如何采取针对性措施帮助他们学习？

4.面对这么大差异的教学现实，如何在课堂有效地施教，兼顾学生的多样性呢？

基于以上思考，我将本课的教学目标设定为：

（1）结合现实问题，利用学生学习差异互助学习，让不同能力的学生都能参与课堂，经历三位数乘两位数计算方法的探索过程，体会算法多样化，理解竖式计算的道理，能用竖式正确进行计算。

（2）在解决问题的过程中，让学生能选择合适的方法进行估算。

（3）在与他人交流算法的过程中，沟通新知和旧知间的联系，整体把握笔算乘法的内涵，提升学生的学习力。

具体来说，整个课堂的教学设计分以下几个环节：

一、唤醒——回忆旧知、揭示课题、任务驱动

师：以前，我们学习了有关乘法的哪些知识？

生：两位数乘两位数。

生：还有更早的两、三位数乘一位数。

师：猜猜今天我们要学习的内容可能是什么。

生：（齐）三位数乘两位数。

师：还真说对了！今天我们要学习的是三位数乘两位数。你们觉得三位数乘两位数会不会很难。

生：我觉得不会，因为我们已经学过了两位数乘两位数，我觉得它们的方法和道理应该是一样的。

师：既然大部分同学都摇头表示不难，那么，现在有两种方法供大家选择，方法1是老师讲你们听，方法2是同学们自己当小老师教会小伙伴。你们选择哪一种方法？

（学生选择方法2并跃跃欲试）

思考：在本课之前，学生经历了一个较长的“整数乘法计算”的过程，适时唤醒学生对所学知识的回忆，对即将进行的迁移学习显得尤为重要。而“听老师讲解”还是“自己当小老师”的选择，既尊重了学生，又让学生有了“任务驱动”，感受到“当小老师”的荣耀与责任，为课堂互助学习提供了更好的保障。

二、互学——同桌交流、外化思维、互帮互学

呈现教材“卫星运行时间”的情境图（如图1），引导学生获取数学信息后提出第一个任务：估一估，卫星绕地球21圈大概需要多长时间？与同伴交流你的想法。学生在交流中呈现了以下四种估算方法：100×20=2000（分）、114×20=2280（分）、110×20=2220（分）、120×20=2400（分），并一致认为卫星运行21圈的时间是2000多分钟，且会比2280分多。

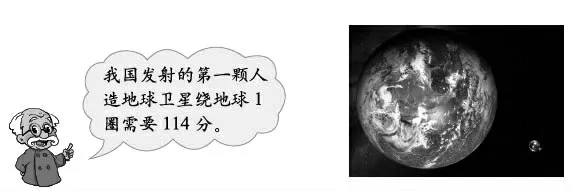
图1

在此基础上提出第二个问题：请算一算，绕地球21圈究竟需要多少时间？

（学生独立思考后尝试计算，教师巡视指导并收集学生资源）

师：大部分同学至少采用一种方法算出了结果，现在，请同桌互相交流：说一说你是怎么算的，讲清你这么算的道理。如果同伴的方法与你的不一样，请尽量读懂同伴的想法。

在巡视中，教师重点参与需要指导的小组，帮助学生外化思维，暴露困惑，在适当处给以点拨，促进同桌交流得以顺利进行。

思考：教师，要“有所为，有所不为”，且要分清“何时为，如何为”。尽量为学生提供安全的交流氛围，留出学习的空间与时间，让同伴间的对话更为有效。

三、共学——多维对话、纵横联通、整体把握

师：谁愿意来当小老师，向小伙伴们展示你的方法？

（生1上台板演。如图2）

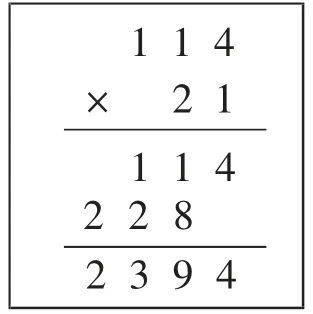
图2

师：谁读懂了他的方法？能不能说说每一层分别表示什么？

生2：第一层是114乘1得来的，表示114。第二层是114乘20得来的，表示2280。

师：第二层这里明明写着228，你怎么说是2280呢？

（这正是前测中学生出现错误的地方，是他们的学习难点，教学，就要抓“痛痒处”）

生：（齐）个位上省略了1个0。

生2：因为2在十位上，表示2个十。114乘20得到的是228个十，8在十位上，只不过个位上的0省略不写了，所以是2280。

生3：我补充一下，因为第二层的228，左边的第一个2是在千位上，所以是2280。

师：原来是这样呀（相机板书）。2394又是怎么来的呢？

生2：是114加2280的和。

师：（问生1）你觉得生2读懂你的方法了吗？

生1：他都说对了。

师：刚才生1是用竖式进行计算的，也是用竖式计算的请举手。除了用竖式计算，你还有不同的方法吗？

（生4上台板演。如图3）

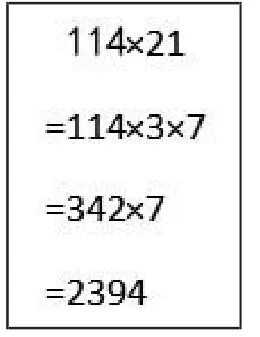
图3

师：你问问哪些同学读懂了你的方法，并请一个同学说一说。

生5：生4把21分成了3乘7，这样先算114乘3，然后再乘7。

师：明明是114乘21，为什么要把21分成3乘7呢？

生5：因为114乘21是三位数乘两位数，我们还没学。我们转化成了114乘3再乘7，就变成了我们学习过的三位数乘一位数，我们就会计算啦。

（教师相机板书：“未学”转化成“已学”）

生6：我的想法和生5差不多，但我和他的方法不太一样。（生6上台板演。如图4）我是先算20圈需要多少时间，再算1圈需要多少时间，最后算出一共需要多少时间。

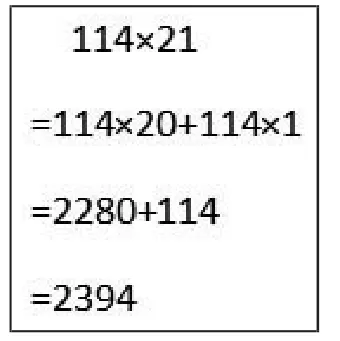
图4

生7：老师，我还有不一样的方法，我是用表格法算的（如图5）。

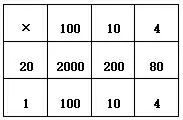
图5

师：你能向大家具体介绍你的方法吗？

生7：我把114分成100+10+4，把21分成20+1，这样，我就可以口算出每一部分的积，再把第一层的2280加上第二层的114等于2394。

师：为什么你要这样拆分呢？

生7：因为这样，都变成了我们以前学会的整十、整百数乘一位数和一位数乘一位数了，我们只要口算就能算出结果了。

师：现在黑板上有同学们想出的4种方法，你觉得这4种方法之间有什么相同的地方吗？你可以选择两种方法进行比较。

生8：我来说方法1和方法3之间的联系。你们看，方法3的114×20=2280，是方法1竖式计算的第二层，方法3的114×1=114，是方法1竖式计算的第一层，它们最后都是算2280+114=2394。我觉得这两种方法其实道理是一样的。

师：非常好，这两种方法其实是一样的，只不过这（方法1）是用竖式计算，而这（方法3）是用横式计算的。

生9：我还有新的发现。你们看，方法4（表格法）和方法1、方法3其实也是一样的（生9上台边说边连线。如图6）。

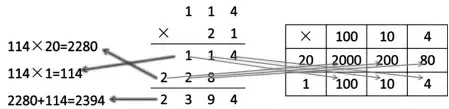
图6

师：通过刚才的比较，你们有什么发现？

生：黑板上这几种方法计算的道理其实都是一样的。

生10：我觉得三位数乘两位数和两位数乘两位数的方法和道理是一样的，只不过三位数比两位数多了百位上的数而已。

师：是的，三位数乘两位数和两位数乘两位数的算理和算法都是一样的，比如114×21，也是先用个位上的1去乘114得到几个一，再用十位上的2去乘114得到几个十，最后把乘得的积加起来。

思考：课堂上，我们可以看出学生已经能够自主把两位数乘两位数的算理和算法，迁移运用到三位数乘两位数上。学生当“小老师”讲算法和算理，生生间、师生间的互相倾听、交流、追问、辨析，使得本课的计算教学不仅仅是停留在表面的计算层次，而是深入比较、沟通新知与旧知间的联系，在“不同”中寻找“相同”，感悟计算的本质。

这样多维对话的“共学”，让前测中的72.22%“不教已会”的学生有了展示自我的舞台，而剩下的27.78%的学生在一次次的互帮互学中，获得了安全的心理环境，他们可以“慢下来”学习，逐渐跟上大部分学生学习的脚步。这样的“共学”，让课堂有了勃勃的生机，听得到思维拔节的声音。

在本课学习后的第二天，我对我班54个学生又进行了一次后测，要求是“用多种方法算出211×42的结果”。后测结果显示，只有1个学生在计算时出现了错误，其他53个学生至少能用一种方法正确计算，大部分学生能用多种方法计算出结果。这一结果，说明合理利用学生差异进行互帮互学是可行的。