基于K-SVD学习字典的机织物纹理表征及应用

吴 莹， 汪 军,2(.东华大学 纺织学院， 上海 20620； 2.东华大学 纺织面料技术教育部重点实验室， 上海 20620)

纹理是一种反映图像同质现象的视觉特征，它体现了物体表面的具有缓慢化或周期性变化的表面结构组织排列属性，如遥感卫星图像[1]、生物医用[2]。以及纺织品图像[3]等。作为基础研究的纹理分析在许多领域都有广泛的应用，如工业产品质量检测、医学图像分析、遥感图像分析等。在纺织领域，纹理分析在织物图像的描述、重构、分类以及疵点自动识别检测中都具有重要的作用。机织物是由经纬纱按照一定规律垂直交织而成的，其纹理具有一定的周期性、方向性和结构特性，但是由于机织物参数如纤维原料、纱线支数、经纬密度、组织结构等复杂多变，最终导致机织物纹理千变万化[3]。为了实现机织物表面纹理的在线检测，因此，如何有效地表征机织物纹理是非常有必要的。

目前有关织物纹理分析的研究较少，研究热点是其应用领域的探究与分析，如织物瑕疵检测[4-6]，织物组织结构自动识别[7-8]，织物密度的自动识别[9]等。而基于传统纹理分析的检测织物瑕疵方法[10-12]大都存在通用性差的问题，这是因为训练参数过多，特征不灵活，所以工业实时在线检测仍是一个挑战[13]。为了获得灵活的织物纹理特征，研究人员提出了基于学习训练的方法来描述纹理特性。Zhou等[14]提出稀疏字典重构的方法来自动识别织物疵点，该方法能较好地适应织物纹理。Zhu等[15]采用小尺度过完备字典可以有效地检测斜纹、平纹、条纹织物等的瑕疵点。很少有研究者将稀疏表示算法用于机织物纹理分析研究上，因此，本文提出一种基于训练字典的机织物纹理分析的方法。

1 机织物纹理的稀疏表示原理

任意给定织物纹理图像，其灰度矩阵Y=[y1,y2,…,yn]，yi∈Rm，在l2范数近似条件下，图像稀疏表示构造的优化函数如下：

(1)

式中：T为正整数，控制系数矩阵的基数即稀疏度；‖αi‖0表示系数矩阵中的非零元素个数。由于式(1)中的D和α都是未知的，求解问题的精确解是1个NP-hard 问题，典型的做法就是求解近似解。此时，稀疏表示包括2部分：字典更新和稀疏编码。稀疏编码直接采用OMP(orthogonal matching pursuit)算法来求解稀疏系数，因其简洁有效。本文着重讨论字典更新准则，即字典设计。

在稀疏表示前，需要先给定初始字典，之后再用给定的字典求解稀疏系数。字典的类型有2种：预构的字典和学习字典[16]。预先定义的字典一般是由数学变换得到的，如轮廓波(contourlet)[17]、条带波(bandelet)[18]、离散余弦变换(DCT)[19]，这类字典计算的速度很快，但其稀疏化能力局限于所设计的信号。此外，该类字典的自适应性较差，为了突破这些限制，Aharon等[20]提出了K-SVD字典。K-SVD字典不仅可有效减少字典中的原子数目，而且训练后的字典还可有效地表示初始字典的信息。为使得字典能更好地适应织物纹理，本文采用K-SVD 字典学习来更新字典。考虑到如果每幅织物图像都单独学习的计算量大[21]，选取三原组织的纹理图像来训练字典，这样既有预购字典的优势，也可更好地适应织物纹理。设计训练首先从不同的织物图像中提取超过 1 000 个8像素×8像素大小的图像块，并用K-SVD 离线训练得到一个字典个数为256的字典，且每个字典的维数为64。

具体的训练流程如下。

首先给定初始字典D=[d1,d2,…,dk]，di∈Rm，优化问题式(1)变成寻找样本集yi的稀疏表示αi的问题，即稀疏编码阶段，可采用OMP 算法近似求解，即

约束条件‖αi‖0≤T

(2)

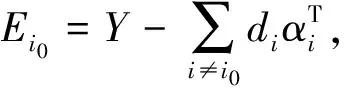
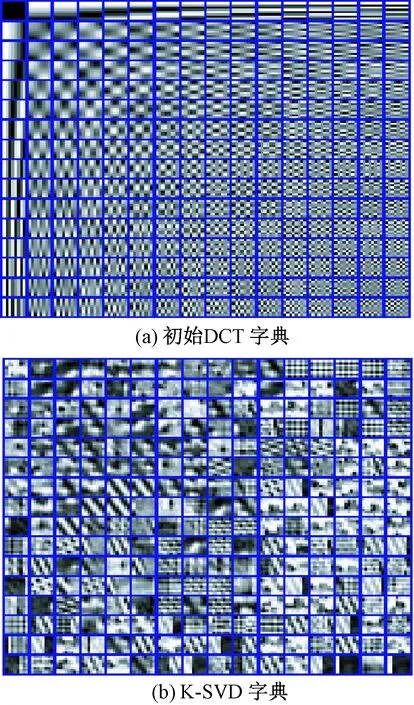
图1 不同类型的字典Fig.1 Different kinds of dictionaries. (a) Initial DCT dictionary; (b) Trained dictionary

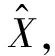
(3)

(4)

(5)

(6)

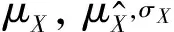
S的取值范围为[-1, 1]。S值越接近1，表明融合图像与原图像的亮度、对比度和结构越相似，重构图像的质量越好。

2 稀疏基数T的优选

在织物样本图像稀疏表示之前，需要确定稀疏度(基数)T，因为其直接关系到检测结果的好坏。例如：当稀疏度过小时，虽然计算速度快，但是不能很好地重构机织物纹理；当稀疏度过大时，计算负担会大大增加。结合本文算法的2种应用，即重构图像和织物瑕疵检测，本文选取稀疏度T=[2,3,…,15]，研究了T(2～15之间所有的整数共14个)对织物纹理表征的影响。选取平纹和蜂巢作为样本图像，重构结果见图2。重构图像质量随着稀疏基数的增大而变好，即P值逐渐增大，S也是逐渐增大。当T<6时，不论P还是S的增长速率都较快；当T>6时，S值也趋于稳定，P值也是缓慢增加。虽然织物样本的结构参数不同，但是随着T的增大，运行程序所需的时间都是逐渐增加。当T=6时，样本图像的P值大于30 dB，S大于0.9，程序运行大约为110 s，因此，选择稀疏基数T=6 来重构机织物纹理图像。瑕疵检测对于样本图像的重构效果要稍弱， 当T=4时，S约为0.86，能较好地自动识别瑕疵区域。

图2 不同稀疏基数的重构结果Fig.2 Reconstructed results with different values of sparsity T. (a) P value; (b) S value; (c) Running time

3 实验结果与讨论

为了验证算法的有效性，本文选取了不同材质、组织的织物作为样本图像，并与初始DCT字典的重构效果作了对比。样本是8位灰度图像，样本尺寸为256像素×256 像素。

3.1 机织物纹理的稀疏表示

平纹(p)、斜纹(t)、缎纹(s)、蜂巢(h)，DCT重构得到的样本图像平纹(p1)、斜纹(t1)、缎纹(s1)、蜂巢(h1)以及K-SVD字典的重构样本平纹(p2)、斜纹(t2)、缎纹(s2)、蜂巢(h2)，视觉表征结果见图3，量化的测试结果见表1。从视觉角度来讲，2种算法的表征结果很难区分。对于平纹和缎纹组织，K-SVD字典的效果要好于DCT 字典约1 dB；蜂巢和斜纹的重构效果改进较少。这是因为训练样本织物组织图像，学习后得到的字典能有效包括样本的纹理特征，所以能更好地适应织物图像。

图3 测试样本的表征结果Fig.3 Representation results of test samples

表1 2种方法的测试结果Tab.1 Test results with two different methods

3.2 织物瑕疵检测

为更好地验证算法的有效性，将K-SVD训练字典重构的样本图像用于疵点的自动检测。先将织物图像转换为灰度矩阵后与重构图像作差；其次是求出残差矩阵每列的最小平方误差，正态分布的95%置信区间确定阈值；最后，大于阈值的部分设定为瑕疵区域，小于阈值的为正常纹理。选取断疵、缺纬拖纱2种疵点样本，采用不同方法得到的检测结果见图4。由图可知：断疵的疵点，DCT字典漏检了部分瑕疵区域；缺纬拖纱的疵点，DCT字典误检了部分正常纹理为瑕疵区域；而K-SVD学习字典拥有织物纹理的特征，因此它能更好地适应织物瑕疵，进而完整地检测出瑕疵区域，有效降低了误检率和漏检率。总之，本文算法K-SVD 字典的检测效果要好于初始DCT字典。

图4 瑕疵异常图及检测结果Fig.4 Fabric defects image and detection results.(a) Original image with broken defect; (b) Detection result of DCT dictionary of (a); (c) Detection of result of K-SVD dictionary of (a); (d) Original image with mispick and flying threads;(e) Detection result of DCT dictionary of (d); (f) Detection result of K-SVD dictionary of (d)

4 结 论

基于K-SVD学习字典的自适应性，本文直接选取三原组织(平纹、斜纹和缎纹)作为训练样本，最终通过K-SVD方法训练得到一个过完备字典。首先，探讨了不同稀疏基数对织物图像重构的影响，结合程序运行时间，最终选择T=6用于正常纹理图像的重构，T=4 用于织物的疵点检测。其次，利用该字典用于机织物纹理表征，重构了正常的机织物纹理图像。实验结果表明，本文算法不仅能近似重构织物样本图像，而且相比DCT 字典重构的图像质量更好。在此基础上，采用阈值法检测织物瑕疵，DCT 字典不仅会漏检部分主要断疵的区域，而且还将部分正常的纹理区域误检为瑕疵。而训练字典由于包括三原组织的主要纹理特征，其鉴别能力明显优于DCT 字典。

FZXB

[1] 李龙燕, 胡福乔. 基于Gabor小波滤波器的遥感图像多频道纹理分析[J]. 计算机工程, 2003, 29(20): 127-129.

LI Longyan, HU Fuqiao. Remote-sensing image multichannel textural analysis based on 2-D Gabor filters[J]. Computer Engineering, 2003, 29(20): 127-129.

[2] 刘昉, 程敬之. 分形模型的超声图像纹理分析 [J]. 生物医学工程学杂志, 1999(3): 329-332.

LIU Fang, CHENG Jingzhi. Texture analysis of B-Scan image using fractral dimension[J]. Jounral of Biomedical Engineering, 1999(3): 329-332.

[3] 薛乐, 李立轻, 汪军. 应用频谱图的机织物纹理分析[J]. 纺织学报, 2015, 36(7): 55-60.

XUE Le, LI Liqing, WANG Jun. Study on woven fabric tetxure using spectrum[J]. Jounrnal of Textile Research, 2015, 36(7): 55-60.

[4] LIU J L, ZUO B Q. The Recognition of fabric defects using wavelet texture analysis and LVQ neural net-work [C]//International Congress on Image and Signal Processing. New York: IEEE, 2009: 1-5.

[5] NGAN H Y T, PANG G K H, YUNG N H C. Automated fabric defect detection-a review [J]. Image and Vision Computing, 2011, 29(7): 442-458.

[6] QU T, ZOU L, ZHANG Q L, et al. Defect detection on the fabric with complex texture via dual-scale over-complete dictionary [J]. Journal of the Textile Institute, 2016, 107(6): 743-756.

[7] SABUNCU M, OZDEMIR H. Recognition of fabric weave patterns using optical coherence tomo-graphy [J]. Journal of the Textile Institute, 2016, 107(11): 1406-1411.

[8] HUANG C C, LIU S C, YU W H. Woven fabric analysis by image processing: part I: identification of weave patterns[J]. Textile Research Journal, 2000, 70(6): 481-485.

[9] TECHNIKOVA L, TUNAK M. Weaving density evaluation with the aid of image analysis [J]. Fibres & Textiles in Eastern Europe, 2013, 2(98): 74-79.

[10] LI P, ZHANG H, JING J, et al. Fabric defect detection based on multi-scale wavelet transform and Gaussian mixture model method [J]. Journal of the Textile Institute, 2014, 106(6): 1-6.

[11] 王钢, 周建, 汪军,等. 采用奇异值分解的机织物瑕疵检测算法 [J]. 纺织学报, 2014, 35(7): 61-66.

WANG Gang, ZHOU Jian, WANG Jun, et al. Woven fabric defect detection using singular value decomposition [J]. Journal of Textile Research, 2014, 35(7): 61-66.

[12] 田承泰, 步红刚, 汪军, 等. 基于时间序列分形特征的织物瑕疵检测 [J]. 纺织学报, 2010, 31(5): 44-47.

TIAN Chengtai, BU Honggang, WANG Jun, et al. Fabric defect detection based on fractal feature of time series [J]. Journal of Textile Research, 2010, 31(5): 44-47.

[13] 朱秋平. 基于稀疏编码的织物瑕疵检测算法研究 [D]. 武汉：武汉大学, 2014:1-5.

ZHU Qiuping .Research on fabric defect detection via sparse coding[D]. Wuhan: Wuhan University, 2014:1-5.

[14] ZHOU J, SEMENOVICH D, SOWWMYA A, et al. Sparse dictionary reconstruction for textile defect detection [C]//International Conference on Machine Learning and Applications. Washington: IEEE, 2012: 21-26.

[15] ZHU Q, WU M, LI J, et al. Fabric defect detection via small scale over-complete basis set [J]. Textile Research Journal, 2014, 84(15): 1634-1649.

[16] ELAD M, AHARON M. Image denoising via sparse and redundant representations over learned Dictionaries [J]. IEEE Transactions on Image processing, 2006, 15(12): 3736-3745.

[17] DO M N, VETTERLI M. The contourlet transform: an efficient directional multiresolution image represent-ation [J]. IEEE Transactions on Image Processing, 2005, 14(12): 2091-2106.

[18] LE P E, MALLAT S. Sparse geometric image representations with bandelets [J]. IEEE Transactions on Image Processing, 2005, 14(4): 423-438.

[19] WANG Y H, SHI M J, YOU S, et al. DCT inspired feature transform for image retrieval and recon-struction [J]. IEEE Transactions on Image Processing, 2016, 25(9): 4406-4420.

[20] AHARON M, ELAD M, BRUCKSTEIN A. K-SVD: an algorithm for designing overcomplete dictionaries for sparse representation [J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322.

[21] ELAD M. Sparse and Redundant Representations from Theory to Applications in Signal and Image Pro-cessing [M]. New York: Springer, 2010: 227-244.